Умножение комплексных чисел тригонометрической форме
Комплексные равенства (Сформулируйте смысл комплексного равенства)
1) 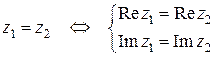 ;
;
2)  .
.
Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.
Примеры
1) 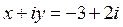
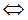
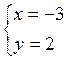 ;
;
2) 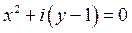
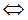
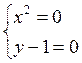
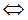
 .
.
Геометрическое изображение комплексных чисел (В чём состоит геометрическое изображение комплексных чисел?)
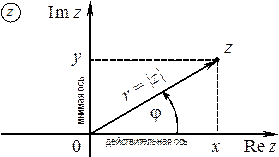
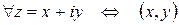
Комплексное число z изображается точкой (x, y) на комплексной плоскости или радиус-вектором этой точки.
 Знак z во второй четверти означает, что система декартовых координат
Знак z во второй четверти означает, что система декартовых координат 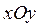 будет использоваться как комплексная плоскость.
будет использоваться как комплексная плоскость.
Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа?)
Модулем комплексного числа 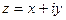 называется неотрицательное действительное число
называется неотрицательное действительное число
 .(2)
.(2)
Геометрически модуль комплексного числа — это длина вектора, изображающего число z, или полярный радиус точки (x, y).
Аргумент комплексного числа z— это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x, y)).
Обозначение  , причем
, причем  , или
, или 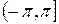 .
.
Для вычисления аргумента комплексного числа используется формула
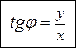 Аргумент комплексного числа ,(3)
Аргумент комплексного числа ,(3)
причем, при определении угла  по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z:
по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z:
|
|
|

Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа?)
Так как геометрически очевидно, что  и
и  , то
, то
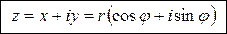 Тригонометрическая форма комплексного числа .(4)
Тригонометрическая форма комплексного числа .(4)
Запись z = x + iy называется алгебраической формой комплексного числа z; запись z = r(cosj + i sinj) называется тригонометрической формой комплексного числа z.
Примеры
Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.
1)z = 1 + i Þ
 ,
,
 Þ
Þ 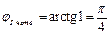
Þ 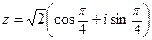 ;
;
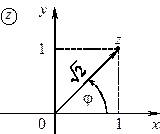
2) 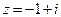 Þ
Þ
 ,
,
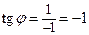 Þ
Þ 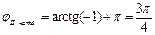
Þ  ;
;
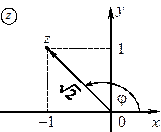
3) 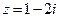 Þ
Þ
 ,
,
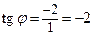 Þ
Þ
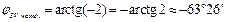 Þ
Þ
 ;
;

4) 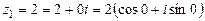 ,
,
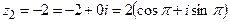 ;
;
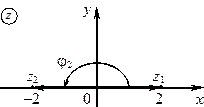
5)  ,
,
 ;
;

6)  ,
,
то есть для z = 0 будет
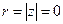 , j не определен.
, j не определен.
Арифметические действия над комплексными числами (Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.)
Сложение (вычитание) комплексных чисел
z1 ± z2 = (x1 + iy1) ± (x2 + iy2) = (x1 ± x2) + i(y1 ± y2),(5)
то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.
Примеры
1)(1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i;
2)(1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i.
|
|
|
Основные свойства сложения
1)z1 + z2 = z2 + z1;
2)z1 + z2 + z3 = (z1 + z2) + z3 = z1 + (z2 + z3);
3)z1 – z2 = z1 + (– z2);
4)z + (–z) = 0;
5) 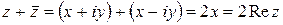 .
.
Умножение комплексных чисел в алгебраической форме
z1∙z2 = (x1 + iy1)∙(x2 + iy2) = x1x2 + x1iy2 + iy1x2 + i2y1y2 = (6)
= (x1x2 – y1y2) + i(x1y2 + y1x2),
то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой  и приведением подобных по действительным и мнимым слагаемым.
и приведением подобных по действительным и мнимым слагаемым.
Примеры
1)(1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i2 = 2 – 3i + 2i + 3 = 5 – i;
2)(1 + 4i)∙(1 – 4i) = 1 – 42 i2 = 1 + 16 = 17;
3)(2 + i)2 = 22 + 4i + i2 = 3 + 4i.
Умножение комплексных чисел тригонометрической форме
z1∙z2 = r1(cosj1 + isinj1)×r2(cosj2 + isinj2) =
= r1r2(cosj1cosj2 + icosj1sinj2 + isinj1cosj2 + i2 sinj1sinj2) =
= r1r2((cosj1cosj2 – sinj1sinj2) + i(cosj1sinj2 + sinj1cosj2))
Þ 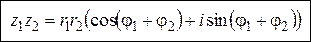
Произведение комплексных чисел в тригонометрической форме , то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
Пример
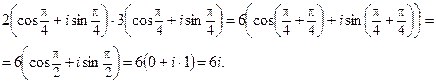
Основные свойства умножения
1)z1×z2 = z2×z1 — коммутативность;
2)z1×z2×z3 = (z1×z2)×z3 = z1×(z2×z3) — ассоциативность;
3)z1×(z2 + z3) = z1×z2 + z1×z3 — дистрибутивность относительно сложения;
4)z×0 = 0; z×1 = z;
|
|
|
5) 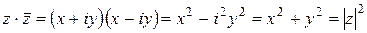 .
.
Деление комплексных чисел
Деление — это обратная умножению операция, поэтому
если z×z2 = z1 и z2 ¹ 0, то 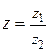 .
.
При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:
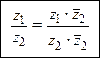 Деление комплексных чисел в алгебраической форме .(7)
Деление комплексных чисел в алгебраической форме .(7)
При выполнении деления в тригонометрической форме модули делятся, а аргументы вычитаются:
 Деление комплексных чисел в тригонометрической форме .(8)
Деление комплексных чисел в тригонометрической форме .(8)
Примеры
1) 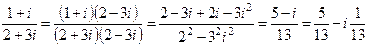 ;
;
2)  .
.
Дата добавления: 2021-03-18; просмотров: 66; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
