Свойства средней арифметической

Тема 5: Средние величины и показатели вариации

Вопросы: 5.1.Общие принципы применения средних величин. ( Виды средних)

Степенные средние.

5.3 Структурные средние.

Общие принципы применения средних величин

Средние величины - это величины, которые позволяют охарактеризовать явление по количественно варьирующему признаку.

Общие принципы применения средних величин.

1. При определении средней величины в каждом конкретном
случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные.

2. Средняя величина должна, прежде всего, рассчитываться
по однородной совокупности. Качественно однородные
совокупности позволяет получить метод группировок, который
всегда предполагает расчет системы обобщающих показателей.

3. Общие средние должны подкрепляться групповыми
средними.

Средние величины существуют в различных видах и формах. Выбор вида и формы средней зависит от вида осредняемого признака и наличия исходных данных.

Степенные средние

Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.

Выбор формы средней зависит от того, в каком виде представлены данные:

‒ если они сгруппированы, т.е. одно и то же значение признака встречается несколько раз, используются взвешенные средние;

‒ если каждое значение признака встречается только один раз, средняя рассчитывается в простой форме.

Выбор вида средней зависит от вида осредняемого признака и от наличия исходных данных.

В.Е.Овсиенко формализовал порядок выбора формы средней качественного признака на основе следующих правил:

1. Если имеется ряд данных по двум взаимосвязанным
показателям, для одного из которых нужно вычислить среднюю
величину, и при этом известны численные значения знаменателя
ее логической формулы, а значения числителя не известны, но
могут быть найдены как произведения этих показателей, то
средняя должная вычисляться по формуле средней арифме тической взвешенной.

2. Если в указанной постановке задачи известны численные
значения числителя логической формулы, а значения знаменателя
не известны, но могут быть найдены как частное от деления одного
показателя на другой, то средняя вычисляется по формуле
средней гармонической,

3. В том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле.

Таблица 1- Виды и формы средних величин

Вид степенной средней

Показатель степени, m

Формула расчета

простая

взвешенная

1. Общий вид

2. Гармоническая

-1

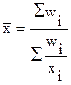
3. Геометрическая

→ 0

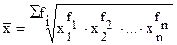
4. Арифметическая

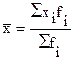
5. Квадратическая

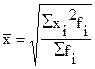
6. Кубическая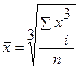

где - среднее значение признака;

х_i- индивидуальные значения осредняемого признака;

n - количество единиц совокупности;

f_i - частота (вес) индивидуальных значений осредняемого признака;

w_i = x_if_i - произведение индивидуального значения признака и его частоты.

Главное требование к формуле расчета среднего значения:

- все этапы расчета имели реальное содержательное обоснование;

- полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей.

Свойства средней арифметической

Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет.

1. Произведение средней ( ) на сумму частот (∑f) равно сумме произведения отдельных вариантов на соответствующие им частоты (∑хf) (расхождения – за счет округлений):

∑f = ∑хf (5.1)

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

(5.2)

3. Если все осредняемые варианты уменьшить или увеличить на постоянное число А , то средняя арифметическая соответственно уменьшиться или увеличиться на ту же величину:

(5.3)

4. Если все индивидуальные значения признака (т. е. все
варианты) увеличить либо уменьшить в одно и то же число раз
(или на одно и то же число), то среднее значение получившегося
нового признака будет во столько же раз (или на столько же)
отличаться от среднего значения исходного показателя

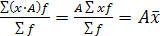(5.4)

5. Величина средней арифметической не изменится, если
веса всех вариантов умножить или разделить на одно и то же
число

(5.5)

Структурные средние

Помимо средних величин, в статистическом анализе используются и структурные средние: мода и медиана.

Мода - это значение признака, которое чаще всего встречается в ряде распределения.

В дискретных рядах модой является значение признака в той группе, у которой наблюдается наибольшая частота. Определить моду в этом случае можно визуально.

В интервальных рядах распределения мода также находится в той группе, у которой наибольшая частота. Но так как в интервальных рядах признак может принимать любое значение в заданном интервале, точное значение моды следует определять по специальной формуле:

(10)

где х_мо - нижняя граница модального интервала;

i_мо - величина модального интервала;

f_мо- частота модального интервала;

f_(мо-1)- частота интервала, предшествующего модальному;

f_(мо+1)- частота интервала, следующего за модальным.

Модальным является интервал, имеющий наибольшую частоту!!!!!!!!!

Значение моды, рассчитанное по формуле, не может быть меньшим, чем нижняя граница модального интервала, и не будет превышать верхнюю границу модального интервала.

Медиана - это значение признака, стоящего в центре ранжированного ряда распределения.

В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – больше его.

Для ранжированного дискретного ряда с нечетным числом членов, медиана – варианта, расположенная в центре.

Для ранжированного дискретного ряда с четным числом членов, медиана равна средней арифметической из двух вариант, расположенных в центре.

В дискретном ранжированном ряду распределения медиана равна значению признака в той группе, у которой сумма накопленных частот равна или превышает половину суммы всех частот ряда распределения.

Сумма накопленных частот находится последовательным сложением частот каждой группы. Так, для первой группы сумма накопленных частот будет равна частоте этой группы, для второй группы - сумме частот первой и второй группы, для третьей группы - сумме частот первой, второй и третьей группы и т.д. накопленная частота последней группы будет равна общей сумме частот ряда распределения.

В интервальном ряде распределения медиана находится по специальной формуле:

(11)

где х_ме - нижняя граница медианного интервала;

i_ме- величина медианного интервала;

f_ме - частота медианного интервала;

Σf - сумма всех частот ряда распределения;

S_ме-1- сумма частот, накопленных до медианного интервала.

Медианным считается интервал, сумма накопленных частот которого равна или превышает половину всех частот ряда распределения!!!!!!!!!!

Значение медианы будет не меньше, чем значение нижней границы медианного интервала, и не превысит значения верхней границы медианного интервала.

По соотношению моды, медианы и средней можно судить о характере распределения признака. Распределение может быть симметричным. В этом случае наблюдается равенство между модой, медианой и средним значением признака (рис.5.1).

частота признака, (f_i)	у		М_о = М_е= .




		значение признака (х_i)

Рис. 5.1- Симметричный ряд распределения

Если между модой, медианой и средней выполняется соотношение (М_о< М_е< ), то мы имеем дело с правосторонней асимметрией. (рис. 5.2)

частота признака, (f_i)
	у





		значение признака (х_i)	х

Рис. 5.2- Ряд распределения с правосторонней асимметрией

При наличии левосторонней асимметрии мода, медиана и средняя связаны следующим образом:

частота признака, (f_i)	у		М_о > М_е >






		значение признака (х_i)		х

Рис. 3. Ряд распределения с левосторонней асимметрией

Определить наличие асимметрии можно и с помощью относительного показателя - коэффициента асимметрии. Он может быть рассчитан в двух вариантах - на основе моды или медианы.

, (5.8)

. (5.9)

Если A_s > 0, имеется правосторонняя асимметрия, если A_s < 0 - левосторонняя.

Дата добавления: 2021-03-18; просмотров: 68; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!