Понятие смежность и инцендентность.

    На рисунке голубым цветом отмечены две вершины, которые соединены ребром друг с другом. Такие вершины называют смежными.

 

 

    На рисунке красным цветом отмечены два ребра, которые идут в одну точку. Такие ребра как и вышеописанные вершины тоже называются смежными.

 

 

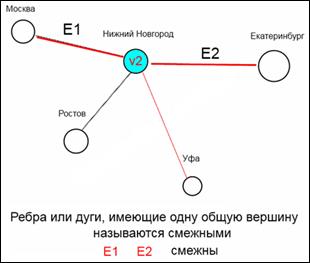
    Если объекты вершина и вершина однотипны, если объекты дорога и дорога однотипны, то объекты вершина и дорога не очень-то и однотипны, но чтобы обозначить связь вершины и дороги существует понятие инцендентности. Т.е. это принадлежность вершины графа к маршруту графа, если маршрут принадлежит вершине графа (стыкуется с ней), то маршрут и вершина инцендентны

 

 

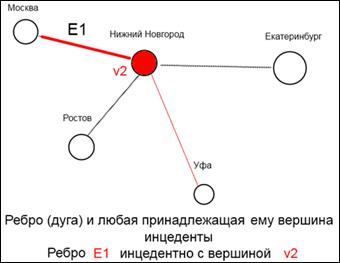
Изолированная вершина.

    Так как в графе может существовать такая вершина, к которой нет маршрутов, то для такой вершины существует понятие — изолированная вершина

 

 

 

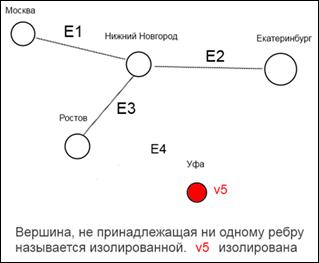
Нуль-граф.

    Этот рисунок уже был самым первым. Но для такой ситуации существует определение — нуль-граф

 

 

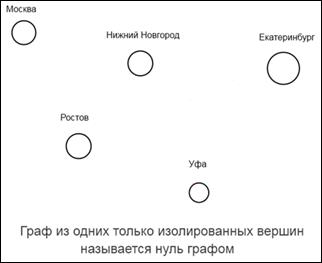
Полный граф.

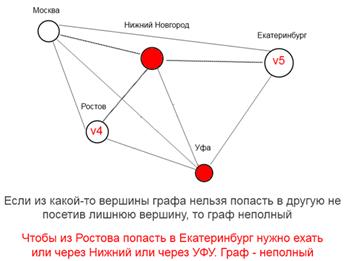
    Для решения некоторых задач и для изучения примеров нужно знать что такое полный граф. Полный граф — это такой граф, из любой вершины которого существует прямая связь с любой и с каждой другой вершиной этого графа

 

 

    Если для какой-то из вершин не существует прямого маршрут хотя бы в одну из других вершин графа, то такой граф неполный

 

 

 

    Пусть S – непустое конечное множество, V(2) – множество всех его двухэлементных подмножеств.

Определение 1.1.

    Псевдографом (или просто графом) G называется пара множеств (S,U), где U – произвольное подмножество множества V(2). При этом пишут G= (S,U).

Определение 1.2.

    Пусть G = (S,U) – псевдограф. Элементы множества S называются вершинами графа G, а элементы множества U – его ребрами.

Определение 1.3.

    Граф G = (S,U) называется пустым или нуль - графом, если U = ∅.

Определение 1.4.

    Число вершин графа G = (S,U) называется его порядком. Если порядок графа равен n, то пишут = n.

    Двухэлементное подмножество множества S(ребро), принадлежащее U и состоящее из элементов x и y будем обозначать через (x, y). В общем случае множество U может содержать пары с одинаковыми элементами вида (x, x) и одинаковые пары.

Определение 1.5.

    Ребра вида (x, x) называются петлями.

Определение 1.6.

    Одинаковые пары из множества U называются кратными (или параллельными) ребрами. Таким образом, псевдограф может содержать петли и кратные ребра. В этом смысле псевдографы еще называются графами с кратными ребрами и петлями.

Определение 1.7.

    Псевдограф без петель называется мультиграфом (или графом с кратными ребрами).

Определение 1.8.

    Мультиграф без кратных ребер называется простым графом. Таким образом, простой граф не содержит петель и кратных ребер. Графы имеют наглядную графическую интерпретацию в виде диаграмм, состоящих из точек и линий, соединяющих некоторые из этих точек. Точки соответствуют вершинам графа, а линии– его ребрам. При этом форма и длина линий значения не имеют. Важно лишь, что две данные точки соединены или не соединены линией.

Определение1.9.

    Граф называется неориентированным (кратко– неорграфом), если пары в множестве U являются неупорядоченными. Если (x, y) – неупорядоченная пара, то ребро (x, y) называется неориентированным, а вершины x и y называются концами неориентированного ребра (x, y).

Определение 1.10.

    Граф называется ориентированным (кратко – орграфом), если пары в множестве U являются упорядоченными.

Определение 1.11.

    Ребра орграфа называются дугами (или ориентированными ребрами). Вершина х дуги (x, y) называется ее началом, а вершина y – ее концом. В этом случае говорят, что дуга (x, y) исходит из вершины x и входит в вершину y. На диаграммах орграфов направления дуг отмечаются стрелками, которые примыкают к их концам.

Замечание 1.1.

    Неориентированное ребро (x, y) равносильно двум противоположно направленным дугам (x, y) и (y, x). Поэтому неориентированный граф можно рассматривать как ориентированный граф, который вместе с каждой дугой (x, y) содержит и дугу (y, x) противоположного направления.

    Условимся вершины графа обозначать буквами x, y, z (без индексов или с индексами), а ребра и дуги – буквами v, u, w (без индексов или с индексами).

    Рассмотрим ряд понятий и определений для неориентированных и ориентированных графов. При этом, если не будет оговорено особо, те же понятия и определения переносятся без изменений на неориентированные и ориентированные псевдографы.

Определение 1.12.

     Два ребра графа называются смежными, если они имеют общий конец.

Определение 1.13.

    Вершина х и ребро u графа называются инцидентными, если x является концом ребра u, и неинцидентными в противном случае.

Определение 1.14.

    Две вершины графа называются смежными, если существует инцидентное им ребро.

Определение 1.15.

    Число ребер (дуг) графа (орграфа) G, инцидентных данной вершине x_i называется степенью (валентностью) вершины x_i и обозначается через deg(х _i) (от англ. degree – степень).

    Вершина называется нечетной, если ее степень – нечетное число. Вершина называется четной, если ее степень число четное.

    Степень каждой вершины полного графа на единицу меньше числа его вершин.

 

 

Определение 1.16.

    Вершина графа называется изолированной, если ее степень равна нулю.

Определение 1.17.

    Вершина графа называется висячей, если ее степень равна единице.

Замечание 1.2.

    В случае неориентированного псевдографа обычно считается, что вклад каждой петли, инцидентной некоторой вершине x, в ее степень P(x) равен 2, в то время как вклад любого другого ребра, инцидентного вершине x равен 1.

Определение 1.18.

    Полустепенью исхода (захода) вершины x_i орграфа называется число deg ⁺ (xⁱ) (deg ^– (x_i)) его дуг, исходящих из вершины x_i (заходящих в вершину x_i). Для орграфа deg(x_i) = deg ⁺ (x_i) + deg ^– (x_i).

Замечание 1.3.

    В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине x, равен 1, как в deg ⁺ (x), так и в deg ^– (x).

Определение 1.19.

    Неориентированный простой граф, в котором любые две различные вершины смежны, называется полным. Полный граф порядка n обозначается через K_n.

Замечание 1.4.

     В полном графе каждая его вершина принадлежит одному и тому же числу ребер.

Определение 1.20.

    Неориентированный граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям.

Определение 1.21.

    Двудольный граф, любые две вершины которого, входящие в разные доли смежны,  называется полным двудольным. Полный двудольный граф, доли которого состоят из p и q вершин,  обозначается символом K_p,q.

 

 

Способы задания графов

1. Задать граф можно путем перечисления(списком)  дуг (или ребер) графа с указанием концов и добавлением списка изолированных вершин, например,граф с множеством вершин 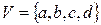 и списком дуг . 

 

 

2. Геометрическим способом. Граф может быть задан с помощью его диаграммы.

Пример. Построить графы:    а) Г = ,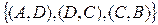 

                                          b) . Построение.

Один и тот же граф можно изобразить по-разному.

Примеры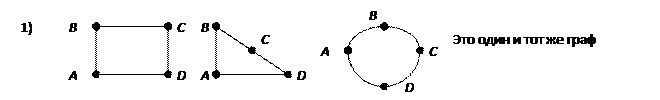

Замечание 2.1. Диаграмма графа наглядно иллюстрирует его свойства. Но не надо отождествлять эти понятия прежде всего потому, что одному и тому же графу можно поставить в соответствие внешне различные диаграммы.

3. Матричным способом.

Этот способ задания используется наиболее часто. Рассмотрим задание графа матрицей смежности вершин, матрицей смежности дуг, матрицей инциденций и матрицей Кирхгофа.

Определение 2.1.

    Матрицей смежности называется квадратная матрица 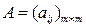, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент равен числу дуг, идущих из вершины x_i в вершину  x_j. Если исходящих дуг нет, то .

Определение 2.2.

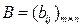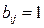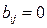    Матрицей инцидентности или инциденций называется прямоугольная матрица , строки которой соответствуют вершинам графа, а столбцы – ребрам. Если вершина x_i и ребро u_j инцидентны, то , и  в противном случае.

Пример. Составить матрицу смежности графа

 

Решение. Граф имеет 4вершины, следовательно, матрица смежности имеет размерность 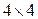. Наличие ребер: 1 в 1 – нет ребра, 1 в 2 – есть ребро, 1 в 3 – нет ребра, 1 в 4 – есть ребро. Следовательно, первая строка имеет вид: 0 1 0 1.

Вершина 2 соединена только с вершиной 1, следовательно, вторая строка имеет вид: 1 0 0 0. Вершина 3 – изолированная, следовательно, третья строка – нулевая. Вершина 4 соединена ребром с вершиной 1 и дугой с самой собой, следовательно, четвертая строка: 1 0 0 1.

 

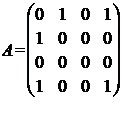
Тогда матрица смежности имеет вид: . 

 

 

Пример. Составить матрицу инциденции для графа.

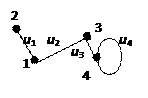
Решение. Обозначим ребра как u₁, u₂, u₃, u₄.

Матрица имеет вид: .

 

Изоморфные графы

Определение 3.1.

    Два геометрических графа называются изоморфными, если они являются диаграммами одного и того же графа (каждой паре вершин а, b графа G, соединенных ребром соответствует пара вершин 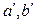графа так же соединенных ребром).

 

Взвешенные графы

Определение 4.1.

    Если каждой дуге (ребру) графа приписано неотрицательное число (вес), то он называется взвешенным графом(взвешенная сеть). Вес графа (сети) равен сумме весов его ребер. Содержательно вес ребра может означать стоимость передачи информации между узлами, соответствующими его концам, величину потока передаваемой информации по этой дуге или ее пропускную способность и т.д. Взвешенные графы применяются для решения различных транспортных задач.

 

Подграф.

Определение 5.1.

    Граф Г называется подграфом графа G, если все вершины и ребра графа Г принадлежат графу G.

Определение 5.2.

    Дополнением графа  называется граф 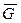с теми же вершинами, что и у графа  и с теми и только с теми ребрами, которые необходимо добавить к , чтобы получился полный граф

Операции над графами.

    Рассмотрим некоторые основные операции,

позволяющие из уже имеющихся графов получать новые графы.

1. Объединение (сумма) графов. Объединением G₁∪G₂ графов G₁= (S₁, U₁) и G₂= (S₂, U₂) называется граф (S₁∪S₂, U₁∪U₂).

2. Пересечение (произведение) графов. Пересечением G₁∩G₂ графов G₁ = (S₁, U₁) и G₂ = (S₂, U₂), где S₁∩S₂ ≠ ∅, называется граф (S₁∩S₂, U₁∩U₂).

3. Дополнение простого графа. Дополнением простого графа G = (S, U) называется простой граф, имеющий те же вершины, что и граф G, причем любые две различные вершины смежны в тогда и только тогда, когда они не смежны в G.

4. Прямое произведение графов. Граф G = (S, U) называется произведением G₁ ×G₂ графов G₁ = (S₁, U₁) и G₂ = (S₂, U₂), если S = S₁×S₂, а множество ребер U образуется следующим образом: вершины (x₁, x₂) и (y₁, y₂) смежны в графе G тогда и только тогда, когда либо вершины x₁ и y₁ совпадают, а вершины x₂ и y₂ смежны в G₂, либо вершины x₂ и y₂ совпадают, а вершины x₁и y₁ смежны в G₁.

5. Удаление вершины. Операция, заключающаяся в удалении из графа G = (S, U) вершины x и всех инцидентных ей ребер (дуг) называется операцией удаления вершины x из графа G. В результате получается подграф G (S \{x}).

6. Удаление ребра (дуги). Операция, заключающаяся в удалении ребра (дуги) u из множества ребер (дуг) U графа G = (S, U) называется операцией удаления ребра (дуги)u из графа G. Концы ребра(дуги) u не удаляются.

7. Добавление вершины. Операция, которая из графа G = (S, U) порождает граф G′= (S∪{x};U) называется операцией добавления вершины x к графу G.

8. Добавление ребра (дуги). Операция, которая из графа G= (S, U) порождает граф G′= (S∪{x, y};U ∪{(x, y)} называется операция добавления ребра (дуги) (x, y) к графу G.

9. Отождествление вершин. Пусть x и y – две произвольные вершины графа G = (S, U). Операцией отождествления вершин x и y называется операция, заключающаяся в удалении из графа G вершин x и y и присоединении к полученному графу новой вершины z, соединив ее ребром (дугой) с каждой из вершин, входящих в объединение M множеств вершин смежных с вершинами x и y в графе G. Если G – орграф, то для любой вершины a∈M присоединяется дуга (a, z), если (a, x)∈U или (a, y)∈U, и дуга (z, a), если (x, a)∈U или (y, a)∈U.

10. Стягивание ребра (дуги). Операцией стягивания ребра (дуги) называется отождествление двух смежных вершин. Граф G называется стягиваемым к графу G1, если G1 получается из G в результате некоторой последовательности стягиваний ребер (дуг).

11. Операция подразбиения ребра (дуги). Операцией подразбиения ребра (дуги) (x, y) графа G= (S, U) называется операция, заключающаяся в удалении из U ребра (дуги) (x, y), добавлении к S новой вершины z и добавлении к U \ {(x, y)} двух ребер (x, z) и (z, y).

Маршруты, цепи, циклы.

   

Рассмотрим задачу: Как можно пройти по ребрам графа, изображенного на рисунке, из вершины А₁ в вершину А₅?

Решение.

Запишем, как можно пройти:

1. (А₁А₄), (А₄А₅).

2. (А₁А₂), (А₂А₄), (А₄А₅).

3. (А₁А₄), (А₄А₂), (А₂А₁), (А₁А₄), (А₄А₅).

4. (А₁А₂), (А₂ А₄), (А₄ А₃), (А₃А₁), (А₁А₄), (А₄А₅) и другие…

В одних ребра повторяются, в других – не повторяются. Но не всякую последовательность ребер, ведущих из А₁ в А₅ называют путем из А₁ в А₅.

Определение 7.1.

    МаршрутомотА₁ до А _n в графе называется чередующаяся последовательность вершин и инцидентных им ребер, т.е. такая последовательность ребер, ведущая отА₁ до А _n, в которой каждые два соседние ребра имеют общую вершину.

Определение 7.2.

    Маршрут называется путем или цепью, если все его ребра различны, т.е. никакое ребро не встречается более одного раза.

В примере даны маршруты, при этом 1. и 2. – пути, а 3. и 4. – не пути.

Определение 7.3.

    Путь называется простой цепью или простым путем, если все его вершины (за исключением, может быть, первой и последней) различны. (Т.е. путь не проходит ни через одну из вершин графа более одного раза).

Определение 7.4.

     Цепь, в которой начальная и конечная вершины совпадают, называется циклом. Если при этом цепь – простая, то она называется простым циклом.

В примере acbdeba – цикл, но не простой; acdeba – простой цикл.

Задача.

Утверждают, что в одной компании из пяти человек каждый знаком с двумя и только с двумя другими. Возможна ли такая компания?

Решение.

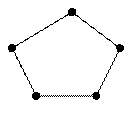Каждого из компании изобразим на рисунке кружком. Если двое знакомы, соединим соответствующие кружки отрезком.

Из рассматриваемой компании нельзя выделить ни четырехугольник, ни треугольник, поскольку тогда условие задачи будет нарушено, т.е. схема единственна.

Данный граф – цикл.

Определение 7.5.

     Если все вершины графа имеют одну и ту же степень r, то граф называется однородным графом степени r.

Например,  простой цикл является однородным графом степени 2.

Теорема 1. ( Первая теорема теории графов. Доказана Эйлером.)

Сумма степеней вершин(p, q) – графа равна удвоенному числу его ребер:                                           .

Определение 7.6.

     Длиной маршрута называется число ребер в нем, при этом каждое ребро считается столько раз, сколько оно встречается в данном пути. Длиной пути называется число ребер пути. Длиной цикла называется число ребер цикла.

 

---

Дата добавления: 2021-03-18; просмотров: 99; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!