Граничні умови на поверхні розділу
Електродинаміка і оптика.
Хвилі з довільним напрямом поширення
|
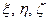 ) зі спільним початком в нулю.
) зі спільним початком в нулю.  Введена прямокутна система координат
Введена прямокутна система координат 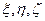 (ксі, ета, дзета), так, щоб напрям поширення хвилі співпадав з віссю
(ксі, ета, дзета), так, щоб напрям поширення хвилі співпадав з віссю  . Тоді між ортами обох систем існують такі співвідношення:
. Тоді між ортами обох систем існують такі співвідношення:
 ,
,
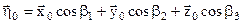 ,
,
 .
.
Електромагнітне поле хвилі в такій системі координат буде виглядати так:
 ,
, 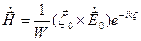 . (6.1)
. (6.1)
Введемо хвильовий вектор  , напрям якого співпадає із напрямом променя, а довжина дорівнює хвильовому числу:
, напрям якого співпадає із напрямом променя, а довжина дорівнює хвильовому числу:
 , (6.2)
, (6.2)
де 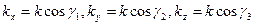 . Хвильовий вектор перпендикулярний хвильовому фронту. Для переходу до координат X, Y, Z можна записати наступну рівність:
. Хвильовий вектор перпендикулярний хвильовому фронту. Для переходу до координат X, Y, Z можна записати наступну рівність:
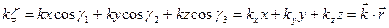 ,
,
де  – радіус-вектор точки. Таким чином, е/м поле плоскої однорідної хвилі, поширюючись в довільному напрямі
– радіус-вектор точки. Таким чином, е/м поле плоскої однорідної хвилі, поширюючись в довільному напрямі  , визначається виразом:
, визначається виразом:
 , де
, де 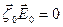 . (6.3)
. (6.3)
Оскільки  , тому швидкість переміщення хвильового фронту (фазова швидкість) вздовж осей X, Y, Z рівна:
, тому швидкість переміщення хвильового фронту (фазова швидкість) вздовж осей X, Y, Z рівна:
 ,
,  ,
,  ,
,
де 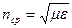 – показник заломлення середовища; с – швидкість світла в вакуумі;
– показник заломлення середовища; с – швидкість світла в вакуумі;  – швидкість світла в середовищі.
– швидкість світла в середовищі.
Цей самий результат отримаємо при розгляді 
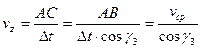 . (6.4)
. (6.4)
|
|
|
Таким чином, швидкість переміщення хвильового фронту вздовж осей координат завжди більша або рівна фазової швидкості хвилі вздовж її напряму поширення.
Швидкість переносу енергії вздовж осей координат (групова швидкість):
 ,
,  ,
,  , (6.5)
, (6.5)
і ніколи не перевищує швидкості світла с.
В ізотропному середовищі без втрат завжди:  , і є величина постійна для будь-якого напрямку.
, і є величина постійна для будь-якого напрямку.
Відбивання і заломлення е/м хвиль
Будемо розглядати гармонічний електромагнітний хвилевий процес у випадку, коли весь простір розділений площиною на два однорідних півпростори з різними властивостями. В першому середовищі задамо так звану падаючу хвилю  ,
,  , яка поширюється із нескінченності до границі під деяким кутом, і припустимо, що існує відбита хвиля
, яка поширюється із нескінченності до границі під деяким кутом, і припустимо, що існує відбита хвиля  ,
,  , яка поширюється від границі. В другому середовищі допустимо існування одної пройденої хвилі
, яка поширюється від границі. В другому середовищі допустимо існування одної пройденої хвилі 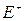 ,
,  (заломленої хвилі), яка виходить від границі в нескінченність.
(заломленої хвилі), яка виходить від границі в нескінченність.

|
Задача полягає в тому, щоб при заданій падаючій хвилі підібрати такі комплексні амплітуди і напрями поширення двох інших хвиль, щоб компоненти 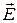 і
і  залишились неперервними на межі розділу. Для цього випадку граничні умови набудуть наступного вигляду:
залишились неперервними на межі розділу. Для цього випадку граничні умови набудуть наступного вигляду:
|
|
|
 та
та 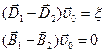 , (6.6)
, (6.6)
де індекси 1 і 2 позначають два різних середовища.
Нормальне падіння
Розпочнемо з розгляду окремого випадку, коли падаюча хвиля поширюється вздовж осі Z, тобто по нормалі до границі розділу. Напрямки поширення відбитої і пройденої хвиль є колінеарні (див. рис.).
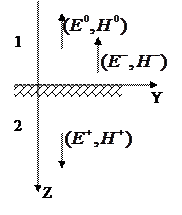
|
Для цього випадку можна записати вирази для комплексних амплітуд векторів 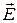 і
і  всіх трьох хвиль :
всіх трьох хвиль :
 ,
,
 , (6.7)
, (6.7)
 .
.
Введемо наступні коефіцієнти:
 ,
,  ,
,
де 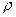 – коефіцієнт відбиття, а
– коефіцієнт відбиття, а  – коефіцієнт проходження (заломлення).
– коефіцієнт проходження (заломлення).
Виходячи з цього, можна дати наступні визначення:
– коефіцієнт відбиття – це відношення комплексних амплітуд напруженостей електричного поля відбитої хвилі до падаючої, взятих на поверхні розділу середовищ.
– коефіцієнт заломлення – це відношення комплексних амплітуд напруженостей електричного поля заломленої хвилі до падаючої, взятих на поверхні розділу середовищ.
Оскільки значення цих коефіцієнтів є комплексними величинами, тому модуль коефіцієнта відбиття (заломлення) дає відношення амплітуд, а аргумент – різницю фаз відбитої (заломленої) і падаючої хвиль на поверхні розділу середовищ.
|
|
|
Тоді із (6.7) випливає, що:  та
та  .
.
Припускаючи в (6.7) Z=0, внесемо ці вирази в граничні умови і отримуємо:
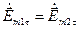 Þ
Þ  Þ
Þ  . (6.8)
. (6.8)
 Þ
Þ  Þ
Þ  . (6.9)
. (6.9)
Звідки можна записати:

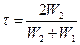 . (6.10)
. (6.10)
Розглянемо декілька варіантів поширення хвилі.
Випадок 1. Нехай  або
або 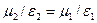 , тоді
, тоді  – випадок повного проходження електромагнітної хвилі.
– випадок повного проходження електромагнітної хвилі.
Випадок 2. Коли W1 та W2 є дійсні, тоді можна спостерігати повне відбиття. Воно має місце, коли  , а це, виходячи з модифікованої формули (6.10):
, а це, виходячи з модифікованої формули (6.10):  , буде при умові, якщо
, буде при умові, якщо  або
або  , а на практиці це означає, що
, а на практиці це означає, що  або
або 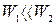 .
.
Розглянемо приклад ідеального провідника, для якого  . Оскільки для ідеального провідника:
. Оскільки для ідеального провідника:  , тоді
, тоді  . З формули (6.10) слідує, що:
. З формули (6.10) слідує, що:  , тобто буде повне відбиття. При таких умовах виникає можливість утворення стоячої хвилі.
, тобто буде повне відбиття. При таких умовах виникає можливість утворення стоячої хвилі.
Нахилене падіння
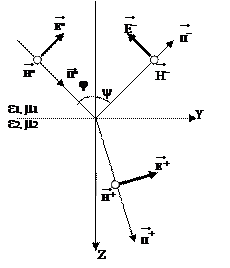
Площина, в якій лежать промінь і нормаль до границі розділу, називають площиною падіння. Є два види поляризацій: перпендиндикулярна (горизонтальна-зліва) і паралельна (вертикальна):

| 
|
З неперервності тангенціальних складових векторів 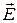 і
і  на межі розділу виходить, що залежності полів трьох хвиль від координат Y і Z є однакові. Тому промені відбитої і заломленої хвиль лежать в площині падіння, а проекції на вісь Z є рівні. Пропускаючи виведення, приведемо відразу значення коефіцієнтів відбиття і заломлення для перпендикулярної поляризації:
на межі розділу виходить, що залежності полів трьох хвиль від координат Y і Z є однакові. Тому промені відбитої і заломленої хвиль лежать в площині падіння, а проекції на вісь Z є рівні. Пропускаючи виведення, приведемо відразу значення коефіцієнтів відбиття і заломлення для перпендикулярної поляризації:
|
|
|
 ,
,  . (6.11)
. (6.11)
та для паралельної поляризації:
 ,
,  . (6.12)
. (6.12)
Вирази (6.11) і (6.12) є так звані формули Френеля.
Виходячи із останніх малюнків, легко можна записати величини повних е/м полів в заданій системі координат. Покажемо це. Нехай комплексні амплітуди напруженостей поля виражаються наступними формулами :
 , та
, та 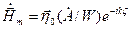 .
.
Якщо користуватися правилами перетворення ортів і координат, запишемо ці формули в основній системі координат (X, Y, Z), для якої будемо мати:
 (6.12а)
(6.12а)
Розглянемо випадок перпендикулярної поляризації. Тоді для падаючої хвилі (див. рис.), коли  ,
,  та
та 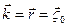 , можна записати величини кутів всіх її направляючих косинусів:
, можна записати величини кутів всіх її направляючих косинусів:
a10=0°; a20=90°; a30=90°;
b10=90°; b20=j; b30=90°+j; (6.13)
g10=90°; g20=90°–j; g30=j.
З системи виразів (6.12а), використовуючи значення кутів з (6.13), можна записати:
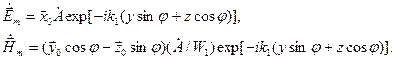 .
.
Аналогічно можна записати величини направляючих кутів для заломленої хвилі:
a1+=0°; a2+=90°; a3+=90°;
b1+=90°; b2+=q; b3+=90°+q; (6.14)
g1+=90°; g2+=90°–q; g3+=q.
Якщо для поля падаючої хвилі значення комплексної амплітуди залишалося без змін, то для заломленої хвилі потрібно врахувати те, що хвиля пройшла з першого середовища в друге, тому потрібно ввести поправочний множник, а саме коефіцієнт заломлення, тому: 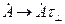 . Виходячи з цього можна отримати:
. Виходячи з цього можна отримати:

Аналогічні результати можна отримати і для випадку паралельної поляризації. Виходячи з рис. запишемо поле тільки для відбитої хвилі для якої направляючі кути рівні:
a1– =90°; a2– =180°–j; a3– =90°+j;
b1– =180°; b2– =90°; b3– =90°;
g1– =90°; g2– =90°–j; g3– =180°–j;
а саме поле аналогічно можна записати так:

Закони відбиття і заломлення
Припустимо, що на поверхню розділу двох лінійних, ізотропних і однорідних середовищ з першого падає плоска однорідна, вертикально поляризована електромагнітна хвиля. Три хвилі, що утворюються в результаті такого падіння, можна записати як плоскі хвилі, що поширюються у відповідних напрямах. Тому можна перейти до вивчення основних законів оптики для відбитої і заломленої хвиль:
1). Кут падіння  рівний куту відбиття
рівний куту відбиття  :
: 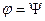 . (6.14а)
. (6.14а)
2). Відношення синус кута заломлення  до синуса кута падіння
до синуса кута падіння  є величиною сталою, яка рівна відносному коефіцієнту заломлення
є величиною сталою, яка рівна відносному коефіцієнту заломлення  одного середовища по відношенню до іншого:
одного середовища по відношенню до іншого:
 , (6.15)
, (6.15)
де  ,
, 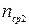 – коефіцієнти заломлення середовищ; k 1 i k 2 – їх хвильові числа.
– коефіцієнти заломлення середовищ; k 1 i k 2 – їх хвильові числа.
Записані рівності (6.14а) і (6.15) називаються законами Снелліуса.
Визначимо тут ще загальновідомий кут Брюстера. Зазначимо, що кут Брюстера – це є кут повного проходження хвилі з одного середовища в інше. Це можливо тільки при паралельній поляризації. Коефіцієнт відбиття 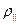 при цьому дорівнює нулю, тобто
при цьому дорівнює нулю, тобто
 , Þ
, Þ  – вивести самостійно (6.16)
– вивести самостійно (6.16)
Шуканий кут Брюстера можна визначити за наступною формулою:
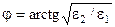 . (6.17)
. (6.17)
Якщо використати подібний метод для знаходження кута Брюстера для випадку перпендикулярної поляризації, то рівність (6.36) у цьому випадку набуде наступного вигляду:
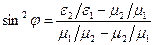 .
.
При m1= m2 не існує кута j, що задовольняє цю рівність, а відповідно, повне проходження хвилі неможливе.
Повне внутрішнє відбиття
Явище повного внутрішнього відбиття від поверхні розділу середовищ може відбуватися тоді, коли кут падіння більший від граничного 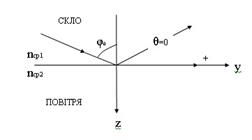 . Тобто, це можливо при умові:
. Тобто, це можливо при умові: 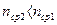 . Тоді, згідно закону Снелліуса
. Тоді, згідно закону Снелліуса  при
при  :
: 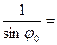
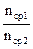 Þ
Þ  – кут повного внутрішнього відбивання . В першому середовищі швидкість поширення вздовж осі Y:
– кут повного внутрішнього відбивання . В першому середовищі швидкість поширення вздовж осі Y:
 , тобто швидкість поширення вздовж осі Y має
, тобто швидкість поширення вздовж осі Y має  (оскільки значення
(оскільки значення 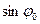 в попередній формулі знаходиться в межах [-1,1]) , де
в попередній формулі знаходиться в межах [-1,1]) , де  – фазова швидкість хвилі в цьому середовищі. А в напрямку осі (-Z) поле являє собою стоячу хвилю , так як
– фазова швидкість хвилі в цьому середовищі. А в напрямку осі (-Z) поле являє собою стоячу хвилю , так як  .
.
Граничні умови на поверхні розділу
Діелектрик-метал
 На відміну від звичайних граничних умов, що зв’язують значення складових поля на границі розділу в різних середовищах, граничні умови Щукіна–Леонтовича виражають зв’язок між складовими векторів
На відміну від звичайних граничних умов, що зв’язують значення складових поля на границі розділу в різних середовищах, граничні умови Щукіна–Леонтовича виражають зв’язок між складовими векторів  і
і  в одному середовищі. Немагнітний метал
в одному середовищі. Немагнітний метал  являє для електромагнітної хвилі дуже густе оптичне середовище , в якому модуль показника заломлення:
являє для електромагнітної хвилі дуже густе оптичне середовище , в якому модуль показника заломлення:
 через це з
через це з  виходить, що на межі розділу повітря-метал (див. рис.) кут заломлення:
виходить, що на межі розділу повітря-метал (див. рис.) кут заломлення:
 . (6.18)
. (6.18)
Незалежно від кута падіння  кут заломлення близький до 0, тобто е/м хвиля поширюється в металі майже по нормалі до його поверхні. Дотичні складові електричного і магнітного полів на поверхні розділу неперервні:
кут заломлення близький до 0, тобто е/м хвиля поширюється в металі майже по нормалі до його поверхні. Дотичні складові електричного і магнітного полів на поверхні розділу неперервні:
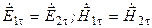 .
.
Так як кут заломлення для будь-яких хвиль при переході розділу діелектрик-метал близький до нуля, тому для довільного поля в діелектрику має місце рівність:
 , (6.19)
, (6.19)
де  – орт нормалі, спрямований в метал;
– орт нормалі, спрямований в метал;
 – поверхневий опір;
– поверхневий опір; 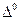 – називають глибиною проник -нення. Вираз (6.19) є г ранична умова Щукіна – Леонтовича.
– називають глибиною проник -нення. Вираз (6.19) є г ранична умова Щукіна – Леонтовича.
Граничні умови Щукіна–Леонтовича справедливі, якщо радіус кривизни  . На межі метал – діелектрик протікає поверхневий струм:
. На межі метал – діелектрик протікає поверхневий струм:
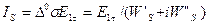 . (6.20)
. (6.20)
Для ідеального провідника:
 ,
,
тому виходить, що 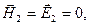 а на його поверхні виконуються граничні умови:
а на його поверхні виконуються граничні умови:
 (6.21)
(6.21)
Дата добавления: 2021-03-18; просмотров: 68; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
