Определить кратчайший путь из заданной вершины в остальные.
Для реализации данной процедуры используется алгоритм Дейкстры.
Ориентированный граф G = (V, E), источник v0 ∈ V и функция l, отображающая множество E x E во множество неотрицательных вещественных чисел. Полагаем l(v i , v j) = +∞, если ребро (vi , vj), vi /= vj , не принадлежит графу, и l(vi , vj) = 0.
Для каждого v0 ∈ V наименьшая сумма меток на ребрах из P, взятая по всем путям P, идущим из v0 в v.
Строим такое множество S ⊆ V, что кратчайший путь из источника в каждый узел v ∈ S целиком лежит в S. Массив D[v] содержит стоимость текущего кратчайшего пути из v0 в v, который проходит только через узлы из S.
Построение минимального остовного дерева алгоритмом Крускала
Остовное дерево - ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины. Можно сказать, что остовное дерево состоит из некоторого подмножества рёбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рёбрам, и в нём нет циклов, то есть из любой вершины нельзя попасть в саму себя, не пройдя какое-то ребро дважды. Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе - это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов, входящих в него рёбер.
Алгоритм Крускала изначально помещает каждую вершину в своё дерево, а затем постепенно объединяет эти деревья, объединяя на каждой итерации два некоторых дерева некоторым ребром. Перед началом выполнения алгоритма, все рёбра сортируются по весу (в порядке неубывания). Затем начинается процесс объединения: перебираются все рёбра от первого до последнего (в порядке сортировки), и если у текущего ребра его концы принадлежат разным поддеревьям, то эти поддеревья объединяются, а ребро добавляется к ответу. По окончании перебора всех рёбер все вершины окажутся принадлежащими одному поддереву, и ответ найден.
|
|
|
В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связан, то остов найден не будет.
Разработка программы, реализующей алгоритмы на графах
В рамках выполнения курсовой работы была необходимо разработать программу на языке Паскаль реализующую алгоритмы на графах.
Исходные данные
Исходными данными является ориентированный граф. Вершин в графе 6, рёбра графа имеют неотрицательный вес.
Исходный граф представлен на рисунке 2.1.
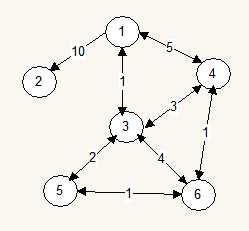
Рис. 2.1. - Исходный граф.
Структура данных
Для хранения данных в программе используется матрица А размером n x n, определенная как array[1..n,1..n] of integer, где n – константа, определяющая максимальное количество вершин.
|
|
|
Результаты работы программы
В программе организовано меню, с помощью которого активируются процедуры, а результаты их работы выводятся на экран.
На рисунке 2.2 показано меню программы и матрица смежности графа.
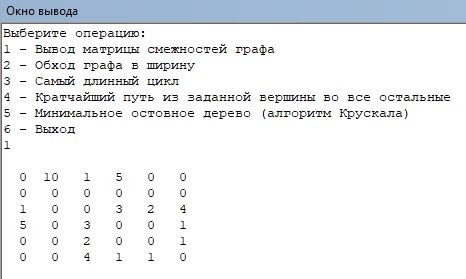
Рис. 2.2 – Меню и матрица смежности
Меню организовано с помощью метода case. Вывод матрицы происходит с использованием двух циклов: один внешний и один внутренний.
На рисунке 2.3 показан поиск самого длинного цикла.
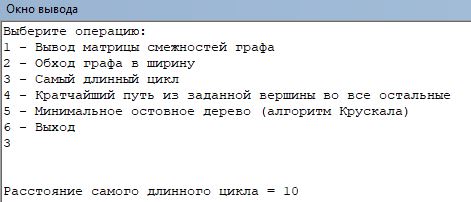
Рис. 2.3 – Поиск самого длинного цикла
Процедура Cycle находит расстояние длинного цикла и выписывает его.
На рисунке 2.4 показан обход графа в ширину.
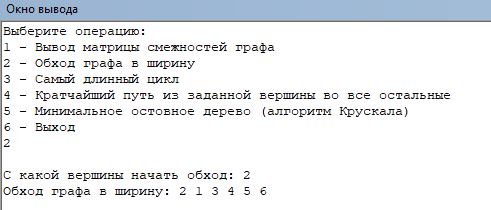
Рис. 2.4. – Обход графа в щирину
Вводится начальная вершина, после с помощью процедуры B FS совершается обход дерева.
На рисунке 2.5 результат поиска кратчайшего пути из заданной вершины во все остальные.
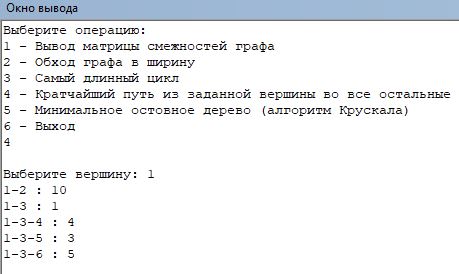
Рис.2.5 – Поиск кратчайшего пути из заданной вершины во все остальные
Для поиска самых коротких путей из вершины используются процедуры Dejkstra и prDejkstra. Процедура Dejkstra находит кратчайшие пути, а prDejkstra выводит их на экран с указанием длины пути.
|
|
|
На рисунке 2.6 показан результат работы алгоритма Крускала.

Рис. 2.6 – Работа алгоритма Крускала.
В результате работы процедуры Kruskal выводятся ребра, включаемые в дерево, а так же длина остовного дерева.
Заключение
В процессе работы над курсовой работой были изучены алгоритмы на графах (определение самого длинного цикла в графе, обход графа в ширину, определение кратчайшего пути из заданной вершины во все остальные, построение минимального остовного дерева с помощью алгоритма Крускала).
В качестве практической части была разработана программа на языке Паскаль реализующая алгоритмы на графах:
- определение самого длинного цикла в графе;
- выполнение обхода графа в ширирну;
- определение кратчайшего пути из заданной вершины во все остальные;
- построение минимального остовного дерева с помощью алгоритма Крускала.
Исходными данными является ориентированный граф. Вершин в графе 6, рёбра графа имеют неотрицательный вес.
Программа прошла проверку на тестовых данных.
Литература
1. Ахо, А. Структуры данных и алгоритмы / А. Ахо, Дж. Хопкрофт, Дж. Ульман. М.: Изд. дом «Вильямс», 2001. 384с.
|
|
|
2. Вирт, Н. Алгоритмы и структуры данных / Н. Вирт. СПб.: Невский диалект, 2001. 352с.
3. Вирт, Н. Алгоритмы + структуры данных = программы / Н. Вирт. М.: Мир, 1985. 360с.
4. Ковалев, И. В. Моделирование и оптимизация параллельных процессов в информационно-управляющих системах / И. В. Ковалев, Р. Ю. Царев. Красноярск: ИПЦ КГТУ, 2003. 111с.
Приложение
Const
n = 6; INF = 10000;
Type
graf = array [1..n,1..n] of integer;
visit = array [1..n] of Boolean; // посещенные вершины
mas = array [1..n] of integer; // массив кратчайших путей
NI = array [1..2] of integer;
VI = array of NI; // массив пар вершин
Var
G, dG: graf;
sdG: VI;
i, j, k, sum: integer;
s: string;
q: integer := 1;
mark, mark1: visit;
D: mas; // массив кратайших путей
P: mas; //массив предшествующих вершин
//--------------------------------------------------------
// ОБХОД ГРАФА В ШИРИНУ
//--------------------------------------------------------
function Not_Visited(mark:visit):integer; // Непосещённая вершина
Begin
for var j:=1 to n do
Begin
if mark[j]=false then // доходим до непосещенной вершины
begin
result:=j; // результат вычисления функции - вершина
exit;
end;
end;
result:=0;
end;
procedure BFS(start:integer); // Обход в ширину
Var
u:integer; // вершины графа
Begin
s:=s+inttostr(start)+' ';
mark[start]:=true;
for u:=1 to n do
if (G[start,u]<>0) and (not mark[u]) then // есть ребро и вершина не пройдена
Begin
mark[u]:=true; // вершина пройдена
s:=s+inttostr(u)+' ';
end;
q:=Not_Visited(mark);
if q=0 then exit // если не осталось непройденных вершин
else BFS(q);
end;
//--------------------------------------------------------
// САМЫЙ ДЛИННЫЙ ЦИКЛ
//--------------------------------------------------------
procedure Cycle;
Const
min = 0;
Var
p: array[1..n, 1..n] of integer;
a: array[1..n, 1..n] of integer;
i, j, k, u, max: integer;
Begin
for i := 1 to n do
for j := 1 to n do
a[i, j] := G[i, j];
for i := 1 to n do
for j := 1 to n do
if a[i, j] = 1 then a[i, j] := min;
for k := 1 to n do
for i := 1 to n do
for j := 1 to n do
if a[i, k] - a[k, j] > a[i, j]
then begin
a[i, j] := a[i, k] - a[k, j];
p[i, j] := k;
end;
writeln;
max := a[1, 1];
u := 1;
for i := 1 to n do
for j := i to n do
if i = j
Then begin
if (a[i, j] > max) AND (a[i, j] < INF)
then begin
max := a[i, j];
u := j;
end;
end;
writeln('Расстояние самого длинного цикла = ', max);
end;
//--------------------------------------------------------
// КРАТЧАЙШИЙ ПУТЬ ИЗ ЗАДАННОЙ ВЕРШИНЫ ВО ВСЕ ОСТАЛЬНЫЕ
//--------------------------------------------------------
procedure Dejkstra(k:integer); // Алгоритм Дейкстра (поиск кратчайшего пути)
Var
minI:integer;
minV:integer:=INF;
Begin
mark[k]:=true;
for var i:=1 to n do
Begin
if (i=k) or (G[k,i]=0) or (mark[i]=true) then continue;
if D[i]>(G[k,i]+D[k]) then
Begin
D[i]:=G[k,i]+D[k];
P[i]:=k; // предшествующая вершина
end;
end;
for var i:=1 to n do
Begin
if (G[k,i]<minV) and (mark1[i]<>true) and (G[k,i]<>0) then
Begin
minV:=G[k,i];
minI:=i;
end;
end;
if minV<INF then
Begin
mark1[minI]:=true;
Dejkstra(minI);
end;
end;
procedure prDejkstra(u:integer; way:string); // показывает результат Dejkstra()
Var
way1:string;
Begin
for var i:=1 to n do
Begin
if P[i]=u then
Begin
way1:='-'+i;
writeln(way+way1+' : '+D[i]);
prDejkstra(i,way+way1);
end;
end;
end;
//--------------------------------------------------------
// МИНИМАЛЬНОЕ ОСТОВНОЕ ДЕРЕВО С ПОМОЩЬЮ АЛГ. КРУСКАЛА
//--------------------------------------------------------
function disorient(dG: graf): graf; // Преобразование графа в неориентированный
Begin
for var i := 1 to n do
for var j := i + 1 to n do
Begin
if dG[i,j] = 0 then
if dG[j,i] = 0 then continue
else dG[i,j] := dG[j,i]
else dG[j,i] := dG[i,j];
end;
result := dG;
end;
procedure Kruskal(); // Алгоритм Крускала
Type
wSet = set of integer;
Var
x, k, n1, n2, n3, n4, j, k1, k2: integer;
z: array [1..n] of wSet;
sec: NI;
Begin
for var i := 1 to n do // смотрим вершины, записываем их в массив
for j := i + 1 to n do
if dG[i][j] <> 0 then
Begin
x += 1;
setlength(sdG, x);
sdG[x - 1][1] := i; sdG[x - 1][2] := j;
end;
k := x div 2; // сортировка
while k > 0 do
Begin
for var i := 1 to x - k do
Begin
j := i;
n1 := sdG[j - 1][1]; n2 := sdG[j - 1][2];
n3 := sdG[j + k - 1][1]; n4 := sdG[j + k - 1][2];
while (j > 0) and (dG[n1][n2] > dG[n3][n4]) do
Begin
sec := sdG[j - 1];
sdG[j - 1] := sdG[j + k - 1];
sdG[j + k - 1] := sec;
j := j - k;
if j > 0 then
Begin
n1 := sdG[j - 1][1]; n2 := sdG[j - 1][2];
n3 := sdG[j + k - 1][1]; n4 := sdG[j + k - 1][2];
end;
end;
end;
k := k div 2;
end;
for var i := 1 to n do
z[i] := [i];
for var i := 1 to x do
Begin
k1 := 0; k2 := 0;
for j := 1 to n do
if sdG[i - 1][1] in z[j] then k1 := j
else if sdG[i - 1][2] in z[j] then k2 := j;
if(k1 = 0) or (k2 = 0) then continue;
if k1 <> k2 then
Begin
z[k1] := z[k1] + z[k2];
z[k2] := [];
sum := sum + dG[sdG[i - 1][1]][sdG[i - 1][2]];
s := s + inttostr(sdG[i - 1][1]) + '-' + inttostr(sdG[i - 1][2]) + ' ';
end;
end;
end;
//--------------------------------------------------------
// ТЕЛО ПРОГРАММЫ
//--------------------------------------------------------
Begin
G[1,1]:=0; G[2,1]:=0; G[3,1]:=1; G[4,1]:=5; G[5,1]:=0; G[6,1]:=0;
G[1,2]:=10; G[2,2]:=0; G[3,2]:=0; G[4,2]:=0; G[5,2]:=0; G[6,2]:=0;
G[1,3]:=1; G[2,3]:=0; G[3,3]:=0; G[4,3]:=3; G[5,3]:=2; G[6,3]:=4;
G[1,4]:=5; G[2,4]:=0; G[3,4]:=3; G[4,4]:=0; G[5,4]:=0; G[6,4]:=1;
G[1,5]:=0; G[2,5]:=0; G[3,5]:=2; G[4,5]:=0; G[5,5]:=0; G[6,5]:=1;
G[1,6]:=0; G[2,6]:=0; G[3,6]:=4; G[4,6]:=1; G[5,6]:=1; G[6,6]:=0;
i:=1;
while true do
Begin
writeln('Выберите операцию:');
writeln('1 - Вывод матрицы смежностей графа');
writeln('2 - Обход графа в ширину');
writeln('3 - Самый длинный цикл');
writeln('4 - Кратчайший путь из заданной вершины во все остальные');
writeln('5 - Минимальное остовное дерево (алгоритм Крускала)');
writeln('6 - Выход');
readln(k);
writeln;
case k of
1:begin
Repeat
for j:=1 to n do begin write(G[i,j]:3,' '); end;
i+=1;
writeln;
until i>n;
writeln;
end;
2:begin
write('С какой вершины начать обход: '); readln(j);
BFS(j);
writeln('Обход графа в ширину: ',s);
for i:=1 to n do begin mark[i]:=false; end; q:=1; s:='';
writeln;
end;
3:begin
Cycle();
end;
4:begin
write('Выберите вершину: '); readln(j);
for i:=1 to n do
if i<>j then D[i]:=INF
else D[i]:=0;
Dejkstra(j);
for i:=1 to n do
if mark[i]=false then Dejkstra(i); // остались ли не пройденные вершины?
for i:=1 to n do mark[i]:=false;
s:=inttostr(j);
prDejkstra(j,s);
for i:=1 to n do P[i]:=0; s:='';
writeln;
end;
5:begin
dG := G;
dG := disorient(dG);
Kruskal;
writeln('Построение остовного дерева: ', s);
writeln('Длина остовного дерева: ', sum);
s:=''; sum:=0;
writeln;
end;
6:exit;
end;
end;
end.
Дата добавления: 2021-03-18; просмотров: 99; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
