Решение уравнений с применением графического метода
Лекция 35.
Тема «Решение уравнений с применением всех приемов (разложения на множители, введения новых неизвестных, подстановок, графического метода)»
План лекции:
1.Решение уравнений с помощью разложения на множители.
2.Решение уравнений с помощью введения новых переменных.
3.Решение уравнений с помощью подстановки.
4.Решение уравнений графическим методом.
Основные понятия и определения:
решение уравнения, корень уравнения, разложение на множители.
Решение уравнений с помощью разложения на множители
Определение. Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.
Свойство. Произведение двух выражений будет иметь нулевой результат, если хотя бы один из данных множителей будет равен нулю.
Многочлен уравнения можно представить в виде произведения двух множителей. Но так как этот многочлен должен быть равен нулю, то, соответственно и произведение данных множителей, тоже будет нулевым. А это значит, что каждый из этих множителей будет равен нулю.

Уравнение вида, когда в обеих частях неравенства находятся выражения.
Тогда это уравнение решается следующим образом. Все члены переносятся в левую часть. Так получается нулевое значение правой части уравнения. А затем полученное в левой части выражение упрощается, и приводится к виду, который позволяет представить это выражение в виде произведения.
|
|
|

Решение уравнений с применением приема введения новых неизвестных
Метод введения новой переменной
1. В уравнении какая-то его часть заменяется другой переменной (a,y,t,...) (прежнее неизвестное одновременно с новым в уравнении быть не может).
2. Решается новое уравнение.
3. Возвращаются к обозначенному и, используя полученное число (корни), вычисляется требуемое неизвестное.
Пример:
Реши уравнение (2x − 21)2 − 5(2x − 21) + 4 = 0.
Это уравнение можно решить и без использования новой переменной (раскрываются скобки по формуле разности квадратов и т. д.), но решение будет длинным и с большими числами.
Используем то, что обе скобки равны.
Обозначаем 2x−21 = y. Получается простое квадратное уравнение:
y2 − 5y + 4 = 0 по теореме Виета y1 = 4, y2 = 1.
Возвращаемся к обозначенному:
1) 2x – 21 = 4;
2x = 25;
x = 12,5.
2) 2x – 21 = 1;
2x = 22;
x = 11.
Ответ: x = 12,5; x = 11.
Методом введения новой переменной решаются биквадратные уравнения:
ax4 + bx2 + c = 0, где a, b, c∈R x2 = y.
ay2 + by + c = 0.
В биквадратных уравнениях всегда используется новая переменная.
Получается квадратное уравнение.
|
|
|
Решение уравнений с применением метода подстановок
Суть метода подстановки:
Выразить одну переменную через другую из любого уравнения системы.
Подставить полученное выражение в другое уравнение системы и решить как одно уравнение с одной неизвестной переменной.
Зная одну переменную, найти другую из исходного уравнения.
Метод позволяет свести решение системы к решению одного уравнения с одним неизвестным.

Решение уравнений с применением графического метода
Для того чтобы решить уравнение графическим методом, надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций.
Например, дано такое уравнение:
x² – 2x – 1 = 0.
Чтобы решить подобное уравнение графически, представим его в таком виде:
x² = 2x + 1
Из такого представления уравнения следует, что требуется найти такие значения x, при которых левая часть будет равна правой.
Как известно, графиком функции y = x² является парабола, а y = 2x + 1 — прямая.
Координата x точек координатной плоскости, лежащих как на первом графике, так и на втором (то есть точек пересечения графиков) как раз и являются теми значениями x, при которых левая часть уравнения будет равна правой. Другими словами, координаты x точек пересечения графиков являются корнями уравнения.
|
|
|
Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.
Рассмотрим пример попроще:
x² – 2x = 0 или x² = 2x
Построим графики функций y = x² и y = 2x:
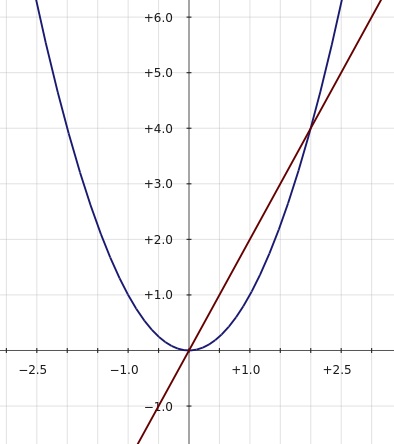
Как видно из чертежа, парабола и прямая пересекаются в точках (0; 0) и (2; 4). Координаты x этих точек соответственно равны 0 и 2. Значит, уравнение x² – 2x = 0 имеет два корня — x1 = 0, x2 = 2.
Дата добавления: 2021-03-18; просмотров: 652; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
