ПЗ 12. Полином Жегалкина, линейность, самодвойственность функций
Ответы
ПЗ 1 Множества
Задание 1. а. 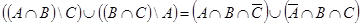 . б.
. б. 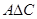 .
.
в. 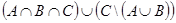 . г.
. г. 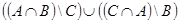 .
.
д. 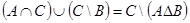 . е.
. е. 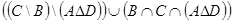 .
.
ж. 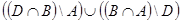 . з.
. з. 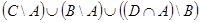 .
.
и. 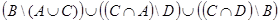 . к.
. к. 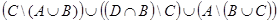 .
.
л. 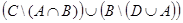 . м.
. м. 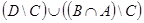 .
.
Задание 2.
1) а. нет. б. нет в. да. 2) нет. 3) 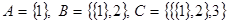 AÎB, BÎC, но AÏC.
AÎB, BÎC, но AÏC.
Задание 3.
а. Будем использовать свойство отношения включения множеств: два множества равны, если являются подмножествами друг друга. Таким образом, нужно показать, что множество 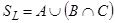 , описанное в левой части равенства, является подмножеством множества
, описанное в левой части равенства, является подмножеством множества 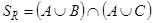 , описанного в правой части, и одновременно
, описанного в правой части, и одновременно 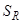 является подмножеством
является подмножеством 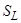 .
.
Докажем сначала вложение 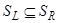 . Для этого возьмем произвольный элемент
. Для этого возьмем произвольный элемент 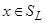 , т.е.
, т.е. 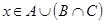 . По определению операций объединения и пересечения множеств, это означает, что или
. По определению операций объединения и пересечения множеств, это означает, что или 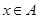 , или
, или 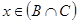 . Коротко это записывается так:
. Коротко это записывается так: 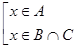 (квадратная скобка обозначает связку «или» между условиями, записанными внутри). В свою очередь, последнее утверждение равносильно следующему:
(квадратная скобка обозначает связку «или» между условиями, записанными внутри). В свою очередь, последнее утверждение равносильно следующему: 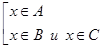 . Это можно записать короче:
. Это можно записать короче: 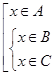 (фигурная скобка обозначает связку «и» между условиями, записанными внутри). Последнее утверждение можно трактовать так:
(фигурная скобка обозначает связку «и» между условиями, записанными внутри). Последнее утверждение можно трактовать так: 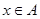 или
или 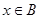 и одновременно
и одновременно 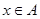 или
или 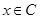 , т.е.
, т.е. 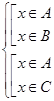 . Это в свою очередь означает, что
. Это в свою очередь означает, что 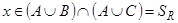 . Таким образом, любой элемент множества
. Таким образом, любой элемент множества 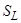 является элементом множества
является элементом множества 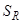 , что доказывает вложение
, что доказывает вложение 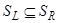 .
.
Докажем теперь вложение 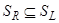 . Пусть теперь
. Пусть теперь 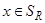 , т.е.
, т.е. 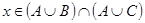 , что по определению равносильно
, что по определению равносильно 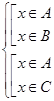 . Здесь возможны два варианта: либо
. Здесь возможны два варианта: либо 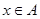 (это условие есть во всех предлагающихся наборах «или»), либо
(это условие есть во всех предлагающихся наборах «или»), либо 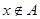 . Во втором случае элемент x обязан принадлежать множеству B (из первой скобки «или») и множеству C (из второй скобки «или»), то есть
. Во втором случае элемент x обязан принадлежать множеству B (из первой скобки «или») и множеству C (из второй скобки «или»), то есть 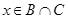 . Следовательно,
. Следовательно, 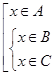 , что означает принадлежность элемента x левой части равенства
, что означает принадлежность элемента x левой части равенства 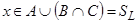 . Значит,
. Значит, 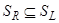 .
.
|
|
|
Из доказанных вложений 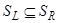 и
и 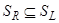 делается вывод о равенстве
делается вывод о равенстве 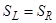 или
или 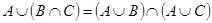 , что и требовалось доказать.
, что и требовалось доказать.
б. Знак « 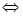 » предполагает доказательство в два этапа:
» предполагает доказательство в два этапа: 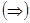 из заданного равенства, стоящего в левой части нужно доказать вложение из правой части;
из заданного равенства, стоящего в левой части нужно доказать вложение из правой части; 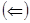 из условия вложенности множества A в C доказать выполнение равенства из левой части.
из условия вложенности множества A в C доказать выполнение равенства из левой части.
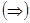 Пусть выполняется равенство
Пусть выполняется равенство 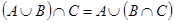 и элемент
и элемент 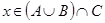 .
.
Это значит, что
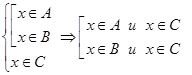 .
. 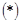
Если же элемент 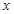 принадлежит правой части равенства
принадлежит правой части равенства 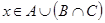 , то
, то
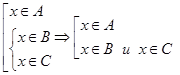 .
. 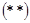
Видно, что последние условия в 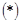 и
и 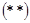 совпадают. Тогда из равенства
совпадают. Тогда из равенства 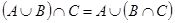 следует равносильность утверждений
следует равносильность утверждений 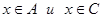 и
и 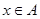 , то есть все элементы из множества A лежат во множестве C, что возможно лишь в случае вложенности
, то есть все элементы из множества A лежат во множестве C, что возможно лишь в случае вложенности 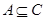 .
.
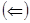 Пусть относительно множеств A и C известно, что
Пусть относительно множеств A и C известно, что 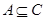 . Тогда, очевидно, что
. Тогда, очевидно, что 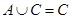 ,
, 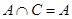 (нетрудно доказать это самостоятельно). Докажем равносильность
(нетрудно доказать это самостоятельно). Докажем равносильность 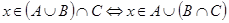 , что доказывает выполнение равенства
, что доказывает выполнение равенства 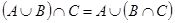 .
.
|
|
|
Пусть снова 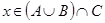 . Это равносильно утверждению
. Это равносильно утверждению  , которое ввиду выполнения условия
, которое ввиду выполнения условия 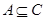 можно переписать так:
можно переписать так: 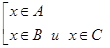 (так как условия
(так как условия 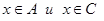 и
и 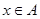 в данном случае равносильны). Можно заметить, что теперь условие принадлежности элемента
в данном случае равносильны). Можно заметить, что теперь условие принадлежности элемента 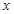 левой части доказываемого равенства полностью совпадает с условием
левой части доказываемого равенства полностью совпадает с условием 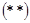 принадлежности элемента
принадлежности элемента 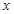 правой части. Следовательно, равенство доказано.
правой части. Следовательно, равенство доказано.
в. Пусть 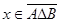 . Это значит, что
. Это значит, что 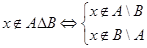 . Построим отрицание утверждения
. Построим отрицание утверждения
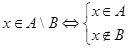 .
. 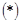
Возможны два варианта: либо 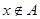 , что очевидно, либо
, что очевидно, либо 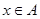 , но тогда, чтобы не нарушать условие
, но тогда, чтобы не нарушать условие 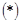 , должно выполняться условие
, должно выполняться условие 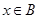 . Таким образом,
. Таким образом, 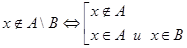 . Тогда условие
. Тогда условие 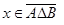 равносильно
равносильно
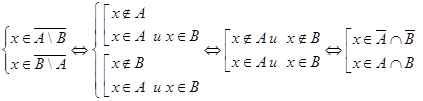 .
.
Последнее означает принадлежность элемента 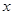 правой части равенства, то есть
правой части равенства, то есть 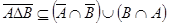 . Поскольку была построена цепочка равносильных утверждений, то верно и обратное вложение
. Поскольку была построена цепочка равносильных утверждений, то верно и обратное вложение 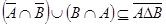 . Таким образом, равенство доказано.
. Таким образом, равенство доказано.
г. 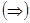 Пусть верно равенство
Пусть верно равенство 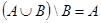 . Распишем левую часть этого равенства:
. Распишем левую часть этого равенства: 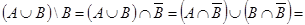
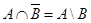 . Равенство левой и правой частей теперь можно записать как
. Равенство левой и правой частей теперь можно записать как 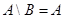 , что возможно лишь в случае непересекающихся множеств A и B, то есть
, что возможно лишь в случае непересекающихся множеств A и B, то есть 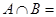 Æ.
Æ.
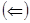 Пусть
Пусть 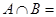 Æ. Нужно доказать справедливость равенства
Æ. Нужно доказать справедливость равенства 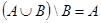 . Проводя аналогичные операции с левой частью доказываемого равенства, получим
. Проводя аналогичные операции с левой частью доказываемого равенства, получим 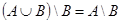 . Так как, по условию,
. Так как, по условию, 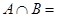 Æ, то
Æ, то 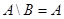 и, следовательно,
и, следовательно, 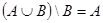 .
.
|
|
|
д. 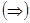 Пусть верно равенство
Пусть верно равенство 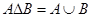 . Его левая часть:
. Его левая часть: 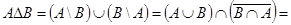
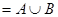 , последнее равенство возможно лишь в случае, когда
, последнее равенство возможно лишь в случае, когда 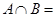 Æ.
Æ.
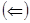 Пусть
Пусть 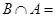 Æ. Тогда докажем, что
Æ. Тогда докажем, что 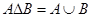 :
:
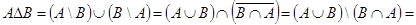
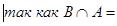 Æ
Æ 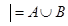 , что и требовалось доказать.
, что и требовалось доказать.
е. 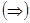 Пусть верно равенство
Пусть верно равенство 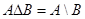 . Его левая часть равна
. Его левая часть равна 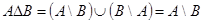 , что возможно лишь при условии, что
, что возможно лишь при условии, что 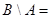 Æ, то есть
Æ, то есть 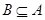 .
.
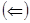 Пусть
Пусть 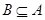 , т.е.
, т.е. 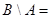 Æ. Тогда, очевидно, будет верно
Æ. Тогда, очевидно, будет верно 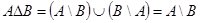 , что и требовалось доказать.
, что и требовалось доказать.
ж. Пусть 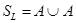 ,
, 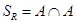 ,
, 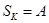 .
.
1) Докажем 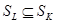 :
: 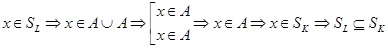 .
.
Докажем 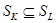 :
: 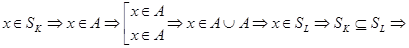
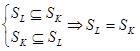 .
.
2) Докажем 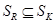 :
: 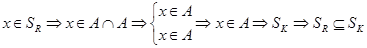 .
.
Докажем 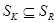 :
: 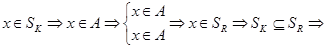
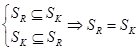 .
.
3) 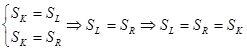 , т.е.
, т.е. 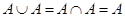 .
.
з. Пусть 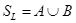 ,
, 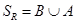 .
.
1) Докажем 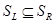 :
: 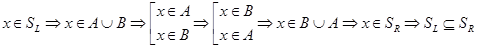 .
.
2) Докажем 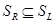 :
: 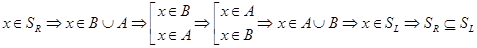 .
.
3) 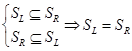 , т.е.
, т.е. 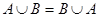 .
.
и. Пусть 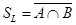 ,
, 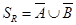 .
.
1) Докажем 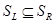 :
: 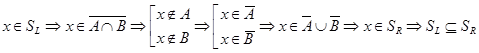 .
.
2) Докажем 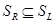 :
: 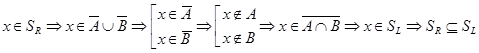 .
.
3) 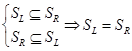 , т.е.
, т.е. 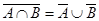 .
.
к. Пусть 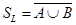 ,
, 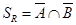 .
.
1) Докажем 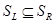 :
: 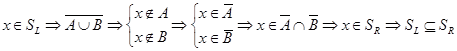 .
.
2) Докажем 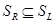 :
: 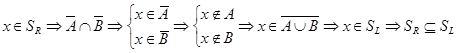 .
.
3) 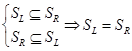 , т.е.
, т.е. 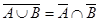 .
.
л. 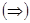 Пусть верно включение
Пусть верно включение 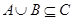 и элемент
и элемент 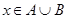 , тогда
, тогда
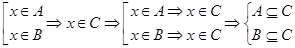 .
.
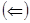 Пусть верны включения
Пусть верны включения 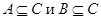 и элемент
и элемент 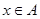 или
или 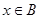 , тогда
, тогда
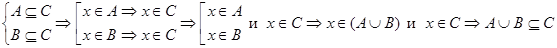 .
.
м. 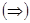 Пусть верно включение
Пусть верно включение 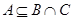 и элемент
и элемент 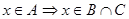 ,
, 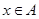
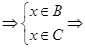
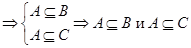 .
.
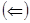 Пусть верны включения
Пусть верны включения 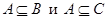 , тогда
, тогда 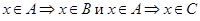 ,
, 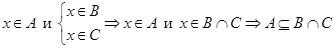 .
.
н. Пусть 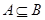 и
и 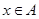 , при этом
, при этом 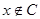 , тогда:
, тогда: 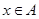
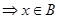 ,
, 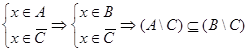 .
.
о. Пусть 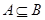 и
и 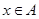 , при этом
, при этом 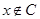 и
и 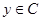 , тогда:
, тогда: 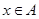
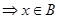 ,
, 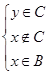
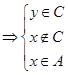 , но
, но 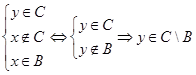 ,
, 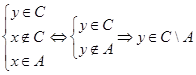 ,
, 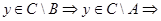
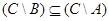 .
.
Задание 4.
а. 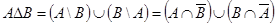
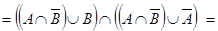
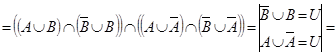
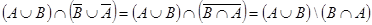 ,
,
что и требовалось доказать. Следует заметить, что равенство 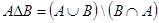 следует из Задания 2 в, так как является двойственным для доказанного там равенства.
следует из Задания 2 в, так как является двойственным для доказанного там равенства.
|
|
|
б. 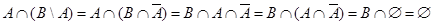 .
.
в. 1) 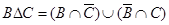 ,
, 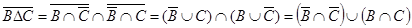 .
.
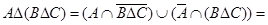
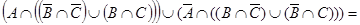
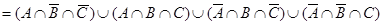 .
.
2) 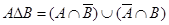 ,
, 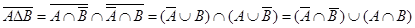 .
.
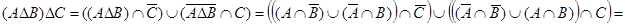
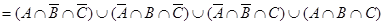
3) Из 1) и 2) пунктов видно, что 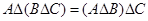 .
.
г. 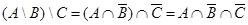 ,
, 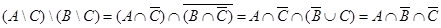 .
.
Видно, что 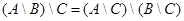 .
.
Задание 5.
а. 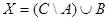 . б.
. б. 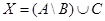 . в.
. в. 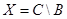 .
.
ПЗ 2. Отношения и функции
Задание 1.
а. 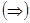 Пусть
Пусть 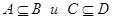 . Тогда любой элемент
. Тогда любой элемент 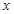 из A будет обязательно принадлежать и множеству B:
из A будет обязательно принадлежать и множеству B: 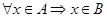 . То же можно сказать и об элементах множеств C и D:
. То же можно сказать и об элементах множеств C и D: 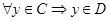 . Возьмем произвольный элемент декартова произведения
. Возьмем произвольный элемент декартова произведения 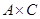 :
: 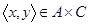 . Это значит (по определению), что
. Это значит (по определению), что 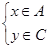 . Учитывая вложенность множеств A и B, C и D, имеем:
. Учитывая вложенность множеств A и B, C и D, имеем:
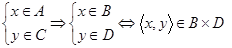 .
.
Отсюда следует вложение 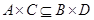 , что и требовалось доказать.
, что и требовалось доказать.
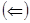 Путь
Путь 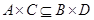 . Это значит, что
. Это значит, что 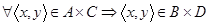 . Это можно записать следующим образом:
. Это можно записать следующим образом:
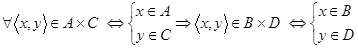 ,
,
то есть 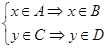 , откуда следуют доказываемые вложения
, откуда следуют доказываемые вложения 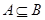 и
и 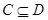 . Доказано.
. Доказано.
б. 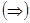 Пусть
Пусть 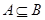 и
и 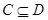 . Тогда очевидно, что
. Тогда очевидно, что 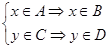 . Рассмотрим произвольную пару (элемент) из правой части доказываемого равенства, то есть
. Рассмотрим произвольную пару (элемент) из правой части доказываемого равенства, то есть 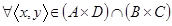 . Это значит, что
. Это значит, что
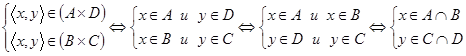 .
.
Ввиду вложений 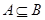 и
и 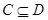 (а, следовательно, ввиду справедливости равенств
(а, следовательно, ввиду справедливости равенств 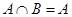 и
и 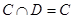 ) последнее утверждение эквивалентно следующему:
) последнее утверждение эквивалентно следующему: 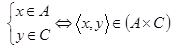 . Следовательно, имеет место вложение
. Следовательно, имеет место вложение 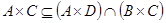 . Так как была построена цепочка эквивалентных утверждений (связанных знаком «
. Так как была построена цепочка эквивалентных утверждений (связанных знаком « 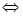 »), то справедливо и обратное вложение. Таким образом, равенство
»), то справедливо и обратное вложение. Таким образом, равенство 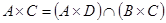 доказано.
доказано.
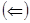 Пусть справедливо равенство
Пусть справедливо равенство 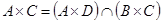 . Это значит, что
. Это значит, что
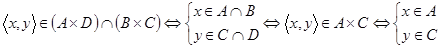 ,
,
то есть 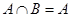 и
и 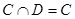 . Последнее возможно лишь в случае вложений
. Последнее возможно лишь в случае вложений 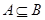 и
и 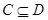 .
.
в. Обозначим 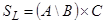 ,
, 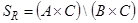 и докажем вложение
и докажем вложение 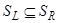 . Пусть
. Пусть 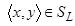 , тогда, по определению,
, тогда, по определению, 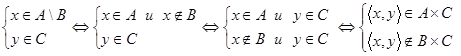
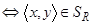 .
.
То есть справедливо вложение 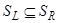 . Так как была построена цепочка эквивалентных утверждений (связанных знаком «
. Так как была построена цепочка эквивалентных утверждений (связанных знаком « 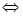 »), то справедливо и обратное вложение. Таким образом, равенство
»), то справедливо и обратное вложение. Таким образом, равенство 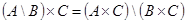 доказано.
доказано.
г. Пусть 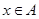 ,
, 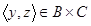 , т.е.
, т.е. 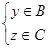 .. Тогда для
.. Тогда для 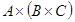 справедливо:
справедливо: 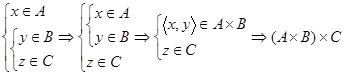 .
.
Для 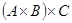 справедливо:
справедливо: 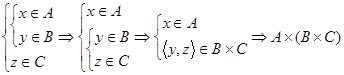 .
.
Таким образом 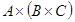 =
= 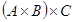 .
.
д. Обозначим 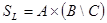 ,
, 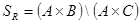 и докажем вложение
и докажем вложение 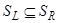 . Пусть
. Пусть 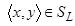 , тогда, по определению,
, тогда, по определению,
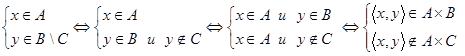
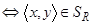 . То есть справедливо вложение
. То есть справедливо вложение 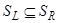 . Так как была построена цепочка эквивалентных утверждений (связанных знаком «
. Так как была построена цепочка эквивалентных утверждений (связанных знаком « 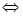 »), то справедливо и обратное вложение. Таким образом, равенство
»), то справедливо и обратное вложение. Таким образом, равенство 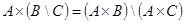 доказано.
доказано.
e. Обозначим 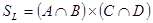 ,
, 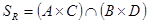 и докажем вложение
и докажем вложение 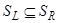 . Пусть
. Пусть 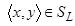 , тогда, по определению,
, тогда, по определению,
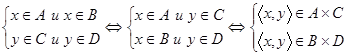
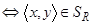 . То есть справедливо вложение
. То есть справедливо вложение 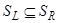 . Так как была построена цепочка эквивалентных утверждений (связанных знаком «
. Так как была построена цепочка эквивалентных утверждений (связанных знаком « 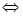 »), то справедливо и обратное вложение. Таким образом, равенство
»), то справедливо и обратное вложение. Таким образом, равенство 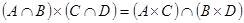 доказано.
доказано.
ж. Обозначим 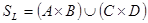 ,
, 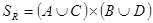 и докажем вложение
и докажем вложение 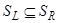 . Пусть
. Пусть 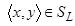 , тогда, по определению,
, тогда, по определению,
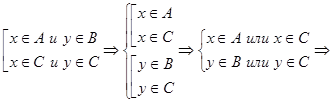
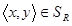 . То есть справедливо вложение
. То есть справедливо вложение 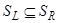 . Таким образом, вложение
. Таким образом, вложение 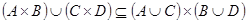 доказано.
доказано.
Задание 2.
а. Очевидно, Dr 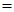 R, Rr
R, Rr 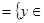 R
R 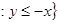 , графически это отношение можно изобразить как множество точек, расположенных ниже прямой
, графически это отношение можно изобразить как множество точек, расположенных ниже прямой 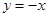 ;
;
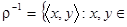 R
R 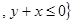
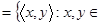 R
R 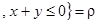 ;
;
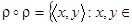 R:
R: 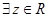 :
: 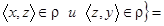
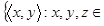 R
R 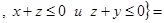
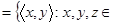 R
R 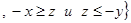 . Поскольку
. Поскольку 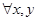 найдется такое z, что будут выполняться указанные неравенства, то
найдется такое z, что будут выполняться указанные неравенства, то 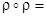 R2;
R2; 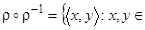 R
R 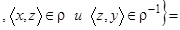
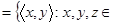 R
R 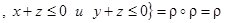 ;
; 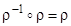 .
.
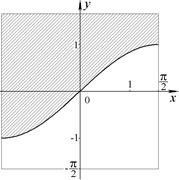 б. Чтобы обозначить область определения и область значений бинарного отношения
б. Чтобы обозначить область определения и область значений бинарного отношения 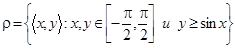 , обратимся к графическому изображению этого отношения.
, обратимся к графическому изображению этого отношения.
Из рисунка видно, что 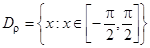 ,
, 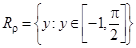 .
.
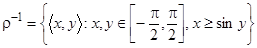 ;
;
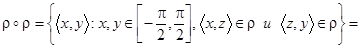
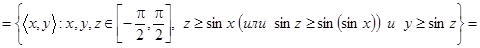
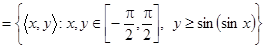 ;
;
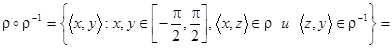
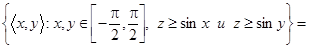
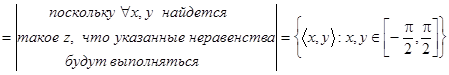 ;
;
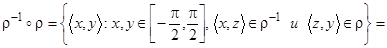
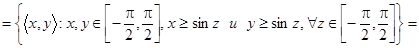
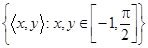 .
.
в. 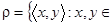 R
R 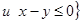 . Dr
. Dr 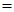 R, Rr
R, Rr 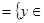 R
R 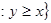 , графически это множество точек, расположенных выше прямой
, графически это множество точек, расположенных выше прямой 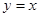 ;
; 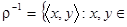 R
R 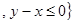 .
.
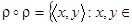 R:
R: 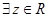 :
: 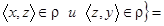
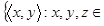 R
R 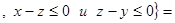
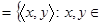 R
R 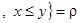 .
.
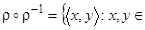 R,
R, 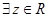 :
: 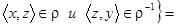
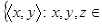 R
R 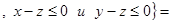
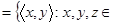 R
R 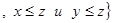 . Поскольку
. Поскольку 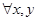 найдется такое z, что будут выполняться указанные неравенства, то
найдется такое z, что будут выполняться указанные неравенства, то 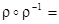 R2;
R2;
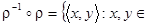 R:
R: 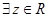 :
: 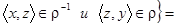
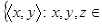 R
R 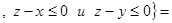
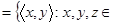 R
R 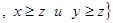 . Поскольку
. Поскольку 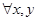 найдется такое z, что будут выполняться указанные неравенства, то
найдется такое z, что будут выполняться указанные неравенства, то 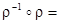 R2.
R2.
г. 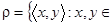 R
R 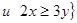 . Dr
. Dr 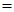 R, Rr
R, Rr 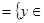 R
R 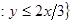 , графически это множество точек, расположенных ниже прямой
, графически это множество точек, расположенных ниже прямой 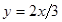 ;
; 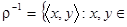 R
R 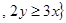 .
.
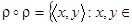 R:
R: 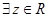 :
: 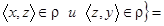
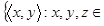 R
R 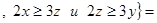
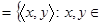 R
R 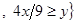 .
.
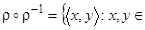 R,
R, 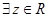 :
: 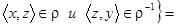
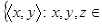 R
R 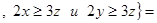
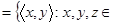 R
R 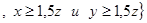 . Поскольку
. Поскольку 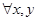 найдется такое z, что будут выполняться указанные неравенства, то
найдется такое z, что будут выполняться указанные неравенства, то 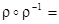 R2;
R2;
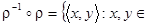 R:
R: 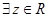 :
: 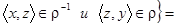
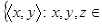 R
R 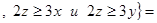
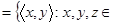 R
R 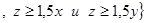 . Поскольку
. Поскольку 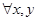 найдется такое z, что будут выполняться указанные неравенства, то
найдется такое z, что будут выполняться указанные неравенства, то 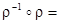 R2.
R2.
д. 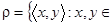 N
N 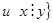 . Dr
. Dr 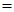 N, Rr
N, Rr 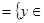 N
N 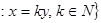 ,
, 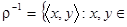 N
N 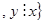 .
.
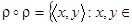 N:
N: 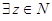 :
: 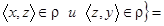
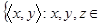 N
N 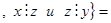
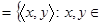 N
N 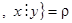 .
.
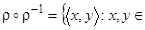 N,
N, 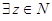 :
: 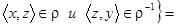
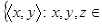 N
N 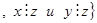 . Поскольку
. Поскольку 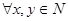 найдется такое
найдется такое 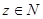 (в случае взаимно простых
(в случае взаимно простых 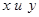 z=1), что будут выполняться указанные соотношения, то
z=1), что будут выполняться указанные соотношения, то 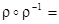 N2.
N2.
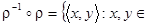 N:
N: 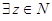 :
: 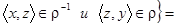
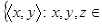 N
N 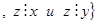 . Поскольку
. Поскольку 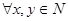 найдется такое
найдется такое 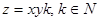 , что будут выполняться указанные соотношения, то
, что будут выполняться указанные соотношения, то 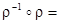 N2.
N2.
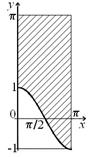
е. 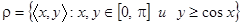 . Чтобы обозначить область определения и область значений бинарного отношения
. Чтобы обозначить область определения и область значений бинарного отношения 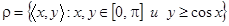 , обратимся к рисунку, из которого видно, что
, обратимся к рисунку, из которого видно, что 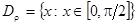 ,
, 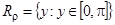 .
.
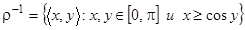 .
.
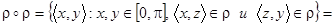
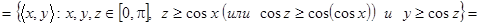
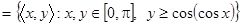 .
.
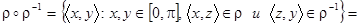
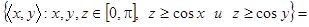
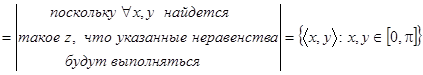 .
.
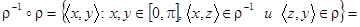
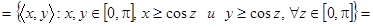
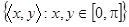 .
.
Задание 3.
а. Возьмем произвольный элемент отношения 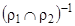 : пусть
: пусть 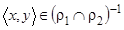 . По определению обратного отношения это означает, что пара
. По определению обратного отношения это означает, что пара
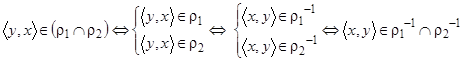 .
.
Таким образом, 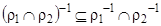 . Поскольку была построена цепочка эквивалентных утверждений (связанных знаком «
. Поскольку была построена цепочка эквивалентных утверждений (связанных знаком « 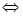 »), то справедливо и обратное вложение. Равенство доказано.
»), то справедливо и обратное вложение. Равенство доказано.
Замечание 1. Очевидно, что 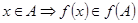 . Однако обратное утверждение в общем случае не верно: могут найтись
. Однако обратное утверждение в общем случае не верно: могут найтись 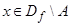 такие, что
такие, что 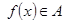 . Это происходит в случае не инъективных функций
. Это происходит в случае не инъективных функций 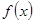 .
.
Замечание 2. Если отношение 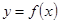 является функцией, то для обратного отношения
является функцией, то для обратного отношения 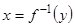 будет верно условие: если
будет верно условие: если 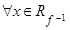 и
и 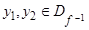 :
: 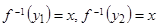 , то
, то 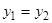 (в случае функциональности отношения
(в случае функциональности отношения 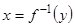 это будет означать его инъективность).
это будет означать его инъективность).
б. Пусть 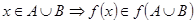 . Это эквивалентно тому, что
. Это эквивалентно тому, что 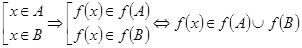 .
.
в. Пусть 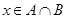 , тогда обязательно будет выполняться условие
, тогда обязательно будет выполняться условие 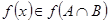 . С другой стороны,
. С другой стороны, 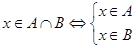 . Это значит, что
. Это значит, что 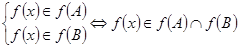 . Т.е. для любого элемента
. Т.е. для любого элемента 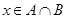 верно следующее:
верно следующее: 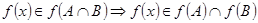 , что доказывает вложение
, что доказывает вложение 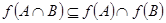 .
.
В качестве примера рассмотрим функцию 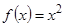 ,
, 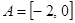 ,
, 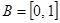 . Тогда
. Тогда 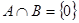 ,
, 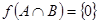 ,
, 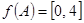 ,
, 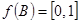 , следовательно
, следовательно 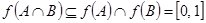 .
.
г. Поскольку 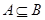 , то
, то 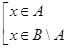 . В этом предположении надо доказать, что
. В этом предположении надо доказать, что 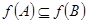 . По определению,
. По определению, 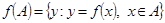 ,
, 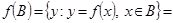
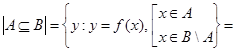
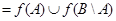 ,
, 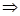
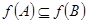 .
.
д. Поскольку 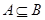 , то
, то 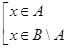 . В этом предположении надо доказать, что
. В этом предположении надо доказать, что 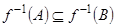 . Пусть
. Пусть 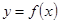 , тогда
, тогда 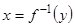 ,
, 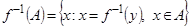 ,
, 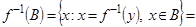
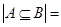
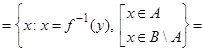
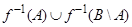 ,
, 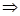
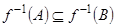 .
.
Задание 4.
Нужно показать рефлексивность, симметричность и транзитивность отношения 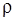 . Рефлексивность. Для любого элемента
. Рефлексивность. Для любого элемента 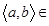 N
N 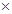 N должно выполняться
N должно выполняться 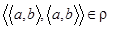 . Это так, поскольку верно равенство
. Это так, поскольку верно равенство 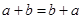 . Симметричность. Если
. Симметричность. Если 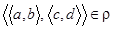 , то должно выполняться и
, то должно выполняться и 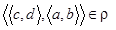 для любых элементов
для любых элементов 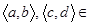 N
N 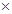 N. Действительно, если
N. Действительно, если 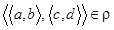 , то
, то 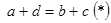 . Если же
. Если же 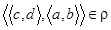 , то
, то 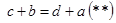 . Поскольку одновременно выполняются равенства
. Поскольку одновременно выполняются равенства 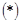 и
и 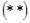 , то, очевидно, симметричность доказана. Транзитивность. Для любых элементов
, то, очевидно, симметричность доказана. Транзитивность. Для любых элементов 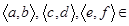 N
N 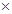 N при условии, что
N при условии, что 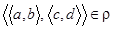 и
и 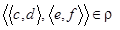 , должно выполняться
, должно выполняться 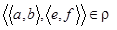 . По определению отношения
. По определению отношения 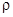 имеем:
имеем: 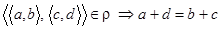 ;
; 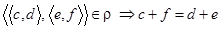 . Из равенства
. Из равенства 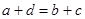 выразим
выразим 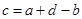 и подставим во второе равенство:
и подставим во второе равенство: 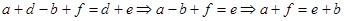 . Это, в свою очередь, означает, что
. Это, в свою очередь, означает, что 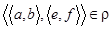 . Таким образом, отношение
. Таким образом, отношение 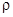 является отношением эквивалентности.
является отношением эквивалентности.
Задание 5.
а. рефлексивное, симметричное, транзитивное – отношение эквивалентности.
б. антирефлексивное, симметричное, антитранзитивное.
в. рефлексивное, симметричное, транзитивное – отношение эквивалентности.
г. рефлексивное, антисимметричное, транзитивное – отношение нестрогого частичного порядка, отношение нестрогого линейного порядка.
д. рефлексивное, антисимметричное, транзитивное – отношение нестрогого частичного порядка, отношение нестрогого линейного порядка.
е. антирефлексивное, строго антисимметричное, транзитивное – отношение строгого частичного порядка, отношение строгого линейного порядка.
ж. антирефлексивное, симметричное, нетранзитивное.
з. нерефлексивное, симметричное, нетранзитивное.
и. рефлексивное, симметричное, транзитивное – отношение эквивалентности.
ПЗ 3. Мощность множества
Задание 1.
а. Введем следующие множества:
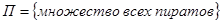 ;
; 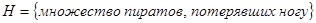 ;
; 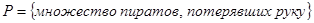 ;
; 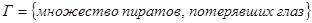 ;
; 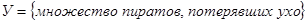 .
.
Поскольку в бою участвовало 100 пиратов, то 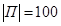 . Аналогично
. Аналогично 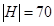 ,
, 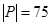 ,
, 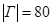 ,
, 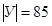 . Очевидно, что множество несчастных пиратов (обозначим его
. Очевидно, что множество несчастных пиратов (обозначим его 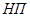 ), потерявших и ногу, и руку, и глаз, и ухо будет определяться пересечением
), потерявших и ногу, и руку, и глаз, и ухо будет определяться пересечением 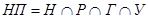 . Согласно принципу двойственности,
. Согласно принципу двойственности, 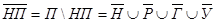 .
.
Очевидно, что 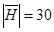 ,
, 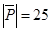 ,
, 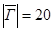 ,
,  . Тогда мощность множества
. Тогда мощность множества 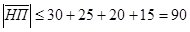 (знак
(знак 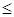 стоит потому, что один и тот же пират мог попасть в несколько из составляющих
стоит потому, что один и тот же пират мог попасть в несколько из составляющих 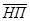 множеств одновременно).
множеств одновременно).
Таким образом, 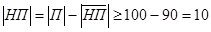 , то есть множество
, то есть множество 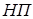 содержит как минимум 10 элементов, что и требовалось доказать.
содержит как минимум 10 элементов, что и требовалось доказать.
б. 501.Для решения задачи нужно найти мощность множества 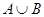 . Число полных периодов (расположенных подряд натуральных чисел, делящихся на 3 с остатком 1, 2, 0) при делении чисел от 1 до 1000 на 3 равно
. Число полных периодов (расположенных подряд натуральных чисел, делящихся на 3 с остатком 1, 2, 0) при делении чисел от 1 до 1000 на 3 равно 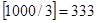 . Числа, образующие эти периоды, заканчиваются числом
. Числа, образующие эти периоды, заканчиваются числом 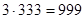 . Кроме того, есть числа, не образующие полный период (в данном случае это одно число - 1000, делящееся на 3 с остатком 1). Поэтому количество чисел делящихся на 3 с остатком 1 равно 333+1=334. Аналогично, количество чисел делящихся на 4 с остатком 3 равно
. Кроме того, есть числа, не образующие полный период (в данном случае это одно число - 1000, делящееся на 3 с остатком 1). Поэтому количество чисел делящихся на 3 с остатком 1 равно 333+1=334. Аналогично, количество чисел делящихся на 4 с остатком 3 равно 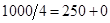 . Количество элементов объединения равно
. Количество элементов объединения равно 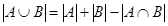 . В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 4 с остатком 3 (7, 19, 31, …), по одному числу из периода, образуемого при делении на
. В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 4 с остатком 3 (7, 19, 31, …), по одному числу из периода, образуемого при делении на 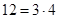 , т. е.
, т. е. 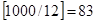 числа. Оставшиеся числа, не вошедшие в периоды: от
числа. Оставшиеся числа, не вошедшие в периоды: от 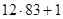 до
до 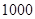 : 997, 998, 999, 1000. Ни одно из них условию не удовлетворяет. Итак,
: 997, 998, 999, 1000. Ни одно из них условию не удовлетворяет. Итак, 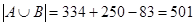 .
.
в. 57. Ищем мощность множества 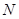 . Разложим на простые множители
. Разложим на простые множители 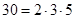 ,
, 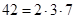 и
и 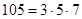 . Видно, что в множества
. Видно, что в множества 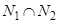 ,
, 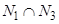 ,
, 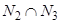 ,
, 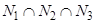 входят числа, нацело делящиеся на
входят числа, нацело делящиеся на 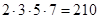 . Поскольку попарные пересечения множеств N1, N2 и N3 совпадают с их общим пересечением, то справедлива формула
. Поскольку попарные пересечения множеств N1, N2 и N3 совпадают с их общим пересечением, то справедлива формула
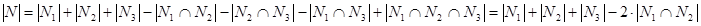 .
.
Аналогично задаче б, находим мощности множеств 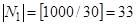 ,
, 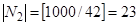 ,
, 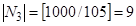 ,
, 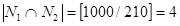 . Тогда
. Тогда 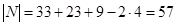 .
.
г. 86. В качестве универсального множества рассмотрим множество студентов первого, второго и третьего курсов. Обозначим M={множество студентов-юношей}, тогда 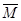 ={множество студенток}, A={множество первокурсников}, B={множество второкурсников} C={множество студентов третьего курса}. Первое условие задачи можно трактовать следующим образом: мощность дополнения множества студенток второго курса равна 347, т.е.
={множество студенток}, A={множество первокурсников}, B={множество второкурсников} C={множество студентов третьего курса}. Первое условие задачи можно трактовать следующим образом: мощность дополнения множества студенток второго курса равна 347, т.е. 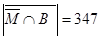 . Аналогично, второе условие: мощность дополнения множества студентов первого и второго курсов равна 125, то есть
. Аналогично, второе условие: мощность дополнения множества студентов первого и второго курсов равна 125, то есть 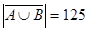 . Третье условие: мощность объединения множества первокурсников и множества студентов-юношей равна 308, или
. Третье условие: мощность объединения множества первокурсников и множества студентов-юношей равна 308, или 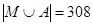 . Мощность универсального множества - общее количество студентов:
. Мощность универсального множества - общее количество студентов: 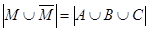 . Количество студентов-юношей третьего курса - мощность пересечения
. Количество студентов-юношей третьего курса - мощность пересечения 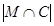 .
.
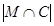 - количество студентов-юношей третьего курса - можно посчитать как разность общего количества студентов третьего курса и количества студенток третьего курса:
- количество студентов-юношей третьего курса - можно посчитать как разность общего количества студентов третьего курса и количества студенток третьего курса: 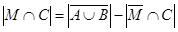 . Преобразуем условия задачи:
. Преобразуем условия задачи: 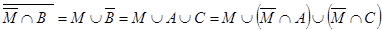 , поэтому
, поэтому
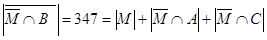 ;
; 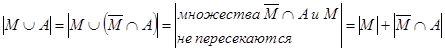 ,
,
поэтому 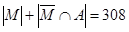 , то есть
, то есть 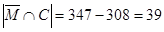 . Последнее означает, что на третьем курсе обучаются 39 девушек. Общее количество студентов третьего курса, по условию, равно
. Последнее означает, что на третьем курсе обучаются 39 девушек. Общее количество студентов третьего курса, по условию, равно 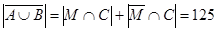 , а значит, количество юношей, обучающихся на третьем курсе, равно
, а значит, количество юношей, обучающихся на третьем курсе, равно 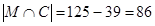 .
.
д. Решение задачи аналогично заданию 1 б, откуда известно, что 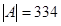 . Найдем
. Найдем 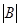 и
и 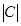 .
. 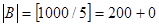 ,
, 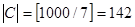 . Числа, образующие периоды при делении на 7, заканчиваются числом
. Числа, образующие периоды при делении на 7, заканчиваются числом 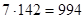 . Кроме того, есть числа, не образующие полный период (в данном случае это одно число - 998, делящееся на 7 с остатком 4). Поэтому количество чисел делящихся на 7 с остатком 4 равно 142+1=143.
. Кроме того, есть числа, не образующие полный период (в данном случае это одно число - 998, делящееся на 7 с остатком 4). Поэтому количество чисел делящихся на 7 с остатком 4 равно 142+1=143.
1) Найдем 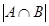 . В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 5 с остатком 2 (7, 22, 37, …), по одному числу из периода, образуемого при делении на
. В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 5 с остатком 2 (7, 22, 37, …), по одному числу из периода, образуемого при делении на 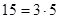 , т. е.
, т. е.  чисел. Оставшиеся числа, не вошедшие в периоды: от
чисел. Оставшиеся числа, не вошедшие в периоды: от 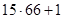 до
до 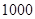 : 991, ..., 1000. Только одно из них удовлетворяет условию: 997. Итак,
: 991, ..., 1000. Только одно из них удовлетворяет условию: 997. Итак, 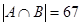 .
.
2) 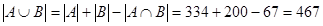 .
.
3) 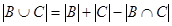 . Найдем
. Найдем 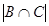 . В пересечение входят числа, одновременно делящиеся на 5 с остатком 2 и на 7 с остатком 4 (32, 67, 102, …), по одному числу из периода, образуемого при делении на
. В пересечение входят числа, одновременно делящиеся на 5 с остатком 2 и на 7 с остатком 4 (32, 67, 102, …), по одному числу из периода, образуемого при делении на 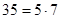 , т. е.
, т. е. 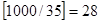 чисел. Оставшиеся числа, не вошедшие в периоды: от
чисел. Оставшиеся числа, не вошедшие в периоды: от 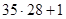 до
до 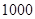 : 981, ..., 1000. Ни одно из них не удовлетворяет условию. Итак,
: 981, ..., 1000. Ни одно из них не удовлетворяет условию. Итак,
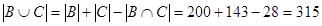 .
.
4) 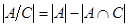 . Найдем
. Найдем 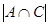 . В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 7 с остатком 4 (4, 25, 46, …), по одному числу из периода, образуемого при делении на
. В пересечение входят числа, одновременно делящиеся на 3 с остатком 1 и на 7 с остатком 4 (4, 25, 46, …), по одному числу из периода, образуемого при делении на 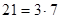 , т. е.
, т. е. 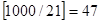 чисел. Оставшиеся числа, не вошедшие в периоды: от
чисел. Оставшиеся числа, не вошедшие в периоды: от 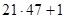 до
до 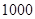 : 988, ..., 1000. Только одно из них удовлетворяет условию: 991. Итак,
: 988, ..., 1000. Только одно из них удовлетворяет условию: 991. Итак, 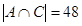
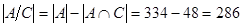 .
.
е. Для начала выпишем условия задачи из 1 в:
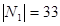 ,
, 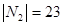 ,
, 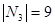 ,
, 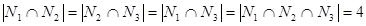 .
.
1) 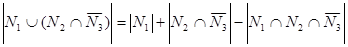 . При пересечении множеств
. При пересечении множеств 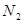 и
и 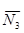 , исключаются все элементы множества
, исключаются все элементы множества 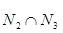 . Т.к.
. Т.к. 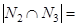 4, то количество элементов
4, то количество элементов 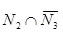 равно выражению
равно выражению 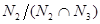 =
= 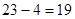 . Т.к.
. Т.к. 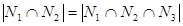 , то
, то 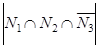 =0.
=0.
Тогда 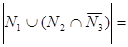
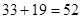 .
.
2) 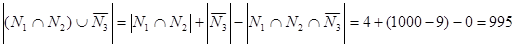 .
.
3) 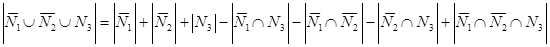 =
=
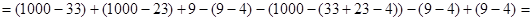 1000.
1000.
4) 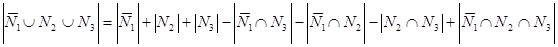 =
=
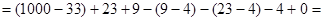 971.
971.
ж. Пусть дома будут обозначаться условно 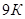 ,
, 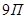 ,
, 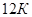 ,
, 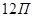 ,
, 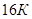 ,
, 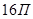 . Выпишем данные:
. Выпишем данные: 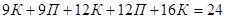 ,
, 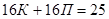 ,
, 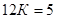 ,
, 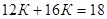 . Найдем
. Найдем 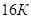 :
: 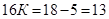 , и
, и 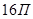 :
: 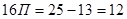 . Тогда
. Тогда 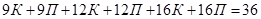 . Таким образом, в микрорайоне «Высотный» построено 36 домов.
. Таким образом, в микрорайоне «Высотный» построено 36 домов.
з. Составим систему уравнений. Пусть спортсмены-мужчины будут обозначаться условно 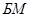 ,
, 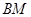 и
и 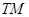 , девушки-спортсменки соответственно
, девушки-спортсменки соответственно 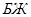 ,
, 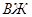 и
и 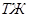 . Получаем систему:
. Получаем систему:
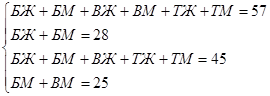
Решаем систему уравнений. Видно, что из первого уравнения можно вычесть третье. Таким образом, мы найдем количество волейболистов-мужчин: 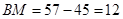 . Подставляем
. Подставляем 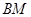 в последнее уравнение:
в последнее уравнение: 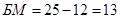 . Полученный результат подставим во второе уравнение:
. Полученный результат подставим во второе уравнение: 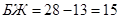 . Таким образом, в «Чемпионе» 15 женщин занимаются баскетболом.
. Таким образом, в «Чемпионе» 15 женщин занимаются баскетболом.
Задание 2.
а. Множество (0,1) - бесконечно. Справедливо утверждение: мощность бесконечного множества не изменится, если к нему прибавить (или удалить из него) конечное число элементов. Таким образом, 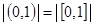 . Теперь докажем равномощность этих множеств по определению. Т.е. необходимо построить взаимно однозначное соответствие (биекцию) между элементами [0,1]и(0,1). Обозначим
. Теперь докажем равномощность этих множеств по определению. Т.е. необходимо построить взаимно однозначное соответствие (биекцию) между элементами [0,1]и(0,1). Обозначим 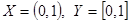 . Выделим следующие счетные подмножества из множеств X и Y:
. Выделим следующие счетные подмножества из множеств X и Y:
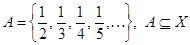 ,
, 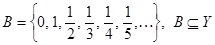 . Сопоставим элементы полученных множеств:
. Сопоставим элементы полученных множеств: 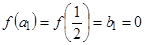 ,
, 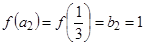 ,
, 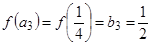 ,
, 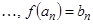 . Искомую биекцию можно организовать следующим образом:
. Искомую биекцию можно организовать следующим образом:
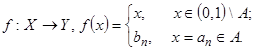 Равномощность множеств X и Y доказана.
Равномощность множеств X и Y доказана.
б. Искомое отображение будем строить в два этапа. 1. 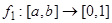 . Пусть
. Пусть 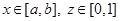 , тогда функцию
, тогда функцию 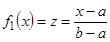 можно взять в качестве биекции, отображающей отрезок
можно взять в качестве биекции, отображающей отрезок 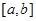 на
на 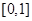 .
.
2. 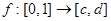 . Пусть
. Пусть 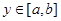 , тогда
, тогда 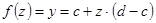 . Следовательно, искомое отображение будет следующим:
. Следовательно, искомое отображение будет следующим: 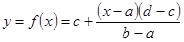 .
.
в. Необходимо построить отображение f такое, что 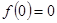 ,
, 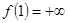 . То есть
. То есть 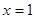 - точка разрыва второго рода для функции
- точка разрыва второго рода для функции 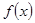 . Таким образом, искомое отображение можно описать следующей функцией:
. Таким образом, искомое отображение можно описать следующей функцией: 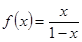 .
.
г. В качестве искомой биекции можно использовать любую монотонную (биективную) функцию 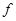 , имеющую область значений
, имеющую область значений 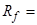 R. Возьмем одну ветвь функции
R. Возьмем одну ветвь функции 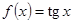 . Однако для этого аргумент должен изменяться на интервале
. Однако для этого аргумент должен изменяться на интервале 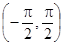 . Поэтому необходимо построить дополнительное отображение
. Поэтому необходимо построить дополнительное отображение 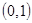 на
на 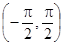 . Используя формулу из пункта б, имеем:
. Используя формулу из пункта б, имеем: 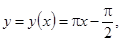 где
где 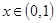 ,
, 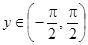 . Таким образом, искомое отображение
. Таким образом, искомое отображение 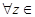 R
R 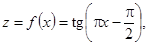
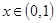 .
.
д. В качестве биекции можно использовать любую строго монотонную функцию. В данном случае можно воспользоваться функцией 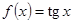 : эта функция определена для
: эта функция определена для 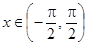 , при этом
, при этом 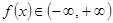 . Т.е., достаточно сначала построить биекцию
. Т.е., достаточно сначала построить биекцию 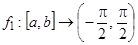 ,
, 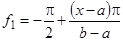 , затем выразить искомое отображение
, затем выразить искомое отображение 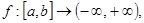
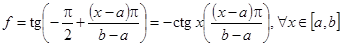 .
.
е. Равномощность множеств (0,1), [0,1) и (0,1] доказывается подобно пункту а, т.е. необходимо построить взаимно однозначное соответствие между элементами [0,1)и(0,1); (0,1] и (0,1).
ж. Необходимо построить отображение f такое, что 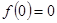 ,
, 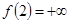 . То есть
. То есть  - точка разрыва второго рода для функции
- точка разрыва второго рода для функции 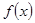 . Таким образом, искомое отображение:
. Таким образом, искомое отображение: 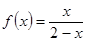 .
.
з. Искомое отображение: 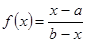 .
.
и. Искомое отображение: 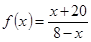 .
.
к. Искомое отображение: 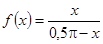 .
.
л. Искомое отображение: 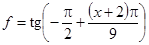 .
.
м. Искомое отображение: 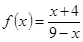 .
.
ПЗ 4. Элементы комбинаторики
1. 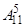 . 2. 42. 3.
. 2. 42. 3. 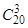 . 4. 968. 5. 253. 6. 64. 7. 240. 8. 124. 9.
. 4. 968. 5. 253. 6. 64. 7. 240. 8. 124. 9. 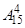 . 10.
. 10. 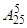 . 11.
. 11. 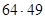 . 12.
. 12. 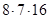 . 13. 8!. 14. 30!/(10!)3. 15. 42. 16. 9!. 17.
. 13. 8!. 14. 30!/(10!)3. 15. 42. 16. 9!. 17. 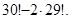 18.
18. 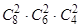 . 19. 12!/(2!)6. 20. 204. 21. 2×9!. 22.
. 19. 12!/(2!)6. 20. 204. 21. 2×9!. 22. 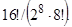 . 23. 56; 6×45. 24. 210. 25. 16100. 26. 40. 27. 80!/(3! ×75!). 28. 10!/48. 29. 36; 6!. 30. 44×32. 31.
. 23. 56; 6×45. 24. 210. 25. 16100. 26. 40. 27. 80!/(3! ×75!). 28. 10!/48. 29. 36; 6!. 30. 44×32. 31. 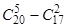 . 32.
. 32. 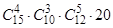 . 33.
. 33. 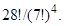 34.
34. 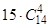 . 35. 35. 36. 108. 37. 16!/(26×32). 38. 420. 39.
. 35. 35. 36. 108. 37. 16!/(26×32). 38. 420. 39. 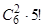 . 40.
. 40. 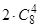 . 41. 62. 42. 9×106. 43.
. 41. 62. 42. 9×106. 43. 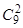 . 44. 60. 45. 2(6!)2. 46. 2200. 47. 86; 86–13×75. 48. 2(11!)2. 49. Пусть х – количество книг по логике, тогда (20–x) – по математике. Количество вариантов комплекта, содержащего 5 книг по логике и 5 по математике:
. 44. 60. 45. 2(6!)2. 46. 2200. 47. 86; 86–13×75. 48. 2(11!)2. 49. Пусть х – количество книг по логике, тогда (20–x) – по математике. Количество вариантов комплекта, содержащего 5 книг по логике и 5 по математике: 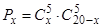 . Чтобы найти max
. Чтобы найти max 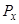 , сравним отношение двух последовательных значений
, сравним отношение двух последовательных значений 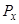 и
и 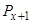 с единицей. Если
с единицей. Если 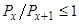 , то
, то 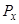 возрастает, если
возрастает, если 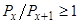 , то
, то 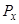 убывает; надо найти такое х, при которых возрастающая последовательность станет убывающей.
убывает; надо найти такое х, при которых возрастающая последовательность станет убывающей. 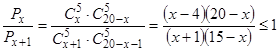 ,
, 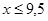 . При х=9 последовательность возрастает, при х=10 – убывает, поэтому искомое х=10. 50. Количество способов распределить пассажиров по группам:
. При х=9 последовательность возрастает, при х=10 – убывает, поэтому искомое х=10. 50. Количество способов распределить пассажиров по группам: 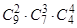 . Каждая из групп может выйти на любом из девяти этажей:
. Каждая из групп может выйти на любом из девяти этажей: 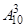 . Тогда
. Тогда 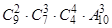 =10!/4.
=10!/4.
ПЗ 9. Изоморфизм графов
Задание 1.
а. Таких графов 11.
б. Таких графов 2.
в. 1) Таких графов 3.
2) Таких графов 9.
3) Таких графов 5 (6?).
г. Таких графов 1) 2; 2) 2; 3) 0.
Задание 2.
а. Таких графов 1) ; 2) 4; 3) ; 4) 3.
б. 5.
в.
г. Пусть у графа N вершин. Их степени могут быть числами 0, 1, N-1 (всего N вариантов) Предположим, что вершин с одинаковыми степенями нет. Тогда очевидно, что есть вершина A со степенью 0 (изолированная) и вершина B со степенью N-1 (смежная со всеми остальными, в том числе и с A). Но A не может быть ни с кем смежна. Противоречие.
д. Удобнее строить дополнения графов. 1) 9 графов; 2) 11 графов; 3) 5 графов.
Задание 3.
Рис. 1,3,4,5,7 пары изоморфных графов.
ПЗ 10. Гомеоморфизм графов
Задание 1.
1) В каждом из графов, изображенных на рис. 9, существует подграф, гомеоморфный K4.
2) В графе на рис. 9, б естьподграф, гомеоморфный К5. В графе на рис. 9, б существуетподграф, гомеоморфный К2,3.
Задание 2.
Все гомеоморфны.
ПЗ 12. Полином Жегалкина, линейность, самодвойственность функций
Задание 6. а. 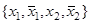 б.
б. 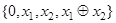 . в.
. в. 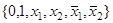 . г.
. г. 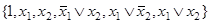 .
.
Задание 7. а. 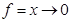 б.
б. 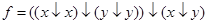 . в.
. в. 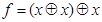 . г.
. г. 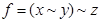 . д.
. д. 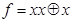 . е.
. е. 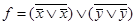 .
.
Элементы теории множеств
| № варианта | № задания | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 2 | 3 | собственное | 1 | 1,3 | 4 | 2 | 3 | 1 | 3 |
| 2 | 4 | 4 | пустое | 3 | 2,3,4 | 3 | 4 | 2 | 2 | 1 |
| 3 | 2 | 1 | Î | 2 | 1,2 | 4 | 1 | 1 | 3 | 3 |
| 4 | 3 | 2 | Î | 3 | 2,3 | 3 | 3 | 3 | 1 | 4 |
| 5 | 4 | 2 | Ï | 3 | 2,3,4 | 2 | 4 | 2 | 2 | 2 |
| 6 | 1 | 4 | {2,3} | 1 | 2,4 | 3 | 1 | 4 | 3 | 1 |
| 7 | 3 | 1 | Æ | 2 | 1,2,4 | 1 | 3 | 2 | 2 | 4 |
| 8 | 2 | 4 | 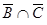
| 2 | 1,3,5,6 | 4 | 4 | 1 | 1 | 1 |
| 9 | 4 | 2 | 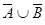
| 3 | 2,3,4,6 | 3 | 2 | 3 | 3 | 1 |
| 10 | 2 | 1 | A | 2 | 1,4 | 2 | 3 | 2 | 3 | 3 |
| 11 | 1 | 2 | A | 1 | 2,3 | 1 | 1 | 1 | 1 | 2 |
| 12 | 4 | 3 | (AÈB)Ç(AÈC) | 2 | 1,3 | 4 | 3 | 3 | 4 | 3 |
| 13 | 3 | 4 | (AÇB)È(AÇC) | 2 | 2,3 | 3 | 2 | 2 | 2 | 1 |
| 14 | 2 | 1 | A | 3 | 1,2,3 | 4 | 3 | 1 | 2 | 1 |
| 15 | 4 | 2 | U | 2 | 2,3 | 1 | 4 | 2 | 4 | 4 |
| 16 | 3 | 3 | A | 1 | 1,2,3 | 2 | 2 | 4 | 2 | 3 |
| 17 | 1 | 4 | U | 4 | 2,5,6 | 4 | 4 | 3 | 1 | 2 |
| 18 | 3 | 1 | Æ | 3 | 2,3,5 | 2 | 1 | 1 | 2 | 3 |
| 19 | 2 | 2 | A | 4 | 2,3,5,6 | 4 | 3 | 4 | 1 | 4 |
| 20 | 1 | 2 | Æ | 3 | 2,3 | 4 | 4 | 3 | 3 | 1 |
| 21 | 4 | 1 | {1,2,3}{2,4} | 1 | 1,3,4 | 3 | 3 | 4 | 4 | 2 |
| 22 | 3 | 4 | {1,3,5,7}{2,3,5} | 3 | 2,3,4 | 4 | 1 | 2 | 2 | 2 |
| 23 | 1 | 3 | <1,x> | 4 | 2,3 | 1 | 4 | 1 | 1 | 4 |
| 24 | 2 | 4 | <2,1> | 2 | 1,3 | 3 | 2 | 3 | 3 | 3 |
| 25 | 4 | 1 | 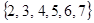
| 3 | 1,2 | 3 | 3 | 1 | 3 | 1 |
| 26 | 4 | 2 | 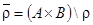
| 2 | 1,3 | 1 | 2 | 4 | 4 | 4 |
| 27 | 3 | 3 | 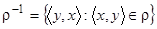
| 1 | 1,3 | 2 | 4 | 3 | 1 | 3 |
| 28 | 4 | 2 | предпорядком на A | 2 | 1,2,3 | 2 | 1 | 1 | 2 | 1 |
| 29 | 2 | 3 | строгого частичного порядка | 4 | 1,3,5, 6 | 4 | 3 | 2 | 3 | 2 |
| 30 | 2 | 1 | линейного порядка | 1 | 3,5,6 | 1 | 2 | 1 | 3 | 3 |
Элементы теории графов
| № варианта | № задания | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 1 | инцидентно | 1 | 2 | 3 | 1 | 4 | 3 | 2 |
| 2 | 2 | 2 | смежными | 2 | 1 | 1 | 3 | 3 | 2 | 1 |
| 3 | 3 | 4 | маршрутом | 4 | 3 | 4 | 1 | 2 | 1 | 3 |
| 4 | 4 | 4 | путем | 3 | 4 | 3 | 2 | 1 | 3 | 1 |
| 5 | 3 | 4 | Эйлеровой | 2 | 3 | 1 | 1 | 2 | 1 | 2 |
| 6 | 1 | 4 | Эйлеровым | 1 | 1 | 1 | 2 | 3 | 2 | 4 |
| 7 | 2 | 1 | Эйлеровым | 2 | 4 | 3 | 4 | 3 | 4 | 3 |
| 8 | 4 | 4 | длиной маршрута | 4 | 2 | 2 | 1 | 1 | 1 | 2 |
| 9 | 1 | 4 | длиной пути | 2 | 4 | 1 | 4 | 2 | 4 | 1 |
| 10 | 2 | 3 | четными | 3 | 1 | 2 | 3 | 3 | 3 | 2 |
| 11 | 1 | 3 | 2 | 1 | 3 | 3 | 2 | 1 | 4 | 3 |
| 12 | 2 | 1 | подграфом | 3 | 2 | 2 | 1 | 2 | 1 | 1 |
| 13 | 1 | 4 | собственным | 2 | 1 | 2 | 4 | 2 | 2 | 2 |
| 14 | 2 | 3 | достижима | 1 | 3 | 1 | 1 | 2 | 3 | 3 |
| 15 | 1 | 2 | связным | 3 | 2 | 2 | 1 | 2 | 3 | 1 |
| 16 | 3 | 4 | сильно связным | 1 | 3 | 4 | 3 | 2 | 4 | 2 |
| 17 | 2 | 1 | связным | 2 | 1 | 4 | 4 | 4 | 1 | 4 |
| 18 | 3 | 4 | компонентой связности | 1 | 4 | 3 | 2 | 2 | 4 | 3 |
| 19 | 4 | 3 | компонентой сильной связности | 4 | 2 | 4 | 1 | 2 | 1 | 2 |
| 20 | 4 | 1 | расстоянием | 1 | 1 | 1 | 4 | 3 | 2 | 1 |
| 21 | 4 | 1 | диаметром | 2 | 2 | 1 | 4 | 3 | 2 | 2 |
| 22 | 3 | 2 | максимальным удалением (эксцентриситетом) | 1 | 2 | 4 | 2 | 2 | 2 | 3 |
| 23 | 1 | 4 | радиусом | 3 | 3 | 1 | 3 | 2 | 4 | 4 |
| 24 | 2 | 3 | центром | 1 | 4 | 4 | 1 | 2 | 4 | 1 |
| 25 | 2 | 4 | нагруженный | 2 | 2 | 4 | 3 | 1 | 4 | 2 |
| 26 | 2 | 4 | гамильтонов | 3 | 4 | 3 | 3 | 2 | 3 | 2 |
| 27 | 4 | 2 | простой цепью | 2 | 2 | 3 | 2 | 4 | 1 | 1 |
| 28 | 2 | 2 | минимальным | 3 | 3 | 2 | 2 | 3 | 2 | 4 |
| 29 | 2 | 1 | простую цепь | 4 | 4 | 1 | 3 | 4 | 1 | 2 |
| 30 | 3 | 3 | полным двудольным | 2 | 3 | 1 | 3 | 3 | 4 | 3 |
Элементы алгебры логики
| № вар. | № задания | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | Булевым (двоичным) набором | 3 | 3 | 2 | 1 | 1 | 2 | 2 | 1 | 1 | 4 |
| 2 | предшествует (или не больше) | 2 | 1 | 4 | 2 | 3 | 3 | 1 | 2 | 4 | 3 |
| 3 | расстоянием Хемминга | 1 | 4 | 4 | 3 | 1 | 4 | 3 | 3 | 2 | 1 |
| 4 | соседними | 4 | 1 | 1 | 3 | 3 | 4 | 3 | 1 | 2 | 2 |
| 5 | противоположными | 1 | 3 | 2 | 4 | 2 | 1 | 3 | 4 | 1 | 3 |
| 6 | сравнимыми | 3 | 3 | 1 | 2 | 2 | 2 | 2 | 4 | 4 | 2 |
| 7 | частичного порядка | 2 | 1 | 3 | 1 | 3 | 3 | 4 | 2 | 2 | 1 |
| 8 | функцией алгебры логики (булевой функцией) | 1 | 3 | 3 | 4 | 4 | 1 | 2 | 1 | 4 | 4 |
| 9 | ноль-местной | 4 | 1 | 2 | 2 | 4 | 3 | 1 | 3 | 4 | 1 |
| 10 | конъюнкцией | 3 | 2 | 3 | 4 | 1 | 2 | 2 | 2 | 3 | 2 |
| 11 | одноместной | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 3 | 2 | 2 |
| 12 | дизъюнкцией | 2 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 3 | 4 |
| 13 | сложением по модулю 2 | 2 | 3 | 3 | 1 | 3 | 3 | 1 | 3 | 2 | 3 |
| 14 | эквиваленцией | 2 | 1 | 1 | 2 | 1 | 2 | 1 | 2 | 3 | 4 |
| 15 | импликацией | 1 | 1 | 2 | 3 | 2 | 1 | 2 | 1 | 2 | 3 |
| 16 | штрихом Шеффера | 3 | 2 | 3 | 1 | 3 | 2 | 1 | 3 | 3 | 4 |
| 17 | стрелкой Пирса (функцией Вебба) | 1 | 2 | 4 | 2 | 1 | 3 | 2 | 2 | 1 | 4 |
| 18 | отрицание | 3 | 3 | 1 | 2 | 2 | 2 | 1 | 1 | 2 | 2 |
| 19 | отрицание и конъюнкция | 3 | 3 | 2 | 4 | 2 | 2 | 2 | 2 | 3 | 4 |
| 20 | существенным образом | 1 | 2 | 3 | 2 | 2 | 2 | 3 | 3 | 2 | 2 |
| 21 | фиктивной переменной | 4 | 4 | 1 | 3 | 1 | 3 | 1 | 1 | 1 | 2 |
| 22 | равными | 1 | 3 | 2 | 1 | 1 | 2 | 4 | 3 | 2 | 3 |
| 23 | формулой (отрицанием) | 3 | 3 | 1 | 2 | 3 | 1 | 2 | 2 | 1 | 3 |
| 24 | ассоциативностью | 3 | 2 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 1 |
| 25 | дистрибутивностью | 1 | 4 | 4 | 2 | 3 | 3 | 3 | 2 | 2 | 3 |
| 26 | базисом | 1 | 4 | 3 | 2 | 1 | 1 | 2 | 2 | 2 | 4 |
| 27 | T1 | 2 | 4 | 2 | 3 | 2 | 4 | 1 | 3 | 2 | 1 |
| 28 | M | 2 | 2 | 4 | 2 | 2 | 3 | 2 | 3 | 1 | 3 |
| 29 |  (штрих Шеффера, стрелка Пирса) (штрих Шеффера, стрелка Пирса)
| 1 | 4 | 1 | 2 | 1 | 2 | 1 | 3 | 3 | 1 |
| 30 | x, 0, 1 | 2 | 4 | 2 | 2 | 2 | 1 | 3 | 1 | 3 | 2 |
Дата добавления: 2021-03-18; просмотров: 108; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
