Закон Ома для неоднородного участка цепи
Если под действием электрического поля 
в проводнике возникает ток плотности 
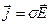, то очевидно, что при совместном действии поля и поля сторонних сил 
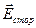плотность тока:
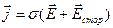. (5.17)
Рассмотрим цилиндрический проводник с площадью поперечного сечения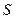 
и длиной 
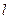. Умножим (5.17) на перемещение 
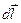вдоль оси проводника и проинтегрируем, по длине проводника от 0 до 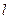. В результате получим:
,
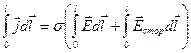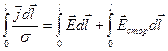
или
.
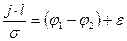Преобразуем выражение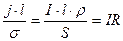 
.
Следовательно,
или
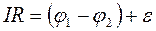. (5.18)
Формулы (5.18) выражает закон Ома для неоднородного участка проводника.
Рассмотрим неоднородный участок цепи (рис.5.8).
Рис.5.8
Сила тока положительна, когда ток течет от точки 1 к точке 2. ЭДС считается положительной, если она способствует движению положительных носителей в направлении 1-2 (т.е. направление тока совпадает с направлением 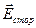внутри источника тока.
Таким образом,
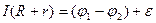, (5.19)
где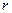 
- внутреннее сопротивление источника тока.
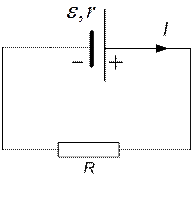
Для замкнутой цепи (рис.5.9)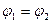 
, закон Ома имеет вид:
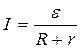. (5.20)
Отсюда
, 
,
где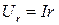 
- падение напряжения на внутреннем сопротивлении источника тока, 
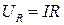- напряжение на внешнем сопротивлении.
|
|
|
Рис.5.9
Закон Джоуля - Ленца
Проводник при прохождении по нему тока нагревается. Джоуль и независимо от него Ленц установили экспериментально, что количество выделившейся в проводнике теплоты пропорционально его сопротивлению, квадрату силы тока и времени:
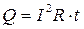. (5.21)
Эта формула выражает закон Джоуля – Ленца. С учетом закона Ома (5.14)
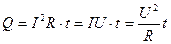, (5.22)
где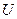 
- напряжение между концами проводника.
Формулы (5.22) справедливы для постоянного тока (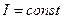 
). Если сила тока зависит от времени, то закон Джоуля-Ленца можно записать в интегральной форме:
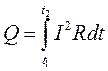. (5.22а)
Рассмотрим, как в параграфе 5.4, однородный цилиндрический проводник с площадью поперечного сечения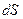 
и длиной 
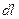(рис.5.7). Тогда на основании закона Джоуля - Ленца в этом объеме за время 
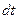выделяется количество теплоты:
,
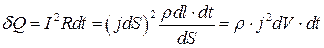где 
.
Разделив это уравнение на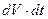 
, получим формулу, которая определяет количество теплоты, выделяемое в единице объема в единицу времени – удельную тепловую мощность тока:
|
|
|
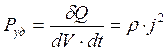. (5.23)
Эта формула выражает закон Джоуля –Ленца в дифференциальной форме: удельная тепловая мощность тока пропорциональна квадрату плотности тока и удельному сопротивлению среды в данной точке.
Приняв во внимание соотношение (5.16) для закона Ома, формулу (5.23) можно представить в виде:
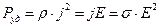. (5.24)
Правила Кирхгофа для расчета разветвленных электрических цепей
В основе расчета лежат два правила Кирхгофа.
Первое правило Кирхгофа – оно относится к узлам цепи, т.е. к точкам ее разветвления: алгебраическая сумма токов, сходящихся в узле, равна нулю:
. (5.25)
Току, текущему к узлу, приписывается один знак, скажем плюс, току, текущему от узла, - другой знак (тогда минус). Например, для рис.5.10 уравнение (5.25) запишется так:
.
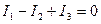Уравнение (5.25) есть следствие закона сохранения электрического заряда.
Уравнение (5.25) можно написать для всех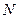 
узлов. Однако независимыми будут только 
уравнение, 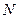-тое будет следствием остальных.
|
|
|
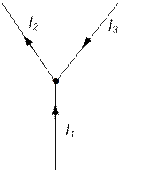
Рис.5.10
Рис.5.11
Второе правило Кирхгофа – оно относится к любому выделенному в разветвленной цепи замкнутому контуру: алгебраическая сумма произведений сил тока на сопротивления отдельных участков контура равна алгебраической сумме ЭДС, действующих в этом замкнутом контуре:
. (5.26)
Если в разветвленной цепи можно выделить несколько замкнутых контуров, то независимые уравнения (5.26) можно составить только для тех контуров, которые не получаются в результате наложения уже рассмотренных. Например, для цепи (рис.5.11) такие уравнения для контуров 124 и 234 будут независимыми. Уравнение для контура 1234 является следствием двух предыдущих.
При составлении уравнений (5.25) и (5.26) необходимо поступать так.
1. Выбрать произвольно направления токов и направления обхода контура.
2. Если выбранное направление тока совпадает с направлением обхода, то соответствующее слагаемое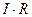 
надо брать со знаком плюс, если же эти направления противоположны, то со знаком минус. ЭДС также нужно брать со знаком плюс, если ЭДС повышает потенциал в направлении обхода, в противном случае – со знаком минус.
|
|
|
Число независимых уравнений должно быть равно количеству токов, текущих в разных звеньях цепи.
Пример
Найдем силу тока и его направление, текущего через сопротивление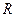 
в схеме на рис.5.12. Все сопротивления и ЭДС предполагаются известными.
Решение:
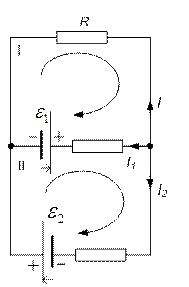
Рис. 5.12
Цепь содержит 
узла. Значит независимых уравнений типа (5.25) только одно:
.
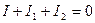Для верхнего замкнутого контура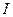 
:
.
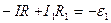Для нижнего замкнутого контура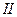 
:
.
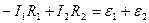Решая систему трех уравнений, получим:
.
Если после подстановки числовых значений окажется, что 
, то это значит, что ток течет так, как указано на рис.5.12, если же 
, то в противоположном направлении.
Дата добавления: 2021-03-18; просмотров: 46; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!