Потенциальная энергия взаимодействия точечных зарядов. Потенциал
Модуль 2.3
Теорема Гаусса в дифференциальной форме
Формула (1.17)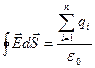 
является интегральной формой теоремы Гаусса. Найдем дифференциальную форму теоремы Гаусса, в которой устанавливается связь между объемной плотностью заряда 
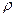и изменениями напряженности 
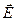в окрестности данной точки пространства.
Для этого представим сначала заряд 
в объеме 
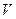, охватываемом замкнутой поверхностью 
, как 
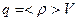, где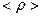 
- средняя по объему 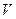значение объемной плотности заряда.
Затем подставим это выражение в уравнение (1.17) и разделим обе части его на 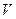. В результате получим:
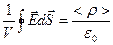(1.27)
Теперь устремим объем 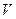к нулю, стягивая его к интересующей нас точке поля. Очевидно, что 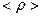будет стремиться к значению 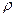в данной точке.
Предел отношения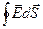 
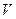к при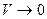 
называется дивергенцией поля 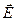и обозначается 
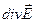. Таким образом, по определению:
(1.28)
Дивергенция происходит от латинского слова divergentia – расхождение. Аналогично (1.28) определяется дивергенция любого другого векторного поля в данной точке.
Отсюда
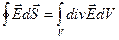(1.28а)
– теорема Остраградского - Гаусса или теорема о дивергенции. Она справедлива для любого векторного поля.
Чтобы получить выражение для дивергенции поля 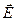, надо согласно (1.28) взять бесконечно малый объем 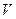, определить поток вектора 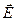сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Например, в декартовой системе координат выражение для дивергенции будет равно:
|
|
|
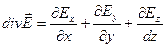. (1.29)
Итак, мы выяснили, что при 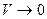в выражении (1.27) его правая часть стремится к 
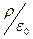, а левая – к .
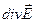Следовательно, мы приходим к формуле:
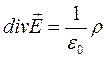, (1.30)
которая выражает теорему Гаусса в дифференциальной форме: дивергенция вектора 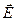в некоторой точке электростатического поля равна объемной плотности заряда в той же точке, деленной на 
.
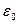Написание многих формул значительно упрощается, если ввести векторный дифференциальный оператор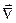 
(«набла»). В декартовых координатах он имеет вид:
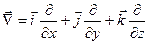, (1.31)
где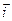 
, 
, 
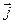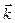– орты осей 
, 
, 
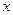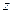. Если вектор 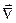умножить скалярно на вектор 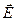, то получим:
,
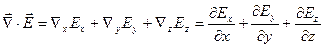а это есть не что иное, как 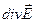, согласно (1.29). Таким образом, 
, и теорема Гаусса (1.30) будет иметь вид:
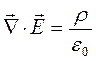(1.32)
|
|
|
В тех точках поля, где дивергенция 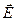положительна, мы имеем источники поля (положительные заряды), а тех точках, где она отрицательна – стоки (отрицательные заряды). Линии вектора 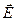выходят из источников поля, а в местах стоков они заканчиваются.
2.6. Работа сил электростатического поля. Циркуляция вектора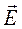 
Если задан вектор 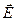, то можно говорить, что нам известно электростатическое поле.
На точечный заряд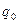 
, находящийся в электростатическом поле 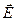, действует сила 
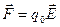. При перемещении заряда в поле эта сила совершает работу:
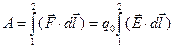. (1.33)
Докажем, что работа по перемещению заряда в электростатическом поле зависит лишь от его начального и конечного положений и не зависит от пути движения.
Доказательство: Пусть точечный заряд 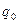находится в поле неподвижного точечного заряда и перемещается вдоль изображенной на рис. 1.24 траектории из положения 1 в положение 2. Найдем работу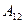 
, совершаемую при этом над зарядом 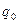силами поля. На заряд 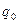действует кулоновская сила:
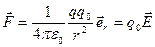, (1.34)
|
|
|
где 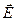– напряженность поля, создаваемого зарядом . Эта сила является центральной, т.к. ее модуль зависит только от расстояния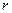 
до силового поля. Элементарная работа силы равна:
,
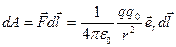где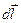 
– перемещение заряда .
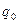Из рис. 1.24 следует, что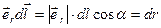 
. С учетом этого для работы 1-2 получается выражение:
. (1.35)
Полученный результат означает, что работа силы (1.34) не зависит от пути перемещения, а зависит лишь от начального и конечного положений заряда (от 
и 
).
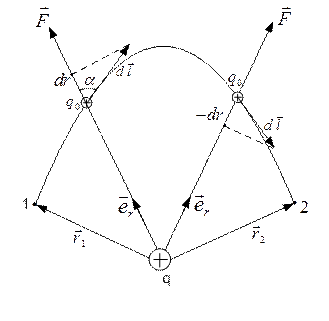
Рис. 1.24
Это результат можно было предвидеть, поскольку, как было показано в механике, центральные силы являются потенциальными. Работа потенциальных сил на любом замкнутом пути равна нулю: 
.Силовое поле, обладающее такими свойствами, называется потенциальным.
В случае электростатического поля:
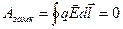, отсюда
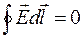. (1.36)
Интегрирование по замкнутому пути называется циркуляцией вектора 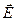и обозначается 
.
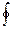Итак, циркуляция вектора 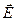по любому замкнутому контуру равна нулю – это есть теорема о циркуляции вектора 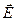, а также условие потенциальности электростатического поля.
Потенциальная энергия взаимодействия точечных зарядов. Потенциал
|
|
|
Работа потенциальных сил может быть представлена как убыль потенциальной энергии:
.
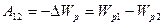Из формулы (1.35) следует, что:
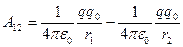
Приравняв эти два соотношения, будем иметь выражение для потенциальной энергии, которой обладает заряд 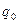в поле заряда :
.
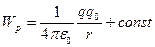Значение константы обычно выбирается так, чтобы при удалении заряда 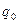от заряда на бесконечность (т.е. при 
) потенциальная энергия обращалась в нуль. При этом условии
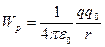. (1.37)
Скалярная величина
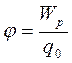. (1.38)
называется потенциаломполя в данной точке, он численно равен потенциальной энергии, которой обладал бы в данной точке единичный положительный заряд.
Из формулы (1.37) следует, что потенциал поля точечного заряда определяется выражением:
, (1.39)
где 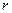– расстояние от заряда до данной точки поля.
Из определения потенциала (1.38) ясно, что любой заряд , находящийся в поле с потенциалом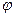 
, обладает потенциальной энергией:
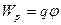. (1.40)
Следовательно, работу сил поля над зарядом можно выразить через разность потенциалов:
. (1.41)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению заряда на убыль потенциала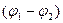 
, которая называется разностью потенциалов.
Таким образом, разность потенциалов равна:
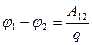. (1.42)
Если заряд из точки с потенциалом 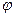удаляется на бесконечность, где 
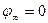, работа сил поля равна:
= 
.
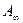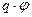Отсюда следует второе определение потенциала: потенциал
.
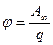численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из точки на бесконечность.
Дата добавления: 2021-03-18; просмотров: 78; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!