Интегрирование по частям в определенном интеграле

Понятие определенного интеграла

 

Пусть на отрезке [a , b] задана непрерывная функция f ( x ).

 

 

                                  y

                                M

                                  m

                                   0  a                 x_i                    b            x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a , b]

Разобьем отрезок [a , b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда x₁ – x₀ = Dx₁, x₂ – x₁ = Dx₂, … ,x_n – x_n-1 = Dx_n;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[x₀, x₁] ® m₁, M₁; [x₁, x₂] ® m₂, M₂; … [x_n-1, x_n] ® m_n, M_n.

Составим суммы:

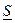_n = m₁Dx₁ + m₂Dx₂ + … +m_nDx_n =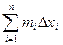

_n = M₁Dx₁ + M₂Dx₂ + … + M_nDx_n =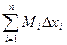

Сумма 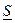 называется нижней интегральной суммой, а сумма  – верхней интегральной суммой.

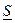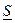Т.к. m_i £ M_i, то _n £ _n, а m(b – a) £ _n £ _n £ M(b – a)

Внутри каждого отрезка выберем некоторую точку e.

x₀ < e₁ < x₁, x₁ < e < x₂, … , x_n-1 < e < x_n.

 

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f ( x ) на отрезке [a , b].

S_n = f( e ₁ ) D x₁ + f( e ₂ ) D x₂ + … + f( e _n ) D x_n =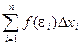

Тогда можно записать: m_i D x_i £ f ( e _i ) D x_i £ M_i D x_i

 

Следовательно, ,

 

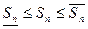
Геометрически это представляется следующим образом: график функции f ( x ) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

Обозначим max D x_i – наибольший отрезок разбиения, а min D x_i – наименьший. Если max D x_i ® 0, то число отрезков разбиения отрезка [a , b] стремится к бесконечности.

 

Если 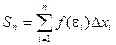 , то

 

Если при любых разбиениях отрезка [a , b] таких, что max D x_i ® 0 и произвольном выборе точек e_i интегральная сумма 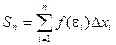 стремится к пределу S, который называется определенным интегралом от f ( x ) на отрезке [a , b].

 

       Обозначается: 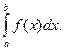, где

а – нижний предел интегрирования, b – верхний предел интегрирования, х – переменная интегрирования, [a , b] – отрезок интегрирования.

 

Пусть функция F ( x ) является первообразной для функции f ( x ) на некотором промежутке D, а числа a и b принадлежат этому промежутку.

Приращение F ( b ) – F ( a ) любых из первообразных функций F ( x ) + С при изменении аргумента от х=а до х= b называется определенным интегралом от функции f .

 

Вычисляется определенный интеграл по формуле Ньютона – Лейбница: 

 = F ( b ) – F ( a )

Свойства определенного интеграла

1) При перестановке пределов изменяется знак интеграла:

               = -

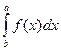
2) Интеграл с одинаковыми пределами равен нулю:

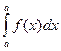                             = 0

3) Отрезок интегрирования можно разбить на части:

                             = +

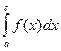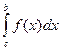
4) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов

5) Постоянный множитель можно вынести за знак определенного интеграла.

 

Пример. Вычислить определенный интеграл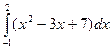  

Применяя формулу Ньютона-Лейбница и свойства определенного интеграла, получим:

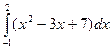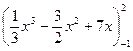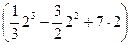= =  -  = 19,5

 

Замена переменной в определенном интеграле

Пусть задан интеграл , где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = j(t). Тогда если

1) j(a) = а, j(b) = b

2) j(t) и j¢(t) непрерывны на отрезке [a, b]

3) f(j(t)) определена на отрезке [a, b], то

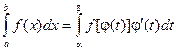
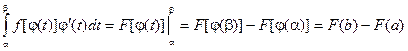
Интегрирование по частям в определенном интеграле

 

Если функции u = j(x) и v = y(x) непрерывны на отрезке [a , b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

           

---

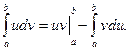
Дата добавления: 2021-03-18; просмотров: 68; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!