Потенциалы электромагнитного поля. Калибровка полей
Магнитное поле в среде
Уравнения Максвелла для стационарного магнитного поля в среде. Диамагнетики и парамагнетики
Уравнения Максвелла для магнитного поля (для электрического нет необходимости записывать)
Точечных источников магнитного поля нет. Все силовые линии замкнуты или уходят на бесконечность.
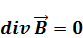
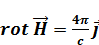 (для вакуума было
(для вакуума было 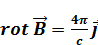 )
)
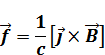
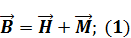
Возьмем ротор от (1):
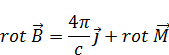

Под действием внешнего магнитного поля изменяется механический момент атома, следовательно изменяется магнитный момент. Если меняется механический момент, значит меняется магнитный момент. Как только пропадает внешнее магнитное поле все возвращается к первоначальному состоянию равномерного распределения. Как только вносим вещество во внешнее магнитное поле возникают молекулярные токи.
Диамагнетики
Диамагнетики – вещества, у которых в отсутствии магнитного поля отсутствует собственный магнитный момент.
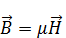
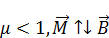
Парамагнетики
В электростатике собственного заряда нет. У атома могут быть собственные магнитные моменты.
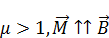
Ферромагнетики
Собственные магнитные моменты выстроены очень макроскопически. Все вещество можно разделить на некие домены. По сравнению с размерами атомов домены большие, по сравнению с веществом они маленькие. В каждом домене даже в отсутствии магнитного поля присутствует намагниченность. Переносим ферромагнетик во внешнее магнитное поле. У нас начинается перемагничиваться.
|
|
|
Если убрать внешнее магнитное поле, то начинается переориентация. Но при этом остается остаточная намагниченность вещества (петля гистерезиса). Минимальная потенциальная энергия соответствует нулевой намагниченности.
Интегральные соотношения и граничные условия в магнетиках

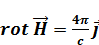 ; (2)
; (2)

Нормальная составляющая 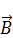 не терпит разрыва:
не терпит разрыва:
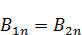
Тангенциальная составляющая 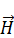 терпит разрыв:
терпит разрыв:
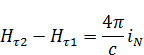
В векторной форму это будет записано как:
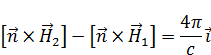
Интегральные соотношения. Получаем из интегрирования уравнений Максвелла:
Интегрируем поток вектора 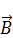 через замкнутую поверхность.
через замкнутую поверхность.
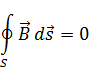

Циркуляция вектора 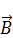 :
:
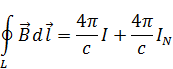
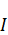 – свободные токи,
– свободные токи, 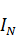 – молекулярные токи.
– молекулярные токи.
Квазистационарные электромагнитные поля
Уравнения Максвелла в среде
 – точечных источников магнитного поля нет
– точечных источников магнитного поля нет

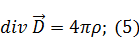
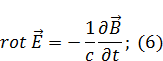
Найдем циркуляцию 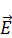 по какому-то контуру:
по какому-то контуру:
По теореме Стокса получается (поверхность не обязательно замкнутая и не обязательно плоская):
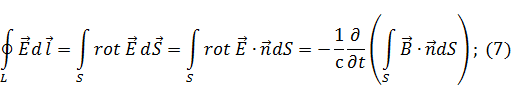
Это известный из электричества закон Фарадея, слева выражения (7) ЭДС:
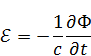
Что такое проинтегрированная напряженность? Это разность потенциалов. Разность потенциалов в начальной и конечной точке в принципе должны быть равны нулю, если поле потенциально. Но у на изменяемое магнитное поле, поэтому у нас поле перестает быть потенциальным, у нас возникает ЭДС. При прохождении заряда по полному контуру возникает разность потенциалов не равная нулю.
|
|
|
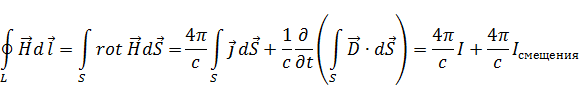
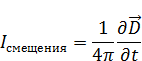
Потенциалы электромагнитного поля. Калибровка полей
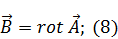
Подставляем (8) в (6):
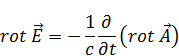
Перенесем все в одну сторону:


Получим запись вектора 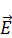 через оба потенциала:
через оба потенциала:
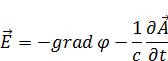
Уравнения Максвелла для вакуума (нет вещества):

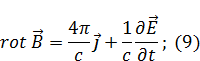
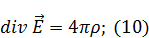
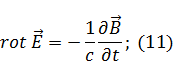
|
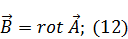
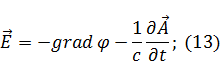
|
Подставим (13) в (10):
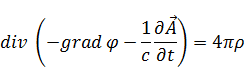
Дивергенция градиента — это лапласиан, в итоге:
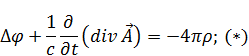
Нам мешает слагаемое  , чтобы получилось основное уравнение электростатики – уравнение Пуассона. Уравнения (12) и (13) не дают точное значение векторов
, чтобы получилось основное уравнение электростатики – уравнение Пуассона. Уравнения (12) и (13) не дают точное значение векторов 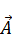 и
и  . Это дифференциальная запись, поэтому они заданы не точно. Мы можем задать новый вектор
. Это дифференциальная запись, поэтому они заданы не точно. Мы можем задать новый вектор 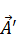 :
:
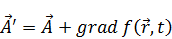
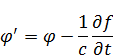
Изменение потенциалов не вносит изменения в вектора электрического и магнитного поля. Значит есть некая произвольность в выборе потенциалов. Если есть произвольность, то надо как-то откалибровать.
 – это кулоновская калибровка/нормировка.
– это кулоновская калибровка/нормировка.
Подставим (12), (13) в (9):
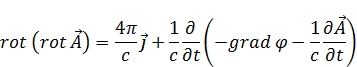
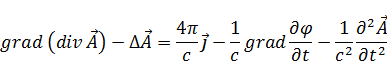
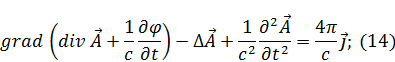
Можно ввести другую нормировку – нормировку Лоренца, она такая, что выражение в скобках равно нулю (14):
|
|
|

После введения нормировки выражение (14) примет вид:
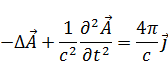
Это уравнение можно переписать через оператор Даламбера:

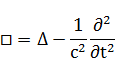
Подставим (15) в (*):

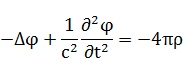
Через оператор Даламбера уравнение примет вид:
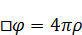
Теперь рассмотрим магнетики.
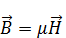

Уравнения Максвелла для вакуума (нет вещества):

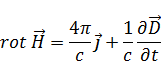
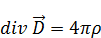
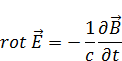
|
Тогда в магнетиках уравнения примут вид:

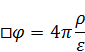
Дата добавления: 2021-03-18; просмотров: 76; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
