Статистическая мера информации

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Статистическая мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. В соответствии с этой мерой рассматривается не само событие, а информация о нём.

В 30-х годах XX века американский ученый Клод Шеннон предложил связать количество информации, которое несет в себе некоторое сообщение, с вероятностью получения этого сообщения. Вероятность p - количественная априорная (т.е. известная до проведения опыта) характеристика одного из исходов (событий) некоторого опыта. Измеряется в пределах от 0 до 1.

Если заранее известны все исходы опыта, сумма их вероятностей равна 1, а сами исходы составляют полную группу событий. Если все исходы могут свершиться с одинаковой долей вероятности, они называются равновероятными.

Количество информации, с точки зрения статистической меры информации невозможно определить без рассмотрения понятия неопределенности (энтропии) состояния системы. Это связано с тем, что в действительности получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы.

Если появляется сообщение о часто встречающемся событии, вероятность появления которого близка к единице, то такое сообщение для получателя малоинформативно. Столь же малоинформативны сообщения о событиях, вероятность появления которых близка к нулю.

События можно рассматривать как возможные исходы некоторого опыта, причем все исходы этого опыта составляю полную группу событий.

Пусть имеется N возможных исходов опыта, из них k разных типов, а i-й исход повторяется ni раз и вносит информацию, количество которой оценивается как Ii. Тогда средняя информация, доставляемая одним опытом:

Но количество информации в каждом исходе связано с его вероятностью pi и выражается в двоичных единицах (битах) как

(2)

где p_i – вероятность того, что система находится в i – м состоянии.

Полученную величину (2) называют энтропией и обозначают Н(а).

Если все события равновероятны и статистически независимы, т.е. их вероятности равны р_i= 1/N, оценка количества информации определяется соотношением:

Максимальное значение энтропии достигается при p = 0,5, когда два состояния равновероятны. При вероятностях р = 0 или р = 1, что соответствует полной невозможности или полной достоверности события, энтропия равна нулю.
Это свидетельствует о полном использовании информационной ёмкости системы. В случае неравных вероятностей количество информации, по Шеннону, меньше информационной ёмкости системы.

Пример. Пусть опыт состоит в сдаче студентом экзамена по информатике. Очевидно, у этого опыта всего 4 исхода (по количеству возможных оценок, которые студент может получить на экзамене). Тогда эти исходы составляют полную группу событий, т.е. сумма их вероятностей равна 1.

Если студент учился хорошо в течение семестра, значения вероятностей всех исходов могут быть такими: р(5) = 0.5; р(4) = 0.3; p(3) = 0,1; р(2) = 0.1, где запись p(j) означает вероятность исхода, когда получена оценка j (j = {2, 3, 4, 5}).

Если студент учился плохо, можно заранее оценить возможные исходы сдачи экзамена, т.е. задать вероятности исходов, например, следующим образом: p(5) = 0.1; p(4) = 0.2; р(3) = 0.4; р(2) = 0.3.

В обоих случаях выполняется условие:

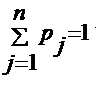где n - число исходов опыта, j - номер одного из исходов.

Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) – р_i. Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле: I = - log₂ p_i , где p_i - вероятность i-ro сообщения (исхода).

Пример. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для студента-хорошиста. Пусть I(j) - количество информации в сообщении о получении оценки j. В соответствии с формулой Шеннона имеем: I(5) = -log₂ 0,5 = 1, I(4) = -Iog₂ 0,3 = 1,74, I(3) = -log₂ 0,1 = 3,32, I(2) = -log₂ 0,1 = 3,32.

Пример. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для нерадивого студента: I(5) = -Iog₂0,1 = 3,32, I(4) = -log₂ 0,2 = 2,32, I(3) = -Iog₂ 0,4 = 1,32, I(2) = -Iog₂ 0,3 = 1,74.

Таким образом, количество получаемой с сообщением информации тем больше, чем неожиданнее данное сообщение. Этот тезис использован при эффективном кодировании кодами переменной длины (т.е. имеющими разную геометрическую меру): исходные символы, имеющие большую частоту (или вероятность), имеют код меньшей длины, т.е. несут меньше информации в геометрической мере, и наоборот.

Пример. После экзамена по Информатике, который сдавали ваши друзья, объявляются оценки («2», «3», «4» или «5»). Какое количество информации будет нести сообщение об оценке студента A, который выучил лишь половину билетов, и сообщение об оценке студента B, который выучил все билеты.

Опыт показывает, что для студента A все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке можно вычислить по формуле: I = log₂4 = 2 бит.

На основании опыта можно также предположить, что для студента B наиболее вероятной оценкой является «5» (p₁= 1/2), вероятность оценки «4» в два раза меньше (p₂= 1/4), а вероятности оценок «2» и «3» еще в два раза меньше (p₃= p₄ = 1/8). Так как события неравновероятны, воспользуемся для подсчета количества информации в сообщении формулой:

I = - (1/2·log₂1/2 + 1/4·log₂1/4 + 1/8·log₂1/8 + 1/8·log₂1/8) бит = 1,75 бит

Вычисления показали, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.

Пример. Определить среднее количество информации, получаемое студентом-хорошистом, по всем результатам сдачи экзамена. В соответствии с приведенной формулой (2) имеем:

I_ср = - (0,5*log₂0,5 + 0,3*log₂03 + 0,1*log₂0,l + 0,l*log₂0,l) = 1,67.

Пример. Определить среднее количество информации, получаемое нерадивым студентом, по всем результатам сдачи экзамена. В соответствии с приведенной формулой имеем:

I_ср = - (0,1* log₂0,l + 0,2*log₂0,2 + 0,4*log₂0,4 + 0,3*log₂0,3) = 1,73.

Большее количество информации, получаемое во втором случае, объясняется большей непредсказуемостью результатов: в самом деле, у хорошиста два исхода равновероятны.

Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. р₁ =р₂= 0,5. Тогда имеем в соответствии с формулой для расчета I_ср:

I_ср = - (0,5*log₂0,5 + 0,5* log₂0,5) = 1.

Эта формула есть аналитическое определение бита по Шеннону: это среднее количество информации, которое содержится в двух равновероятных исходах некоторого опыта, составляющих полную группу событий.

Единица измерения информации при статистическом подходе - бит. На практике часто вместо вероятностей используются частоты исходов. Это возможно, если опыты проводились ранее и существует определенная статистика их исходов. Так, строго говоря, в построении эффективных кодов участвуют не частоты символов, а их вероятности.

Дата добавления: 2021-03-18; просмотров: 104; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!