Среднеквадратичная ошибка оценки.

Линейная регрессия

Рассмотрим две непрерывные переменные

x=(x1, x2, .., xn), y=(y1, y2, ..., yn).

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

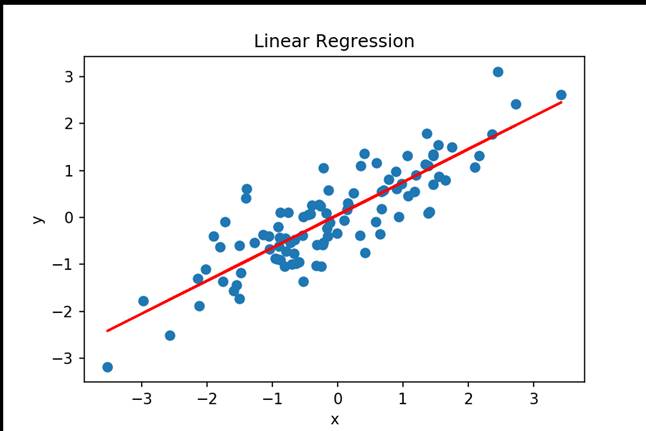
Рис.1.

Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса.

Различные виды зависимости переменных

Рис.2.

Простая линейная регрессия:

Y_i = β ₀ + β ₁ X_i + ε_i (1)

где β ₀ — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y),

β ₁ — наклон прямой Y,

ε_i— случайная ошибка переменной Y в i-м наблюдении.

Если верны некоторые предположения , в качестве оценки параметров генеральной совокупности (β ₀ и β ₁) можно использовать сдвиг a и наклон b прямой Y.

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии имеет вид:

Y=a+bx, (2)

где x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).

b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.

a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y.

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 3. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Метод наименьших квадратов

Выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Y_i = β ₀ + β ₁ X_i + ε_i

Рассмотрим при каких значениях коэффициентов a и b линейная функция

принимает наименьшее значение,

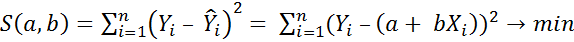
По необходимомму эктремума признаку частные производные должны быть приравнены к нулю.

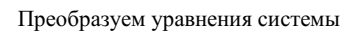
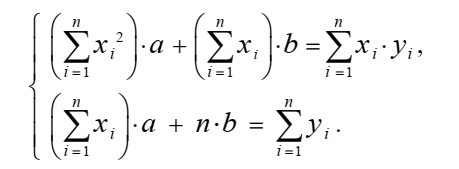
Определитель системы

не равен нулю. Система решается по формулам Крамера и имеет единственное решение.

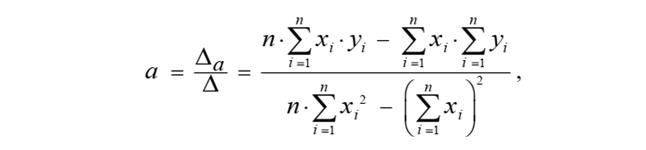
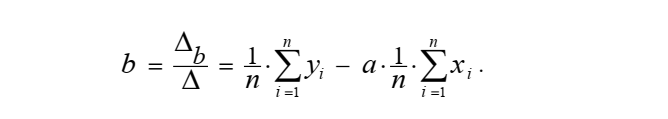
C уммы квадратов.

Предсказать значение зависимой переменной Y по значениям независимой переменной x в рамках избранной статистической модели:

1. Полная (общая) сумма квадратов (total sum of squares — SST)

SST=SSR+SSE.

Позволяет оценить колебания значений Y_i вокруг среднего значения Y ̅.

Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением

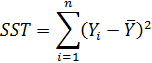
2. Сумма квадратов регрессии (regression sum of squares — SSR).

Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷi (предсказанным значением переменной Y) и Y̅ (средним значением переменной Y).

Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:

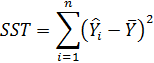
3 Сумма квадратов ошибок (error sum of squares — SSE).

Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.

Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:

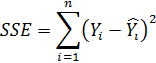
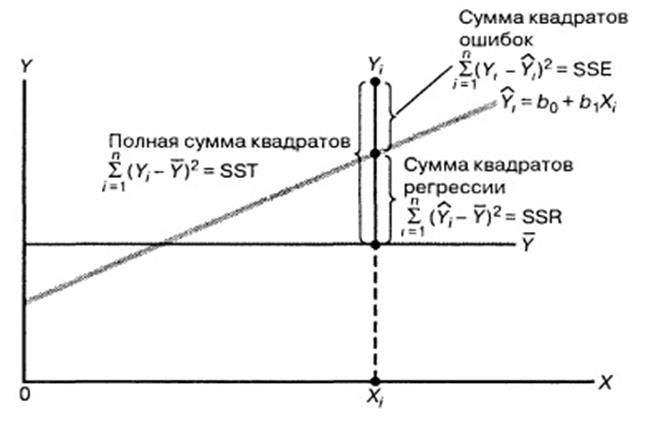
Рис.5.

Среднеквадратичная ошибка оценки.

Оценка отклонения предсказанных значений переменной Y от ее реальных значений.

Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Показано на рис. 5.

Среднеквадратичная ошибка оценки

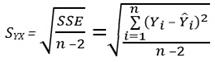
где Y_i — фактическое значение переменной Y при заданном значении X _i,

Ŷ _i — предсказанное значение переменной Y при заданном значении X _i,

SSE — сумма квадратов ошибок.

Дата добавления: 2021-03-18; просмотров: 60; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!