Определение проверочных равенств
Пользуясь таблицей опознавателей одиночных ошибок в каждом из разрядов, нетрудно определить, символы каких разрядов должны входить в каждую из проверок на четность.
Возьмем в качестве примера табл. 2.1 опознавателей для кодов, предназначенных исправлять одиночные ошибки. В принципе можно построить код, усекая эту таблицу на любом уровне. Однако оптимальными будут коды, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов, например код (7,4) n=7, к=4.
То есть при трех проверочных разрядах опознавателя мы можем передавать четыре информационных символ. Найдем места и значения проверочных разрядов.
Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1-го, 3-го, 5-го и 7-го разрядов :
.
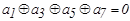Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда, второе проверочное равенство должно иметь вид :
.
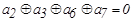Аналогично находим и третье равенство :
.
Чтобы эти равенства при отсутствии ошибок удовлетворялись при любых значениях информационных символов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них входил только в одно из равенств. Это обеспечит однозначное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлетворяют разряды, по одному разу входящие в полученные уравнения. В нашем случае это будут первый, второй и четвертый разряды.
|
|
|
Таким образом, для кода (7,4), исправляющего одиночные ошибки, искомые правила построения кода, т.е. соотношения, реализуемые в процессе кодирования, принимают вид :
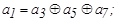
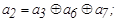
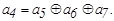
Введение проверочного разряда, обеспечивающего четность числа единиц во всей кодовой комбинации,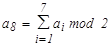 
позволяет построить код (8,4), способный одновременно исправлять одиночные ошибки и обнаруживать двойные.
Используя таблицу опознавателей (табл.2.3) и рассуждая аналогичным образом, можно составить проверочные равенства для любого кода, исправляющего одиночные и двойные независимые ошибки. Например, для кода (8,2). Минимальное число разрядов в кодовой комбинации должно быть менее 
. Находятся из уравнения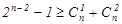 
. При n = 7 имеем 
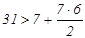. Однако, из табл. 2.3 для опознавателя кодовой комбинации из 7 разрядов требуется 6 разрядов. Поэтому приходится применить код (8,2). Соотношения, которые необходимо реализовать в процессе кодирования и декодирования этого кода:
|
|
|
| 1. |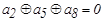 
| 
|
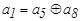
| 2. | 
|
|
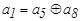
| 3. | 
| 
|
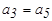
| 4. |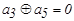 
| 
|
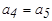
| 5. |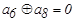 
| 
|
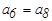
| 6. |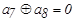 
| 
|
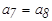
Эти уравнения, как и уравнение для кода (7,4), получаются из вертикальных столбцов опознавателей.
ЗАДАНИЕ
1. Ознакомится с принципами построения групповых кодов.
2. Закодировать алфавит сообщения, использованного в лабораторных работах 1 и 2 линейным групповым кодом при допущении, что ошибка будет одиночной.
3. Доказать правильность кодировки с помощью проверочных уравнений.
Дата добавления: 2021-03-18; просмотров: 153; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!