Применение свойств непрерывности.
Непрерывность функции.
Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, и если, для любого сколь угодно малого положительного числа ε > 0, существует такое число δε > 0, зависящее от ε, что для всех x, принадлежащих δε - окрестности точки x0: │ x - x0│< ε, значения функции принадлежат ε - окрестности точки f(x0): │f ( x) – f (x0)│< ε.
Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную ∆x=x – x 0 , которая называется приращением переменной x в точке x 0. Далее мы рассматриваем новую функцию: ∆f= f ( x) – f (x0)= f (x0+∆x ) - f (x0).
Ее называют приращением функции в точке x 0. Считаем, что она зависит от ∆x переменной : ∆f= f (x0+∆x ) - f (x0). Тогда можно дать еще одно определение.
Определение непрерывности функции в точке в терминах приращений
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности этой точки, и если предел приращения этой функции в точке ∆f, при ∆x стремящемся к нулю, равен нулю.
Свойства непрерывности в точке.
|
|
|
1. Если функции f (x); g(x) непрерывны в точке x = a, то в этой точке непрерывными будут также функции: f (x)±g(x); f (x)·g(x);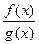 
, если g (а)≠0.
2. Если функция t (x) непрерывна в точке x=a, а функция f ( t) непрерывна в соответствующей точке t 0=f ( a ), то и сложная функция f ( t ( x )) непрерывна в точке x=a.
3. Все элементарные функции непрерывны в каждой точке их областей определения.
4. (Ограниченность непрерывной функции). Если функция y = f ( x ) непрерывна в точке x = a, то существует окрестность этой точки, в которой заданная функция ограничена.
5. (Про устойчивость знака непрерывной функции). Если функция y = f ( x ) непрерывна в точке x = a ; f ( a )≠0, то существует окрестность этой точки, в которой f ( x )≠0, причем знак функциb в этой окрестности совпадает со знаком f ( a ).
Непрерывность функции на промежутке
ОПРЕДЕЛЕНИЕ
Функция y = f ( x ) называется непрерывной на интервале ( a ; b ), если она непрерывна в каждой точке этого интервала.
Функция y = f ( x ) называется непрерывной на отрезке [a ; b], если она непрерывна на интервале ( a ; b ), непрерывна справа в точке a и непрерывна слева в точке b.
Замечание. Функция, непрерывная на отрезке [a ; b] может быть разрывной в точках a и b.
Свойства непрерывности на промежутке.
|
|
|
1. (Об ограниченности непрерывной на отрезке функции). Если функция y = f ( x ) непрерывна на отрезке [a ; b], то она и ограничена на этом отрезке, то есть существует такое число M>0, что для любого x 
[a ; b] выполняется неравенство │f ( x )│≤ M.
2. (Теорема Вейерштрасса). Если функция y = f ( x ) непрерывна на отрезке [a ; b], то она достигает на этом отрезке своего наибольшего M и наименьшего m значений.
3. (О существовании нуля на отрезке непрерывности). Если функция y = f ( x ) непрерывна на отрезке [a ; b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале ( a ; b ) найдется по крайней мере одна точка 
c, в которой f ( c )=0.
4. (Теорема Больцано-Коши). Если функция y = f ( x ) непрерывна на отрезке [a ; b], то она принимает на интервале ( a ; b ) все промежуточные значения между f ( a ) и f ( b ).
5. (О существовании непрерывной обратной функции). Пусть функция y = f ( x ) определена, строго монотонна и непрерывна на отрезке [a ; b]. Тогда на отрезке [α ;β], где α=f ( a ), β= f ( b ) , существует обратная функция x = f-1( y ) также строго монотонная и непрерывная на отрезке [α ;β].
Применение свойств непрерывности.
Пример 1. Доказать, что уравнение х4 – 3х2+2х – 1=0 имеет по меньшей мере один вещественный корень в интервале [1; 2].
|
|
|
Решение.
Пусть f ( x )= х4 – 3х2+2х – 1 .
Вычислим значения функции при x = 1 и x = 2.
.
.
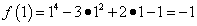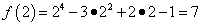Получили, что функция на концах интервала принимает значения разных знаков:
f(-1)<0 и f(7)>0, т. е.
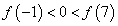
Следовательно, в интервале [1; 2] существует такое число a, при котором f(a) = 0. То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.
Пример 2. Есть ли у уравнения sin x – x+1=0 хотя бы один вещественный корень?
Решение.
Функция f ( x )= sin x – x+1 определена на интервале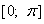 
.
Вычислим значения функции при x = 0 и 
.
.
.
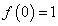Получил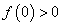и
и 
.
Следовательно, существует такое число a, при котором f(a) = 0.
Ответ на вопрос задачи: уравнение имеет по меньшей мере один вещественный корень.
Дата добавления: 2021-03-18; просмотров: 194; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!