Функциональные и степенные ряды.
Разложение функций в степенные ряды
Ряд вида 
, слагаемые которого 
, 
,..., 
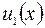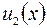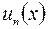,… являются функциями переменной 
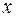, называется функциональным рядом. Давая переменной 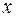определенные числовые значения, мы получим разные числовые ряды, некоторые из них могут оказаться сходящимися, другие - расходящимися. Целью исследования рядов из функций является нахождение значений 
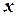, для которых числовой ряд является сходящимся. Совокупность всехзначений 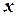, при которых функциональный ряд сходится, называют областью сходимости функционального ряда.
Областью сходимости функционального ряда чаще всего служит какой-нибудь промежуток оси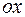 
. Каждому значению 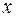из области сходимости функционального ряда соответствует определенное значение предела 
, являющееся функцией от 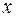. Его называют суммой функционального ряда и обозначают 
.
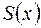Ряд вида
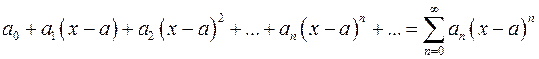, (5.1)
составленный из степенных функций (коэффициенты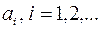 
- действительные числа), называется степенным рядом. Именно такой вид функциональных рядов мы и будем рассматривать. Если 
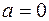, степенной ряд приобретает вид
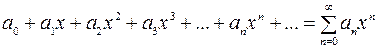. (5.2)
Заметим, что в точке 
степенной ряд (5.2) всегда сходится.
Для нахождения области сходимости степенного ряда используется теорема Абеля. Если степенной ряд (5.2) сходится при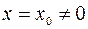 
, то он сходится, и притом абсолютно, для всех значений 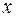, удовлетворяющих неравенству 
. Если же степенной ряд (5.2) расходится при 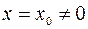, то он расходится и для всех значений 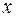таких, что 
.
|
|
|
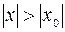Из теоремы Абеля вытекает, что всякая точка сходимости степенного ряда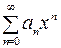 
расположена не дальше от точки 
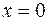, чем всякая точка его расходимости. Поэтому существует интервал 
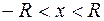, для всех точек которого степенной ряд (5.2) сходится, а для всех : 
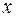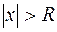– расходится.
Интервал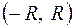 
называется интервалом сходимости степенного ряда (5.2), а число 
- радиусом сходимости степенного ряда. На концах интервала сходимости (т.е. пр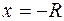и 
и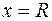 
) ряд может как сходиться, так и расходиться. Поэтому концевые точки интервала сходимости 
исследуются отдельно.
Радиус сходимости степенного ряда можно вычислять по одной из формул 
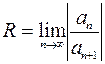или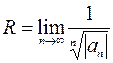 
при условии, что входящие в них пределы существуют.
Интервал сходимости рядов вида (5.1) симметричен относительно точки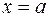 
и описывается неравенствами 
.
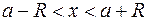Найдем, например, область сходимости степенного ряда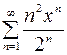 
. Выпишем коэффициенты 
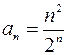и 
. Тогда
= 
= 
.
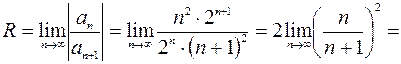
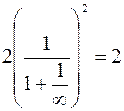Следовательно, ряд сходится, если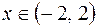 
. Осталось исследовать ряд в концевых точках 
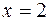и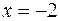 
.
При 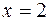степенной ряд принимает вид 
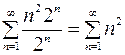. Это числовой знакоположительный ряд. Он расходится, т.к. не выполняется необходимое условие сходимости 
.
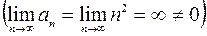При 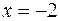степенной ряд принимает вид 
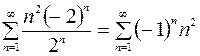. Это числовой знакочередующийся ряд. Так как 
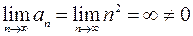, то ряд расходится. Таким образом, область сходимости ряда 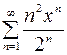совпадает с его интервалом сходимости: .
|
|
|
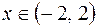Для степенного ряда 
выпишем коэффициент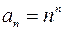 
. Радиус сходимости найдем по другой формуле: 
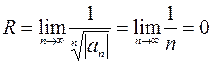. Получили, что ряд сходится только в одной точке . Она и является его областью сходимости.
Исследуем далее степенной ряд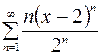 
, который относится к виду (5.1). Выпишем коэффициенты 
и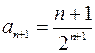 
, найдем радиус сходимости
.
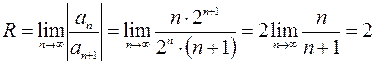Здесь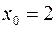 
, следовательно, ряд сходится при 
, т.е. при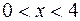 
. Осталось исследовать ряд в концевых точках и 
.
При степенной ряд принимает вид
.
Это числовой знакоположительный ряд, который расходится, т.к.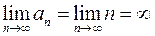 
(необходимое условие сходимости не выполняется).
При степенной ряд принимает вид
.
Это числовой знакочередующийся ряд, который расходится по той же причине ( 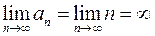). Тем самым, область сходимости заданного степенного ряда: 
.
Мы рассмотрели задачу нахождения области сходимости степенных рядов. При этом сумма всякого степенного ряда является некоторой функцией, определенной внутри его области сходимости. В связи с этим возникает обратная задача: для некоторой функции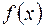 
найти степенной ряд, сумма которого в области сходимости равна исходной функции 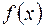. Такой ряд называется разложением функции в степенной ряд.
|
|
|
Для решения поставленной задачи потребуется формула Тейлора. Пусть функция 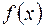имеет в некотором замкнутом отрезке 
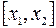непрерывные производные до 
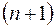-го порядка включительно, а точка 
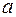находится внутри этого отрезка. Тогда для любого 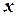из интервала 
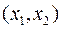справедлива формула Тейлора
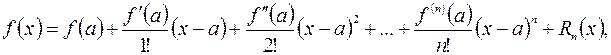где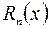 
– остаточный член, который может быть записан в виде
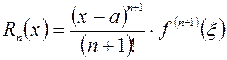(форма Лагранжа), причем число 
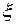лежит между 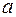и 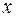(его можно представить в виде 
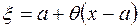), где 
.
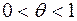Если в формуле Тейлора взять 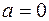, то получим частный случай этой формулы – формулу Маклорена
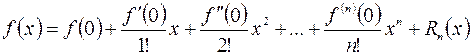
Формулы Тейлора и Маклорена показывают, что функцию 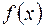можно оценить многочленом 
-ой степени. Ошибка вычисления будет равна .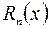
Пусть функция 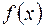имеет в интервале 
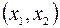, содержащем точку 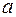, производные любого порядка и, кроме того, для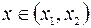 
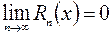. Тогда функция 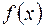может быть представлена рядом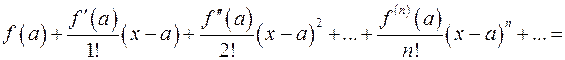 
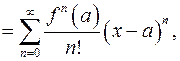(5.3)
который сходится, и его суммой будет функция 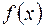. Представление функции 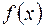в виде такого ряда называется разложением этой функции в ряд Тейлора.
При 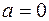получим частный случай ряда Тейлора
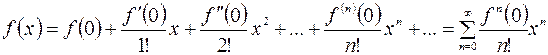, (5.4)
который называют рядом Маклорена.
|
|
|
Видим, что вопрос о разложении функции в ряд сводится к исследованию поведения остаточного члена 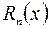при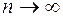 
. В частности, остаточный член 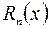стремится к нулю, когда производные функции 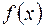ограничены в совокупности в интервале 
, т.е. когда при каждом натуральном и каждом 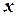из этого интервала выполняется неравенство 
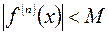, где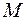 
- положительная постоянная.
Итак, для разложения функции 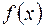в степенной ряд нужно сначала формально составить для нее ряд Тейлора. С этой целью вычисляют производные функции в точке 
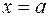и подставляют их в разложение (5.3). Затем необходимо найти область сходимости полученного ряда и выяснить, для каких значений 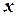из этой области сходимости можно поставить знак равенства между функцией 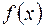и ее рядом Тейлора.
Разложим, например, функцию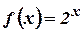 
в ряд Маклорена (по степеням 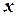). Найдем числовые значения производных функции 
в точке :
, 
, 
, 
.
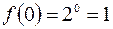
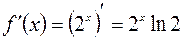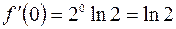
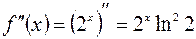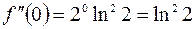
Отсюда легко установить закономерность образования производной -го порядка: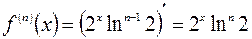 
, 
.
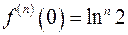Подставляя теперь значения этих производных в ряд (5.4), получаем ряд Маклорена для функции :
= 
.
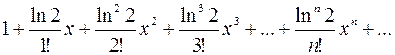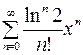Находим область сходимости полученного ряда. Так как
= 
,
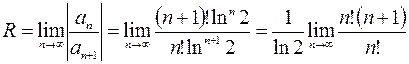то ряд сходится для всех значений .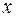
Выясним, для каких значений 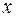найденное разложение сходится к функции 
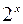. С этой целью заметим, что ввиду справедливости неравенства 
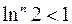производные всех порядков функции на любом отрезке 
, ограничены одним и тем же числом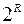 
: 
. Отсюда следует, что найденное разложение сходится к функции 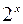при всех значениях 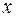, т.е. 
.
Во многих случаях можно пользоваться готовыми рядами, составленными для элементарных функций. Основными табличными разложениями назовем следующие разложения:
, 
;
, ;
;
=
= 
, 
( 
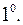
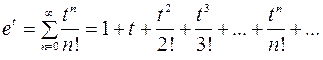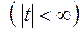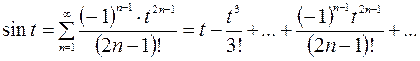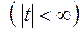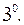
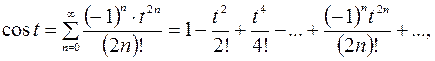
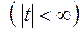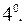
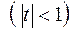
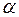– любое действительное число). Ряд называется биномиальным.
Eсли положить 
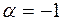и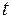 
заменить на 
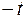, то получим ряд, который является геометрической прогрессией
, ;
, ( 
);
, ( 
).
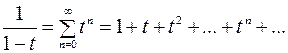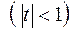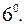
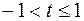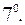
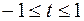Например, чтобыразложить функцию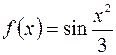 
в ряд Маклорена, используем табличное разложение синуса, полагая 
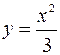. Тогда 
=
= 
.
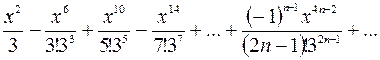Так как разложение функции 
в ряд имеет место для всех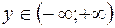 
, то и разложение функции 
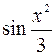имеет место для всех 
.
Степенные ряды можно использовать для приближенных вычислений значений функции в точке. Для этого исходную функцию 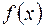раскладывают в степенной ряд, сохраняя первые членов разложения, отбрасывая остальные. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов.
Если данный ряд знакопостоянный, то ряд, состоящий из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. В случае знакочередующегося ряда, члены которого удовлетворяют признаку Лейбница, используется оценка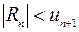 
, где 
– первый из отброшенных членов ряда.
Вычислим, например,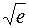 
с точностью 
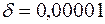.Для этого используем готовое разложение функции 
в степенной ряд по степеням :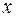 
.
Полагая в данном равенстве 
, получим
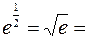
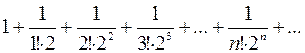
Определим, сколько членов ряда следует взять, чтобы погрешность приближенного равенства
не превышала заданного числа .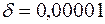
Погрешность этого приближенного равенства 
определяется суммой членов ряда, следующих после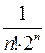 
в разложении :
,
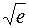или
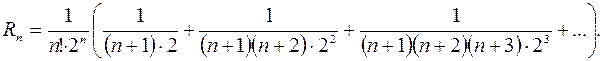
Заменив каждый из сомножителей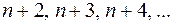 
меньшей величиной 
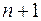, получим неравенство:
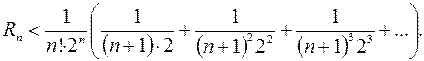
В скобке получаем бесконечно убывающую геометрическую прогрессию с первым членом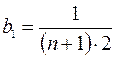 
и знаменателем прогрессии 
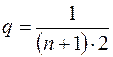. Запишем ее сумму по формуле
.
Тогда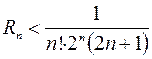 
.
Далее подбором определяем, при каком натуральном значении будет выполняться неравенство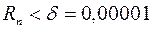 
. Полагая, к примеру, 
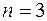имеем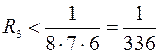 
. (нельзя сказать с уверенностью, что 
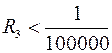). Пусть далее 
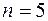. Тогда 
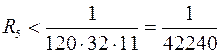. Пусть, наконец, 
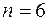. Тогда 
, т.е.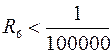 
и можно принять 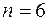. Следовательно,
=
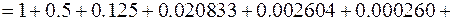
Значит 
с точностью .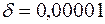
Заметим, что каждое слагаемое мы вычисляли с точностью до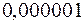 
, чтобы при суммировании не получить погрешности, превышающей 
.
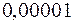Вычислим далее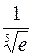 
с точностью 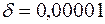.Используем готовое разложение функции в степенной ряд по степеням 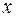, взяв 
:
.
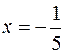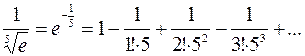Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница, а потому допускаемая погрешность по абсолютной величине будет меньше первого из отброшенных членов ряда. Нетрудно видеть, что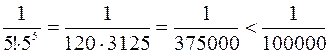 
. Поэтому можно отбросить это слагаемое и воспользоваться приближенным равенством
.
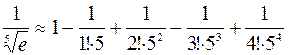Тем самым, 
.
Степенные ряды применяют также для вычисления определенных интегралов . Если требуется вычислить определенный интеграла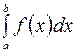 
с заданной точностью 
, топодынтегральную функцию 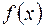нужно разложить в ряд Маклорена, пользуясь готовыми разложениями функций 
, 
, 
, 
, 
, 
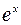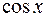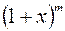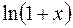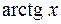. Далее в области сходимости полученный ряд интегрируют почленно (для каждого слагаемого находят определенный иетеграл) если ряд явялется рядом Лейбница, отбрасывают все слагаемые, начиная с того, который по модулю меньше числа . Суммируя оставшиеся слагаемые, записываем ответ.
Вычислим, например, 
с точностью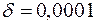 
. Раскладываем подынтегральную функцию 
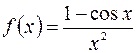в ряд Маклорена, используя готовое разложение функции 
:
.
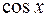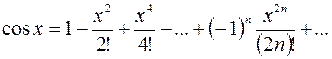Получим
=
= 
.
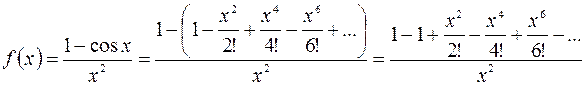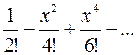Область сходимости полученного ряда – вся числовая ось. Далее находим первообразные функции для каждого из слагаемых этого степенного ряда
=
= 
.
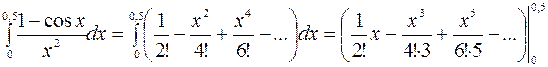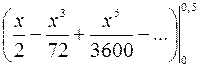Используя формулу Ньютона-Лейбница, получаем
.
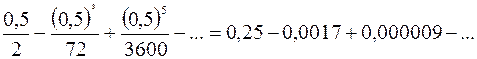Все члены полученного числового ряда, начиная с третьего, отбрасываем, поскольку третий член ряда равен 
и он меньше заданной точности 
. Окончательно получаем
.
Контрольные задания
Задание 1
Решить дифференциальное уравнение с разделяющимися переменными
1.01.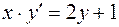 
.
1.02.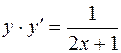 
.
1.03. 
.
1.04.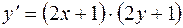 
.
1.05.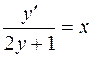 
.
1.06.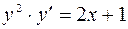 
.
1.07.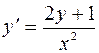 
.
1.08. 
.
1.09.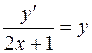 
.
1.10.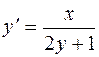 
.
Контрольное задание 2
Решить задачу Коши
| 2.01. |  ,  .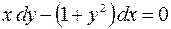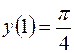
|
| 2.02. |  ,  .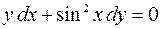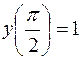
|
| 2.03. |  ,  .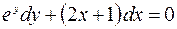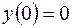
|
| 2.04. |  ,  .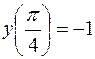
|
| 2.05. |  ,  .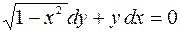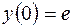
|
| 2.06. |  ,  .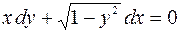
|
| 2.07. |  , .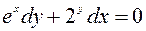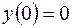
|
| 2.08. |  , .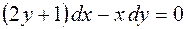
|
| 2.09. |  ,  .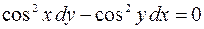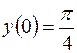
|
| 2.10. |  , .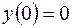
|
Контрольное задание 3
Найти общее решение уравнений
3.01.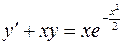 
.
3.02.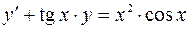 
.
3.03. 
.
3.04. 
.
3.05.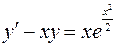 
.
3.06.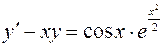 
.
3.07. 
.
3.08.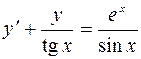 
.
3.09.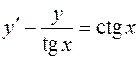 
.
3.10.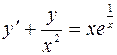 
.
Контрольное задание 4
Решить задачу Коши
4.01.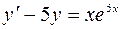 
, 
.
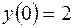4.02.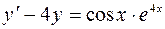 
, 
.
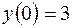4.03.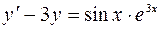 
, 
.
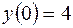4.04.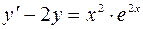 
, 
.
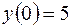4.05. 
, 
.
4.06.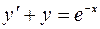 
, 
.
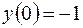4.07. 
, 
.
4.08.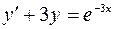 
, 
.
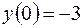4.09.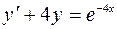 
, 
.
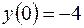4.10.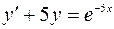 
, 
.
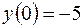Контрольное задание 5
Решить задачу Коши
5.01. 
, 
.
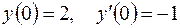5.02. 
, 
.
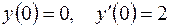5.03.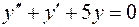 
, 
.
5.04.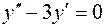 
, 
.
5.05.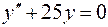 
, 
.
5.06.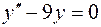 
, 
.
5.07. 
, 
.
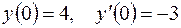5.08.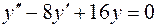 
, 
.
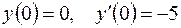5.09.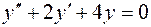 
, 
.
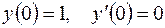5.10.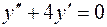 
, 
.
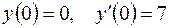Контрольное задание 6
Найти общее решение неоднородных дифференциальных уравнений
6.01. 
.
6.02. 
.
6.03.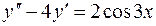 
.
6.04.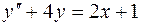 
.
6.05.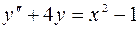 
.
6.06.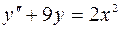 
.
6.07.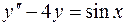 
.
6.08.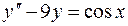 
.
6.09.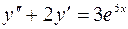 
.
6.10.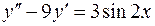 
.
Контрольное задание 7
Найти решение неоднородного дифференциального уравнения, удовлетворяющее начальным условиям
7.01.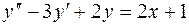 
; .
7.02. 
; 
.
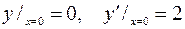7.03.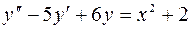 
; 
.
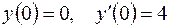7.04.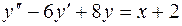 
; 
.
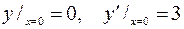7.05.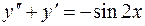 
; 
.
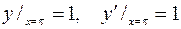7.06. 
; 
.
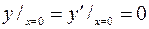7.07.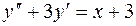 
; 
.
7.08.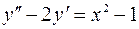 
; 
.
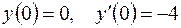7.09.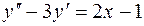 
; 
.
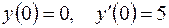7.10.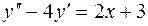 
; .
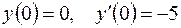Контрольное задание 8
Вычислить сумму ряда
8.01. 
.
8.02.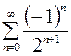 
.
8.03. 
.
8.04.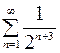 
.
8.05.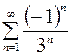 
.
8.06.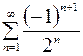 
.
8.07. 
.
8.08. 
.
8.09.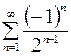 
.
8.10.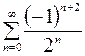 
.
Контрольное задание 9
Исследовать числовой знакопостоянный ряд на сходимость
9.01.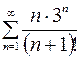 
.
9.02. 
.
9.03.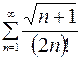 
.
9.04.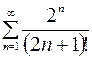 
.
9.05.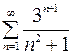 
.
9.06. 
.
9.07. 
.
9.08.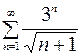 
.
9.09.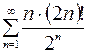 
.
9.10.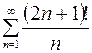 
.
Контрольное задание 10
Исследовать числовой знакочередующийся ряд на сходимость
10.01.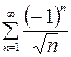 
.
10.02.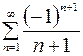 
.
10.03. 
.
10.04.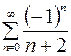 
.
10.05.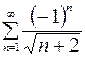 
.
10.06.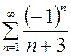 
.
10.07.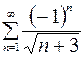 
.
10.08.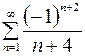 
.
10.09. 
.
10.10.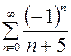 
.
Контрольное задание 11
Найти область сходимости степенного ряда
| 11.01. |  .
| 11.06. |  .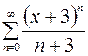
| |
| 11.02. |  .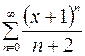
| 11.07. |  .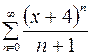
| |
| 11.03. |  .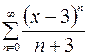
| 11.08. |  .
| |
| 11.04. |  .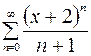
| 11.09. |  .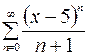
| |
| 11.05. |  .
| 11.10. |  .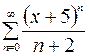
|
Контрольное задание 12
Разложить функцию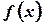 
в ряд Маклорена (по степеням )
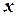| 12.01. |  .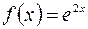
|
| 12.02. |  .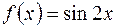
|
| 12.03. |  .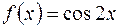
|
| 12.04. |  .
|
| 12.05. |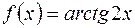 
|
| 12.06. |  .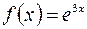
|
| 12.07. |  .
|
| 12.08. |  .
|
| 12.09. |  .
|
| 12.10. |  .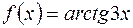
|
ЛИТЕРАТУРА
1. Пискунов, Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие для втузов. Т.2 / Н.С.Пискунов.- М.: Интеграл - Пресс, 2001.-544 с.
2. Шипачев, В.С. Высшая математика: Учеб. для студентов вузов/ В.С.Шипачев. 4-е изд., - М.: Высш. шк., 2000.-480 с.
3. Минорский,В.П. Сборник задач по высшей математике: учеб. пособие для втузов /В.П.Минорский. -М.: Изд-во физ.-мат. лит., 2004.-336с
4. Сборник задач по математике для втузов/ под ред. А.В.Ефимова, Б.П.Демидовича. - М.: Наука, 1981. – 304 с.
5. Важдаев В.П., Коган М.М., Лиогонький М.И., Протасова Л.А. 64 лекции по математике. Книга 2.- Н.Новгород: ННГАСУ, 2012. – 200 с.
СОДЕРЖАНИЕ
§ 1. Дифференциальные уравнения первого порядка………….....3
§ 2. Линейные однородные дифференциальные уравнения
второго порядка……………………………………………………..11
§ 3. Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами…………..…..18
§ 4. Числовые ряды………………………………………………....23
§ 5. Функциональные и степенные ряды. Разложение функций
в степенные ряды……………………………………………….….38
Контрольные задания……………………………………………....50
Литература……………………………………………………….….60
| Павел Валерьевич Столбов Людмила Анатольевна Протасова |
Дата добавления: 2021-03-18; просмотров: 111; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!