Нормальная составляющая ускорения

Скалярная и вектроная скорость

Сре́дняя ско́рость — в кинематике, некоторая усреднённая характеристика скорости движущегося тела (или материальной точки). Различают два основных определения средней скорости, соответствующие рассмотрению скорости как скалярной либо векторной величины: средняя путевая скорость (скалярная величина) и средняя скорость по перемещению (векторная величина). При отсутствии дополнительных уточнений, под средней скоростью обычно понимают среднюю путевую скорость.

Скаляр (от лат. scalaris — ступенчатый) — величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается вещественное число).

При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонентов вектора, которые могут быть разными у одного и того же вектора в разных системах координат.

· В общей и линейной алгебре — элемент основного поля (например, поля вещественных или комплексных чисел).

· В тензорном исчислении — тензор валентности (0,0), при замене базиса системы координат не меняется.

· В современной физике, подразумевающей пространственно-временной подход, под скаляром обычно имеется в виду пространственно-временной скаляр, лоренц-инвариантнаявеличина, не меняющаяся при переходе от одной инерциальной системы отсчёта к другой (а в общей теории относительности и других метрических теориях гравитации — скаляр остается неизменным также и при переходе к неинерциальным системам отсчёта). В этом отличие от ньютоновской физики, где под скаляром понимается обычный скаляр обычного трёхмерного пространства (так, энергия в ньютоновском смысле — скаляр, а в пространственно-временном — лишь компонента четырёхмерного вектора).

Вектором скорости называют вектор, определяющий быстроту и направление движения.
Вектором средней скорости называют отношение вектора перемещения к промежутку времени, за который это перемещение происходит.
Так как в произвольном случае движения вектор перемещения за конечный промежуток времени не определяет точно направление движения, это не может сделать и вектор средней скорости. Следовательно, необходимо рассматривать перемещения за бесконечно малые промежутки времени.
Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:
Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость движения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости).

Компоненты средней скорости равны.
Вектор скорости с его компонентами связан такими же по виду соотношениями, как радиус-вектор с координатами точек.

Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора.
скорости. Аналогично определениям для вектора скорости вводятся понятия среднего и мгновенного ускорения.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 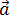_n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

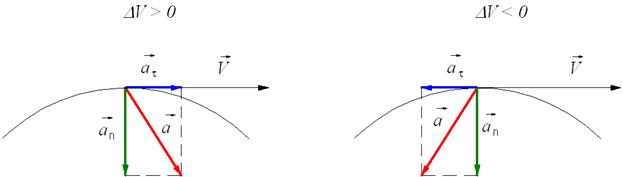
Нормальное ускорение равно квадрату угловой скорости помноженному на радиус траектории

Для достаточно малого промежутка времени Δt справедливы следующие соотношения:

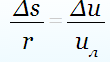
Так как:

Δs= u_л Δt

Имеем

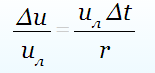
Отсюда получается радиальное ускорение

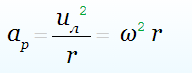
Тот же результат можно получить рассмотрев координаты лежащей на окружности точки Р, в которой в данный момент находится тело

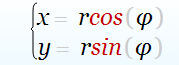
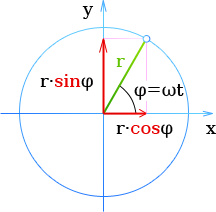
Из выражения Равномерное движение тела по окружности следует

φ= ωt

Согласно формуле Мгновенное ускорение, ускорение представляет собой вторую производную перемещения по времени. Продифференцировав дважды координаты точки Р, найдем ускорения в направлении осей координат:

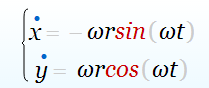
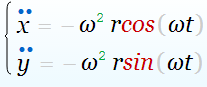
Отсюда для результирующего ускорения имеем

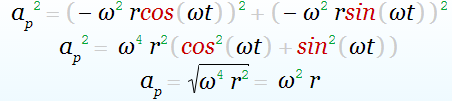
Потенциал ускорения

скалярная функция Ф пространственных координат и времени t, градиент которой равен вектору ускорения W.
Существует для безвихревых течений и при движении несжимаемой жидкости удовлетворяет, как и потенциал скорости, уравнению Лапласа. В аэро- и гидродинамике используется при исследовании обтекания профилей и крыльев дозвуковыми и сверхзвуковыми потоками идеального газа на основе линеаризованных уравнений.

Скорость в различных неравномерных движениях изменяется по разному. Например, товарный поезд, отходя от станции, движется ускоренно; на перегоне — то ускоренно, то равномерно, то замедленно; подходя к станции, он движется замедленно. Пассажирский поезд также движется неравномерно, но его скорость изменяется быстрее, чем у товарного поезда. Скорость пули в канале ствола винтовки возрастает от нуля до сотен метров в секунду за несколько тысячных долей секунды; при попадании в препятствие скорость пули уменьшается до нуля также очень быстро. При взлете ракеты ее скорость растет сначала медленно, а потом все быстрее.

Среди разнообразных ускоренных движений встречаются движения, в которых мгновенная скорость за любые равные промежутки времени увеличивается на одну и ту же величину. Такие движения называют равноускоренными. Шарик, начинающий скатываться по наклонной плоскости или начинающий свободно падать на Землю, движется равноускоренно. Заметим, что равноускоренный характер этого движения нарушается трением и сопротивлением воздуха, которые пока учитывать не будем.

Чем больше угол наклона плоскости, тем быстрее растет скорость скатывающегося по ней шарика. Еще быстрее растет скорость свободно падающего шарика (примерно на 10 м/с за каждую секунду). Для равноускоренного движения можно количественно охарактеризовать изменение скорости с течением времени, вводя новую физическую величину — ускорение.

В случае равноускоренного движения ускорением называют отношение приращения скорости к промежутку времени, за который это приращение произошло:

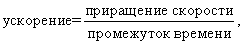
Ускорение будем обозначать буквой 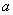. Сравнивая с соответственным выражением из § 9, можно сказать, что ускорение есть скорость изменения скорости.

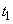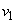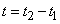Пусть в момент времени скорость была , а в момент она стала равной , так что за время приращение скорости составляет 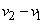. Значит, ускорение

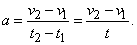
Из определения равноускоренного движения следует, что эта формула даст одно и то же ускорение, какой бы промежуток времени 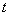ни выбрать. Отсюда видно также, что при равноускоренном движении ускорение численно равно приращению скорости за единицу времени. В СИ единица ускорения есть метр на секунду в квадрате (м/с2), т. е. метр в секунду за секунду.

Если путь и время измерены в других единицах, то и для ускорения надо принимать соответственные единицы измерения. В каких бы единицах ни выражать путь и время, в обозначении единицы ускорения в числителе стоит единица длины, а в знаменателе — квадрат единицы времени. Правило перехода к другим единицам длины и времени для ускорения аналогично правилу для скоростей. Например,

1 см/с^2=36 м/мин^2.

Если движение не является равноускоренным, то можно ввести, пользуясь той же формулой (16.1), понятие среднего ускорения. Оно охарактеризует изменение скорости за определенный промежуток времени на пройденном за этот промежуток времени участке пути. На отдельных же отрезках этого участка среднее ускорение может иметь разные значения (ср. со сказанным в § 14).

Если выбирать такие малые промежутки времени, что в пределах каждого из них среднее ускорение остается практически неизменным, то оно будет характеризовать изменение скорости на любой части этого промежутка. Найденное таким образом ускорение называют мгновенным ускорением. При равноускоренном движении мгновенное ускорение постоянно и равно среднему ускорению за любой промежуток времени.

Линейной скоростьюназывается скорость, с которой точка движется по окружности.

Формулу для величины линейной скорости можно вывести на основании следующих рассуждений.

Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2?R, за время, равное периоду Т. Взяв отношение пути 2?R ко времени T, мы получим скорость движения точки по окружности:

v = ² ⁿ ^R /_T

Но ¹/_Т = n; следовательно,

v = 2 n Rn

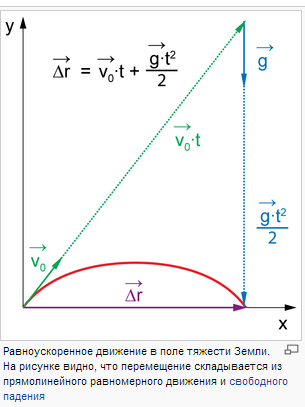
Равнозамедленное движение - движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.

Если укорение отрицательно, то модуль скорости равномерно уменьшается.

Пример гафика скорости равнозамедленного движения, здесь начальная скорость равна 2 м/с, ускорение отрицательно и модуль его равен 0,3 м/с²:

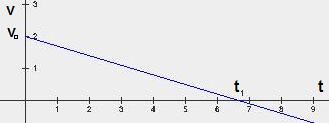
(Этот график я построил с помощью построителя графиков. Выбрал в нём вид функции "Линейная: y = k * x + b" установил k = -0.3, b = 2 и нажал кнопку "Построить график".)

Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т.е. если задать большее ускорение, то график круче пойдёт вниз.

Формула скорости равнозамедленного движения (прямолинейного):

v = v₀ - at

в этой формуле все величины являются скалярами, а не векторами. Из формулы скорости равнозамедленного движения видно, что если увеличить ускорение, то быстрее будет падать скорость. В момент времени t₁ скорость падает до нуля, а после этого момента скорость нарастает, тело движется равноускоренно, но с отрицательной скоростью.

Формула закона равнозамедленного движения:

S = S₀ + v₀t - (at²)/2

Зная среднюю скорость и время движения, можно найти пройденный путь:

Подставляя в эту формулу выражение V_ср=V/2, мы найдем путь, пройденный при равноускоренном движении из состояния покоя:

Если же мы подставим в формулу (4.1) выражениеV_ср=V₀/2, то получим путь, пройденный при торможении:

В последние две формулы входят скорости V₀ и V. Подставляя выражение V=at в формулу (4.2), а выражение V₀=at - в формулу (4.3), получим

Полученная формула справедлива как для равноускоренного движения из состояния покоя, так и для движения с уменьшающейся скоростью, когда тело в конце пути останавливается. В обоих этих случаях пройденный путь пропорционален квадрату времени движения (а не просто времени, как это было в случае равномерного движения). Первым, кто установил эту закономерность, был Г. Галилей.

Положение частицы, движущейся по окружности, можно задать углом 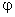, который образует радиус-вектор с каким-либо неизменным направлением, например, осью X.

Введем для движения частицы по окружности по аналогии с линейной скоростью 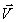угловую скорость и ускорение. Угловая скорость характеризует быстроту изменения угла поворота радиус-вектора, поэтому угловой скоростью называется производная угла поворота радиус-вектора, определяющего положение материальной точки, по времени. Пусть за время 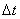точка М повернулась на угол 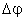(рис. 1.18), тогда угловая скорость

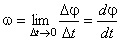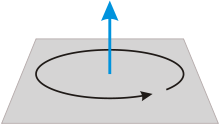
Направление вектора угловой скорости определяется по правилу правого винта. Если рукоятку винта поворачивать по направлению движения точки, то его поступательное движение покажет направление вектора угловой скорости.

При вращении частицы с постоянной по модулю скоростью угловую скорость называют также угловой частотой вращения. Она показывает, на какой угол поворачивается радиус-вектор, определяющий положение материальной точки, за единицу времени. Величина 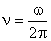дает число оборотов в единицу времени и называется частотой. Время, за которое частица совершает полный оборот, называется периодом вращения .

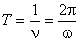Вектор угловой скорости может изменяться как за счет изменения скорости вращения тела, так и за счет поворота оси вращения в пространстве. Изменение вектора угловой скорости со временем характеризуется угловым ускорением. Пусть за время 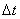вектор получает приращение 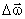. Тогда угловое ускорение определится как

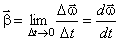Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси и направлен вдоль вектора или против него в зависимости от того, увеличивается или уменьшается угловая скорость.

Отдельные точки вращающегося тела имеют различные линейные скорости 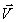, при этом скорость каждой из точек непрерывно изменяет свое направление. Можно показать, что модуль линейной скорости точки зависит от угловой скорости и от расстояния от этой точки до оси вращения. Пусть за малый промежуток времени 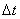тело повернулось на угол 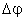. Точка, находящаяся на расстоянии от оси вращения, проходит при этом путь 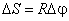. Модуль линейной скорости точки равен

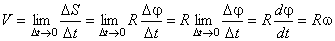Таким образом, модули линейной и угловой скорости связаны соотношением

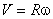Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

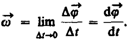
Линейная скорость точки

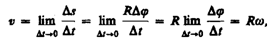
Если ( 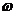= const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует 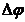= 2p, то 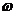= 2p/T, откуда

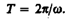
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

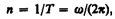
откуда

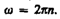
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

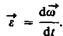
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 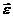сонаправлен вектору 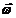(рис.8), при замедленном — противонаправлен ему (рис.9).

Тангенциальная составляющая ускорения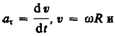

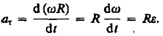
Нормальная составляющая ускорения

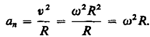
Основое уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

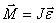
Taк как вектор скорости направлен по касательной к траектории, то вектор Dv_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

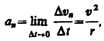
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

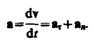
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения —быстроту изменения скорости по направлению (направлена к центру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) 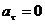, а _n = 0 — прямолинейное равномерное движение;

2) 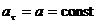, а _n = 0 — прямолинейное равнопеременное движение. При таком виде движения

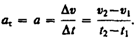
Если начальный момент времени t₁=0, а начальная скорость v₁= v₀, то, обозначив t₂= t и v₂= v , получим 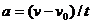, откуда

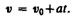
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t , найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

3) 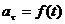, а _n = 0— прямолинейное движение с переменным ускорением;

4) 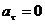, а _n = const. При 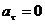скорость по модулю не изменяется, а изменяется по направлению. Из формулы a _n =v²/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;

5) 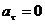, 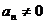— равномерное криволинейное движение;

6) 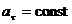, 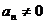— криволинейное равнопеременное движение;

7) 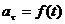, 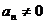— криволинейное движение с переменным ускорением.

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

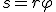. (1)

За малое время Δt точка проходит расстояние 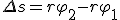, где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что 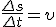и , получим

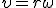. (2)

Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть 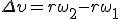, где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что 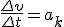и 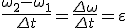, тогда касательное ускорение

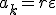. (3)

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

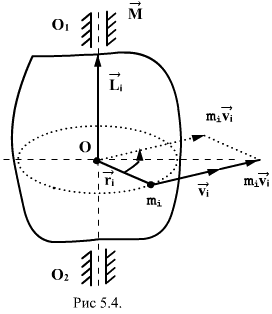
Векторное произведение радиуса-вектора 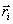материальной точки на ее импульс: 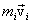называют моментом импульса 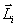, этой точки относительно точки О (рис.5.4)

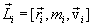. Вектор 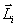иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы 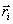и 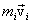и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от 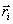к 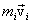происходит против часовой стрелки).

Векторную сумму моментов импульсов 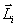всех материальных точек системы называют моментом импульса (количества движения) 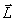системы относительно точки О:

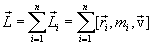
Векторы 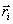и 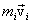взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому 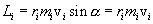. Сучетом связи линейных и угловых величин

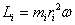
и направлен вдоль оси вращения тела в ту же сторону, что и вектор .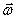

Таким образом.

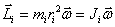
Момент импульса тела относительно оси вращения

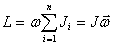
т.е.

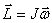
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.

Дата добавления: 2021-03-18; просмотров: 190; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!