Проверка значимости коэффициентов уравнения регрессии
Министерство образования и науки Российской Федерации
ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина»
Институт новых материалов и технологий
Кафедра «Металлургия железа и сплавов»
Оценка работы______________
Руководитель от УрФУ_________/Спирин Н.А.
Контрольная работа
На тему: «Регрессионный анализ. Проверка адекватности модели. Проверка значимости коэффициентов уравнения регрессии»
Студент Трегубова Ю.А.
Подпись ФИО
Группа НМТЗМ-102203
Екатеринбург 2021
Регрессионный анализ
Регрессионный анализ включает в себя построение уравнения регрессии, например, методом наименьших квадратов и статистическую оценку результатов. Если в регрессионном анализе расчет коэффициентов ведется теми же методами, например наименьших квадратов, то его теоретические предпосылки требуют других способов статистической оценки результатов.
При проведении регрессионного анализа примем следующие допущения:
|
|
|
· входной параметр x измеряется с пренебрежимо малой ошибкой. Появление ошибки в определении y объясняется наличием в процессе не выявленных переменных и случайных воздействий, не вошедших в уравнение регрессии;
· результаты наблюдений y1, y2,..., yi ,..., yn над выходной величиной представляют собой независимые нормально распределенные случайные величины;
· при проведении эксперимента с объемом выборки n при условии, что каждый опыт повторен m* раз, выборочные дисперсии S1 2 ,..., Si 2 ,..., Sn 2 должны быть однородны. При выполнении измерений в различных условиях возникает задача сравнения точности измерений. При этом следует подчеркнуть, что экспериментальные данные можно сравнивать только тогда, когда их дисперсии однородны. Это означает, принадлежность экспериментальных данных к одной и той же генеральной совокупности.
После того как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ состоит в следующем: проверяется значимость всех коэффициентов и устанавливается адекватность уравнения.
Проверка адекватности модели
При моделировании приходится формализовать связи исследуемого явления (процесса), из-за чего возможна потеря некоторой информации об объекте. Иногда некоторые связи не учитываются. В то же время основное требование к математической модели заключается в ее пригодности для решения поставленной задачи и адекватности процессу. Регрессионную модель называют адекватной, если предсказанные по ней значения у согласуются с результатами наблюдений. Так, построив модель в виде линейного уравнения регрессии, мы хотим, в частности, убедиться, что никакие другие модели не дадут значительного улучшения в описании предсказания значений у.
|
|
|
В основе процедуры проверки адекватности модели лежат предположения, что случайные ошибки наблюдений являются независимыми, нормально распределенными случайными величинами с нулевыми средними значениями и одинаковыми дисперсиями.
Сформулируем нуль-гипотезу Н0: «Уравнение регрессии адекватно».
Альтернативная гипотеза Н1: «Уравнение регрессии неадекватно».
Для проверки этих гипотез принято использовать F-критерий Фишера. При этом общую дисперсию (дисперсию выходного параметра) Sy2 сравнивают с остаточной дисперсией Sy ост 2. Напомним, что
,
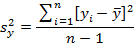
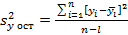где l = k + 1 — число членов аппроксимирующего полинома, а k — число факторов.
|
|
|
В дальнейшем определяется экспериментальное значение F-критерия,
F=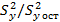 
,
который в данном случае показывает, во сколько раз уравнение регрессии предсказывает результаты опытов лучше, чем среднее
.
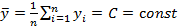Если F > Fa;m1;m2, то уравнение регрессии адекватно. Чем больше значение F превышает Fa;m1;m2 для выбранного a и числа степеней свободы m1 = n – 1, m2 = n – l, тем эффективнее уравнение регрессии.
Рассмотрим случай, когда в каждой i-й точке xi для повышения надежности и достоверности осуществляется не одно, а m* параллельных измерений (примем для простоты, что m* одинаково для каждого фактора). Тогда число экспериментальных значений величины у составит nS = n×m*. В этом случае:
1) определяется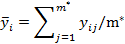 
— среднее из серии параллельных опытов при x = xi, где yij — значение параметра у при x = xi в j-м случае;
2) рассчитываются значения параметра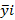 
по уравнению регрессии при x = xi;
3) рассчитывается дисперсия адекватности: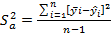 
,
где n — число значений xi ; l - число членов аппроксимирующего полинома (коэффициентов bi), для линейной зависимости l = 2;
4) определяется выборочная дисперсия Y при x = xi:
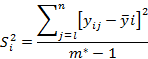
5) определяется дисперсия воспроизводимости:
|
|
|
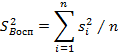
Число степеней свободы этой дисперсии равно m = n(m*–1);
6) определяется экспериментальное значение критерия Фишера
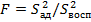
7) определяется теоретическое значение этого же критерия Fa;m1;m2, где m1 = n – l; m2= n (m*–1);
8) если F £ Fa;m1;m2, то уравнение регрессии адекватно, в противном случае — нет.
Проверка значимости коэффициентов уравнения регрессии
Проверка значимости коэффициентов выполняется по критерию Стьюдента. При этом проверяется нуль-гипотеза Н0:bi = 0, т.е. i-й коэффициент генеральной совокупности при заданном уровне значимости a отличен от нуля. Построим доверительный интервал для коэффициентов уравнения регрессии:
,
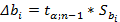где число степеней свободы в критерии Стьюдента определяется по соотношению n-l. Потеря l=k+1 степеней свободы обусловлена тем, что все коэффициенты bi рассчитываются зависимо друг от друга. Тогда доверительный интервал для Dbi коэффициента уравнения регрессии составит (bi-Dbi ; bi+Dbi). Чем уже доверительный интервал, тем с большей уверенностью можно говорить о значимости этого коэффициента. Необходимо всегда помнить рабочее правило: «Если абсолютная величина коэффициента регрессии больше, чем его доверительный интервал, то этот коэффициент значим». Таким образом, если ½bi½>½Dbi½, то bi коэффициент значим, в противном случае — нет.
Незначимые коэффициенты исключаются из уравнения регрессии, а оставшиеся коэффициенты пересчитываются заново.
Дата добавления: 2021-02-10; просмотров: 45; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!