ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕМЕ «ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ МАТРИЧНОЙ ИГРЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ имени Г.Ф. МОРОЗОВА»
Кафедра математики
Теория игр
Методические указания к выполнению расчетно-графических работ
для студентов по направлению подготовки
38.03.01 – Экономика
Воронеж 2018
УДК 512.8
Раецкая, Е. В. Теория игр [Электронный ресурс] : методические указания к выполнению расчетно-графических работ для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, С.С. Веневитина, И.В. Сапронов ; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018.
Одобрено решением учебно-методического совета
ФГБОУ ВО «ВГЛТУ» (протокол № 6 от 23.03.2018 г.)
Рецензент: д-р физ.-мат. наук, проф. кафедры
математического анализа ВГУ С.П. Зубова
Содержание
Введение……………………………………………………………………………..4
Графический метод решения матричной игры в смешанных
стратегиях …………………………………………………………………….…….5
|
|
|
2.1 Варианты индивидуальных заданий по теме «Графический метод решения матричной игры в смешанных стратегиях»………..……………...14
Библиографический список…………………………………………………….17
ВВЕДЕНИЕ
Целью изучения дисциплины «Теория игр» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, ознакомление с математическими моделями конфликтных ситуаций и методами их анализа; применению методов оптимизации, которые могут использоваться при анализе и решении широкого спектра экономических задач.
Для достижения поставленной цели решаются следующие задачи:
- закрепление теоретического материала и выработка умения решать примеры и задачи для последующего применения математических методов в различных приложениях;
- демонстрация на основе математических понятий и методов сущности научного подхода, специфики математики и ее роли как способа познания мира, общности ее понятий и представлений в решении возникающих проблем.
Для эффективного освоения дисциплины «Теория игр» у обучающегося должны быть сформированы:
- представления о необходимости доказательств, при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;
|
|
|
- понятийный аппарат по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
- умение моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат.
Студент по результатам освоения дисциплины «Теория игр» должен обладать способностью выбрать инструментальные средства для обработки данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
В результате освоения дисциплины студент должен уметь выбирать рациональные варианты действий в практических задачах принятия решений с использованием экономико-математических моделей и с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники).
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ МАТРИЧНОЙ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ
Рассмотрим игру размера 2  n с платежной матрицей
n с платежной матрицей
|
|
|
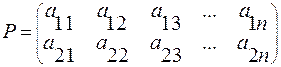
и проведем через точку (1; 0) координатной плоскости Оху прямую l , перпендикулярную оси абсцисс. После этого для каждой из стратегий 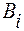 ( i = 1, 2, … , n ) проведем прямую
( i = 1, 2, … , n ) проведем прямую 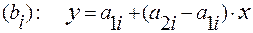 ,
,
соединяющую точку ( 0 ;  ) на оси Оу с точкой ( 1 ;
) на оси Оу с точкой ( 1 ; 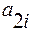 ) на прямой l . Ось Оу отвечает за стратегию
) на прямой l . Ось Оу отвечает за стратегию  , а прямая l за стратегию
, а прямая l за стратегию 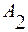 .
.
Рис. 1.1
Если игрок А применяет смешанную стратегию 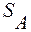 =
= 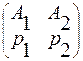 , то его выигрыш в случае, если противник применяет чистую стратегию
, то его выигрыш в случае, если противник применяет чистую стратегию 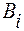 , равен
, равен
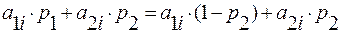 ,
,
и этому выигрышу соответствует точка М на прямой 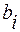 c абсциссой
c абсциссой  ( рис. 2.2 ).
( рис. 2.2 ).
Ломаная 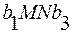 , отмеченная на чертеже ( рис. 1.2 ) жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N , в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры
, отмеченная на чертеже ( рис. 1.2 ) жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N , в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры  , а ее абсцисса
, а ее абсцисса  – вероятности применения стратегии
– вероятности применения стратегии  в оптимальной смешанной стратегии игрока А .
в оптимальной смешанной стратегии игрока А .

Рис. 1.2
Далее, непосредственно по чертежу, находим пару активных стратегий игрока В , пересекающихся в точке N (если в точке N пересекается более двух стратегий, то выбираем любые две из них). Пусть это будут стратегии 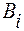 и
и 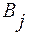 . Поскольку выигрыш игрока А , если он придерживается оптимальной стратегии, не зависит от того, с какими вероятностями игрок В применяет эти стратегии, то неизвестные
. Поскольку выигрыш игрока А , если он придерживается оптимальной стратегии, не зависит от того, с какими вероятностями игрок В применяет эти стратегии, то неизвестные 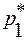 ,
, 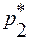 и
и  определяются из системы уравнений
определяются из системы уравнений
|
|
|
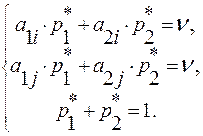
Вероятности  и
и  в оптимальной стратегии
в оптимальной стратегии
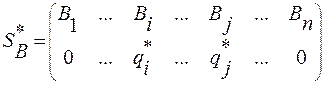
игрока В определяются из соотношения

З а м е ч а н и е. Иногда точка не является пересечением двух стратегий, а попадает на одну из прямых х = 0 или х = 1. В этом случае решением игры будут соответствующие чистые стратегии.
Для игры размера m  2 решение находится аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В , то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А , а затем найти на ней точку с минимальной ординатой.
2 решение находится аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В , то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А , а затем найти на ней точку с минимальной ординатой.
Пример. Решить графическим методом игру с платежной матрицей Р= 
Решение. Найдем  – верхнюю и
– верхнюю и 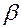 – нижнюю цены игры:
– нижнюю цены игры:



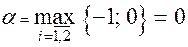 и
и 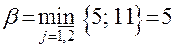 .
.
В данном случае  , то есть в игре отсутствует седловая точка и применение чистых стратегий не дает оптимального решения игры.
, то есть в игре отсутствует седловая точка и применение чистых стратегий не дает оптимального решения игры.
Платежная матрица содержит отрицательные числа, поэтому графического решения задачи перейдем к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число.
К каждому элементу исходной платежной матрицы  прибавим, например, число 2 и получим новую платежную матрицу
прибавим, например, число 2 и получим новую платежную матрицу 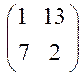 .
.
На оси абсцисс откладываем единичный отрезок 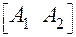 . Точка
. Точка  соответствует стратегии
соответствует стратегии  первого игрока, точка
первого игрока, точка 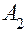 соответствует стратегии
соответствует стратегии 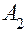 второго игрока. В точках
второго игрока. В точках  и
и 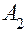 проведем оси I и II. На перпендикулярных осях I и II откладываем выигрыши при стратегиях
проведем оси I и II. На перпендикулярных осях I и II откладываем выигрыши при стратегиях  и
и 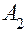 , соответственно.
, соответственно.
Пусть первый игрок придерживается стратегии  . Если 2-й игрок примет стратегию
. Если 2-й игрок примет стратегию 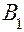 , то она дает выигрыш
, то она дает выигрыш 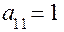 . Отложим по оси I отрезок длины
. Отложим по оси I отрезок длины 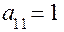 вверх от точки
вверх от точки  и обозначим полученную точку с координатами
и обозначим полученную точку с координатами 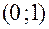 через
через 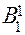 .
.
Пусть первый игрок придерживается стратегии 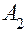 . Если 2-й игрок примет стратегию
. Если 2-й игрок примет стратегию 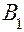 , то она дает выигрыш
, то она дает выигрыш 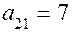 . Отложим по оси II отрезок длины
. Отложим по оси II отрезок длины 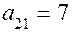 вверх от точки
вверх от точки 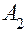 и обозначим полученную точку с координатами
и обозначим полученную точку с координатами  через
через 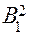 . Через точки
. Через точки 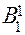
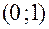 и
и 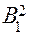
 проведем прямую
проведем прямую 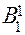
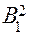 (рис. 1.3).Уравнение прямой
(рис. 1.3).Уравнение прямой 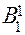
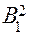 имеет вид:
имеет вид: 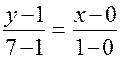 или
или 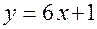 .
.

Рис. 1.3
Далее строим прямую, соответствующую применению вторым игроком стратегии 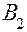 .
.
Пусть первый игрок придерживается стратегии  . Если 2-й игрок примет стратегию
. Если 2-й игрок примет стратегию 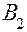 , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси I отрезок длины
. Отложим по оси I отрезок длины  вверх от точки
вверх от точки  и обозначим полученную точку с координатами
и обозначим полученную точку с координатами 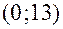 через
через  (рис. 1.4).
(рис. 1.4).
Пусть первый игрок придерживается стратегии 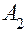 . Если 2-й игрок примет стратегию
. Если 2-й игрок примет стратегию 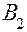 , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси II отрезок длины
. Отложим по оси II отрезок длины  вверх от точки
вверх от точки 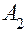 и обозначим полученную точку с координатами
и обозначим полученную точку с координатами  через
через 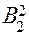 . Через точки
. Через точки 
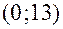 и
и 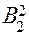
 проведем прямую
проведем прямую 
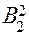 . Уравнение прямой
. Уравнение прямой 
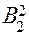 имеет вид:
имеет вид: 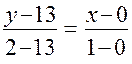 или
или 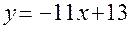 (рис. 1.4).
(рис. 1.4).

Рис. 1.4
Оптимальную стратегию 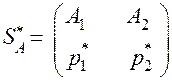 определяет точка
определяет точка 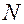 с координатами
с координатами  в которой минимальный выигрыш достигает максимума. Координаты точки
в которой минимальный выигрыш достигает максимума. Координаты точки 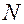 (как точки пересечения прямых
(как точки пересечения прямых 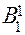
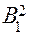 и
и 
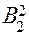 ) находятся как решение системы:
) находятся как решение системы: 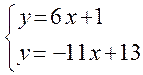 (рис. 1.5).
(рис. 1.5).
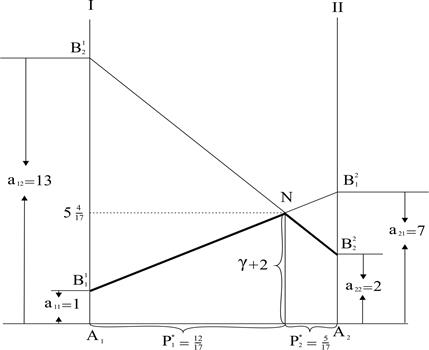
Рис. 1.5
То есть:  или
или  , откуда:
, откуда:  .
.
Определяем геометрически оптимальную стратегию второго игрока:
- меняем местами первого и второго игроков;
- вместо максимума нижней границы 
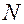
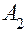 , рассматриваем минимум верхней границы.
, рассматриваем минимум верхней границы.
На оси абсцисс откладываем единичный отрезок 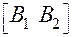 . В точках
. В точках 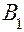 и
и 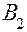 проведем оси I и II. На перпендикулярных осях I и II откладываем выигрыши при стратегиях
проведем оси I и II. На перпендикулярных осях I и II откладываем выигрыши при стратегиях 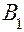 и
и 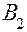 .
.
Пусть второй игрок придерживается стратегии 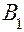 . Если 1-й игрок примет стратегию
. Если 1-й игрок примет стратегию  , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси I отрезок длины
. Отложим по оси I отрезок длины 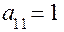 вверх от точки
вверх от точки 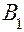 и обозначим полученную точку с координатами
и обозначим полученную точку с координатами 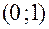 через
через  .
.
Пусть второй игрок придерживается стратегии 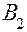 . Если 1-й игрок примет стратегию
. Если 1-й игрок примет стратегию  , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси II отрезок длины
. Отложим по оси II отрезок длины  вверх от точки
вверх от точки 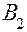 и обозначим полученную точку с координатами
и обозначим полученную точку с координатами 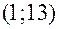 через
через 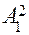 . Через точки
. Через точки 
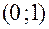 и
и 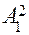
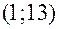 проведем прямую
проведем прямую 
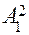 .
.
Уравнение прямой 
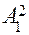 имеет вид:
имеет вид: 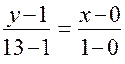 или
или 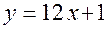 .
.
Аналогично строим прямую соответствующую применению первым игроком стратегии 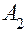 .
.
Пусть второй игрок придерживается стратегии 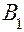 . Если 1-й игрок примет стратегию
. Если 1-й игрок примет стратегию 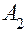 , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси I отрезок длины
. Отложим по оси I отрезок длины  вверх от точки
вверх от точки  и обозначим полученную точку с координатами
и обозначим полученную точку с координатами 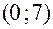 через
через  .
.
Пусть второй игрок придерживается стратегии 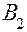 . Если 1-й игрок примет стратегию
. Если 1-й игрок примет стратегию 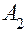 , то она дает выигрыш
, то она дает выигрыш  . Отложим по оси II отрезок длины
. Отложим по оси II отрезок длины  вверх от точки
вверх от точки 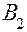 и обозначим полученную точку с координатами
и обозначим полученную точку с координатами  через
через 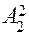 . Через точки
. Через точки 
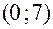 и
и 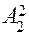
 проведем прямую
проведем прямую 
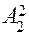 (рис. 4).
(рис. 4).
Уравнение прямой 
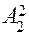 :
: 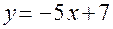 (рис. 1.6).
(рис. 1.6).

Рис. 1.6
Оптимальную стратегию 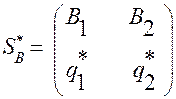 определяет точка
определяет точка  с координатами
с координатами  . Координаты точки
. Координаты точки  находятся из системы
находятся из системы
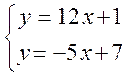
То есть:  или
или 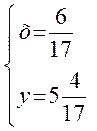 ,
,
откуда: 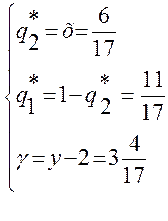 .
.
Ответ: 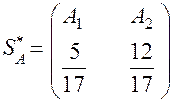 ,
,  ,
, 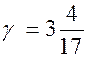 .
.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕМЕ «ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ МАТРИЧНОЙ ИГРЫ
В СМЕШАННЫХ СТРАТЕГИЯХ»
Задание. Решить графическим методом игру с платежной матрицей Р
ВАРИАНТ № 1
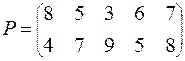 ВАРИАНТ № 2
ВАРИАНТ № 2

|
ВАРИАНТ № 3
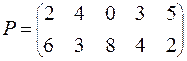 ВАРИАНТ № 4
ВАРИАНТ № 4
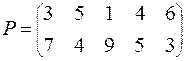
|
ВАРИАНТ № 5
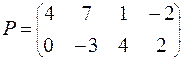
| ВАРИАНТ № 12

|
ВАРИАНТ № 6

| ВАРИАНТ № 13
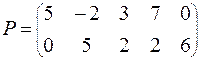
|
ВАРИАНТ № 7
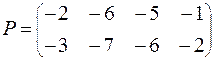
| ВАРИАНТ № 14
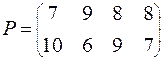
|
ВАРИАНТ № 8

| ВАРИАНТ № 15
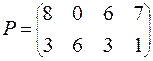
|
ВАРИАНТ № 9
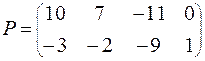
| ВАРИАНТ № 16

|
ВАРИАНТ № 10
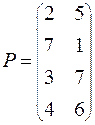
| ВАРИАНТ № 17
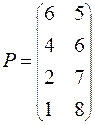
|
ВАРИАНТ № 11
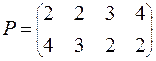
| ВАРИАНТ № 18
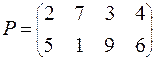
|
ВАРИАНТ № 19
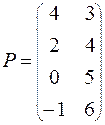
| ВАРИАНТ № 24
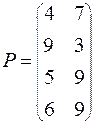
|
ВАРИАНТ № 20
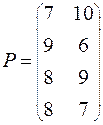
| ВАРИАНТ № 25
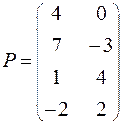
|
ВАРИАНТ № 21
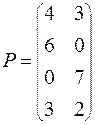
|
ВАРИАНТ № 26
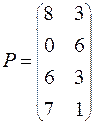
|
ВАРИАНТ № 22

| ВАРИАНТ № 27

|
ВАРИАНТ № 23
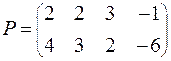
| ВАРИАНТ № 28
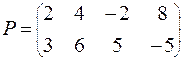
|
ВАРИАНТ № 29

| ВАРИАНТ № 30
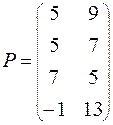
|
Библиографический список
Основная литература:
1. Конюховский, В.П. Теория игр: учебник для бакалавров / П.В. Конюховский, А.С. Малова. - М.: Издательство Юрайт, 2013. - 252 с. - Серия: Бакалавр. Базовый курс. – ЭБС «Юрайт ».
Дополнительная литература:
1.Сапронов И. В. Теория игр [Текст] : учеб. пособие : для студентов по направлению подгот. 080100 – Экономика / И. В. Сапронов, Е. О. Уточкина. Е. В. Раецкая; ВГЛТА. - Воронеж, 2013. - 204 с. - Электронная версия в ЭБС ВГЛТУ.
Дата добавления: 2021-02-10; просмотров: 71; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
