Схема решения задач на оптимизацию

Задание: выполнить задания математической разминки, изучить материал урока, решить самостоятельную работу и домашнее задание.

Урок

Тема: Примеры использования производной для нахождения наилучшего решения в прикладных задачах.

Цель: Научиться применять производную для решения прикладных задач.

Ход урока

1. Математическая разминка

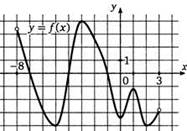
1) Дан график производной функции f(x), определенной на интервале (—3; 8). Найти количество точек максимума функции f(x), принадлежащих отрезку [—2; 7].

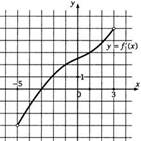
2) На рисунке изображен график функции у = f(x), определенной на интервале (-8;3). Найдите наибольшее и наименьшее значения функции.

3) На рисунке изображен график производной функции. Найдите точки, в которых функция принимает наименьшее значение.

2. Изучение нового материала

С давних времен перед человеком возникают практические проблемы выбора оптимального значения некоторой величины при определенных условиях. Как правило, в задачах подобного рода достижение некоторого результата может быть осуществлено не единственным способом и приходится отыскивать наилучший способ достижения результата.

Задачи такого характера, получившие название задачи на экстремумы или задачи на оптимизацию, возникают в самых различных областях человеческой деятельности. И их роль в жизни людей действительно очень важна. Решением таких задач занимались крупнейшие математики прошлых эпох - Евклид, Архимед, Аполлоний, Герон, Тарталья, Торричелли, Ньютон и многие другие. Ведь, несмотря на все разнообразие, их объединяет одна особенность – поиск наиболее выгодного, в определенном отношениях, наиболее экономного, наименее трудоемкого, наиболее производительного. Этот поиск кратко можно назвать поиском лучшего.

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д. Задачи подобного рода носят общее название – задачи на оптимизацию (от латинского слова optimum – “наилучший”). В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причём надо найти такое значение второй величины, при котором первая принимает своё наименьшее или наибольшее (наилучшее в данных условиях) значение. Задачи на оптимизацию решают по обычной схеме:

· составление математической модели;

· работа с моделью;

· ответ на вопрос задачи.

Схема решения задач на оптимизацию

Первый этап. Составление математической модели.

1) Проанализировав условие задачи, выделите оптимизируемую величину, т.е. величину, о наибольшем или наименьшем значении которой идёт речь. Обозначьте её буквой y (или S, V, R, t – в зависимости от фабулы).

2) Одну из участвующих в задаче неизвестных величин, через которую сравнительно нетрудно выразить оптимизируемую величину, примите за независимую переменную и обозначьте её буквой x. Установите реальные границы изменения переменной величины (в соответствии с условиями задачи), т.е. область определения для искомой оптимизируемой величины.

3) Исходя из условий задачи, выразите y через x. Математическая модель представляет собой функцию y = f(x) с областью определения X, которую нашли на втором шаге.

Второй этап. Работа с составленной моделью.

На этом этапе для функции y=f(x), x Є X найдите y_наим. или y_наиб.в зависимости от того, что требуется в условии задачи.

Третий этап. Ответ на вопрос задачи.

Здесь следует дать конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе работы с моделью.

3. Решим задачи

Задача 1. Периметр прямоугольника равен 40см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?

Решение: Выбираем независимую переменную х и выражаем через неё стороны прямоугольника. х см – длина прямоугольника, (20-х) см – ширина прямоугольника. Тогда 0< х <20;

записываем функцию S(x) =x·(20-x) =20x – x²;
находим производную S^' (x) = 20-2x;
решаем уравнение 20-2х=0. х=10.

Значит, длина и ширина равны 10 см. Какая это получается фигура? (Квадрат). S (10) = 10 (20-10) =10·10 =100 см². Ответ: 10 см.

Задача 2. Бак, имеющий вид прямоугольного параллелепипеда с квадратным основанием, должен вмещать V литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?

Решение. Первый этап. Составление математической модели. 1) Оптимизируемая величина (О.В.) — площадь поверхности бака, поскольку в задаче требуется выяснить, когда эта площадь будет наименьшей. Обозначим (О.В.) буквой S

2) Площадь поверхности зависит от измерений прямоугольного параллелепипеда. Объявим независимой переменной (Н. П.) сторону квадрата, служащего основанием бака; обозначим ее буквойx x. Ясно, что 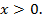Других ограничений нет, значит, 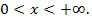Или

3) Если h— высота бака, то V=x²h, откуда находим На рис. изображен прямоугольный параллелепипед, указаны его измерения. Поверхность бака состоит из квадрата со стороной 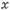и четырех прямоугольников со сторонами и . Значит, 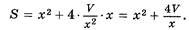Итак,

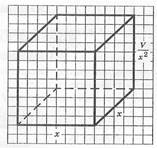
Математическая модель задачи составлена.

Второй этап. Работа с составленной моделью. На этом этапе для функции 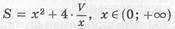надо найти 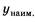. Для этого нужна производная функции: 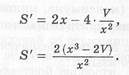На промежутке критических точек нет, а стационарная точка только одна: при 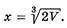Заметим, что при выполняется неравенство а при 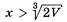выполняется неравенство Значит, 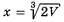— единственная стационарная точка, причем точка минимума функции на заданном промежутке, а потому, в этой точке функция достигает своего наименьшего значения.

Третий этап. Ответ на вопрос задачи. В задаче спрашивается, какой должна быть сторона основания, чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата, служащего основанием такого бака, равна Ответ: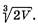

Задача 3 . Из круглого бревна вырезают балку с прямоугольным сечением наибольшей площади. Найдите размеры сечения балки, если радиус сечения бревна равен 30 см.

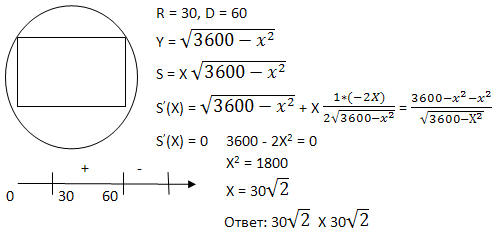
Задача 4 . Выбрать оптимальный объем производства N фирмой, функция прибыли которой может быть смоделирована зависимостью: F(q) = q² - 8q + 10.

Решение: Оптимальный объём производства есть производная от функции прибыли, т.е. N= F(q)

f '(q) = 2q - 8 = 0; q_extr = 4

При q < q_extr = 4 → F'(q) < 0 и прибыль убывает

При q > q_extr = 4 → F'(q) > 0 и прибыль возрастает

При q = 4 прибыль принимает минимальное значение.

4. Самостоятельная работа

1. Представьте число 3 в виде суммы двух положительных слагаемых так, чтобы сумма утроенного первого слагаемого и куба второго слагаемого была наименьшей.

2. Нужно огородить участок прямоугольной формы забором длиной 200м. Каковы должны быть размеры прямоугольника, чтобы его площадь была наибольшей?

3. Прибыль фирмы задана зависимостью: F(q) =4 q2 - 4q + 12.Найти оптимальный объём производства N фирмы.

Раздел математики, который изучает задачи на оптимизацию – линейное программирование.

5. Домашнее задание: § 52, № 948

Дата добавления: 2021-02-10; просмотров: 424; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!