Основные эквивалентности алгебры логики
АлгебрА логики
Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях. Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику. Особое свойство логических выражений состоит в возможности их нахождения по значениям, что и получило широкое распространение в цифровой электронике, где используются логические элементы. В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.
3.1. Основные определения
& Определение. Набор 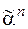 =(a1, a2,…, an), где aiÎ{0,1}, i=1,…,n, называется Булевым (двоичным) набором, при этом ai – компоненты набора (координаты вектора), n – длина набора (размерность).
=(a1, a2,…, an), где aiÎ{0,1}, i=1,…,n, называется Булевым (двоичным) набором, при этом ai – компоненты набора (координаты вектора), n – длина набора (размерность).
Каждому двоичному набору  можно сопоставить число (номер)
можно сопоставить число (номер)
 .
.
& Определение. Набор 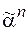 предшествует набору (или не больше)
предшествует набору (или не больше) 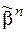 (
( 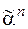
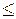
 ), если ai£bi, i=1,…,n.
), если ai£bi, i=1,…,n.
Если 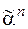
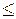
 ,
, 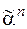 ¹
¹  , то набор
, то набор 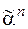 строго предшествует набору (строго меньше)
строго предшествует набору (строго меньше)  (
( 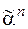 <
<  ).
).
& Определение. Наборы 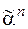 и
и  называются сравнимыми, если
называются сравнимыми, если 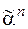
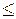
 или
или 
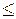
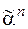 .
.
& Определение. Набор 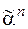 непосредственно предшествует
непосредственно предшествует  , если
, если 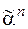 <
<  .
.
|
|
|
Пример
v Данные наборы являются сравнимыми  .
.
? Следствие. Очевидно, что если 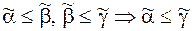 .
.
? Замечание. Не любые два набора находятся в отношении предшествования, например, наборы (0,1,1,0) и (1,0,1,0) в таком отношении не находятся, т.е. они не сравнимы.
& Определение. Функция 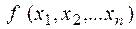 , определенная на множестве
, определенная на множестве  , и принимающая значения из множества {0, 1} называется функцией алгебры логики (булевой функцией).
, и принимающая значения из множества {0, 1} называется функцией алгебры логики (булевой функцией).
Множество всех булевых функций, зависящих от  , будем обозначать
, будем обозначать  . В произвольном случае f можно задать таблицей истинности, в которой наборы выписываются в порядке возрастания их номеров. Имея в виду такое расположение наборов функцию можно задать вектором ее значений (a1, a2,…, ak), k=2n.
. В произвольном случае f можно задать таблицей истинности, в которой наборы выписываются в порядке возрастания их номеров. Имея в виду такое расположение наборов функцию можно задать вектором ее значений (a1, a2,…, ak), k=2n.

| 
| 
| … | 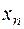
| f |
| 0 | 0 | 0 | … | 0 | 0 |
| 0 | 0 | 0 | … | 0 | 1 |
| 0 | 0 | 0 | … | 1 | 0 |
| 0 | 0 | 0 | … | 1 | 1 |
| … | … | … | … | … | … |
| 1 | 1 | 1 | … | 1 | 1 |
При n=0 функция называется ноль-местной, при этом f=0 или f=1, это функции без аргументов, т.е. константы. Одноместными называются функции от одного аргумента. Ноль- и одноместные функции можно задать следующей таблицей:
| x | f = 0 | f = 1 | f1 | f2 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
В данной таблице f=0 – тождественный ноль, f=1 – тождественная единица, f1(x)=x – тождественная функция, 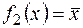 – отрицание x (не x).
– отрицание x (не x).
|
|
|
Двуместные функции:
| x1 x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 0 0 1 1 0 1 1 | 0 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 0 1 1 | 0 1 0 0 | 0 1 0 1 | 0 1 1 0 | 0 1 1 1 | 1 0 0 0 | 1 0 0 1 | 1 0 1 0 | 1 0 1 1 | 1 1 0 0 | 1 1 0 1 | 1 1 1 0 | 1 1 1 1 |
ü  .
.
ü 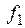 – конъюнкция:
– конъюнкция: 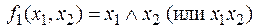 .
.
ü 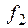 – отрицание импликации:
– отрицание импликации: 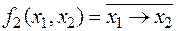 .
.
ü 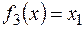 .
.
ü  – отрицание обратной импликации:
– отрицание обратной импликации: 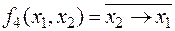 .
.
ü 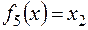 .
.
ü 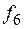 – сложение по модулю 2:
– сложение по модулю 2:  .
.
ü 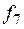 – дизъюнкция:
– дизъюнкция:  .
.
ü 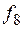 – стрелка Пирса:
– стрелка Пирса: 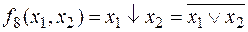 .
.
ü 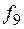 – эквивалентность:
– эквивалентность: 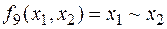 .
.
ü  .
.
ü  – обратная импликация:
– обратная импликация: 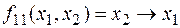 .
.
ü 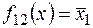 .
.
ü  – импликация:
– импликация: 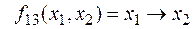 .
.
ü 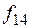 – штрих Шеффера:
– штрих Шеффера: 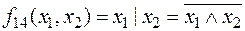 .
.
ü 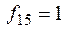 .
.
& Определение. Логические символы 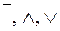 ,
, 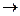 , ~,
, ~, 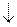 , Å,
, Å, 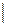 называются логическими связками.
называются логическими связками.
? Замечания
1. В формулах в отсутствие скобок приоритет применения связок возрастает в следующем порядке: ~, 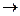 ,
, 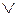 ,
, 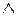 .
.
2. Связка  над одной переменной сильнее всех связок, если связка
над одной переменной сильнее всех связок, если связка  стоит над формулой, то сначала выполняется формула, затем отрицание.
стоит над формулой, то сначала выполняется формула, затем отрицание.
3. Если нет скобок, то операции ~ и 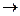 выполняются в последнюю очередь.
выполняются в последнюю очередь.
& Определение.Функция 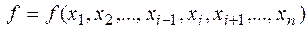 зависит существенным образом от аргумента
зависит существенным образом от аргумента 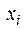 , если существуют такие значения
, если существуют такие значения 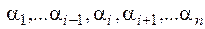 переменных
переменных 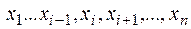 , что
, что  . Тогда переменная х i называется существенной переменной.
. Тогда переменная х i называется существенной переменной.
|
|
|
& Определение.Если для всех наборов 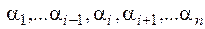
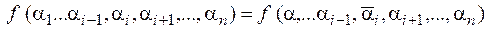 , то переменная xi называется фиктивной переменной.
, то переменная xi называется фиктивной переменной.
& Определение.Функции f1 и f2 называются равными, если f1 получается из f2 добавлением или изъятием фиктивных элементов.
Примеры
v Покажем, что  существенно зависит от
существенно зависит от 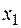 . Рассмотрим наборы (0, 1) и (1, 1), здесь
. Рассмотрим наборы (0, 1) и (1, 1), здесь 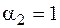 ,
, 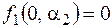 и не равно
и не равно 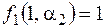 . Покажем, что
. Покажем, что  тоже существенная переменная. Рассмотрим наборы (1, 0) и (1, 1). Здесь
тоже существенная переменная. Рассмотрим наборы (1, 0) и (1, 1). Здесь 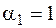 , f(1, 0)=0, но f(1, 1)=1, значит,
, f(1, 0)=0, но f(1, 1)=1, значит, 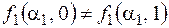 .
.
v Для функции 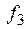 покажем, что
покажем, что  – фиктивная переменная, т.е. надо показать, что не существует наборов
– фиктивная переменная, т.е. надо показать, что не существует наборов 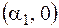 и
и  таких, что
таких, что  . Пусть
. Пусть 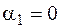 , т.е. рассмотрим наборы (0, 0) и (0, 1), f(0, 0)=f(0, 1)=0. Пусть
, т.е. рассмотрим наборы (0, 0) и (0, 1), f(0, 0)=f(0, 1)=0. Пусть 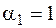 , но f(1, 0)=f(1, 1)=1. Следовательно,
, но f(1, 0)=f(1, 1)=1. Следовательно,  – фиктивная переменная.
– фиктивная переменная.
Основные эквивалентности алгебры логики
Отметим, что некоторые из представленных ниже эквивалентностей уже встречались в гл. 1.
1) коммутативность
 ;
;
2) ассоциативность
 ;
;
3) дистрибутивность
а)  ;
;
б) 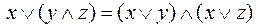 ;
;
в) 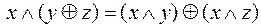 ;
;
4) правила де Моргана
а) 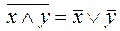 ;
;
б) 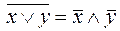 ;
;
5) правила поглощения
а) 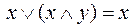 ;
;
б) 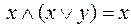 ;
;
в)  ;
;
г) 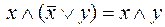 ;
;
6) элементарные преобразования
а) 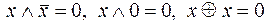 ;
;
б) 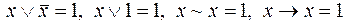 ;
;
в)  ;
;
г)  ;
;
д) 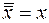 ;
;
7) выражение функций через 
|
|
|
а)  ;
;
б) 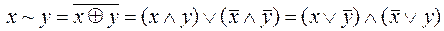 ;
;
в) 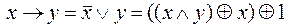 ;
;
г)  ;
;
д)  .
.
Пример
v Доказать эквивалентность формул:
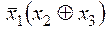 и
и 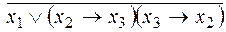 .
.
Докажем эквивалентность данных формул с помощью таблицы истинности.
| x1 | x2 | x3 | 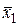
| 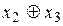
| 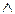
| 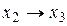
| 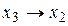
| 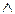
| 
| 
|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
В первых трех столбцах приводятся значения трех переменных, в последующих двух высчитываются значения элементов первой формулы (отрицание и сложение по модулю 2), в следующем столбце приведены окончательные значения первой формулы. Далее подобным образом рассчитываются значения второй формулы. Эквивалентность обеих формул очевидна благодаря совпадению значений шестого и одиннадцатого столбца.
v Преобразовать выражение
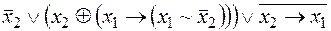 .
.
Применяя основные эквивалентности, получим:

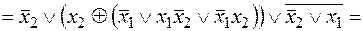
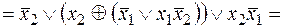
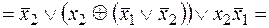

 .
.
Двойственные функции
& Определение. Функция 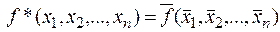 называется двойственной функцией к функции
называется двойственной функцией к функции 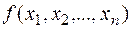 .
.
Если  , то
, то 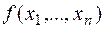 называется самодвойственной.
называется самодвойственной.
& Утверждение.Для получения двойственной функции с помощью таблицы истинности необходимо инвертировать  (заменить 0 на 1, 1 – на 0), после чего перевернуть столбец значений функции.
(заменить 0 на 1, 1 – на 0), после чего перевернуть столбец значений функции.
Пример
v Найдем двойственную функцию к 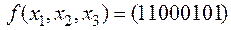 . Приведем таблицу истинности функции f и двойственной к ней.
. Приведем таблицу истинности функции f и двойственной к ней.
| x1 | x2 | x3 | 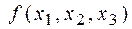
| 
|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
v Соответствие некоторых элементарных функций
| f | 0 | 1 | x | 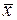
| 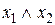
| 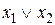
|
| f* | 1 | 0 | x | 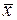
| 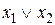
| 
|
v Построим формулу, реализующую f*, если 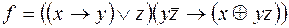 . Покажем, что она эквивалентна формуле
. Покажем, что она эквивалентна формуле  . Найдем
. Найдем 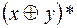 и
и 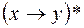 по таблице:
по таблице:
| x | y | 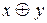
| 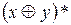
| 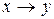
| 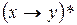
|
| 0 0 1 1 | 0 1 0 1 | 0 1 1 0 | 1 0 0 1 | 1 1 0 1 | 0 1 0 0 |
Из таблицы видно, что 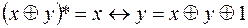 ,
,  .
.
По принципу двойственности
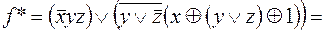

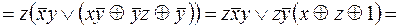
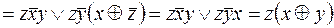 .
.
v Покажем по определению, что функция 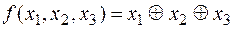 является самодвойственной:
является самодвойственной:
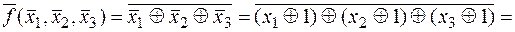
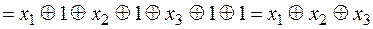 .
.
После преобразований получили начальное выражение.
? Замечание. Из определения двойственности следует, что
 .
.
& Теорема. Принцип двойственности: двойственной к формуле 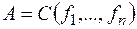 является формула
является формула 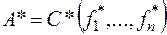 .
.
Пусть формула содержит только логические связки 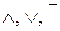 . Тогда для получения
. Тогда для получения 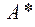 из A необходимо заменить 0 на 1, 1 на 0,
из A необходимо заменить 0 на 1, 1 на 0, 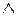 на
на 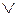 ,
, 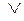 на
на 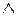 .
.
Из принципа двойственности вытекает, что
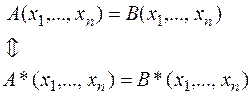 ,
,
т.е. доказывать необходимо только половину тождеств, вторая половина получается из принципа двойственности.
Пример
v
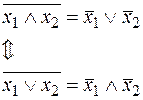 .
.
Обозначим 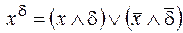 , где d равен либо 0, либо 1. Тогда
, где d равен либо 0, либо 1. Тогда
 ,
, 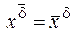 .
.
Тогда
| x\δ | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
& Лемма о несамодвойственной функции.Подстановкой функций 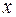 и
и  в несамодвойственную функцию можно получить одну из констант.
в несамодвойственную функцию можно получить одну из констант.
Доказательство. Пусть 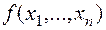 – несамодвойственная функция. Тогда существует набор
– несамодвойственная функция. Тогда существует набор 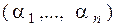 , для которого
, для которого 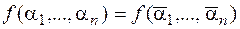 . Построим функцию
. Построим функцию  , заменив единицы в
, заменив единицы в 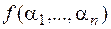 на
на 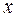 , а нули – на
, а нули – на  . Так как
. Так как  , то
, то  . Заметим, что
. Заметим, что  .
.
Тогда

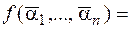
 ,
,
т.е. 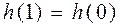 . Следовательно, функция
. Следовательно, функция  есть одна из констант.
есть одна из констант.
3.2. Представление булевых функций
& Определение. Конъюнктивным одночленом от переменных 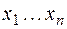 называется конъюнкция этих переменных или их отрицаний. Аналогично определен дизъюнктивный одночлен.
называется конъюнкция этих переменных или их отрицаний. Аналогично определен дизъюнктивный одночлен.
& Определение. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конъюнктивных одночленов  , где
, где  – конъюнктивные одночлены, причем в любом из
– конъюнктивные одночлены, причем в любом из  каждая переменная встречается не более одного раза, т.е. в него от каждой пары
каждая переменная встречается не более одного раза, т.е. в него от каждой пары 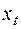 или
или  входит только 1 представитель.
входит только 1 представитель.
& Определение. Конъюнктивной нормальной формой (КНФ) называется конъюнкция дизъюнктивных одночленов с теми же условиями 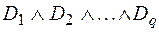 , где
, где 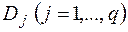 – дизъюнктивный одночлен.
– дизъюнктивный одночлен.
ДНФ (КНФ) также называются указанные выражения при 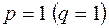 . Всякая формула обладает как ДНФ, так и КНФ, которых неограниченно много, но среди них существует уникальная форма, которая является единственной для данной формулы.
. Всякая формула обладает как ДНФ, так и КНФ, которых неограниченно много, но среди них существует уникальная форма, которая является единственной для данной формулы.
Снова воспользуемся разложением 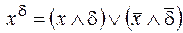 , где d равен либо 0, либо 1.
, где d равен либо 0, либо 1.
Пусть 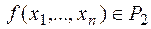 . Тогда для любого m:
. Тогда для любого m: 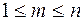 допустимо представление:
допустимо представление:
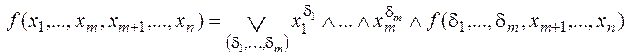 ,
,
где дизъюнкция берется по всем наборам из 0 и 1. Такое представление называется разложением функции f по переменным
x1, ..., xn.
Разложение функции по одной переменной можно представить в следующем виде
 .
.
Разложение функции по двум переменным:
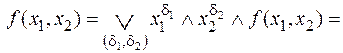
 .
.
Пример
v Если 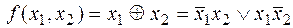 .
.
Разложение по всем n переменным
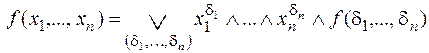 .
.
При 
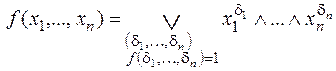 . (3.1)
. (3.1)
& Определение. Разложение (3.1) называется совершенной дизъюнктивной нормальной формой (СДНФ) представления функции f(x1,…,xn).
Пример
v Представить в виде СДНФ функцию  .
.
Для получения разложения в СДНФ, согласно (3.1), из таблицы истинности выбираются только те строки, где f=1, их количество определяет количество конъюнктивных одночленов в итоговой дизъюнкции. Запишем таблицу истинности для импликации:
| x1 | x2 | f |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Каждый конъюнктивный одночлен («слагаемое») состоит из конъюнкции всех переменных функции, если в таблице xi=0, в конъюнкцию включается 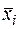 , и, наоборот: при xi=1, записывается xi. Итоговое представление функции импликации в СДНФ имеет вид:
, и, наоборот: при xi=1, записывается xi. Итоговое представление функции импликации в СДНФ имеет вид:
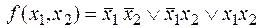 .
.
Для проверки равносильности данного разложения исходному выражению преобразуем его:
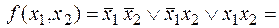
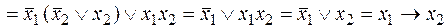 .
.
В результате получили исходную функцию.
v Представить в виде СДНФ функцию 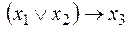 .
.
С помощью элементарных преобразований приведем функцию к виду:
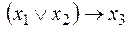
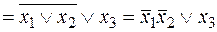 .
.
Каждый конъюнктивный одночлен в СДНФ должен содержать все переменные 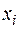 , i =1,…,n, где n – общее количество переменных в выражении. Для выполнения этого условия домножим каждое слагаемое, в сомножителях которого не хватает i-той переменной, на
, i =1,…,n, где n – общее количество переменных в выражении. Для выполнения этого условия домножим каждое слагаемое, в сомножителях которого не хватает i-той переменной, на  , так как
, так как  , то данное преобразование позволит получить эквивалентное выражение:
, то данное преобразование позволит получить эквивалентное выражение:

 .
.
Пусть  . СДНФ для f*
. СДНФ для f*
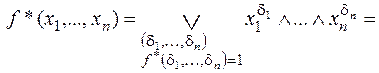
 .
.
Согласно теореме двойственности

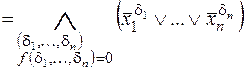 . (3.2)
. (3.2)
& Определение.Разложение (3.2) называется совершенной конъюнктивной нормальной формой (СКНФ).
Примеры
v Зададим функцию таблицей и найдем ее разложение в СКНФ:
| x1 | x2 | f |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Для получения разложения в СКНФ, согласно (3.2), из таблицы истинности выбираем только те строки, в которых f=0, каждая из них преобразуется в дизъюнктивный одночлен в итоговой конъюнкции. Каждый дизъюнктивный одночлен состоит из всех переменных функции; если в таблице xi=0, в сумму включается xi, и, наоборот: при xi=1, записывается 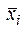 . Конечное представление заданной функции в СКНФ имеет вид:
. Конечное представление заданной функции в СКНФ имеет вид:
 .
.
Заметим, что, применив преобразования с помощью основных эквивалентностей, можно получить представление функции в СДНФ:
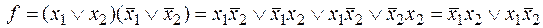 .
.
v Разложение в СКНФ функции импликации, согласно (3.2), будет иметь вид
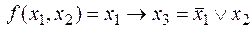 .
.
v Представим функцию в СКНФ с помощью элементарных преобразований 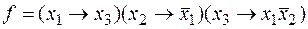 .
.
Приведем функцию к виду:
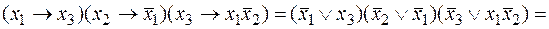
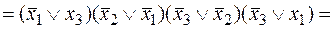
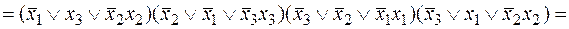

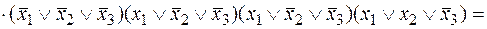
 .
.
3.3. Полнота и замкнутость
& Определение.Система функций 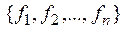 из P2 называется (функционально) полной, если любая булева функция может быть записана в виде формулы через функции этой системы.
из P2 называется (функционально) полной, если любая булева функция может быть записана в виде формулы через функции этой системы.
Примеры
v Само множество 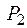 – система полная;
– система полная;
v 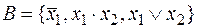 – система полная;
– система полная;
v 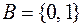 – система не полная;
– система не полная;
v 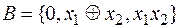 – система не полная.
– система не полная.
& Лемма (достаточное условие полноты). Пусть система
U={f1, f2, ..., f s, ...} полна в Р2. Пусть B={g1, g2, ..., g k, ...} – некоторая система из Р2, причем любая функция 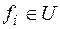 может быть выражена формулой над B, тогда система B полна в Р2.
может быть выражена формулой над B, тогда система B полна в Р2.
Пример
v Система {x1Úx2,  } – полна в P2. Возьмем в качестве полной в Р2 системы U={
} – полна в P2. Возьмем в качестве полной в Р2 системы U={ 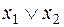 ,
, 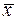 ,
,  }, B={
}, B={ 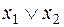 ,
, 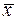 }. Надо показать, что
}. Надо показать, что  представляется формулой над B. Действительно, по правилу де Моргана получим:
представляется формулой над B. Действительно, по правилу де Моргана получим:  =
= 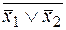 .
.
v Система {  } полна в Р2. Для доказательства возьмем в качестве полной в Р2 системы U={
} полна в Р2. Для доказательства возьмем в качестве полной в Р2 системы U={  ,
, 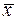 } и выразим
} и выразим  и
и 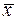 через
через  :
: 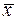 =
=  ,
,  =
=  =
= 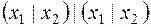 .
.
& Теорема Жегалкина. Каждая функция из 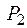 может быть выражена единственным образом при помощи полинома по модулю 2 – полинома Жегалкина:
может быть выражена единственным образом при помощи полинома по модулю 2 – полинома Жегалкина:
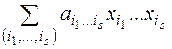 .
.
Доказательство. Заметим, что различных булевых функций от n переменных 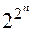 штук. При этом конъюнкций вида
штук. При этом конъюнкций вида  существует ровно
существует ровно 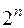 , так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, т.е. существует
, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, т.е. существует 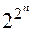 различных полиномов Жегалкина от n переменных.
различных полиномов Жегалкина от n переменных.
Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, т.е. с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, т.е. нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
Пример
v Получить полином Жегалкина функции

с помощью метода неопределенных коэффициентов.
Метод неопределенных коэффициентов использует следующее представление функции двух аргументов
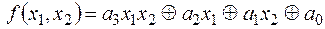 .
.
Найдем все коэффициенты с помощью таблицы истинности:
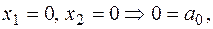
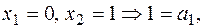

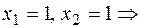
 .
.
Следовательно,
 .
.
Заметим, что для функции от трех переменных полином Жегалкина в общем виде запишется так:
 ,
,
таким образом, увеличение количества аргументов на один значительно усложняет применение метода неопределенных коэффициентов.
v Получить полином Жегалкина функции
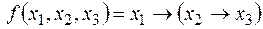
с помощью метода элементарных преобразований.
Применим основные эквивалентности для преобразования данной функции

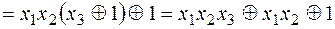 .
.
v Получить полином Жегалкина функции
f=(10011110)
с помощью треугольника Паскаля.
Для получения полинома Жегалкина построим треугольник Паскаля по данной функции. По единицам его левой стороны и определяются элементы многочлена Жегалкина.
| N | x1x2x3 | f | Треугольник Паскаля |
| 1 x3 x2 x2x3 x1 x1x3 x1x2 x1x2x3 | 000 001 010 011 100 101 110 111 | 1 0 0 1 1 1 1 0 | 1 0 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 0 1 |
Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю 2 для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать 6 слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем  . Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
Тогда 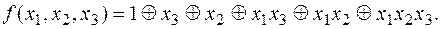
& Определение. Функция 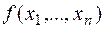 , полином Жегалкина для которой имеет следующий линейный относительно переменных вид:
, полином Жегалкина для которой имеет следующий линейный относительно переменных вид:
 ,
,
называется линейной.
& Определение. Суперпозицией булевых функций

в булеву функцию 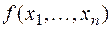 называется новая булева функция, полученная из функции
называется новая булева функция, полученная из функции 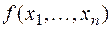 подстановкой вместо (всех или некоторых) аргументов
подстановкой вместо (всех или некоторых) аргументов  функций
функций  соответственно, т.е.
соответственно, т.е.
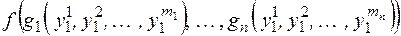 .
.
Пример
v 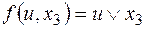 ,
,  ,
,
тогда 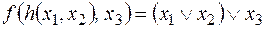 .
.
& Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.
Доказательство. Пусть 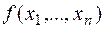 – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение
– нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение  . Будем считать для простоты, что
. Будем считать для простоты, что 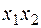 в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде
в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде

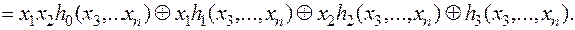
Функция 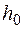 не есть тождественный ноль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением
не есть тождественный ноль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением 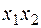 . Тогда существует набор
. Тогда существует набор 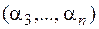 из 0 и 1, для которого
из 0 и 1, для которого  . Пусть
. Пусть 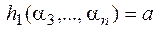 ,
, 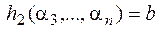 ,
, 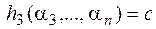 . Тогда
. Тогда
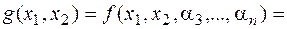
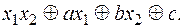
Построим функцию:



где 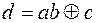 . Если d=0, то
. Если d=0, то 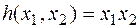 . Если d=1, то
. Если d=1, то 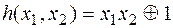 и тогда
и тогда 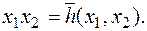 Лемма доказана.
Лемма доказана.
Пусть M – некоторое подмножество функций из P2.
& Определение. Замыканием M называется множество всех булевых функций, представимых в виде формул через функции множества M. Замыкание обозначается [M].
? Замечание. Замыкание инвариантно относительно операций введения и удаления фиктивных переменных.
Пример
v M=P2, [M]=P2.
& Определение. Класс (множество) M называется функционально замкнутым, если [M]=M.
Примеры
v Класс M=P2 функционально замкнут.
v Класс {1, x1Åx2} не замкнут; его замыканием будет класс линейных функций:
[{1, 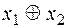 }]={
}]={ 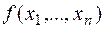 =
= 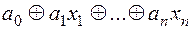 }.
}.
Действительно, по определению формулы над М, функция  , где f – есть сумма по модулю 2, G1 – функция
, где f – есть сумма по модулю 2, G1 – функция 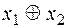 , будет формулой над М:
, будет формулой над М: 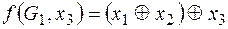 .
.
? Следствие. M является полной системой, если [M]=P2.
& Определение. 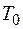 называется классом всех булевых функций
называется классом всех булевых функций 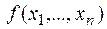 , сохраняющих константу 0, т.е. функций, для которых выполняется равенство
, сохраняющих константу 0, т.е. функций, для которых выполняется равенство  . При добавлении в функцию фиктивной переменной равенство не меняется.
. При добавлении в функцию фиктивной переменной равенство не меняется.
Примеры
v  .
.
v 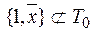 .
.
? Следствие. Количество функций 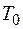
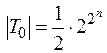 ,
,
где n – число переменных. Так как в первой строке таблицы истинности для  всегда содержится 0, то данному условию удовлетворяет половина всех булевых функций.
всегда содержится 0, то данному условию удовлетворяет половина всех булевых функций.
& Определение. 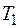 называется классом всех булевых функций
называется классом всех булевых функций 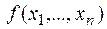 , сохраняющих константу 1, т.е. функций, для которых выполняется равенство
, сохраняющих константу 1, т.е. функций, для которых выполняется равенство 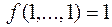 .
.
Класс вместе с любой функцией содержит равную ей функцию.
Примеры
v 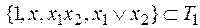 .
.
v  .
.
? Следствие. Класс 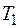 состоит из функций двойственных классу
состоит из функций двойственных классу 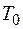 , что следует из определения, поэтому все свойства класса
, что следует из определения, поэтому все свойства класса 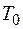 переносятся на класс
переносятся на класс 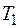 . Количество функций
. Количество функций 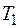
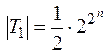 .
.
& Утверждение. Классы 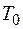 и
и 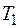 являются замкнутыми.
являются замкнутыми.
& Определение. S называется классом всех самодвойственных функций, как отмечалось выше, если  , т.е.
, т.е. 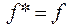 .
.
& Утверждение. Класс S является замкнутым.
Примеры
v 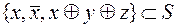 .
.
v  .
.
Так как  , на наборах
, на наборах 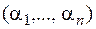 и
и 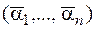 функция принимает противоположные значения (определяется половиной комбинаций xi), поэтому число самодвойственных функций равно
функция принимает противоположные значения (определяется половиной комбинаций xi), поэтому число самодвойственных функций равно
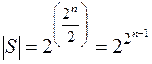 .
.
? Замечание. Если функция самодвойственная, то ее отрицание – также самодвойственная функция.
Пример
v Функция 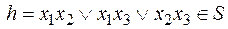 , так как
, так как

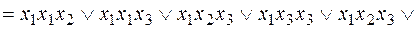

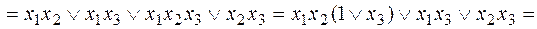
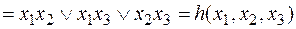 .
.
& Определение. Функция 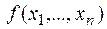 называется монотонной, если для любых 2х наборов
называется монотонной, если для любых 2х наборов  таких, что
таких, что  выполняется неравенство
выполняется неравенство
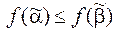 .
.
& Утверждение. Класс М – монотонных функций является замкнутым.
Примеры
v Монотонные функции: 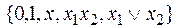 .
.
v Функции  – не монотонны.
– не монотонны.
Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число для больших n сосчитать не удается.
Подсчет числа монотонных функций представляет собой известную проблему Дедекинда. Точные значения количества монотонных функций  известны только для малых значений n.
известны только для малых значений n.
| n | 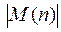
|
| 0 | 2 |
| 1 | 3 |
| 2 | 6 |
| 3 | 20 |
| 4 | 168 |
| 5 | 7581 |
| 6 | 7 828 354 |
| 7 | 2 414 682 040 998 |
| 8 | 56 130 437 228 687 557 907 788 |
Известно, что  . Приведем рассуждения, обосновы-вающие нижнюю оценку числа монотонных функций. Рассмотрим случай, когда n четно. На всех наборах, где количество нулей превышает количество единиц, значение функции положим равным 0. Если количество единиц набора превышает количество нулей, значение функции положим равным 1. На оставшихся наборах, где нулей и единиц поровну, зададим значение функции произвольным образом. Все такие функции будут монотонными, и их количество равно
. Приведем рассуждения, обосновы-вающие нижнюю оценку числа монотонных функций. Рассмотрим случай, когда n четно. На всех наборах, где количество нулей превышает количество единиц, значение функции положим равным 0. Если количество единиц набора превышает количество нулей, значение функции положим равным 1. На оставшихся наборах, где нулей и единиц поровну, зададим значение функции произвольным образом. Все такие функции будут монотонными, и их количество равно 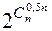 . Заметим, что таких функций «много», если сравнить с общим количеством булевых функций n переменных. Кроме того, верхняя оценка близка к нижней. Для нечетного n возможна аналогичная конструкция.
. Заметим, что таких функций «много», если сравнить с общим количеством булевых функций n переменных. Кроме того, верхняя оценка близка к нижней. Для нечетного n возможна аналогичная конструкция.
Таким образом известны следующие нижняя и верхняя оценки числа монотонных функций:
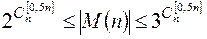 .
.
? Замечание. Если функция 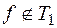 и не равна нулю, то она не монотонна.
и не равна нулю, то она не монотонна.
& Лемма о немонотонной функции. Суперпозицией констант 0 и 1, тождественной функции и немонотонной функции можно получить отрицание.
Доказательство. Пусть 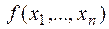 – немонотонная функция. Тогда существуют наборы
– немонотонная функция. Тогда существуют наборы  и
и  , для которых
, для которых 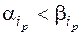 но
но 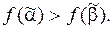 Пусть i1, …, ik есть все те номера аргументов, для которых
Пусть i1, …, ik есть все те номера аргументов, для которых 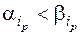 , p=1, …, k. На всех остальных аргументных местах j имеем
, p=1, …, k. На всех остальных аргументных местах j имеем 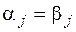 . В выражении
. В выражении 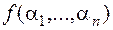 заменим нули на местах i1, …, ik на x. В результате получим функцию g(x), для которой g(0)=f(
заменим нули на местах i1, …, ik на x. В результате получим функцию g(x), для которой g(0)=f( 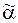 )=1 и g(1)=f(
)=1 и g(1)=f( 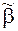 )=0. Функция g(x) является отрицанием.
)=0. Функция g(x) является отрицанием.
? Замечание. Класс L – линейных функций является замкнутым.
Примеры
v 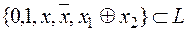 .
.
v 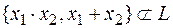 .
.
Так как линейная функция n аргументов может содержать максимум n+1 слагаемое, то количество различных линейных функций равно
 .
.
Отметим, что линейные функции бывают 4 типов:
1)  , где n – четное;
, где n – четное;  ,
, 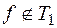 ,
,  .
.
2)  , где n – нечетное;
, где n – нечетное;  ,
, 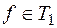 ,
,  .
.
3)  , где n – четное;
, где n – четное;  ,
, 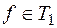 ,
,  .
.
4)  , где n –нечетное;
, где n –нечетное;  ,
, 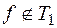 ,
,  .
.
Линейные функции практически все не монотонны, кроме функций: 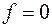 ,
,  ,
, 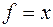 .
.
Заметим, что константы линейны, монотонны и не самодвойственны.
Описанные замкнутые классы не тождественны и не полны, что следует из таблицы (называемой критериальной):
| T0 | T1 | S | M | L | |
| 0 | + | – | – | + | + |
| 1 | – | + | – | + | + |
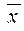
| – | – | + | – | + |
& Теорема (о функциональной полноте). Для того чтобы система функций 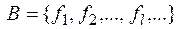 была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из 5 замкнутых классов T0, T1, S, M, L.
была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из 5 замкнутых классов T0, T1, S, M, L.
Доказательство. Необходимость. Докажем необходимость этого условия. Пусть система  полна в Р2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T0, T1, L, S, M. Докажем от противного, пусть
полна в Р2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T0, T1, L, S, M. Докажем от противного, пусть 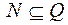 , очевидно,
, очевидно,  , но
, но 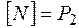 , т.к. N – полна в Р2, отсюда
, т.к. N – полна в Р2, отсюда 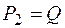 , но это не так. Необходимость доказана.
, но это не так. Необходимость доказана.
Достаточность. Пусть  , где
, где 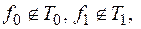
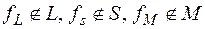 . Покажем, что суперпозицией функций системы F можно получить полную систему G={
. Покажем, что суперпозицией функций системы F можно получить полную систему G={ 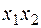 ,
, 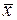 }.
}.
1. Пусть g(x)=f0(x, …, x). Тогда g(0)=f(0, …, 0)=1. Далее возможны два случая:
I) g(1)=1. Тогда g(x)º1. Функция
h(x)=f1(g(x), …, g(x))=f1(1, …, 1)=0, т.е. h(x)º0.
Получили константы 0 и 1;
II) g(1)=0. Тогда g(x)= 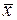 . По лемме о несамодвойственной функции суперпозицией над {fs,
. По лемме о несамодвойственной функции суперпозицией над {fs, 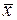 } можно получить одну из констант, например, 0. Тогда f0(0, …, 0)=1 есть другая константа.
} можно получить одну из констант, например, 0. Тогда f0(0, …, 0)=1 есть другая константа.
В обоих случаях получили обе константы.
2. По лемме о немонотонной функции суперпозицией над {fm, 0, 1} можно получить отрицание.
3. По лемме о нелинейной функции суперпозицией над {fL, 1, 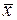 } можно получить конъюнкцию. Теорема доказана.
} можно получить конъюнкцию. Теорема доказана.
? Следствие. Всякий замкнутый класс функций из Р2, не совпадающий с Р2 содержится, по крайней мере, в одном из замкнутых классов T0, T1, L, S, M.
Действительно, если N не является подмножеством Q, то [N]=P2, что неверно.
Пример
v Определить полноту системы булевых функций
{0, 1, 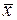 ,
, 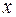 ,
, 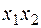 }. Составим критериальную таблицу:
}. Составим критериальную таблицу:
| T0 | T1 | S | M | L | |
| 0 | + | – | – | + | + |
| 1 | – | + | – | + | + |
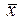
| – | – | + | – | + |
| x | + | + | + | + | + |
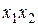
| + | + | – | + | – |
Из таблицы видно, что для любого класса всегда есть функция из данной системы, которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус». Итак, данная система полна.
& Определение.Система функций {f1, ..., f s, ...} называется базисом в Р2, если она полна в Р2, но любая ее подсистема не будет полной.
Примеры
v Определить полноту системы булевых функций и выделить базисы { 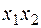 , 0, 1,
, 0, 1, 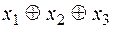 }
}
| Т0 | Т1 | L | M | S | |
| x1x2 | + | + | – | + | – |
| 0 | + | – | + | + | – |
| 1 | – | + | + | + | – |
| x1Åx2Åx3 | + | + | + | – | + |
Из таблицы видно, что система функций полна, помимо того, какую бы функцию из системы ни удалить, система станет неполной, действительно,  ,
, 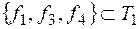 ,
, 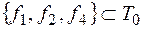 ,
,  . Таким образом, вся система функций {
. Таким образом, вся система функций { 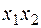 , 0, 1,
, 0, 1, 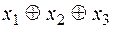 } – базис.
} – базис.
v Система 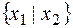 – полна в Р2.
– полна в Р2. 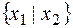 =
= 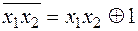 .
.
| Т0 | Т1 | L | M | S | |
| x1|x2 | – | – | – | – | – |
v Рассмотрим полноту системы {0, 1, 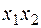 ,
, 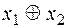 }
}
| Т0 | Т1 | L | M | S | |
| 0 | + | – | + | + | – |
| 1 | – | + | + | + | – |
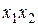
| + | + | – | + | – |
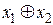
| + | – | + | – | – |
Согласно критериальной таблице система является полной.
& Теорема о достаточности четырех функций. Из любой полной в Р2 системы функций можно выделить полную подсистему, состоящую не более чем из четырех функций.
Доказательство.Пусть  – полная система функций, тогда она не лежит целиком ни в одном из классов T0, T1, L, M, S. Следовательно, в системе есть функции
– полная система функций, тогда она не лежит целиком ни в одном из классов T0, T1, L, M, S. Следовательно, в системе есть функции 
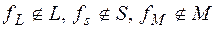 . Система
. Система 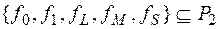 и образует полную систему в Р2. Рассмотрим функцию f0: f0(0, ..., 0)=1. Если
и образует полную систему в Р2. Рассмотрим функцию f0: f0(0, ..., 0)=1. Если
f0(1, ..., 1)=0, то 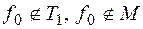 , тогда
, тогда 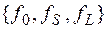 – полная система из трех функций. Если f0(1, ..., 1)=1, то
– полная система из трех функций. Если f0(1, ..., 1)=1, то 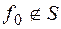 и
и  образует полную систему из четырех функций.
образует полную систему из четырех функций.
Пример, приведенный выше, показывает, что число 4 в общем случае уменьшить нельзя, из полной системы { 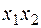 , 0, 1,
, 0, 1, 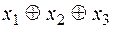 } нельзя выделить полную подсистему.
} нельзя выделить полную подсистему.
Примеры
v Выясним, полна ли система  .
.
Составим критериальную таблицу, очевидно 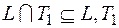 . Чтобы показать, что
. Чтобы показать, что 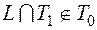 , достаточно найти одну функцию, которая принадлежит
, достаточно найти одну функцию, которая принадлежит  и не принадлежит
и не принадлежит 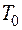 . Возьмем
. Возьмем 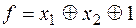 , удовлетворяющую требуемым условиям. Если
, удовлетворяющую требуемым условиям. Если 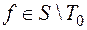 , то f(0, ..., 0) = 1, f(1, ..., 1) = 0, следовательно,
, то f(0, ..., 0) = 1, f(1, ..., 1) = 0, следовательно,  ,
, 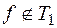 . Рассмотрим функцию
. Рассмотрим функцию  , набор ее значений (11101000),
, набор ее значений (11101000), 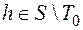 , но
, но  . Следовательно, критериальная таблица имеет вид
. Следовательно, критериальная таблица имеет вид
| Т0 | Т1 | L | M | S | |
L  T1 T1
| – | + | + | – | – |
| S\T0 | – | – | – | + | + |
и А – полная система функций.
v Выясним, полна ли система 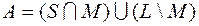 .
.
Составим таблицу, очевидно  , при этом
, при этом
f(0, ..., 0) = 0, f(1, ..., 1) = 1, значит  и
и 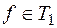 . Чтобы показать, что функции
. Чтобы показать, что функции  не линейны, достаточно найти одну функцию, которая принадлежит
не линейны, достаточно найти одну функцию, которая принадлежит  и не принадлежит
и не принадлежит  . Возьмем
. Возьмем 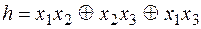 , удовлетворяющую требуемым условиям. Если
, удовлетворяющую требуемым условиям. Если 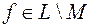 , то найдем функцию,
, то найдем функцию,  :
: 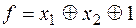 , функцию,
, функцию, 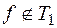 :
: 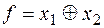 , причем обе эти функции не самодвойственны. Следовательно, критериальная таблица имеет вид
, причем обе эти функции не самодвойственны. Следовательно, критериальная таблица имеет вид
| Т0 | Т1 | L | M | S | |

| + | + | – | + | + |

| – | – | + | – | – |
и А – полная система функций.
v Рассмотрим систему
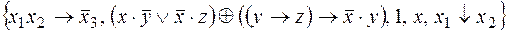 ,
,
прежде чем исследовать ее на полноту, преобразуем вторую функцию:
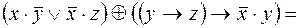
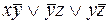 .
.
Теперь составим критериальную таблицу, из которой видно, что система является полной, а значит, из нее можно выделить базисы.
| Т0 | Т1 | L | M | S | ||
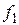
| 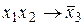
| – | – | – | – | – |

| 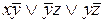
| + | – | – | – | – |
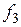
| 1 | – | + | + | + | – |
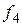
| 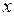
| + | + | + | + | + |
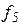
| 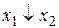
| – | – | – | – | – |
Для этого составим КНФ, формируя дизъюнктивные одночлены из функций, которым соответствуют минусы в каждом столбце, и преобразуем ее в ДНФ:
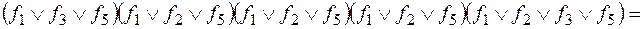
 .
.
Полученная ДНФ содержит в себе в качестве конъюнктивных одночленов базисы исходной системы:
 .
.
Анализируя критериальную таблицу можно убедиться в правильности найденных базисов системы.
Дата добавления: 2021-02-10; просмотров: 962; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
