Свойства действий над множествами
ДИСКРЕТНАЯ МАТЕМАТИКА
Уфа 2019
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Уфимский государственный авиационный технический университет»
ДИСКРЕТНАЯ МАТЕМАТИКА
Допущено Редакционно-издательским советом УГАТУ
в качестве учебного пособия для студентов
очной формы обучения, обучающихся
по направлению подготовки бакалавров
09.03.01 «Информатика и вычислительная техника»
и специальности
11.05.04 «Инфокоммуникационные технологии и системы специальной связи»
Уфа 2019
Авторы: С. С. Поречный, Н. И. Житникова,
Н. М. Шерыхалина, А. Р. Ураков
УДК 519.6(07)
ББК 22.19я7
Д67
Рецензенты:
зав. кафедрой математического моделирования БашГУ,
д-р физ.-мат. наук, проф. С. И. Спивак;
зав. кафедрой прикладной информатики БГПУ,
д-р техн. наук, проф. А. С. Филиппова
Д67 Дискретная математика : учеб. пособие / [С. С. Поречный и др.] ;
Уфимск. гос. авиац. техн. ун-т. – Уфа : РИК УГАТУ, 2019. – 391 с.
ISBN 978-5-4221-0764-3
Описаны базовые понятия теории множеств, теории графов и булевой алгебры. В главе, посвященной теории графов, помимо известных, представлены авторские алгоритмы нахождения метрических характеристик графов, а также аппроксимации нагруженного графа большой размерности графом меньшей размерности. В пособие включены практические задания и задания в тестовой форме по каждому из представленных разделов.
|
|
|
Предназначено для студентов, изучающих дискретную математику, математическую логику.
УДК 519.6(07)
ББК 22.19я7
ISBN 978-5-4221-0764-3 © Корректура и верстка. РИК УГАТУ, 2019
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ................................................................................................ 4
1. ТЕОРИЯ МНОЖЕСТВ.......................................................................... 6
1.1. Понятие множества....................................................................... 6
1.2. Операции над множествами....................................................... 14
1.3. Отношения и функции................................................................ 18
1.4. Специальные бинарные отношения.......................................... 23
1.5. Мощность множества................................................................. 28
1.6. Элементы комбинаторики.......................................................... 32
1.7. Практические задания................................................................. 38
1.8. Задания в тестовой форме........................................................... 49
2. ТЕОРИЯ ГРАФОВ............................................................................... 79
2.1. Общие понятия теории графов................................................... 79
2.2. Маршруты и пути......................................................................... 85
2.3. Матрицы смежности и инцидентности...................................... 88
|
|
|
2.4. Связность. Компоненты связности............................................ 90
2.5. Расстояния, нагруженный граф, деревья................................... 96
2.6. Планарность, раскраска графов. Сети и потоки..................... 107
2.7. Некоторые алгоритмы теории графов..................................... 120
2.8. Практические задания по алгоритмам..................................... 218
2.9. Практические задания............................................................... 248
2.10. Задания в тестовой форме....................................................... 251
3. АЛГЕБРА ЛОГИКИ........................................................................... 311
3.1. Основные определения............................................................... 311
3.2. Представление булевых функций............................................. 319
3.3. Полнота и замкнутость............................................................... 323
3.4. Практические задания............................................................... 338
3.5. Задания в тестовой форме......................................................... 345
ЗАКЛЮЧЕНИЕ...................................................................................... 375
СПИСОК ЛИТЕРАТУРЫ..................................................................... 376
ПРИЛОЖЕНИЕ .................................................................................... 377
ВВЕДЕНИЕ
Дискретная математика занимается изучением конечных свойств объектов, возникающих как в различных разделах математики, так и в ее технических приложениях. Под конечными свойствами понимаются их ограниченность или перечислимость.
|
|
|
Важными отличиями разделов дискретной математики от классических разделов непрерывной математики являются отсутствие понятия непрерывности и предела последовательности. В разделах дискретной математики рассматриваются конечные свойства объектов, но встречаются и бесконечные совокупности объектов или их конфигураций, однако, чаще всего эти бесконечности являются счетными. В то время как в непрерывной математике бесконечности, как правило, континуальные.
Разделы дискретной математики всегда существовали в математике, но стали выделяться в самостоятельную дисциплину в связи с развитием средств связи и появлением компьютеров. К разделам дискретной математики обычно относят: математическую логику, теорию алгоритмов, булеву алгебру, теорию конечных автоматов, теорию дискретных групп, теорию графов, комбинаторику, теорию чисел и много других разделов. Характерными примерами приложений различных разделов дискретной математики являются: методы распознавания образов, основанные на теории принятия решений, криптографические протоколы, теория кодирования информации, теория сложности алгоритмов и т. д.
|
|
|
Курс дискретной математики, входящий в программу для ряда направлений УГАТУ, состоит из: теории множеств (включая комбинаторику), теории графов, функций алгебры логики, автоматных функций, теории кодирования, синтеза схем из функциональных элементов и алгебры высказываний.
Данное пособие состоит из трех разделов. В первом разделе излагаются элементы теории множеств и комбинаторики, причем в таком объеме, который позволяет обеспечить приемлемую строгость изложения в последующих разделах, например, при оценке мощностей замкнутых классов.
Во втором разделе приводятся базовые понятия теории графов. Основные положения иллюстрируются примерами прикладного характера. Разбирается ряд алгоритмов поиска минимальных расстояний, компонент связности и других задач. Раздел содержит авторские алгоритмы нахождения метрических характеристик графов, а также аппроксимации нагруженного графа большой размерности графом меньшей размерности.
В третьем разделе рассматриваются основные положения алгебры логики. Здесь особую роль играет множество {0, 1}, элементы которого не являются числами в обычном смысле, хотя по некоторым свойствам и похожи на них. Рассматривается понятие полноты систем булевых функций, критерий и примеры, а также правила и способы определения мощностей множеств, составленных из специальных классов булевых функций.
Каждый раздел пособия содержит теоретический материал, сопровождаемый достаточным числом примеров, и завершается практическими задачами для самостоятельного решения. Причем количество задач таково, что пособие может быть использовано преподавателями на практических занятиях. Помимо задач каждый раздел пособия содержит 30 вариантов тестов (каждый тест состоит из 10 заданий), которые могут использоваться для проведения рубежного контроля.
Учебное пособие написано по материалам лекций и практических занятий по курсу дискретной математики, которые проводят авторы.
1. теориЯ множеств
1.1. Понятие множества
Некоторые понятия теории множеств были сформулированы в школьном курсе математики. В рамках данного раздела дискретной математики проводится обоснование и формализация этих понятий. Кроме того, вводятся новые понятия и свойства, которые могут казаться на первый взгляд неочевидными, а иногда и парадоксальными.
Теория множеств – учение об общих свойствах множеств, это фундаментальный математический аппарат, являющийся основой для всех разделов математики. Понятие множества в равной степени относится как к дискретной, так и к классической непрерывной математике. Впрочем, само разделение математики весьма условно.
Универсальность языка теории множеств позволяет применять её в математическом анализе, теории вероятностей и других областях математики. Общие свойства абстрактных отношений проявляются в матричной алгебре, операторном исчислении и т. д. Теория множеств позволила сформулировать понятие изоморфизма систем объектов, заданных вместе со связывающими их отношениями.
С множествами, как таковыми, математика оперирует с начала своего существования. Однако формирование понятия «множество» начало происходить значительно позже – в 19 в. Большое влияние на формирование этого понятия оказали работы Больцано, Дедекинда, Дюбуа-Реймона, но эти математики рассматривали лишь конечные множества.
Переход к изучению бесконечных множеств и операций над ними представлял принципиальную трудность. Свидетельством последнего являются различные противоречия (антиномии теории множеств), открытые разными учеными к 1900 г. Изучение бесконечных множеств было начато в работах Георга Кантора в 1871–1883 гг., которые встречали активное сопротивление современников. Кантор употреблял вначале термин Inbegrift – «совокупность», затем Mannigfaltigkeit – «многообразие», и наконец, Menge – «множество», в настоящее время сохранилось его обозначение множества M = {m}, которое он ввел в 1895 г.
Официальное признание теории множеств прозвучало на Первом международном математическом конгрессе (Цюрих, 1897 г.), где Адамар и Гурвиц указали на важные применения этой теории к анализу. Большое значение в распространении идей теории множеств принадлежит Гильберту. Именно он сказал: «Никто не сможет нас изгнать из рая, созданного Кантором».
Георг Кантор считается основателем современной теории множеств. В его работах началось построение аксиоматической теории множеств, хотя первая система аксиом теории множеств была предложена позднее в работах Цермело в 1904–1908 гг. Эта система аксиом позволила получить важные для математики результаты по теории множеств. Но лишь в 1940 году Гедель построил наиболее полную систему аксиом и доказал ее непротиворечивость.
Понятие множества с современной точки зрения считается интуитивно заданным. Попытки дать определение множества приводят к сведению понятия множества к другим подобного рода понятиям: совокупность, набор и т. д.
Что же такое множество по Г. Кантору? Множество по Кантору – это любое собрание определенных и различных между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое.
Таким образом, каждое множество состоит из объектов, которые в дальнейшем называются элементами множества. Множества обычно обозначаются большими буквами: А, Х и т. д. Элементы же множеств, как правило, обозначают маленькими буквами: а, х и т. д. Для записи того, что а является элементом множества А применяется значок Î (символ принадлежности). Пишут: аÎА и говорят, что элемент а принадлежит множеству А. В случае, когда а не является элементом множества А, пишут аÏА. Множество может содержать как конечное, так и бесконечное число элементов, соответственно, говорят, что множество конечно или бесконечно. Существенной деталью является то, что для любого рассматриваемого объекта можно установить, принадлежит он множеству или нет (третьего варианта не может быть).
Помимо этого будем применять следующие обозначения:
ü Æ – пустое множество, т. е. множество, не имеющее ни одного элемента (наличие такого множества предполагается второй аксиомой Геделя);
ü N – множество натуральных чисел;
ü Z – множество целых чисел;
ü Q – множество рациональных чисел;
ü R – множество действительных чисел.
Добавление к множествам Z, Q, R знака «+» выделяет из них только положительные числа, например, R+ – множество действительных положительных чисел.
ü 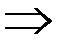 - если …, то…;
- если …, то…;
ü 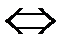 - … тогда и только тогда, когда…;
- … тогда и только тогда, когда…;
ü  … - для любых, для каждого…;
… - для любых, для каждого…;
ü  - существует, существуют;
- существует, существуют;  – существует единственный;
– существует единственный;
ü 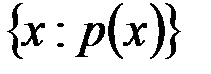 - множество таких элементов x, для которых выполняется условие
- множество таких элементов x, для которых выполняется условие 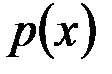 ;
;
ü 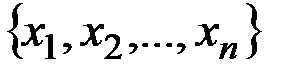 - множество, состоящее из элементов x1, x2, …,xn;
- множество, состоящее из элементов x1, x2, …,xn;
ü 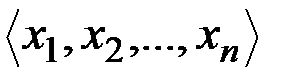 - упорядоченный набор элементов x1, x2, …, xn.
- упорядоченный набор элементов x1, x2, …, xn.
Множество задают двумя способами:
1) перечислением элементов;
2) характеристикой свойств, общих для элементов множества:
А = {x: P(x)} (А – множество тех и только тех элементов x, которые удовлетворяют условию P(x)).
Примеры
v А = {1, 2, 3, 4, 5, 6, 7, 8};
v А = {x: x ÎZ, 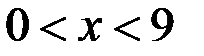 }, т. е. А - есть множество всех x, таких, что x - целое и x > 0 и x < 9.
}, т. е. А - есть множество всех x, таких, что x - целое и x > 0 и x < 9.
Интуитивный принцип объемности Г. Кантора (1 аксиома Геделя): множества А и В считаются равными (А = В), если они состоят из одних и тех же элементов.
Неравные множества А и В обозначаются так: 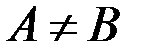 .
.
Примеры
v {1,2,3} = {2,1,3} = {2,3,1}.
v {{1,2}} 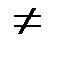 {1,2}, т. е. элемент не считается равным множеству, если даже множество состоит только из этого элемента (элементы множества окружены некоей воображаемой оболочкой, объединяющей их; при включении множества в другое множество оболочка сохраняется).
{1,2}, т. е. элемент не считается равным множеству, если даже множество состоит только из этого элемента (элементы множества окружены некоей воображаемой оболочкой, объединяющей их; при включении множества в другое множество оболочка сохраняется).
v А = {множество всех положительных четных целых чисел},
В = {множество всех положительных целых чисел, представимых в виде суммы двух положительных нечетных целых чисел}. Очевидно, что А = В.
Символом « 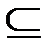 » обозначается отношение включения множеств, т. е.
» обозначается отношение включения множеств, т. е. 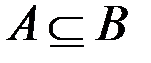 означает, что каждый элемент множества А является элементом множества B. В этом случае A называется подмножеством множества B, а B – надмножеством A. Если
означает, что каждый элемент множества А является элементом множества B. В этом случае A называется подмножеством множества B, а B – надмножеством A. Если 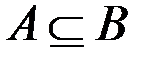 и
и 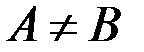 , то A называется собственным подмножеством B, и в этом случае записывается
, то A называется собственным подмножеством B, и в этом случае записывается 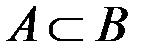 .
.
Примеры
v {1,2}Ì{1,2,3,4};
v Множество A = {x: xÎZ, x = 2n, nÎZ} четных чисел есть собственное подмножество множества Z целых чисел.
Свойства отношения включения:
1) ХÍХ (свойство рефлексивности);
2) если XÍY, YÍZ, то XÍZ (свойство транзитивности);
3) если XÍY, YÍX, то X = Y (свойство антисимметрии, см. подглаву 1.4);
4) для любого множества X справедливо ÆÍX, т. е. пустое множество есть подмножество любого множества.
Доказательство
Докажем последнее свойство от противного. Пусть Æ не включено в множество X. Это означает, что должно существовать хÎÆ такое, что хÏX. Но для любого х справедливо хÏÆ. Следовательно, такого х не существует и ÆÍ X.
? Замечание. Необходимо четко различать отношения Ì и Î. Справедливо: 1Î{1,2}, {1}Ì{1,2}, {1}Î{{1}}, {1}Í{1} (однако, 1Ï{{1}}, так как единственным элементом {{1}} является {1}).
& Определение . Множество всех подмножеств множества A называют множеством-степенью или Булеаном, и обозначается B(A).
Пример
v Если А = {1,2,3}, то B(А) = {Æ,{1},{2},{3},{1,2},{1,3},{2,3}, А}.
& Утверждение. Если A состоит из n элементов, то B(A) состоит из 2n элементов.
Доказательство . Перенумеруем все элементы множества А от 1 до n. Введем описание подмножества множества А в виде строки из n ячеек, содержащих цифры 0 или 1. 0 на i-м месте означает, что
i-й элемент не принадлежит данному подмножеству, 1 – что принадлежит:
| 0 | 1 | 0 | 0 | … | 1 | 0 | 1 |
Например, пустое множество обозначается строкой нулей, само А – строкой единиц.
Тогда число различных комбинаций нулей и единиц равно количеству различных двоичных чисел, которые можно записать в n ячейках, т. е. 2n.
& Определение . Универсальное множество (универсум) U – множество всех множеств или множество, содержащее все возможные элементы.
В каждом конкретном случае под U можно понимать множество всех элементов, подлежащих рассмотрению (множество всех людей, множество всех сотрудников данного учреждения, множество всех действительных чисел и т. д.).
Интуитивный принцип абстракции Г. Кантора: любая форма Р(х) определяет некоторое множество А посредством условия, согласно которому элементами множества А являются в точности такие объекты а, что Р(а) есть истинное высказывание.
Оказалось, что интуитивный принцип абстракции не совсем точен и может привести к парадоксам. Один из таких парадоксов был приведен в 1902 г. Б. Расселом.
Парадокс Рассела
Будем говорить, что множество А обладает свойством D, если для него верно АÏА. Введем теперь множество
Т = {А: А удовлетворяет свойству D}.
Заметим, что если ТÎТ, то множество Т не удовлетворяет свойству D и, следовательно, ТÏТ. Если же ТÏТ, то множество Т удовлетворяет свойству D и, следовательно, ТÎТ.
Приведем еще одну интерпретацию парадокса Рассела. Условимся называть множество «обычным», если оно не является своим собственным элементом. Например, множество всех людей является «обычным», так как само множество – не человек. Примером «необычного» множества является множество всех множеств, так как оно само является множеством, а, следовательно, само является собственным элементом.
Можно рассмотреть множество, состоящее только из всех «обычных» множеств, такое множество называется расселовским множеством. Парадокс возникает при попытке определить, является ли это множество «обычным» или нет, т. е. содержит ли оно себя в качестве элемента. Есть две возможности: 1) с одной стороны, если оно «обычное», то оно должно включать себя в качестве элемента, так как оно по определению состоит из всех «обычных» множеств. Но тогда оно не может быть «обычным», так как «обычные» множества – это те, которые себя не включают. 2) Остается предположить, что это множество «необычное». Однако оно не может включать себя в качестве элемента, так как оно по определению должно состоять только из «обычных» множеств. Но если оно не включает себя в качестве элемента, то это «обычное» множество.
Другая интерпретация парадокса: в одном полку жил-был полковой парикмахер, которого называли брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел, а потом сел на пенек и задумался: а что ему с собой-то делать? Ведь если он будет брить себя, то нарушит приказ командира не брить тех, кто бреется сам. Брадобрей уже решил было, что брить себя не будет. Но тут его осенила мысль, что если он сам себя брить не будет, то окажется, что он сам не бреется, и по приказу командира он должен все-таки себя побрить...
Уточнением интуитивного принципа абстракции является аксиома выбора Геделя, позволяющая избежать указанного парадокса: для любого высказывания Р и любого множества А существует множество, состоящее из тех и только тех элементов множества А, для которых высказывание Р(х) является истинным, то есть форма задается в виде {xÎA: P(x)}.
Семейства множеств
Пусть U – универсальное множество. Если каждому натуральному числу n взаимно однозначно сопоставлено некоторое подмножество An 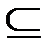 U, то тем самым определена последовательность множеств A1,…,An,… или, в короткой записи, (An)nÎN. Предположим теперь, что вместо множества N натуральных чисел задано произвольное множество I и каждому элементу iÎI взаимно однозначно сопоставлено подмножество Ai
U, то тем самым определена последовательность множеств A1,…,An,… или, в короткой записи, (An)nÎN. Предположим теперь, что вместо множества N натуральных чисел задано произвольное множество I и каждому элементу iÎI взаимно однозначно сопоставлено подмножество Ai 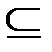 U. Тогда говорят, что задано (индексированное) семейство множеств (Ai)iÎI.
U. Тогда говорят, что задано (индексированное) семейство множеств (Ai)iÎI.
Множество I называют множеством индексов, а множества Ai – элементами семейства (Ai)iÎI. В случае I 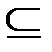 N получаем последовательность множеств, или счетное семейство множеств; если множество I конечно, получаем конечное семейство множеств. Таким образом, семейство (Ai)iÎI определено, если задано отображение
N получаем последовательность множеств, или счетное семейство множеств; если множество I конечно, получаем конечное семейство множеств. Таким образом, семейство (Ai)iÎI определено, если задано отображение
ν: I→2U. Отметим, что любое множество, элементы которого есть некоторые подмножества универсального множества U, т. е. любое множество A 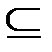 2U, можно считать семейством (Ai)iÎI, где I = A, a ν – тождественное отображение множества A на себя.
2U, можно считать семейством (Ai)iÎI, где I = A, a ν – тождественное отображение множества A на себя.
Пример
v Рассмотрим в качестве множества индексов множество точек некоторой гладкой плоской кривой и каждой точке сопоставим касательную, проведенную к кривой в этой точке (которая будет единственной в силу гладкости). Тогда получаем семейство множеств, элементами которого служат множества точек различных касательных (рис. 1.1).
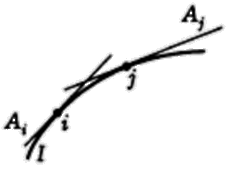
Рис. 1.1 Пример семейства множеств
Аксиомы теории множеств
Ниже приводится перечень аксиом теории множеств, которые использовались различными математиками для построения аксиоматической теории множеств. Этот перечень не является полным, в него включены аксиомы, посвященные основам теории множеств. Существует ряд аксиом, связанных с более глубокими понятиями в теории множеств. Перечисленные ниже аксиомы нельзя рассматривать и как единый набор, так как в совокупности они являются зависимыми.
1. Аксиома объемности. Если множества А и В составлены из одних и тех же элементов, то они совпадают.
2. Аксиома существования пустого множества. Существует такое множество Æ, что ни один элемент х ему не принадлежит.
3. Аксиома пары. Для произвольных а и b существует множество, единственными элементами которого являются а и b.
4. Аксиома суммы. Для каждого семейства множеств А существует множество S, состоящее из тех и только тех элементов, которые принадлежат некоторому множеству Х, принадлежащему А.
5. Аксиома степени. Для каждого множества А существует семейство множеств Р, элементами которого являются все подмножества множества А и только они.
6. Аксиома бесконечности. Существует такое семейство множеств А, которому принадлежит Æ и если, ХÎА, то в А найдется элемент Y, состоящий из всех элементов множества Х и самого множества Х.
7. Аксиома выбора. Для каждого семейства А непустых непересекающихся множеств существует множество В, имеющее один и только один общий элемент с каждым из множеств Х, принадлежащих А.
8. Аксиома выделения для высказывательной функции Ф. Для произвольного множества А существует множество, состоящее из тех и только тех элементов множества А, которые (будучи подставлены на место переменных х) удовлетворяют Ф.
9. Аксиома замены для высказывательной функции Ф. Если для каждого х существует единственный элемент у, такой что выполняется Ф(х, у), то для каждого множества А существует множество В, состоящее из тех и только тех элементов у, которые при некотором хÎА выполняют Ф(х, у).
10. Аксиома регулярности. Для любого непустого семейства множеств А существует такое множество Х, что ХÎА и ХÇА = Æ.
В систему аксиом Цермело (первую предложенную систему аксиом) входили аксиомы 1, 5, 6, 7, 8. В системе Цермело–Френкеля аксиома 8 была заменена на аксиому 9. В настоящее время системы аксиом различаются по типам: наиболее известными считаются системы Цермело–Френкеля и Геделя–Бернайса. Обычно в систему аксиом Цермело–Френкеля включают аксиомы 1–6, 9.
1.2. Операции над множествами
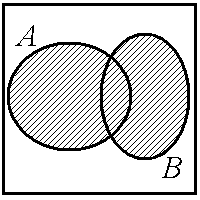
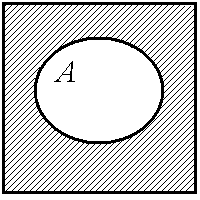
Операции над множествами хорошо иллюстрируют диаграммы Эйлера–Венна (см. рис. 1.2). При этом универсум U обозначается квадратом, остальные множества обозначаются геометрическими фигурами (кругами, овалами, треугольниками, прямоугольниками) внутри этого квадрата.
& Определение. Объединением множеств А и В называется множество всех элементов, которые являются элементами множества А или элементами множества В:
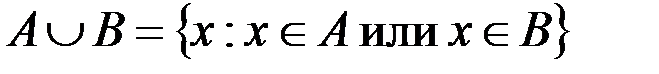 .
.
Некоторые свойства операции объединения:
ü 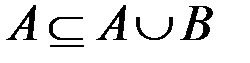 ;
;
ü 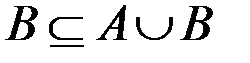 .
.
На диаграмме (рис. 1.2, а) заштриховано множество  .
.
& Определение. Пересечением множеств А и В называется множество всех элементов, которые одновременно являются и элементами множества А, и элементами множества В:
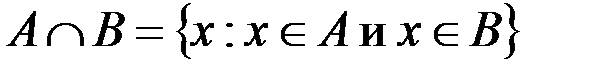 .
.
Некоторые очевидные свойства операции пересечения:
ü 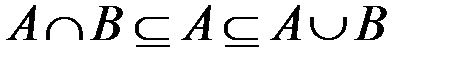 ;
;
ü 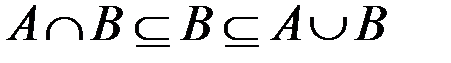 .
.
На диаграмме (рис. 1.2, б) заштриховано множество  .
.
& Определение. Отрицанием (или абсолютным дополнением) множества А называется множество всех элементов, не принадлежащих множеству А: 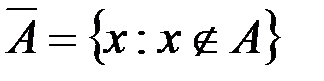 .
.
На диаграмме (рис. 1.2, в) заштриховано множество 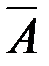 .
.
| 
| 
|
| а | б | в |
Рис. 1.2. Операции над множествами:
а – объединение множеств А и В: 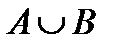 ; б – пересечение множеств А и В:
; б – пересечение множеств А и В: 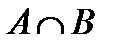 ;
;
в – абсолютное дополнение множества А: 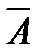
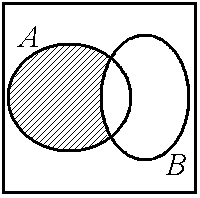
& Определение. Разностью множества А и множества В (или относительным дополнением множества B до множества А)называется множество элементов, принадлежащих множеству А и одновременно не принадлежащих множеству B:
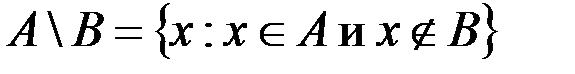 .
.
На диаграмме (рис. 1.3, а) заштриховано множество 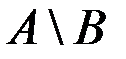 .
.
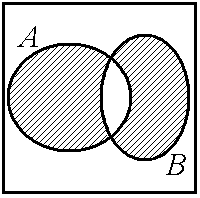
& Определение. Симметрической разностью множеств А и В называется объединение относительных дополнений множества А до В и множества В до А: 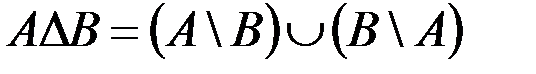 .
.
На диаграмме (рис. 1.3, б) заштриховано множество 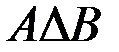 .
.
| 
|
| а | б |
Рис. 1.3. Операции над множествами:
а – разность множества А и множества В: 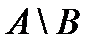 ;
;
б – симметрическая разность множеств А и В: 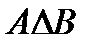
Свойства действий над множествами
| 1. | 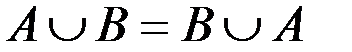
| 1¢. | 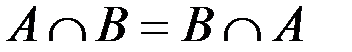
|
| 2. | 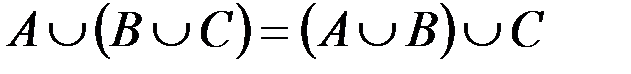
| 2¢. | 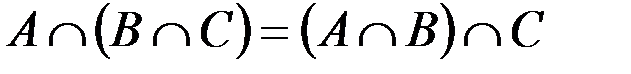
|
| 3. | 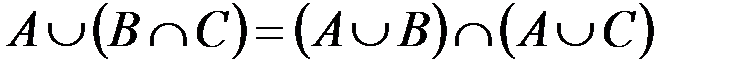
| 3¢. | 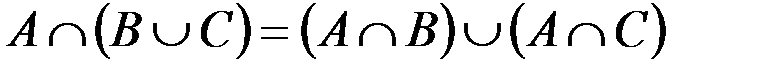
|
| 4. | 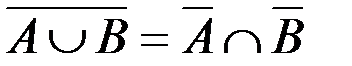
| 4¢. | 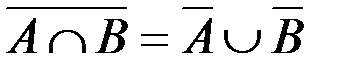
|
| 5. | 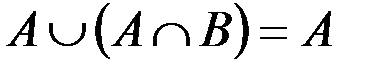
| 5¢. | 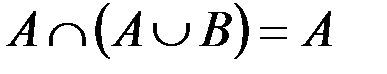
|
| 6. | AÈÆ = A | 6¢. | AÇÆ = Æ |
| 7. | AÈ 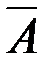 = U = U
| 7¢. | AÇ 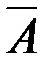 = Æ = Æ
|
| 8. | AÈA = A | 8¢. | AÇA = A |
| 9. | AÈU = U | 9¢. | AÇU = A |
| 10. | AÈB = B, если 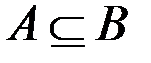
| 10¢. | AÇB = A, если 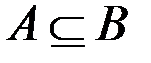
|
Некоторые из приведенных свойств имеют специальные названия: 1 и 1¢ – свойства коммутативности, 2 и 2¢ – ассоциативности, 3 и 3¢ – дистрибутивности, 4 и 4¢ – законы де Моргана, 5 и 5¢ – законы поглощения, 8 и 8¢ – законы идемпотентности.
Докажем свойство дистрибутивности объединения относительно пересечения (свойство 3): 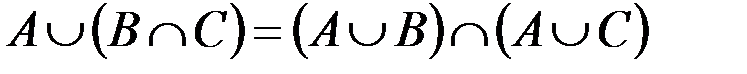 .
.
Доказательство. Будем использовать свойство отношения включения множеств: два множества равны, если являются подмножествами друг друга. Таким образом, нужно показать, что множество 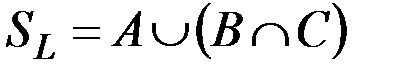 , описанное в левой части равенства, является подмножеством множества
, описанное в левой части равенства, является подмножеством множества 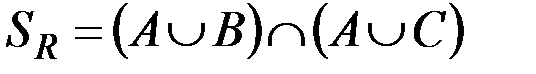 , описанного в правой части, и одновременно
, описанного в правой части, и одновременно 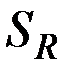 является подмножеством
является подмножеством 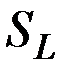 .
.
Докажем сначала вложение 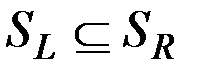 . Для этого возьмем произвольный элемент
. Для этого возьмем произвольный элемент 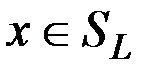 , т. е.
, т. е. 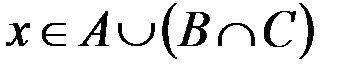 . По определению операций объединения и пересечения множеств, это означает, что или
. По определению операций объединения и пересечения множеств, это означает, что или 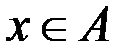 , или
, или 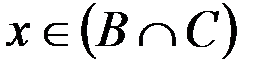 . Это записывается так:
. Это записывается так: 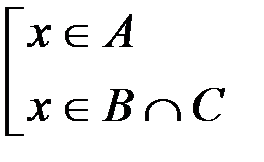 . В свою очередь, последнее утверждение равносильно следующему:
. В свою очередь, последнее утверждение равносильно следующему: 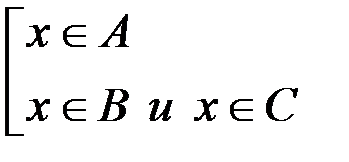 . Это можно записать так:
. Это можно записать так: 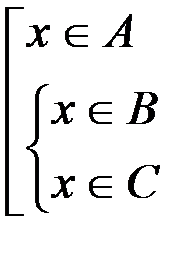 . Последнее утверждение можно трактовать так:
. Последнее утверждение можно трактовать так: 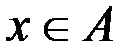 или
или 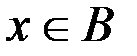 и одновременно
и одновременно 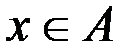 или
или 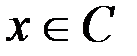 , т. е.
, т. е. 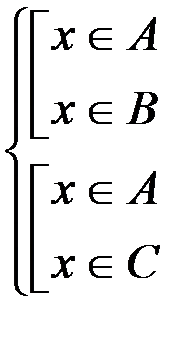 . Это в свою очередь означает, что
. Это в свою очередь означает, что 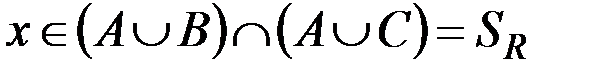 . Таким образом, любой элемент множества
. Таким образом, любой элемент множества 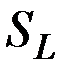 является элементом множества
является элементом множества 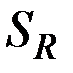 , что доказывает вложение
, что доказывает вложение 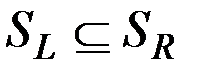 .
.
Докажем теперь вложение 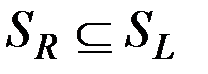 . Пусть теперь
. Пусть теперь 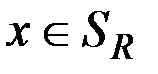 , т. е.
, т. е. 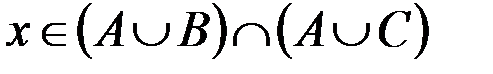 , что по определению равносильно
, что по определению равносильно 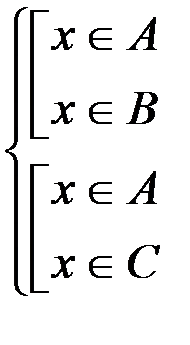 . Здесь возможны два варианта: либо
. Здесь возможны два варианта: либо 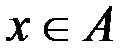 (это условие есть во всех предлагающихся наборах «или»), либо
(это условие есть во всех предлагающихся наборах «или»), либо 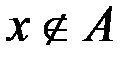 . Во втором случае элемент x обязан принадлежать множеству B (из первой скобки «или») и множеству C (из второй скобки «или»), т. е.
. Во втором случае элемент x обязан принадлежать множеству B (из первой скобки «или») и множеству C (из второй скобки «или»), т. е. 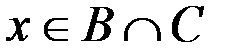 . Следовательно,
. Следовательно, 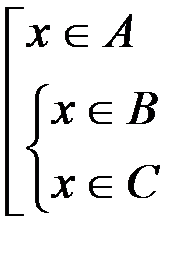 , что означает принадлежность элемента x левой части равенства
, что означает принадлежность элемента x левой части равенства 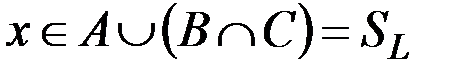 . Значит,
. Значит, 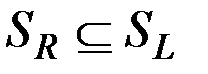 .
.
Из доказанных вложений 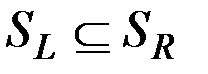 и
и 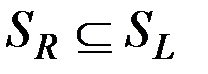 делается вывод о равенстве
делается вывод о равенстве 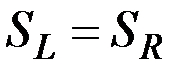 или
или 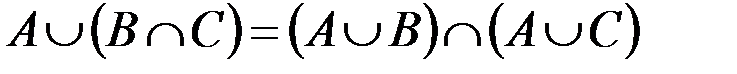 , что и требовалось доказать.
, что и требовалось доказать.
? Замечание. Часто объединение множеств называют суммой множеств. Однако, в отличие от обычной «суммы» элементов, общие элементы в объединение множеств входят один раз.
Пример
v Если 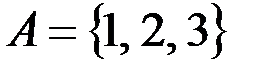 ,
, 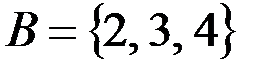 , то
, то 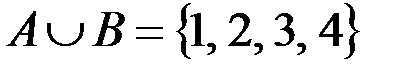 . Поэтому
. Поэтому 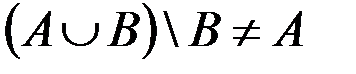 , в данном случае
, в данном случае 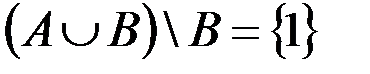 .
.
На законах де Моргана основан принцип двойственности, играющий важную роль в теории множеств и ее приложениях.
Принцип двойственности
Если в некотором равенстве, связывающем подмножества данного универсума, заменить все множества на их отрицания, универсальное множество заменить пустым, пустое - универсальным, операции объединения заменить на операции пересечения и наоборот, пересечение заменить объединением, то получится верное равенство. Полученное новое равенство называется двойственным по отношению к исходному.
1.3. Отношения и функции
& Определение. Упорядоченным набором длины n (обозначается 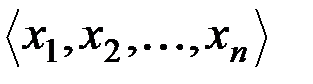 ) называется последовательность, состоящая из n элементов x1, x2, x3,…, xn некоторого множества, расположенных в определенном порядке.
) называется последовательность, состоящая из n элементов x1, x2, x3,…, xn некоторого множества, расположенных в определенном порядке.
В частности, упорядоченной парой 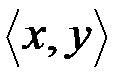 называется совокупность, состоящая из двух элементов x и y некоторого множества, расположенных в определенном порядке.
называется совокупность, состоящая из двух элементов x и y некоторого множества, расположенных в определенном порядке.
& Определение.Два набора длины n 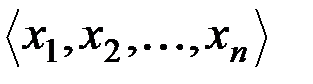 и
и 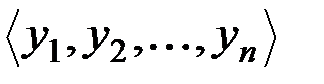 считаются равными тогда и только тогда, когда
считаются равными тогда и только тогда, когда 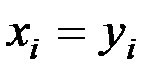 ,
, 
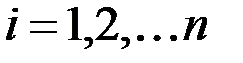 .
.
В частности, две пары 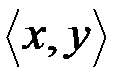 и
и 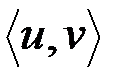 считаются равными тогда и только тогда, когда
считаются равными тогда и только тогда, когда 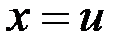 и
и 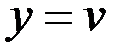 .
.
& Определение. Прямым произведением (декартовым произведением) множеств A1, A2,…, An называется множество упорядоченных наборов:
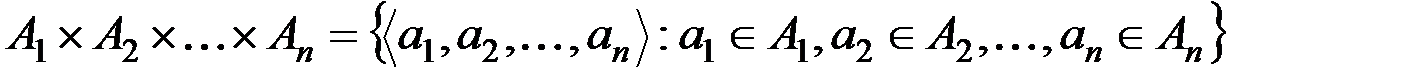 .
.
Если A1 = A2 = … = An = A, то множество 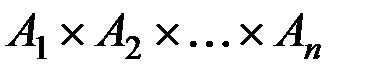 называется прямой степенью (или n -й декартовой степенью) множества A и обозначается через An.
называется прямой степенью (или n -й декартовой степенью) множества A и обозначается через An.
Примеры
v 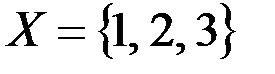 ,
, 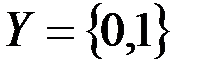 .
.
Тогда 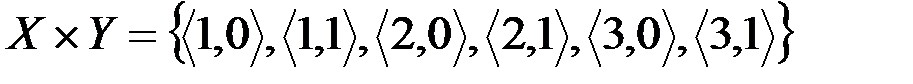 ,
,
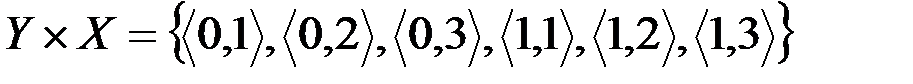 .
.
Заметим, что 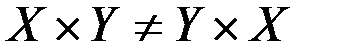 , если
, если 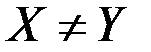 .
.
v Пусть 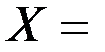 R,
R, 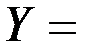 R, тогда
R, тогда 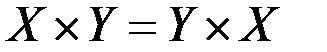 = R´R = R2 графически можно представить как множество точек плоскости
= R´R = R2 графически можно представить как множество точек плоскости 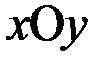 .
.
v Пусть 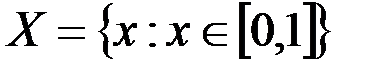 ,
, 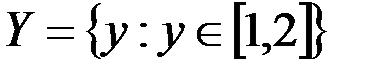 .
.
Тогда 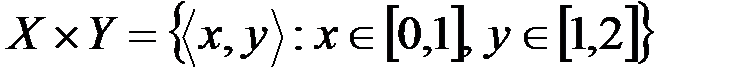 графически можно представить как множество точек квадрата (см. рис 1.4).
графически можно представить как множество точек квадрата (см. рис 1.4).
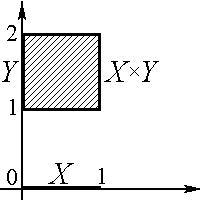
Рис. 1.4. Пример прямого произведения:
заштрихованная область − множество точек квадрата 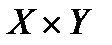 .
.
& Определение. Бинарным (двуместным) отношением между элементами множеств А и В называется любое подмножество 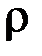 множества
множества 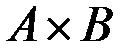 . Если А = В, отношение называется бинарным на А.
. Если А = В, отношение называется бинарным на А.
Записи 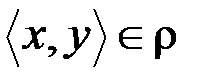 и
и 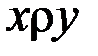 означают, что пара
означают, что пара 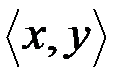 принадлежит бинарному отношению
принадлежит бинарному отношению 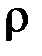 . Элементы x и y называют координатами или компонентами отношения
. Элементы x и y называют координатами или компонентами отношения 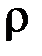 .
.
& Определение. Областью определения бинарного отношения 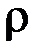 называют множество
называют множество
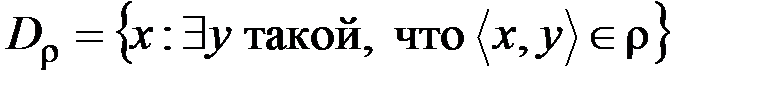 .
.
& Определение. Областью значений бинарного отношения 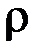 называют множество
называют множество
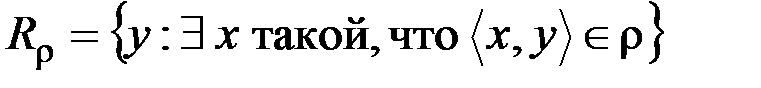 .
.
Примеры
v Множество 
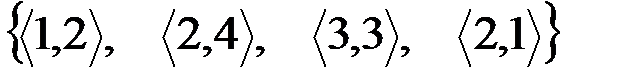 – бинарное отношение, Dr = {1,2,3}, Rr = {2,4,3,1} = {1,2,3,4}.
– бинарное отношение, Dr = {1,2,3}, Rr = {2,4,3,1} = {1,2,3,4}.
v Множество, задающее бинарное отношение равенства на множестве действительных чисел R (специальное обозначение « 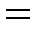 »):
»): 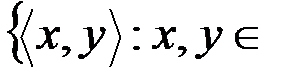 R
R 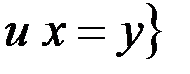 , Dr = R, Rr = R.
, Dr = R, Rr = R.
v Множество, задающее бинарное отношение «меньше чем» на множестве целых чисел Z (специальное обозначение « 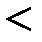 »):
»): 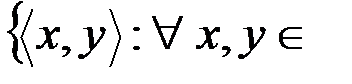 Z
Z 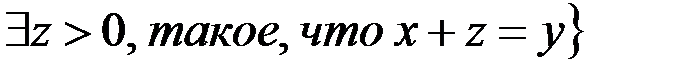 , Dr = Rr = Z. Аналогично можно построить множества, задающие отношения
, Dr = Rr = Z. Аналогично можно построить множества, задающие отношения
«  », «
», « 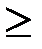 », «
», « 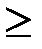 ».
».
Для бинарных отношений определены обычным образом теоретико-множественные операции объединения, пересечения и т. д.
Дополнением бинарного отношения r между элементами А и В считается множество 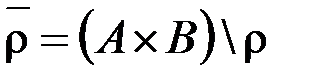 .
.
Пример
v Зададим на прямом произведении множеств  и
и 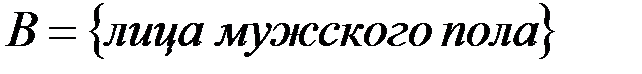 отношение
отношение 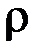 : «быть супругами». Тогда дополнением этого отношения будет множество всевозможных разнополых пар из
: «быть супругами». Тогда дополнением этого отношения будет множество всевозможных разнополых пар из 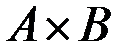 , не связанных брачными узами.
, не связанных брачными узами.
& Определение. Обратным отношением для бинарного отношения r называется отношение 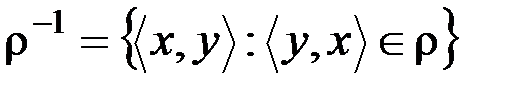 .
.
Примеры
v Числовую функцию можно рассмотреть как бинарное отношение, заданное на числовых множествах. В этом случае обратная функция будет играть роль обратного бинарного отношения.
v Зададим на множестве 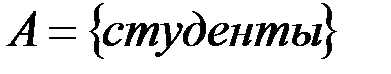 отношение
отношение 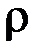 : «быть ниже ростом» или
: «быть ниже ростом» или 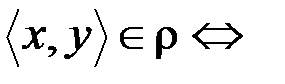 студент x ниже ростом, чем студент y. Обратным к
студент x ниже ростом, чем студент y. Обратным к 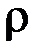 будет отношение
будет отношение 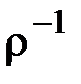 : «быть не ниже ростом».
: «быть не ниже ростом».
& Определение. Образом множества 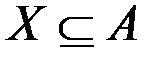 относительно
относительно 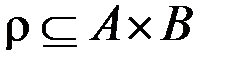 называется множество
называется множество
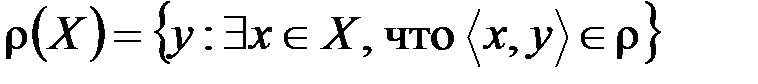 .
.
Прообразом 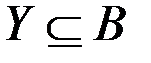 относительно r называется
относительно r называется 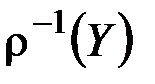 .
.
& Определение. Композицией отношений 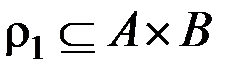 и
и 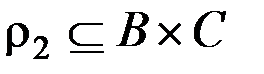 называется отношение на множестве
называется отношение на множестве 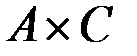 :
:
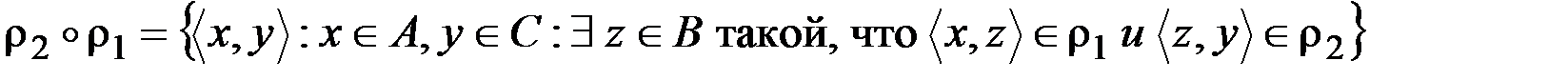 .
.
Пример
v 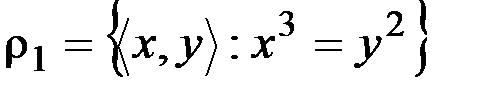 ,
, 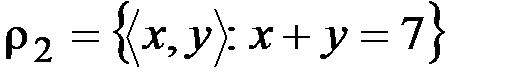 . Необходимо найти отношение, для которого будет существовать такой z, а потом показать равенство отношений (вложенность туда-обратно):
. Необходимо найти отношение, для которого будет существовать такой z, а потом показать равенство отношений (вложенность туда-обратно): 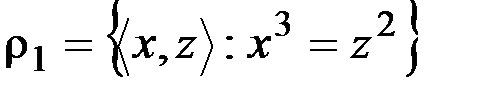 , так как
, так как 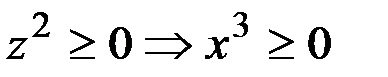 ,
, 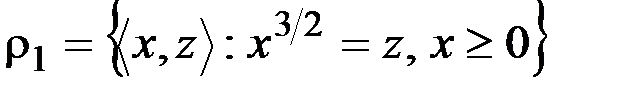 .
. 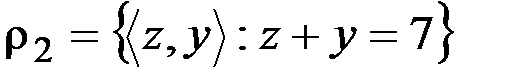 .
.
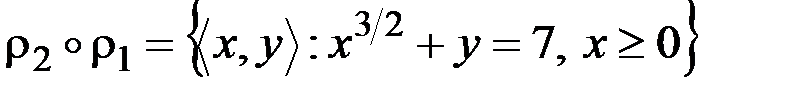 . Условие композиции будет выполняться:
. Условие композиции будет выполняться: 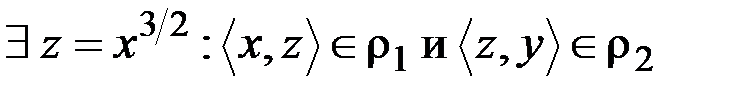 (для полного решения необходимо доказать равенство этих отношений).
(для полного решения необходимо доказать равенство этих отношений).
v 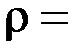 {<1,2>, <2,1>, <3,4>, <4,3>, <4,4>}.
{<1,2>, <2,1>, <3,4>, <4,3>, <4,4>}.
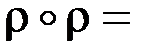 {<1,1>, <2,2>, <3,3>, <3,4>, <4,3>, <4,4>}.
{<1,1>, <2,2>, <3,3>, <3,4>, <4,3>, <4,4>}.
& Определение. Бинарное отношение f называется функцией из A в B (из A на B), если область определения отношения 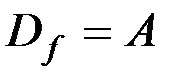 , область значений отношения
, область значений отношения 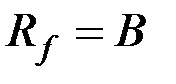 и для всех x, y1, y2 из условий
и для всех x, y1, y2 из условий 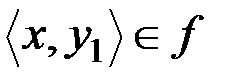 и
и 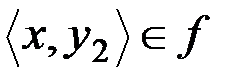 следует y1
следует y1 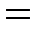 y2.
y2.
Если f – функция, то вместо 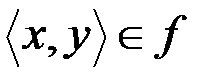 записывают
записывают 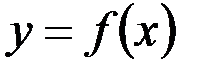 и y называют значением функции f при значении аргумента x или образом элемента x; x называют прообразом элемента y.
и y называют значением функции f при значении аргумента x или образом элемента x; x называют прообразом элемента y.
Функцию f из A в B (из A на B) также называют отображением множества A в множество B (на множество B) и обозначают 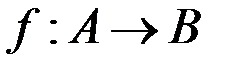 .
.
Примеры
v Множество пар 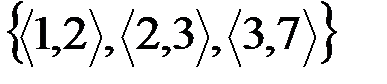 – функция.
– функция.
v Множество пар 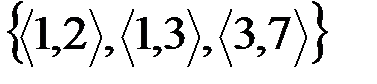 - не функция (1 отображается сразу на два элемента: 2 и 3).
- не функция (1 отображается сразу на два элемента: 2 и 3).
v 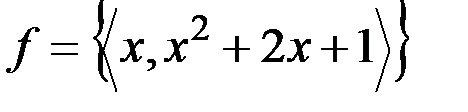 - функция
- функция 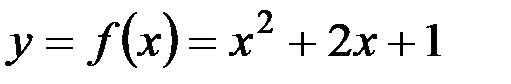 .
.
& Определение. Функция 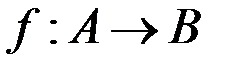 называется инъективной, если
называется инъективной, если 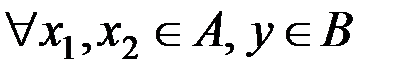 из того, что
из того, что 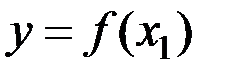 и
и 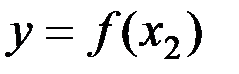 следует
следует 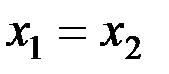 .
.
Таким образом, для инъективного отображения f одинаковые значения y могут соответствовать только одинаковым аргументам x.
Следует заметить, что функция, отображающая друг на друга линейно упорядоченные множества (в частности, числовая функция), может быть инъективной лишь в случае её строгой монотонности.
& Определение. Функция 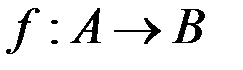 называется сюръективной, если
называется сюръективной, если 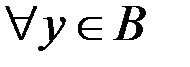 существует
существует 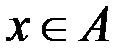 такой, что
такой, что 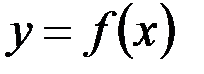 .
.
Это означает, что для сюръективного отображения каждому значению yÎB соответствует хотя бы одно значение x или 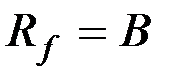 .
.
& Определение.Функция f называется биективной (или биекцией), если f одновременно сюръективна и инъективна. Говорят, что биективная функция f осуществляет взаимно однозначное соответствие между множествами A и B.
Примеры
Рассмотрим функции, осуществляющие отображение R 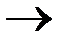 R:
R:
v 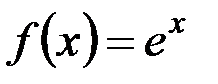 - инъективна (строго монотонна
- инъективна (строго монотонна 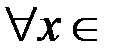 R), но не сюръективна (так как
R), но не сюръективна (так как 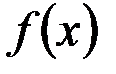 ни при каких значениях аргумента не принимает отрицательных значений и
ни при каких значениях аргумента не принимает отрицательных значений и 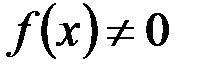 ).
).
v 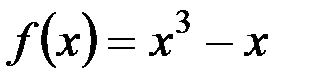 – сюръективна (принимает все возможные значения y
– сюръективна (принимает все возможные значения y 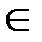 R), но не инъективна (поскольку
R), но не инъективна (поскольку 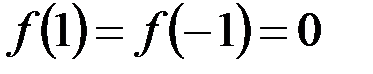 ).
).
v 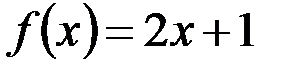 ,
, 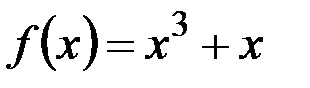 – биективные функции (всюду определенные и строго монотонные функции).
– биективные функции (всюду определенные и строго монотонные функции).
? Замечание. Отметим, что обратное отношение 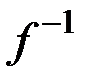 для функции f существует всегда. Для функциональности отношения
для функции f существует всегда. Для функциональности отношения 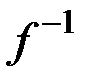 необходимо и достаточно, чтобы функция f являлась биекцией.
необходимо и достаточно, чтобы функция f являлась биекцией.
& Определение. n-местным отношением на множестве A называется любое подмножество множества An. Функцию 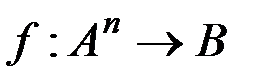 называют n -местной функцией (или функцией n переменных) из множества A в B и обозначают
называют n -местной функцией (или функцией n переменных) из множества A в B и обозначают 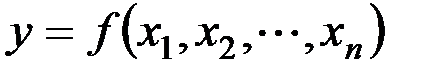 . При этом y называют значением функции f при значении аргументов x1,x2,…,xn.
. При этом y называют значением функции f при значении аргументов x1,x2,…,xn.
1.4. Специальные бинарные отношения
Специальные бинарные отношения задаются между элементами одного и того же множества A.
& Определение. Бинарное отношение r на множестве A называется рефлексивным, если 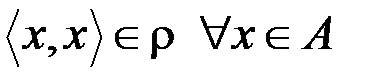 (каждый элемент множества находится в отношении с самим собой).
(каждый элемент множества находится в отношении с самим собой).
& Определение. Бинарное отношение r на множестве A называется антирефлексивным, если 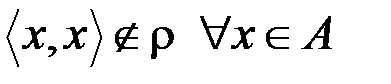 .
.
Следует различать свойства антирефлексивности и нерефлексивности (иррефлексивности): отношение r не рефлексивно, если найдется такой элемент  , что
, что 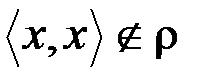 ; для антирефлексивного отношения это условие выполняется для всех
; для антирефлексивного отношения это условие выполняется для всех  .
.
Примеры
v Отношение « 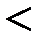 » на множестве R является антирефлексивным (не существует
» на множестве R является антирефлексивным (не существует 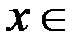 R:
R: 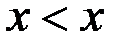 );
);
v Отношение 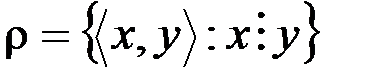 (
( 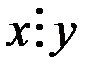 означает, что x делится на y без остатка) на множестве Z является не рефлексивным, так как существует элемент
означает, что x делится на y без остатка) на множестве Z является не рефлексивным, так как существует элемент 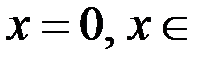 Z:
Z: 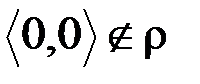 (на 0 делить нельзя). Очевидно, для всех остальных чисел из Z условие рефлексивности выполнено (число делится само на себя без остатка).
(на 0 делить нельзя). Очевидно, для всех остальных чисел из Z условие рефлексивности выполнено (число делится само на себя без остатка).
& Определение. Бинарное отношение r на множестве A называется симметричным, если 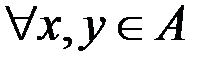 условие
условие 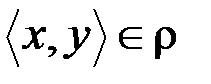 влечет
влечет 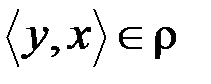 .
.
& Определение. Бинарное отношение r на множестве A называется антисимметричным, если 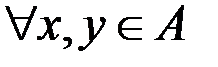 выполнение одновременно условий
выполнение одновременно условий 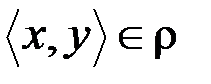 и
и 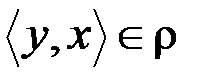 влечет равенство
влечет равенство 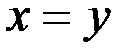 .
.
& Определение. Бинарное отношение r на множестве A называется строго антисимметричным, если 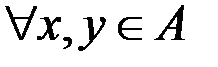 условие
условие 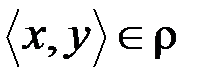 влечет
влечет 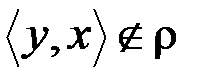 .
.
Следует различать свойства строгой антисимметричности и несимметричности отношения r: отношение r не симметрично, если найдутся такие элементы 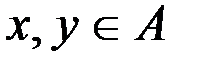 , что из
, что из 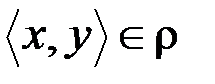 будет следовать
будет следовать 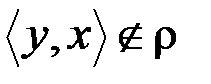 ; для строго антисимметричного отношения это условие выполняется для всех
; для строго антисимметричного отношения это условие выполняется для всех 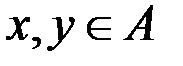 .
.
Примеры
v Отношение «  » на множестве R является строго антисимметричным.
» на множестве R является строго антисимметричным.
v Отношение 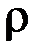 : «знать кого-либо» на множестве A людей является не симметричным: из того, что
: «знать кого-либо» на множестве A людей является не симметричным: из того, что 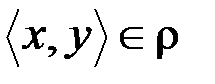 вовсе не следует
вовсе не следует 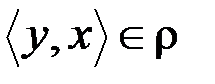 (если я знаю президента, то это не означает, что президент знает меня!) и если
(если я знаю президента, то это не означает, что президент знает меня!) и если 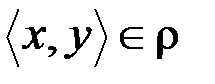 и
и 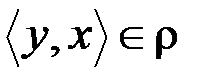 , тоэто не значит, что x = y (т. е. отношение не антисимметричное).
, тоэто не значит, что x = y (т. е. отношение не антисимметричное).
& Определение. Бинарное отношение r на множестве A называется транзитивным, если 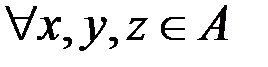 из условий
из условий 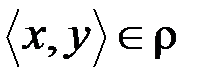 и
и 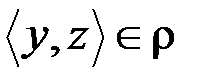 следует
следует 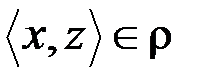 .
.
& Определение. Бинарное отношение r на множестве A называется антитранзитивным, если 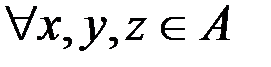 из условий
из условий 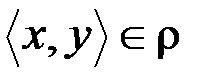 и
и 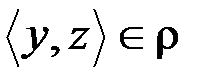 следует
следует 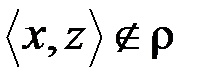 .
.
Бинарное отношение r на множестве A считается нетранзитивным, если 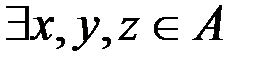 из условий
из условий 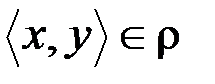 и
и 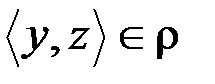 следует
следует 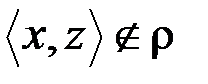 .
.
& Определение. Рефлексивное, симметричное и транзитивное отношение на множестве A называется отношением эквивалентности на множестве A (эквивалентностью на A).
Примеры
v Отношение равенства « 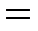 » на множестве целых (действительных) чисел – отношение эквивалентности.
» на множестве целых (действительных) чисел – отношение эквивалентности.
v Отношение геометрического подобия на множестве треугольников – отношение эквивалентности.
v Сравнимость по модулю 2 (или n) – отношение эквивалентности на множестве целых чисел.
v Отношение принадлежности к одной группе студентов – отношение эквивалентности на множестве всех студентов.
v Отношение «  » антирефлексивно, строго антисимметрично, транзитивно – не является отношением эквивалентности.
» антирефлексивно, строго антисимметрично, транзитивно – не является отношением эквивалентности.
Пусть задано отношение эквивалентности r на множестве А.
& Определение. Множество ХÍА называется классом эквивалентности для этого отношения, если оно удовлетворяет следующим условиям:
1) для любых хÎХ и уÎХ выполняется хrу;
2) если хÎХ , уÎА и хrу, то уÎХ.
Пусть на А задано отношение эквивалентности. Введем следующее обозначение: [x]r = {yÎA: хrу}. Нетрудно видеть из определений, что [x]r является классом эквивалентности. Его называют классом эквивалентности, порожденным элементом х.
Для классов эквивалентности [x]r и [y]r возможны только следующие 2 случая:
1) [x]r = [y]r;
2) [x]rÇ[y]r = Æ.
Примеры
v Отношение равенства: "xÎZ 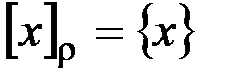 , т. е. каждый класс эквивалентности состоит из одного элемента – числа x.
, т. е. каждый класс эквивалентности состоит из одного элемента – числа x.
v Отношение сравнимости по модулю n: 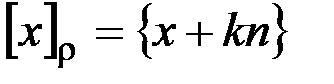 , "kÎZ.
, "kÎZ.
v Отношение принадлежности к одной группе студентов: класс эквивалентности – группа.
& Определение. Разбиением множества A называется совокупность попарно не пересекающихся подмножеств A, таких, что каждый элемент множества A принадлежит одному и только одному из этих подмножеств.
Примеры
v Пусть 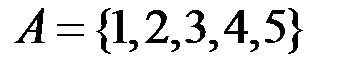 . Тогда одним из его разбиений можно считать следующее:
. Тогда одним из его разбиений можно считать следующее: 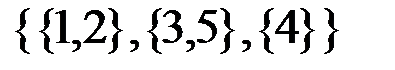 .
.
v Разбиением множества студентов университета может быть совокупность групп, в которых они обучаются.
Если {Aa} – некоторое разбиение множества А, то отношение r, определяемое следующим условием: аrb Û $ a: аÎАa и bÎАa, является отношением эквивалентности.
& Теорема. Отношение эквивалентности 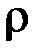 на множестве A разбивает множество A на попарно непересекающиеся подмножества (классы эквивалентности).
на множестве A разбивает множество A на попарно непересекающиеся подмножества (классы эквивалентности).
& Определение. Множество классов эквивалентности элементов множества A по эквивалентности 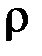 называется фактор-множеством множества A по отношению
называется фактор-множеством множества A по отношению 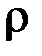 и обозначается
и обозначается 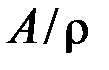 .
.
Пример
v Множество студенческих групп данного университета является фактор-множеством множества студентов вуза по отношению принадлежности к одной группе.
& Определение. Рефлексивное и транзитивное бинарное отношение на множестве A называется предпорядком на A.
& Определение. Антисимметричное и транзитивное бинарное отношение на множестве A называется порядком на A.
Пример
v На некотором множестве людей отношением предпорядка являются: а) рост одного человека больше или равен росту другого; б) вес одного человека больше или равен весу другого.
& Определение. Рефлексивное, транзитивное и антисимметричное отношение на множестве A называется нестрогим частичным порядком на A. Частичный порядок часто обозначают символом 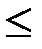 (или
(или 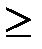 ).
).
Примеры
v Отношение £ (или ³) на множестве всех чисел.
v х кратно у, где 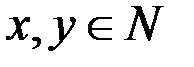 .
.
v отношение включения для множеств на множестве всех подмножеств.
& Определение. Антирефлексивное, строго антисимметричное и транзитивное отношение называется отношением строгого частичного порядка на множестве A. Строгий частичный порядок обозначают символом 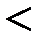 (или
(или  ).
).
& Определение. Отношение частичного порядка на множестве A, для которого любые два элемента из A сравнимы (т. е. 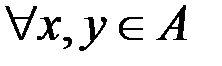 либо
либо 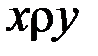 , либо
, либо 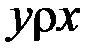 ), называется отношением линейного порядка (строгого или нестрогого).
), называется отношением линейного порядка (строгого или нестрогого).
& Определение. Множество A с заданным на нем частичным (линейным) порядком называется частично (линейно) упорядоченным.
Примеры
v Отношения « 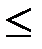 » на R, «
» на R, « 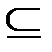 » на множестве всех множеств, «подчиненность должностей» – отношения частичного порядка на соответствующих множествах; при этом, поскольку
» на множестве всех множеств, «подчиненность должностей» – отношения частичного порядка на соответствующих множествах; при этом, поскольку 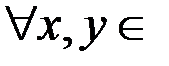 R либо
R либо 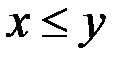 , либо
, либо 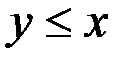 (т. е. любые два элемента сравнимы), то «
(т. е. любые два элемента сравнимы), то « 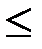 » - отношение нестрогого частичного (линейного) порядка.
» - отношение нестрогого частичного (линейного) порядка.
v Отношения « 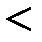 » на R, «
» на R, « 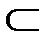 » на множестве всех множеств – отношения строгого частичного (линейного) порядка.
» на множестве всех множеств – отношения строгого частичного (линейного) порядка.
v Бинарное отношение « 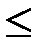 » на множестве комплексных чисел С не является отношением линейного порядка, так как ни пара (1, i), ни (i, 1) не принадлежат бинарному отношению «
» на множестве комплексных чисел С не является отношением линейного порядка, так как ни пара (1, i), ни (i, 1) не принадлежат бинарному отношению « 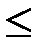 ». Аналогично бинарное отношение «
». Аналогично бинарное отношение « 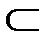 » на множестве множеств также не является линейным.
» на множестве множеств также не является линейным.
1.5. Мощность множества
& Определение. Множество A называется эквивалентным (или равномощным) множеству B (символически A ~ B), если между элементами A и B можно установить взаимно однозначное соответствие (бинарное отношение, являющееся биекцией).
Первый зародыш общего понятия равномощности появляется у Галилея, заметившего, что отображение n®n2 устанавливает биекцию между натуральными числами и их квадратами. Этот пример был приведен Галилеем в качестве контрпримера к «аксиоме»: «целое больше части». Понятие равномощных множеств было введено Больцано.
Отношение равномощности обозначается равенством 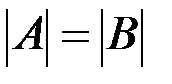 .
.
Отношение «иметь равную мощность» является отношением эквивалентности.
Обозначим через n мощность множества 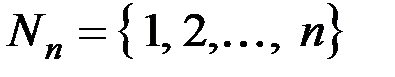 , где
, где
n - конечное натуральное число, т. е. 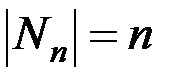 .
.
& Определение. Каждое множество A,эквивалентное 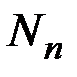 для некоторого n, называется конечным, а n - числом элементов (мощностью) множества A:
для некоторого n, называется конечным, а n - числом элементов (мощностью) множества A: 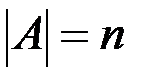 . Множество, не являющееся конечным, называется бесконечным.
. Множество, не являющееся конечным, называется бесконечным.
Конечные множества A и B равномощны тогда и только тогда, когда количество элементов множества A равно количеству элементов множества B .
Также для конечных множеств A, B, C, D справедливы следующие утверждения:
ü мощность объединения множеств A и B (т. е. число элементов, составляющих множество  - см. рис. 1.2, а), равна:
- см. рис. 1.2, а), равна:
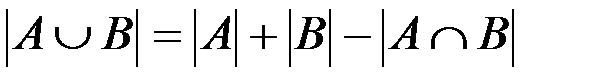 ;
;
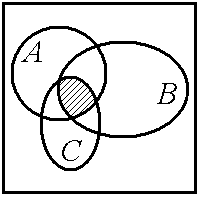
ü мощность объединения трех множеств A, B и C (см. рис. 1.5, а):
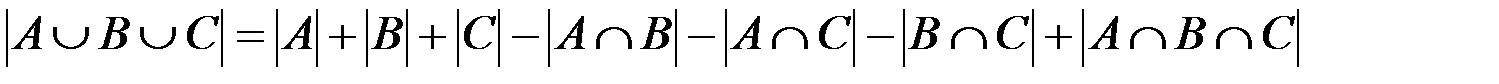 ;
;
ü в общем случае пусть A1, …, An – конечные множества, тогда для мощности объединения всех этих множеств 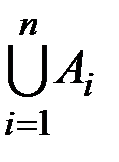 справедлива формула включений-исключений:
справедлива формула включений-исключений:
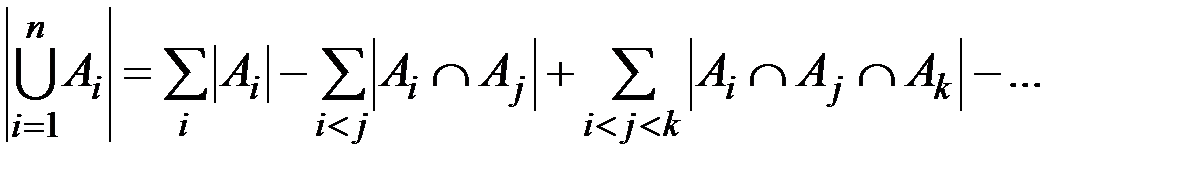
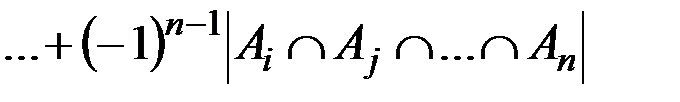 ;
;
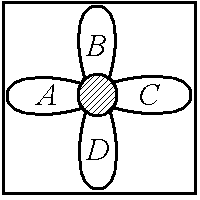
ü мощность объединения четырех множеств A, B, C и D, имеющих только общее пересечение, т. е. пересечение любой пары множеств является одновременно пересечением любой другой пары (см. рис. 1.5, б):
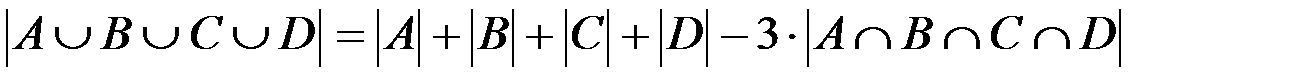 ;
;
ü мощность разности множеств A и B (см. рис. 1.3, а):
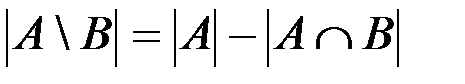 ;
;
ü мощность прямого произведения множеств A и B: 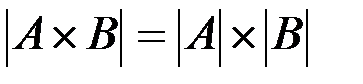 и как следствие
и как следствие 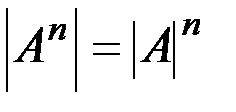 .
.
| 
|
| а | б |
Рис. 1.5. Мощности объединения:
а – трех множеств; б – четырех множеств
Далее рассмотрим свойства бесконечных множеств.
& Определение . Каждое множество A,равномощное множеству
N всех натуральных чисел, называется счетным множеством.
& Определение . Каждое множество A,эквивалентное множеству действительных чисел R, называется континуальным множеством (несчетным), и его мощность обозначается через С. Кардинальное число С называется мощностью континуума.
? Примечание. Для конечных множеств и только для них мощность связывается с числом. Мощность бесконечного множества не выражается числом, она является качественным показателем, позволяющим сравнивать бесконечные множества между собой.
Пример
v Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Найти количество студентов, занимающихся только спортом; не увлекающихся ничем.
Обозначим первой большой буквой множество студентов, увлекающихся тем или иным (например, Ж – множество студентов, увлекающихся живописью). Множество всех студентов обозначим через U. Тогда нас интересует
|(С\(ЖÈМ)| и |U\(ЖÈМÈС)|.
Из свойств операций над множествами имеем:
|С\(ЖÈМ)| = |С\((ЖÈМ)ÇС))| = |С| – |(ЖÇС)È(МÇС)| =
= |С| – (|ЖÇС| + |МÇС| – |ЖÇМÇС|) = 42 – (10 + 5 – 3) = 30.
|U\(ЖÈМÈС)| = |U| – |ЖÈМÈС| =
= 100 – (|Ж| + |М| + |C| – |ЖÇМ| – |ЖÇС| – |МÇС| + |ЖÇСÇМ|) =
= 100 – (28 + 30 + 42 – 8 – 10 – 5 + 3) = 20.
& Теорема. Любое бесконечное множество содержит счетное подмножество.
Доказательство. Пусть A – бесконечное множество. Выберем элемент a1ÎA (A не пусто, так как оно бесконечно), затем выберем элемент a2ÎA\{a1} (A\{a1} не пусто, так как A бесконечно) и т. д. В результате из выбранных элементов получим множество A1 = {a1,a2,…,an,…}, каждому элементу которого сопоставлено натуральное число n (порядковый номер элемента). Следовательно, |A1| = |N|, т. е. A1 – счетное множество.
Любое бесконечное B счетного множества A счетно.
Объединение конечного или счетного семейства счетных множеств является счетным множеством.
Если множество A является бесконечным, то существует его подмножество В такое, что В¹A и В равномощно с A. Если A и B счетные, то A × B – счетное множество.
Множество рациональных чисел Q является счетным.
Множество точек интервала (0,1) является несчетным.
& Теорема. Пусть для множеств А и В существуют множества А1ÍА и В1ÍВ такие, что множество А равномощно с В1, а множество В с А1, то множества А и В равномощны.
& Определение . Считается, что мощность множества A не превосходит мощности множества B, т. е. 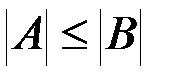 , если A равномощно некоторому подмножеству множества B, т. е. существует множество
, если A равномощно некоторому подмножеству множества B, т. е. существует множество 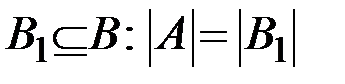 .
.
Отношения 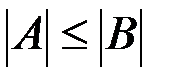
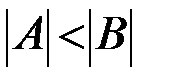 на совокупности множеств есть отношения нестрогого и строгого частичного (линейного) порядка.
на совокупности множеств есть отношения нестрогого и строгого частичного (линейного) порядка.
& Определение. Если 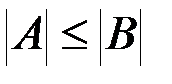 и множества A и B не равномощны, то имеет место строгое неравенство
и множества A и B не равномощны, то имеет место строгое неравенство 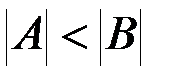 .
.
& Теорема.Пусть Х и Y два множества такие, что Х¹Æ, Y¹Æ и в Y не менее двух элементов. Тогда множество всех функций, действующих из Х в Y, является множеством, мощность которого больше мощности множества Х.
& Утверждение.
1. |Nn| < |N| < C.
2. 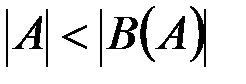 .
.
? Следствие. Поскольку для каждого множества существует Булеан, а для Булеана - свой Булеан, то не существует самого мощного множества. При этом |B(R)| > |R|, но |B(N)| = |R|.
Примеры
v Если 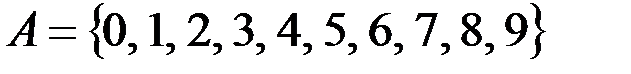 , то
, то 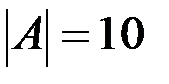 .
.
v Множество 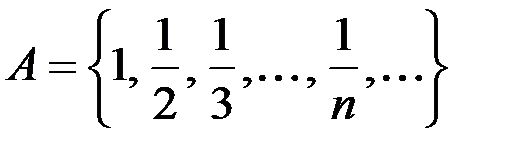 – cчетно, поскольку является равномощным множеству N; для доказательства эквивалентности необходимо указать биекцию (взаимнооднозначное соответствие между А и N)
– cчетно, поскольку является равномощным множеству N; для доказательства эквивалентности необходимо указать биекцию (взаимнооднозначное соответствие между А и N) 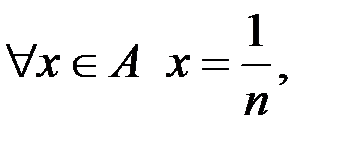 где
где 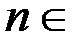 N.
N.
v Множество 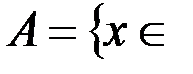 R
R 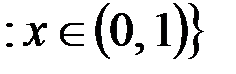 – несчетно, поскольку является эквивалентным множеству R:
– несчетно, поскольку является эквивалентным множеству R: 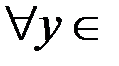 R
R 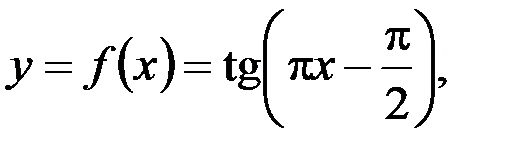
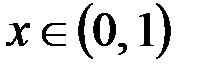 .
.
v Для построения биекции между отрезком [0,1] и интервалом (0,1) надо помнить о несчетности рассматриваемых множеств. Идея решения: из интервала (0,1) выделяют некоторое счетное множество А. Затем к нему добавляют две точки {0} и {1}. Вновь полученное множество (обозначим его ВÌ[0,1]), также является счетным. Значит, множества А и В равномощны и существует биекция f, отображающая B на A. Построим теперь биекцию отрезка [0,1] на интервал (0,1) следующим образом: 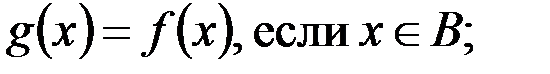
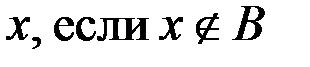 .
.
v Интервал (0,1) и полуинтервал (0,1] равномощны. Для доказательства воспользуемся известными сведениями про счетные множества. Выделим в интервале какое-нибудь счетное подмножество, например A = {1/2, 1/3, 1/4, 1/5, ...}. Если добавим к нему точку 1, то оно останется счетным: A∪{1}={1, 1/2, 1/3, 1/4, ...}. Таким образом, существует биекция f из множества A в множество A∪{1}. Теперь нетрудно доопределить f до биекции всего интервала (0,1) в полуинтервал (0,1]. Для этого скажем, что все точки, на которых f пока не определено, т. е. все точки из (0,1)\A, переходят в себя: f(x) = x. Можно записать это формулой: f(x) = 1/(n − 1), если 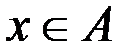 и x = 1/n при n ≥ 2; x, если
и x = 1/n при n ≥ 2; x, если 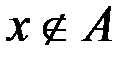 .
.
1.6. Элементы комбинаторики
Пусть есть некоторое конечное множество элементов
U = {a1, a2, ..., an}.
Рассмотрим набор элементов
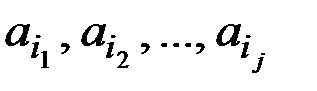 , где
, где 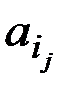 ÎU, j = 1, 2, ..., r.
ÎU, j = 1, 2, ..., r.
Этот набор называется выборкой объема r из n элементов.
Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).
Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным условиям, т. е. выбор производится по какому-нибудь принципу. Подсчет числа выборок основывается на двух правилах теории множеств.
& Определение. Принцип суммы: если объект A можно выбрать m способами, объект B другими n способами и их одновременный выбор невозможен, то выбор «A или B» может быть осуществлен m + n способами.
& Определение. Принцип произведения: если объект A может быть выбран m способами, при любом выборе A объект B может быть выбран n способами, то выбор «A и B» может быть осуществлен m × n способами.
Пример
v Бросают 2 игральные кости. Сколькими способами они могут выпасть так, что на обеих костях выпадет четное число очков либо на обеих костях выпадет нечетное число очков?
Пусть m – число возможностей для выпадения четного числа на одной кости, n – число возможностей для выпадения нечетного числа. Здесь m = n = 3. По правилу произведения количество выпадения четных чисел, как и нечетных, на обеих костях: 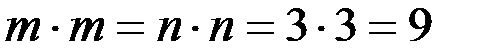 . По правилу суммы количество возможностей для выпадения двух четных или двух нечетных чисел будет 9 + 9 = 18.
. По правилу суммы количество возможностей для выпадения двух четных или двух нечетных чисел будет 9 + 9 = 18.
& Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов не существенен, то выборка называется неупорядоченной.
Из определения следует, что две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.
& Определение. Упорядоченные выборки, объемом n из n элементов, где все элементы различны, называются перестановками из n элементов. Число перестановок из n элементов обозначается Pn.
P = n!.
Пример
v Сколько существует способов расположения на полке 10 различных книг? P = 10! Можно рассуждать иначе. Выбираем первый элемент, это можно сделать n способами. Затем выбираем второй элемент, это можно сделать (n-1) способами. По правилу произведения упорядоченный выбор двух элементов можно осуществить n´(n-1) способами. Затем выбираем третий элемент, для его выбора останется n-2 возможности, последний элемент можно выбрать единственным способом. Вновь приходим к формуле: 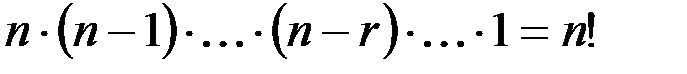 .
.
& Определение. Упорядоченные выборки объемом m из n элементов (m<n), где все элементы различны, называются размещениями. Число размещений из n элементов по m обозначается 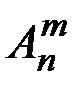 .
.
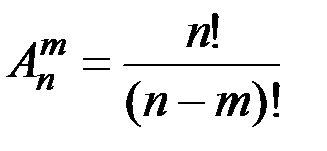 .
.
Выведем эту формулу. Первый элемент выбираем n способами, второй – (n – 1) способами и т. д., m-й элемент выбираем
(n – m + 1) способом. По принципу произведения имеем:
 =
= 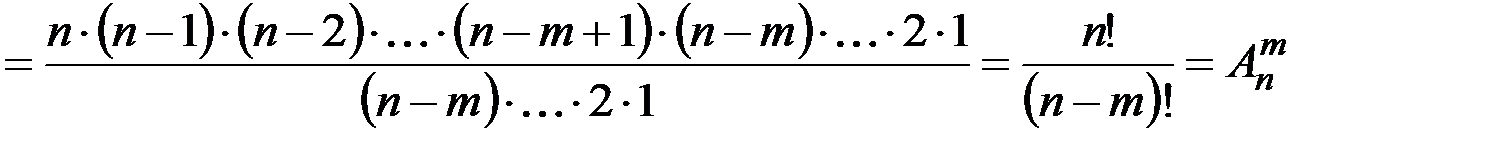 .
.
Пример
v Группа из 15 человек выиграла 3 различные книги. Сколькими способами можно распределить эти книги среди группы? Имеем 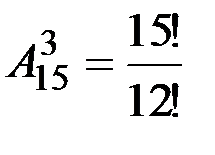 = 15×14×13 = 2730.
= 15×14×13 = 2730.
& Определение. Неупорядоченные выборки объемом m из n элементов (m<n) называются сочетаниями. Их число обозначается 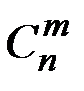 .
.
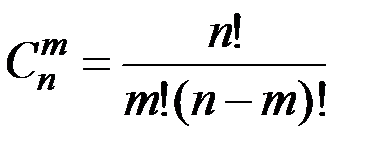 .
.
Выведем эту формулу. Очевидно, 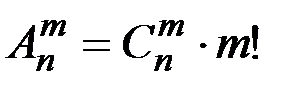 . Действительно, объект A – неупорядоченная выборка из n элементов по m, их число
. Действительно, объект A – неупорядоченная выборка из n элементов по m, их число 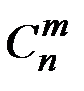 . После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает «порядок» в выборке). Совместный выбор «A и B» – упорядоченная выборка.
. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает «порядок» в выборке). Совместный выбор «A и B» – упорядоченная выборка.
Пример
v Группа из 15 человек выиграла 3 одинаковые книги. Сколькими способами можно распределить эти книги среди группы? 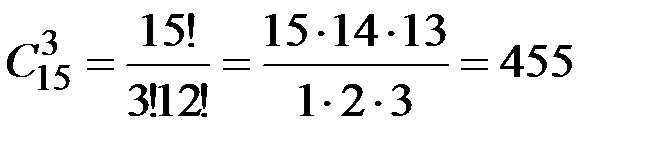 .
.
& Определение. Числа 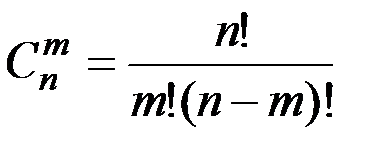 называются биноминальными коэффициентами.
называются биноминальными коэффициентами.
Исходя из определения справедлива следующая формула
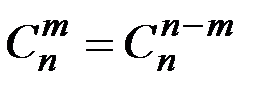 .
.
Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.
& Определение. Упорядоченные выборки объемом m из n элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается 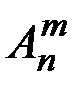 (n).
(n).
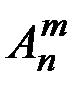 (n) = nm.
(n) = nm.
Вывод формулы: первый элемент может быть выбран n способами, второй – также n способами и т. д., m-й элемент также может быть выбран n способами. По принципу произведения получаем nm.
Пример
v Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций? n = 10, m = 4 и ответом будет 104.
& Определение. Пусть имеется n элементов, среди которых k1 элементов первого типа, k2 элементов второго типа и т. д., ks элементов s-го типа, причем k1 + k2 +...+ ks = n. Упорядоченные выборки из таких n элементов по n называются перестановками с повторениями. Их число обозначается C n(k1,k2,...,ks). Числа C n(k1,k2,...,ks) называются полиномиальными коэффициентами.
Cn(k1,...,ks) = 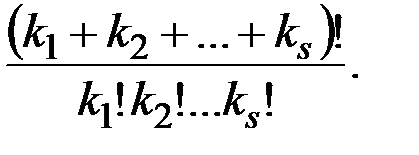
Вывод формулы. Если считать все 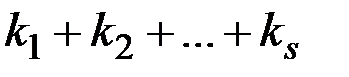 элементов перестановки с повторениями различными, то всего различных вариантов перестановок
элементов перестановки с повторениями различными, то всего различных вариантов перестановок 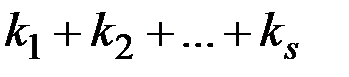 элементов –
элементов – 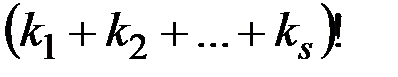 . Однако среди этих перестановок не все различны. В самом деле, все элементы первого типа можно переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же можем переставлять элементы второго и до s-го типа. Таким образом, всякая перестановка может быть записана
. Однако среди этих перестановок не все различны. В самом деле, все элементы первого типа можно переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же можем переставлять элементы второго и до s-го типа. Таким образом, всякая перестановка может быть записана 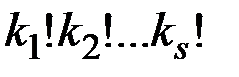 способами. Следовательно, число различных перестановок с повторениями равно
способами. Следовательно, число различных перестановок с повторениями равно
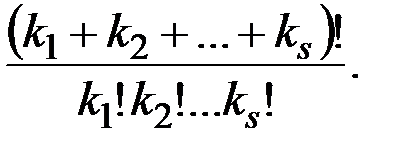
Пример
v Сколько различных слов можно получить, переставляя буквы в слове «математика»? Буква «а» входит 3 раза (k1 = 3), буква «м» – 2 раза (k2 = 2), «т» – 2 раза (k3 = 2), буквы «е», «к», «и» входят по одному разу, отсюда k3 = k4 = k5 = 1. С10(3,2,2,1,1,1) = 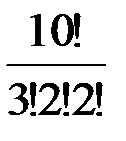 = 151200.
= 151200.
& Определение. Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m´n) называется сочетанием с повторением.
Число сочетаний с повторениями обозначается 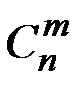 (n).
(n).
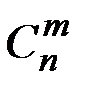 (n) =
(n) = 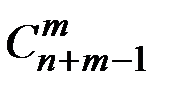 .
.
Пример
v В кондитерской имеется 4 вида пирожных: наполеон, эклер, песочное и картошка. Покупатель берет 7 пирожных. Сколькими способами он может это сделать? (Предполагается, что пирожных каждого вида ³ 7).
Число способов будет 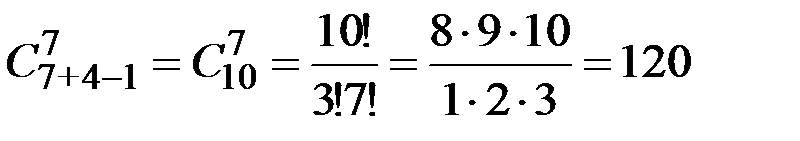 .
.
Решить задачу можно следующим образом. Пирожные кладутся в коробку и разделяются картонными разделителями. Для 4-х типов пирожных необходимо 3 разделителя. Обозначим разделители 0 и 1 – пирожные.
Пример покупки: 1110101101 – три наполеона, 1 эклер, 2 песочных и 1 картошка. Итак, два класса объектов 1 (7 штук) и 0 (3 штуки) – покупка – 10 объектов.
Теперь задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов: 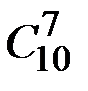 .
.
Пример
v Пусть V = {a, b, c}. Объем выборки m = 2. Перечислить размещения, сочетания, размещения с повторениями, сочетания с повторениями.
1. Размещения: {(ab), (b c), (ac), (ba), (cb), (ca)}. 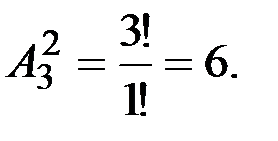
2. Сочетания: {(ab), (ac), (bc)}. 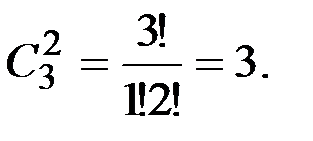
3. Размещения с повторениями: {(ab), (bc), (ac), (ba), (cb), (ca), (aa), (bb), (cc)}. 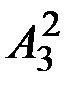 (3) = 32 = 9.
(3) = 32 = 9.
4. Сочетания с повторениями: {(ab), (bc), (ca), (aa), (bb), (cc)}. 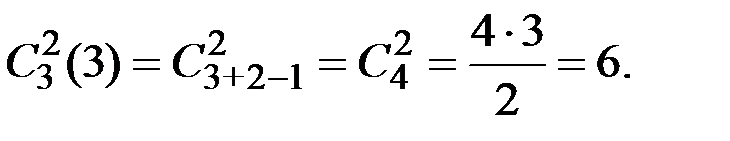
1.7. Практические задания
Множества
Задание 1. Обозначим множества A, B, C, D через геометрические фигуры:
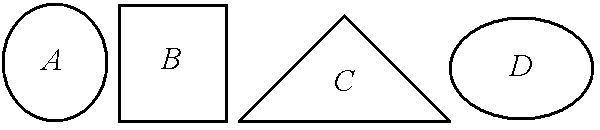
Рис. 1.6. Геометрические фигуры для построения выражений
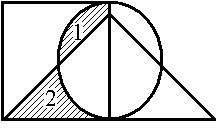
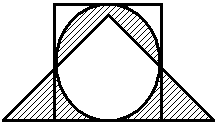
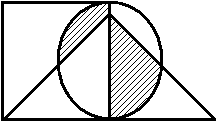
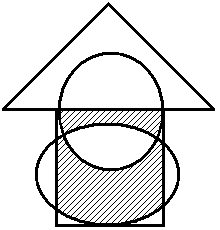
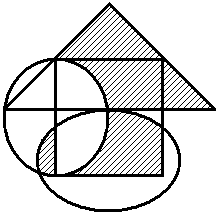
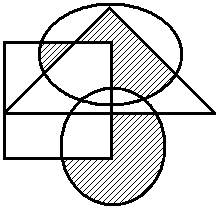
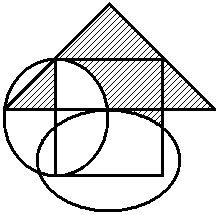
Построить выражение над множествами A, B и C, которому соответствует заштрихованная область на диаграммах Эйлера–Венна:
| 
| 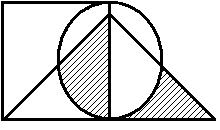
| 
|
| а | б | в | г |
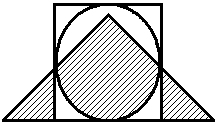
| 
| 
| 
|
| д | е | ж | з |
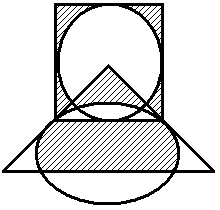
| 
| 
| 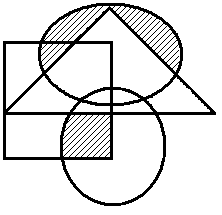
|
| и | к | л | м |
Рис. 1.7. Геометрические фигуры для выполнения Задания 1
Задание 2.
1) Равны ли множества:
а. {{1, 2}, {2, 3}} и {1, 2, 3}.
б. {{1, 2}} и {1, 2}.
в. {x: xÎN и x < 5} и {x: xÎN и (x + 1)2 < 29}.
2) Верно ли, что {1, 2}Î{{1, 2, 3}, {1, 3}, 1, 2}.
3) Привести пример множеств A, B, C: AÎB, BÎC, но AÏC.
Задание 3. Доказать с использованием теоретико-множественного аппарата:
а. 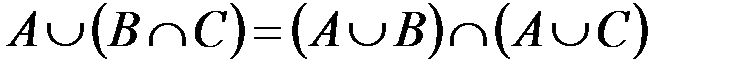 .
.
б. 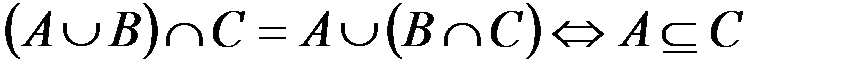 .
.
в. 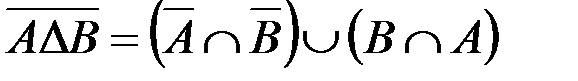 .
.
г. 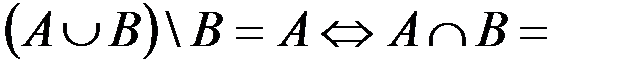 Æ.
Æ.
д. 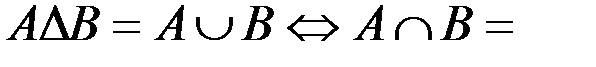 Æ.
Æ.
е. 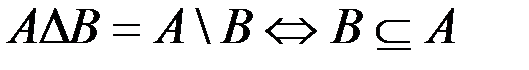 .
.
ж. 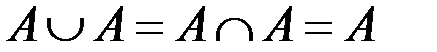 .
.
з. 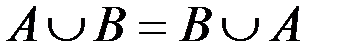 .
.
и. 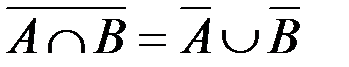 .
.
к. 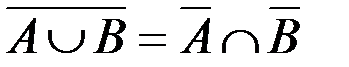 .
.
л. 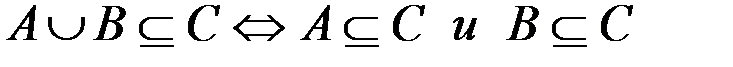 .
.
м. 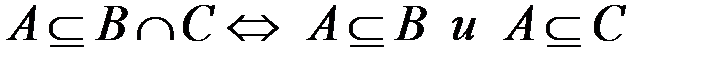 .
.
н. 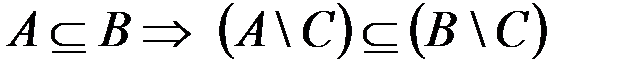 .
.
о. 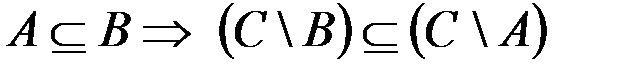 .
.
Задание 4. Доказать с использованием алгебры множеств:
а. 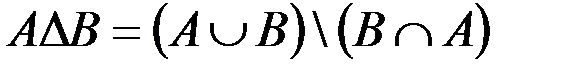 .
.
б. 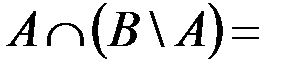 Æ.
Æ.
в. 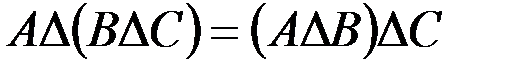 .
.
г. 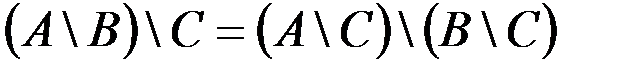 .
.
Задание 5. Решить системы уравнений:
а. 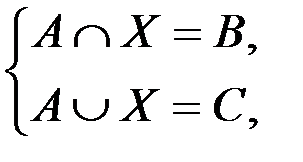 где А, В, С – множества и ВÍАÍС.
где А, В, С – множества и ВÍАÍС.
б. 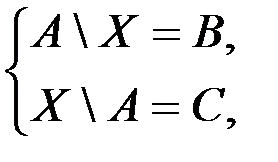 где А, В, С – множества и ВÍА, АÇС = Æ.
где А, В, С – множества и ВÍА, АÇС = Æ.
в. 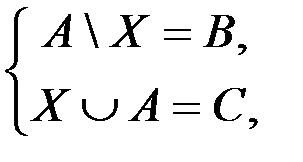 где А, В, С – данные множества и ВÍАÍС.
где А, В, С – данные множества и ВÍАÍС.
Отношения и функции
Задание 1. Доказать (A, B, C и D не пусты):
а. 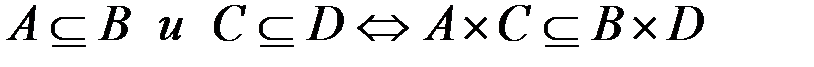 .
.
б. 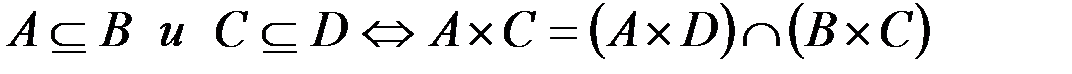 .
.
в. 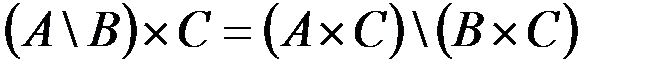 .
.
г. 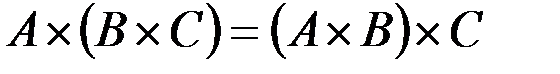 .
.
д. 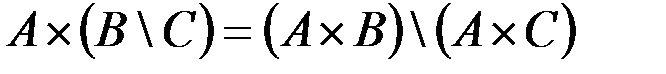 .
.
е. 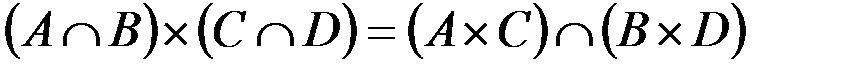 .
.
ж. 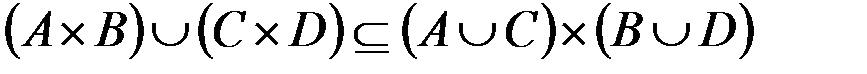 .
.
Задание 2. Найти области определения и значений Dr и Rr, обратное отношение 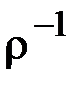 , композиции
, композиции 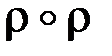 ,
, 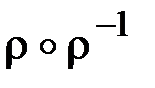 ,
, 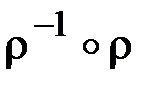 для отношений:
для отношений:
а . 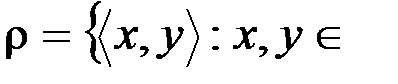 R
R 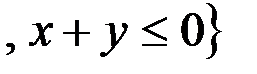 .
.
б . 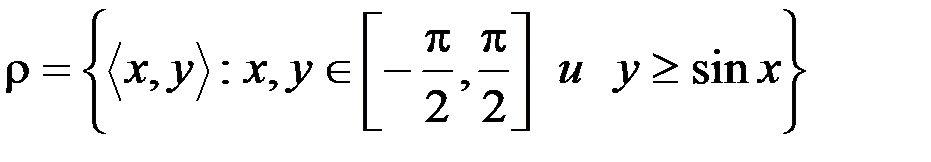 .
.
в . 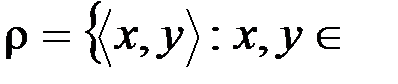 R
R 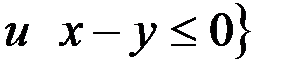 .
.
г . 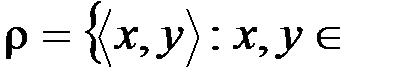 R
R 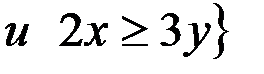 .
.
д . 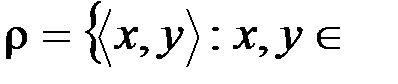 N
N 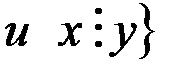 .
.
е . 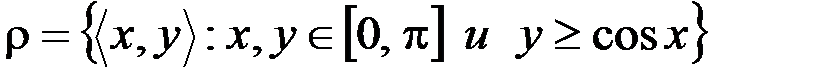 .
.
Задание 3. Доказать:
а. 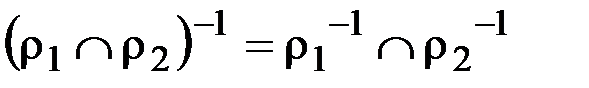 (для
(для 
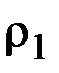 и
и 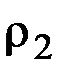 ).
).
б. 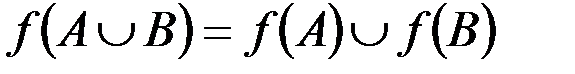 (для
(для  f).
f).
в. 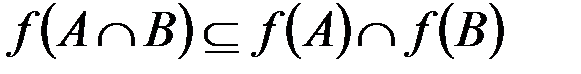 (для
(для  f).
f).
г. Если 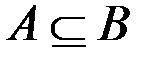 , то
, то 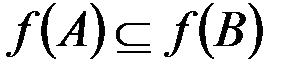 (для
(для  f).
f).
д. 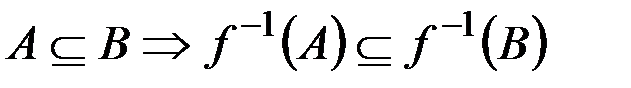 .
.
Задание 4. Доказать, что отношение
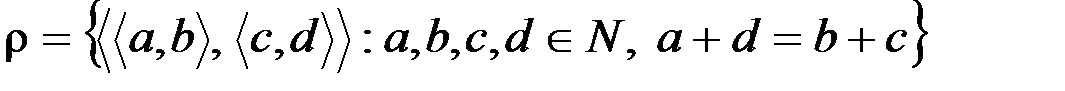 ,
,
является отношением эквивалентности.
Задание 5. Исследовать следующие отношения на рефлексивность, симметричность, транзитивность. Являются ли они отношениями эквивалентности или частичного порядка, линейного порядка?
| а. отношение параллельности прямых на множестве всех прямых на плоскости; |
| б. отношение перпендикулярности прямых на множестве всех прямых на плоскости; |
| в. отношение концентричности на множестве окружностей; |
| г. отношение «быть кратным» на множестве натуральных чисел; |
| д. отношение «быть не выше» на множестве людей; |
| е. отношение «быть выше» на множестве людей; |
| ж. отношение «иметь разный цвет» на некотором множестве цветных предметов; |
| з. отношение «быть зеркальным отражением» на множестве плоских геометрических фигур; |
| и. отношение равномощности бесконечных множеств. |
Мощность множества
Задание 1.
а. В одном жестоком бою из 100 смелых пиратов 70 потеряли ногу, у 75 отсекли руку, 80 стали одноглазыми, а 85 остались с одним ухом. Доказать, что как минимум 10 пиратов потеряли и ногу, и руку, и глаз, и ухо.
б. Пусть A – множество натуральных чисел от 1 до 1000, остаток от деления которых на 3 равен 1; B – множество натуральных чисел от 1 до 1000, остаток от деления которых на 4 равен 3. Найти количество элементов множества 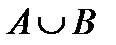 .
.
в. Даны множества N1 = {натуральные числа от 1 до 1000, нацело делящиеся на 30}, N2 = {натуральные числа от 1 до 1000, нацело делящиеся на 42}, N3 = {натуральные числа от 1 до 1000, нацело делящиеся на 105}. Найти количество элементов множества 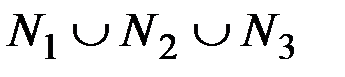 .
.
г. В актовом зале университета на празднование 23 февраля собрали студентов первого, второго и третьего курсов. Студентки второго курса дежурили по столовой и отсутствовали первые двадцать минут. В это время в зале было занято 347 мест. После собрания студенты первого и второго курса были отправлены на подготовку спортзала для проведения соревнований. В зале осталось занятыми 125 мест. Всего в соревнованиях участвовало 308 студентов: все первокурсники и юноши второго и третьего курсов. Сколько юношей обучалось на третьем курсе?
д. Пусть универсальное множество состоит из натуральных чисел от 1 до 1000; множество A – множество чисел, остаток от деления которых на 3 равен 1; множество B – множество чисел, остаток от деления которых на 5 равен 2; множество C – множество чисел, остаток от деления которых на 7 равен 4. Найти количество элементов множеств: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 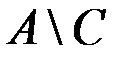 .
.
е. В условиях задания 1 в найти количество элементов, содержащихся во множестве:
1) 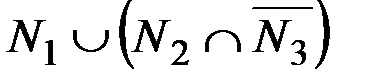 ; 2)
; 2) 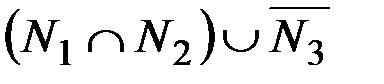 ; 3)
; 3) 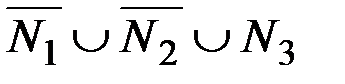 ;
;
4) 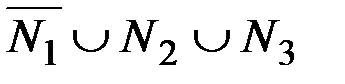 .
.
ж. В микрорайоне «Высотный» есть кирпичные и панельные дома высотой в 9, 12 и 16 этажей, причем дома высотой более чем в 9 этажей считаются элитными. До 2003 года панельные дома строили лишь 9 и 12-этажные. В это время микрорайон состоял из 24 домов. С 2003 по 2005 годы строили только 16-этажные панельные дома. К концу 2005 года в микрорайоне уже было выстроено 25 16-этажных домов (с учетом новых панельных). Известно, что среди 12-этажных домов есть 5 кирпичных. Сколько домов в микрорайоне «Высотный», если там построено 18 кирпичных элитных домов?
з. В спортивном клубе «Чемпион» в секциях по волейболу, баскетболу и теннису занимаются 57 спортсменов. Занятия по волейболу и теннису начинаются позже остальных, поэтому с утра в клубе занимались 28 человек. Затем подошли все спортсменки и мужчины из секции по теннису. В этот момент в клубе находилось 45 человек. Известно, что в клубе состоят 25 мужчин, не занимающихся теннисом. Сколько женщин в «Чемпионе» занимаются баскетболом?
Задание 2. Доказать равномощность множеств:
а. [0,1] и (0,1);
б. [a,b] и [c,d] при a < b, c < d;
в. 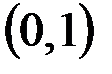 и
и 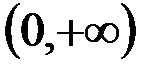 ;
;
г. 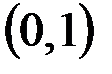 и R;
и R;
д. [a,b] иR;
е. (0,1), [0,1) и (0,1];
ж. 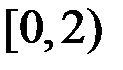 и
и 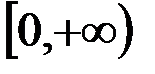 ;
;
з. 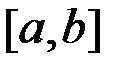 и
и 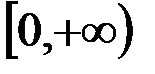 ;
;
и. 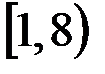 и
и 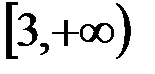 ;
;
к. 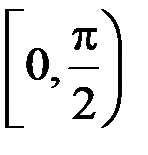 и
и 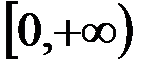 ;
;
л. 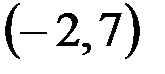 и R;
и R;
м. 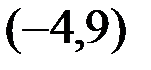 и
и 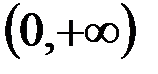 .
.
Элементы комбинаторики
1. Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из одиннадцати дисциплин.
2. Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распределять между собой обязанности?
3. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
4. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
5. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
6. Номера трамвайных маршрутов иногда обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?
7. Чемпионат, в котором участвуют 16 команд, проводится в два круга (т. е. каждая команда дважды встречается с любой другой). Определить, какое количество встреч следует провести.
8. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти цифр. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?
9. Из группы в 15 человек выбирают четырех участников эстафеты 800 + 400 + 200 + 100. Сколькими способами можно расставить спортсменов по этапам эстафеты?
10. Команда из пяти человек выступает на соревнованиях по плаванию, в которых участвуют еще 20 спортсменов. Сколькими способами могут распределиться места, занятые членами этой команды?
11. Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находиться с ней на одной горизонтали или на одной вертикали шахматной доски.)
12. Две ладьи различного цвета расположены на шахматной доске так, что каждая может взять другую. Сколько существует таких расположений?
13. Порядок выступления восьми участников конкурса определяется жребием. Сколько различных исходов жеребьевки при этом возможно?
14. 30 человек разбиты на 3 группы по 10 человек в каждой. Сколько может быть различных составов групп?
15. Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 3, 5, 7, если каждое число не должно содержать одинаковых цифр?
16. Сколько различных светящихся колец можно сделать, расположив по окружности 10 разноцветных лампочек (кольца считаются одинаковыми при одинаковом порядке следования цветов)?
17. На книжной полке помещается 30 томов книг. Сколькими способами их можно расставить, чтобы при этом первый и второй тома не стояли рядом?
18. Четыре стрелка должны поразить восемь мишеней (каждый по две). Сколькими способами они могут распределить мишени между собой?
19. Из группы в 12 человек ежедневно в течение 6 дней выбирают двух дежурных. Определить количество различных списков дежурных, если каждый человек дежурит один раз.
20. Сколько 4-хзначных чисел, составленных из цифр 0, 1, 2, 3, 4, 5, содержат цифру 3 (цифры в числах не повторяются)?
21. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы №1 и №2 находились бы в соседних аудиториях?
22. В турнире участвуют 16 шахматистов. Определить количество различных расписаний первого тура (расписания считаются различными, если отличаются участниками хотя бы одной партии; цвет фигур и номер доски не учитываются).
23. Шесть ящиков различных материалов доставляются на пять этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на пятый этаж доставлен какой-либо один материал?
24. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
25. Поезд метро делает 16 остановок, на которых выходят все пассажиры. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке?
26. Сколько трехзначных чисел, делящихся на 3, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр?
27. Собрание из 80 человек избирает председателя, секретаря и трех членов ревизионной комиссии. Сколькими способами это можно сделать?
28. Из 10 теннисисток и 6 теннисистов составляют 4 смешанные пары. Сколькими способами это можно сделать?
29. Три автомашины №1,2,3 должны доставить товар в шесть магазинов. Сколькими способами можно использовать машины, если грузоподъемность каждой из них позволяет взять товар сразу для всех магазинов и если две машины в один и тот же магазин не направляются? Сколько вариантов маршрута возможно, если решено использовать только машину №1?
30. Четверо юношей и две девушки выбирают спортивную секцию. В секцию хоккея и бокса принимают только юношей, в секцию художественной гимнастики – только девушек, а в лыжную и конькобежную секции – и юношей, и девушек. Сколькими способами могут распределиться между секциями эти шесть человек?
31. Из лаборатории, в которой работает 20 человек, 5 сотрудников должны уехать в командировку. Сколько может быть различных составов этой группы, если начальник лаборатории, его заместитель и главный инженер одновременно уезжать не должны?
32. В фортепьянном кружке занимаются 10 человек, в кружке художественного слова – 15, в вокальном кружке – 12, в фотокружке – 20 человек. Сколькими способами можно составить бригаду из четырех чтецов, трех пианистов, пяти певцов и одного фотографа?
33. Двадцать восемь костей домино распределены между четырьмя игроками. Сколько возможно различных распределений?
34. Сколькими способами из группы в 15 человек могут быть выделены бригадир и 4 члена бригады?
35. Сколькими способами можно 5 учеников распределить по 3 параллельным классам?
36. Лифт останавливается на 10 этажах. Сколькими способами могут распределиться между этими остановками 8 пассажиров, находящихся в лифте?
37. Восемь авторов должны написать книгу из шестнадцати глав. Сколькими способами возможно распределение материала между авторами, если два человека напишут по три главы, четыре – по две, два – по одной главе книги?
38. В шахматном турнире участвуют 8 шахматистов третьего разряда, 6 – второго и 2 перворазрядника. Определить количество таких составов первого тура, чтобы шахматисты одной категории встречались между собой (цвет фигур не учитывается).
39. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа: не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
40. 8 яблок и 2 апельсина надо положить в 2 пакета так, чтобы в каждом пакете был хотя бы 1 апельсин и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?
41. Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?
42. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?
43. Садовник должен в течение трех дней посадить 10 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?
44. Из вазы, где стоят 10 красных и 4 розовых гвоздики, выбирают один красный и два розовых цветка. Сколькими способами это можно сделать?
45. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
46. Каждый из десяти радистов пункта А старается установить связь с каждым из двадцати радистов пункта Б. Сколько возможно различных вариантов такой связи?
47. 6 ящиков различных материалов доставляют на 8 этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на 8-й этаж попадет не более 2-х материалов?
48. Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд так, чтобы при этом два футболиста одной команды не стояли рядом?
49. На книжной полке книги по математике и по логике – всего 20 книг. Показать, что наибольшее количество вариантов комплекта, содержащего 5 книг по математике и 5 книг по логике, возможно в том случае, когда число книг на полке по каждому предмету равно 10.
50. Лифт, в котором находятся 9 пассажиров, может останавливаться на десяти этажах. Пассажиры группами выходят по два, три и четыре человека. Сколькими способами это может произойти?
1.8 Задания в тестовой форме
ВАРИАНТ 1
1. Способ задания множеств, при котором строятся диаграммы Эйлера–Венна
| 1. | перечисление всех элементов | 3. | задание порождающей процедурой |
| 2. | изображение элементов на плоскости | 4. | задание арифметическими операциями |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
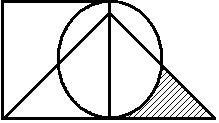
| 1. | 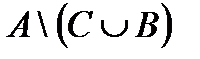
| 3. | 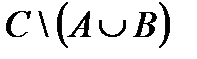
|
| 2. | 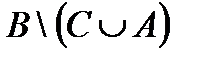
| 4. | 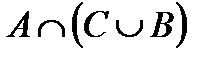
|
3. Множество нечетных чисел есть __________ подмножество множества целых чисел (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 1 | 3 | 2 | 4 | 8 | 5 | 3 | 6 | 9 | 7 |
| y | 8 | 2 | 2 | 1 | 7 | 6 | 3 | 9 | 6 | 5 |
Приведенное бинарное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть зеркальным отражением на множестве геометрических фигур (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | антисимметричное |
| 2. | не симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 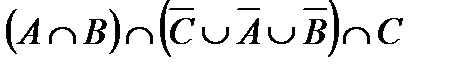
| 1. | 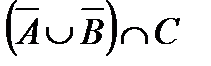
| 3. | 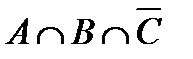
|
| 2. | 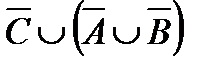
| 4. | Æ |
7. Мощность множества 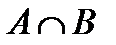 , если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 3 | 2. | 5 | 3. | 13 | 4. | 8 |
8. Найти биективное отображение 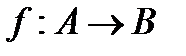 , если,
, если, 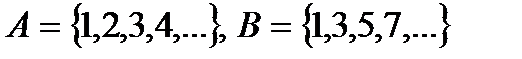
(  )
)
| 1. | |A| = |B|, y = 2x + 1 | 3. | |A| = |B|, y = 2x – 1 |
| 2. | |A| = |B|, y = x + 1 | 4. | |A| = |B|, y = 2(x – 1) |
9. Количество вариантов, которыми можно извлечь из 7 различных учебников 4, равно
| 1. | 35 | 2. | 70 | 3. | 840 | 4. | 140 |
10. Флаг составляется из 13 горизонтальных полос трех цветов: красного, белого и голубого цвета, причем любые две соседние полосы должны быть разных цветов. Количество вариантов, при которых это возможно, равно
| 1. | 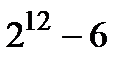
| 2. | 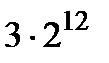
| 3. | 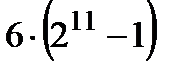
| 4. | 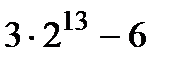
|
ВАРИАНТ 2
1. Способ задания множеств, при котором указываются общие свойства всех элементов
| 1. | перечисление всех элементов | 3. | табличный способ |
| 2. | изображение элементов на плоскости | 4. | аналитический |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.

| 1. | 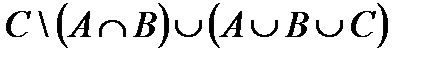
| 3. | 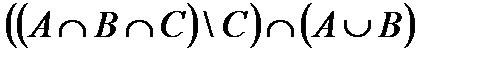
|
| 2. | 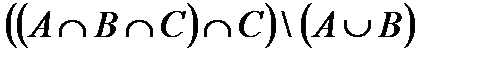
| 4. | 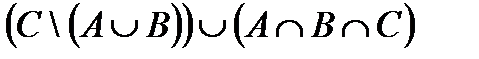
|
3. Подмножество любого множества есть ___________ множество (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{1,...,8}, yÎ{1,...,9}
| x | 4 | 1 | 3 | 2 | 8 | 5 | 3 | 6 | 1 | 7 |
| y | 6 | 9 | 7 | 8 | 2 | 5 | 7 | 4 | 9 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения коаксиальность на множестве круго-цилиндрических поверхностей (коаксиальными называются поверхности вида кругового цилиндра, имеющие общую ось) (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 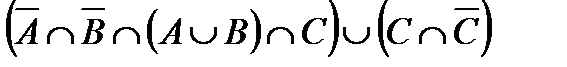
| 1. | 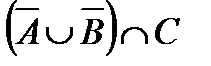
| 3. | Æ |
| 2. | 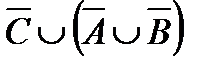
| 4. | С |
7. Мощность множества 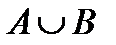 , если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 3 | 2. | 5 | 3. | 13 | 4. | 8 |
8. Найти биективное отображение 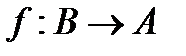 , если
, если 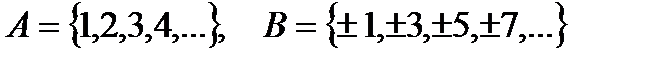
( 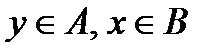 )
)
| 1. | |A| = |B|, 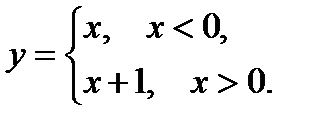
| 3. | |A| = |B|, y = 2|x| – 1 |
| 2. | |A| = |B|, 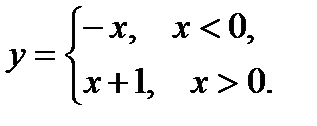
| 4. | |A| = |B|, |y| = 2(x – 1) |
9. Количество способов, которыми можно выбрать из 40 участников конференции делегацию, состоящую из 4 человек, равно
| 1. | 40×39×38×37 | 2. | 10×13×19×37 | 3. | 5×13×19×37 | 4. | 10×39×38×37 |
10. Количество способов, которыми можно n одинаковых шаров разложить в r различных ящиков, равно
| 1. | 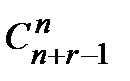
| 2. | 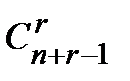
| 3. | 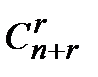
| 4. | 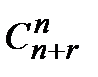
|
ВАРИАНТ 3
1. Любая совокупность определенных и различимых между собой объектов, мыслимых как единое целое
| 1. | группа | 2. | множество | 3. | класс | 4. | подгруппа |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
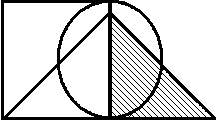
| 1. | 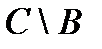
| 3. | 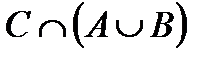
|
| 2. | 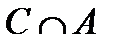
| 4. | 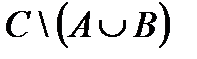
|
3. Поставьте знак отношения, в котором находятся указанные элементы и множество
3,4 ___ {1,2,3,4,5}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 1 | 3 | 2 | 4 | 8 | 5 | 3 | 6 | 9 | 7 |
| y | 8 | 2 | 3 | 1 | 7 | 6 | 2 | 8 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения неконцентричность на множестве окружностей (концентричными называются окружности, имеющие общий центр) (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | антисимметричное |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 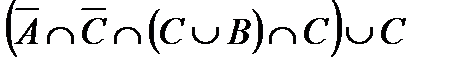
| 1. | 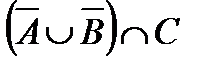
| 2. | 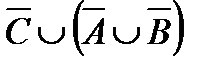
| 3. | Æ | 4. | С |
7. Мощность множества 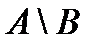 , если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 3 | 2. | 5 | 3. | 13 | 4. | 8 |
8. Найти биективное отображение 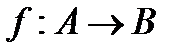 , если
, если 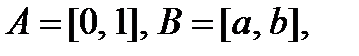
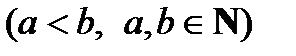
(  )
)
| 1. | |A| = |B|, y = bx – a(x – 1) | 3. | |A| = |B|, y = a – (b + a)x |
| 2. | |A| = |B|, y = a – (b – a)x | 4. | |A| = |B|, y = bx + a(x – 1) |
9. Количество способов, которыми можно взять из 8 различных красок 6, равно
| 1. | 56 | 2. | 48 | 3. | 28 | 4. | 36 |
10. Количество способов, которыми можно n одинаковых шаров разложить в r различных ящиков, если в каждом ящике должен лежать хотя бы один шар, равно
| 1. | 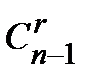
| 2. | 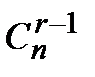
| 3. | 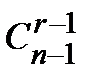
| 4. | 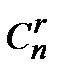
|
ВАРИАНТ 4
1. Множество, содержащее конечное число элементов, называется
| 1. | простым | 2. | составным | 3. | конечным | 4. | пустым |
 2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
| 1. | 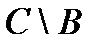
| 3. | 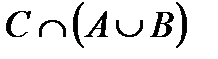
|
| 2. | 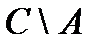
| 4. | 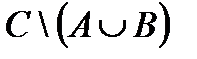
|
3. Поставьте знак отношения, в котором находятся указанные элементы и множества
{2},{3},5 ___ {{1},{2},{3},{4},{5}, 5,10}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 3 | 8 | 1 | 2 | 4 | 5 | 8 | 6 | 9 | 7 |
| y | 2 | 7 | 8 | 3 | 1 | 6 | 7 | 7 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | является функцией |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения некоаксиальность на множестве круго-цилиндрических поверхностей (коаксиальными называются поверхности вида кругового цилиндра, имеющие общую ось) (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 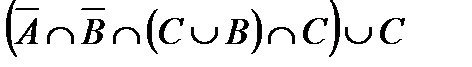
| 1. | 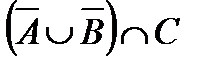
| 2. | 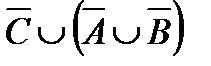
| 3. | С | 4. | Æ |
7. Мощность множества 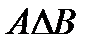 , если А = {x: xÎN и 4 < x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и 4 < x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 3 | 2. | 5 | 3. | 7 | 4. | 8 |
8. Найти биективное отображение 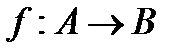 , если
, если 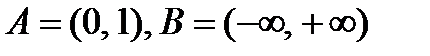 (
(  )
)
| 1. | y = tg(px) | 2. | y = сtg(px) | 3. | y = – ctg(px) | 4. | y = – tg(px) |
9. Число перестановок из n элементов обозначается
| 1. | 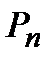
| 2. | 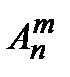
| 3. | 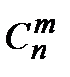
| 4. | 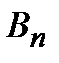
|
10. Количество способов, которыми можно сделать 4-хцветный флаг с горизонтальными полосами, если имеется материя 9 цветов, равно
| 1. | 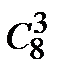
| 2. | 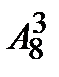
| 3. | 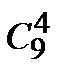
| 4. | 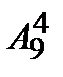
|
ВАРИАНТ 5
1. Множество, не содержащее ни одного элемента, называется
| 1. | простым | 2. | составным | 3. | конечным | 4. | пустым |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
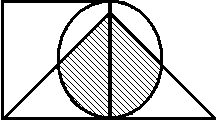
| 1. | 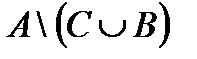
| 3. | 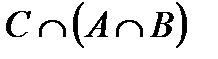
|
| 2. | 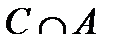
| 4. | 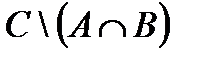
|
3. Поставьте знак отношения, в котором находятся указанные элементы и множества
2, 3 ___ {{2},{3}}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,8}, yÎ{1,...,9}
| x | 8 | 5 | 3 | 6 | 4 | 1 | 3 | 2 | 8 | 7 |
| y | 2 | 5 | 7 | 4 | 6 | 9 | 7 | 8 | 2 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения концентричность на множестве окружностей (концентричными называются окружности, имеющие общий центр) (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 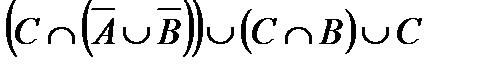
| 1. | 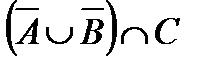
| 2. | С | 3. | 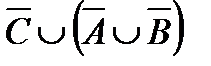
| 4. | Æ |
7. Мощность множества АDА, если А = {x: xÎN и 2 < x < 9}, равна
| 1. | 3 | 2. | 5 | 3. | 7 | 4. | 0 |
8. Найти биективное отображение 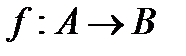 , если
, если 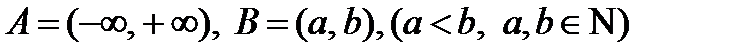
(  )
)
| 1. | y = 0,5(a – b) + (b – a)arctg(x)/p | 3. | y = 0,5(a + b) + (b + a)arctg(x)/p |
| 2. | y = 0,5(a + b) + (b – a)arctg(x)/p | 4. | y = 0,5(a – b) + (b + a)arctg(x)/p |
9. Число размещений из n элементов по m штук обозначается
| 1. | 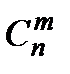
| 2. | 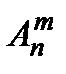
| 3. | 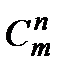
| 4. | 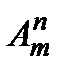
|
10. На полке находятся m + n различных книг, из которых m в черных переплетах, а n – в красных. Количество перестановок книг, при которых книги в черных переплетах занимают первые m мест, равно
| 1. | 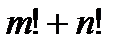
| 2. | 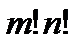
| 3. | 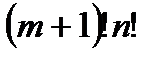
| 4. | 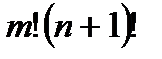
|
ВАРИАНТ 6
1. Множество A называют подмножеством множества B, если
| 1. | всякий элемент множества A является элементом множества B | 3. | всякий элемент множества B является элементом множества A |
| 2. | один элемент множества A является элементом множества B | 4. | ни один элемент множества A не является элементом множества B |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
| 1. | 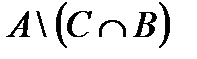
| 3. | 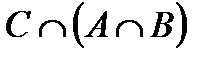
|
| 2. | 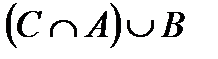
| 4. | 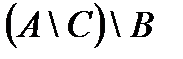
|
3. Если А = {2,3}, то B(А) = {Æ,{2},{3},___} (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 5 | 3 | 6 | 9 | 1 | 9 | 2 | 4 | 8 | 7 |
| y | 6 | 3 | 9 | 6 | 8 | 4 | 2 | 1 | 7 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения иметь непустое пересечение на некотором множестве множеств (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | не транзитивное |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | отношение линейного порядка | 6. | отношение нестрогого частичного порядка |
6. Упростить выражение 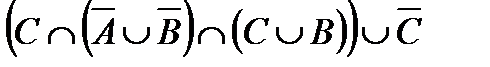
| 1. | 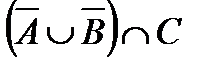
| 2. | С | 3. | 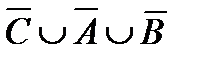
| 4. | Æ |
7. Мощность множества АDÆ, если А = {x: xÎN и 2 < x < 9}, равна
| 1. | 6 | 2. | 5 | 3. | 7 | 4. | 1 |
8. Найти биективное отображение 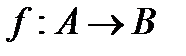 , если
, если 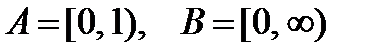 (
(  )
)
| 1. | y = (x – 1)/x | 2. | y = x/(x – 1) | 3. | y = x/(1 + x) | 4. | y = x/(1 – x) |
9. Число сочетаний из n элементов по m штук обозначается
| 1. | 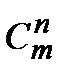
| 2. | 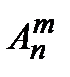
| 3. | 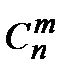
| 4. | 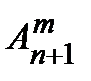
|
10. Есть конверты без марок 8 видов и марки 6 видов. Количество способов, которыми можно выбрать конверт с маркой, равно
| 1. | 48 | 2. | 14 | 3. | 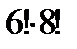
| 4. | 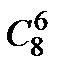
|
ВАРИАНТ 7
1. Два множества А и В называют равными, если
| 1. | состоят из похожих элементов | 3. | состоят из одинаковых элементов |
| 2. | один элемент множества A является элементом множества B | 4. | всякий элемент множества A является элементом множества B |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.

| 1. | 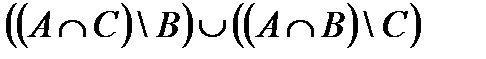
| 3. | 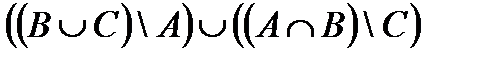
|
| 2. | 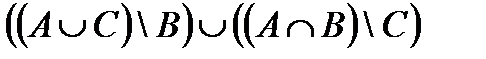
| 4. | 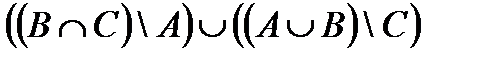
|
3. Если А = {1, 5}, то B(А) = {__,{1},{5},{1, 5}} (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 8 | 1 | 3 | 2 | 4 | 5 | 1 | 6 | 9 | 7 |
| y | 7 | 8 | 2 | 3 | 1 | 6 | 8 | 5 | 4 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения иметь пустое пересечение на некотором множестве множеств (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | не транзитивное |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | отношение эквивалентности | 6. | антирефлексивное |
6. Упростить выражение 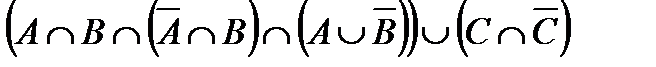
| 1. | Æ | 2. | С | 3. | 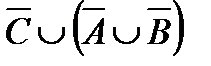
| 4. | 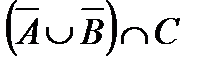
|
7. Мощность множества 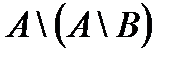 , если А = {x: xÎN и 2 < x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и 2 < x < 9} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 6 | 2. | 5 | 3. | 3 | 4. | 0 |
8. Найти биективное отображение 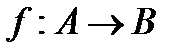 , если
, если 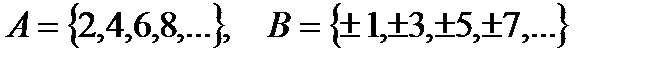
(  )
)
| 1. | |A| = |B|, 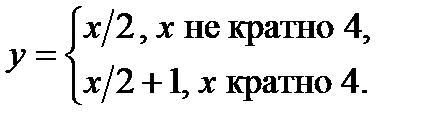
| 3. | |A| = |B|, y = |x| – 1 |
| 2. | |A| = |B|, 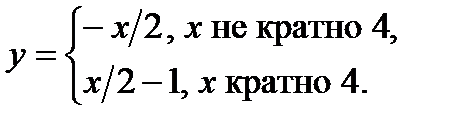
| 4. | |A| = |B|, |y| = x + 1 |
9. Число перестановок из n элементов вычисляется по формуле
| 1. | 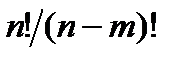
| 2. | 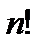
| 3. | 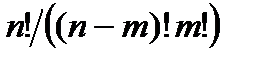
| 4. | 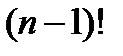
|
10. Из 15 слов мужского рода, 8 женского и 10 среднего нужно выбрать по одному слову каждого рода. Количество способов, которыми можно сделать этот выбор, равно
| 1. | 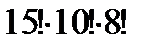
| 2. | 33 | 3. | 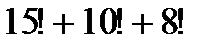
| 4. | 1200 |
ВАРИАНТ 8
1. Множество A называют собственным подмножеством множества B, если
| 1. | AÍB и A = B | 2. | AÍB и A ¹ B | 3. | AÌB и A > B | 4. | AÌB и A = B |
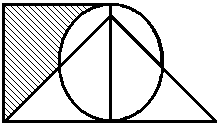 2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
| 1. | 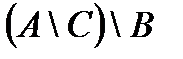
| 3. | 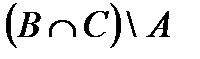
|
| 2. | 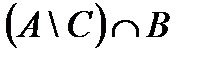
| 4. | 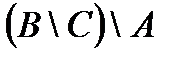
|
3. Согласно закону де Моргана 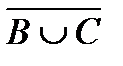 = __________.(ВПИШИТЕ НУЖНОЕ)
= __________.(ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 9 | 1 | 8 | 3 | 2 | 4 | 6 | 9 | 5 | 7 |
| y | 4 | 8 | 7 | 2 | 3 | 1 | 9 | 4 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть выше на некотором множестве людей
(не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 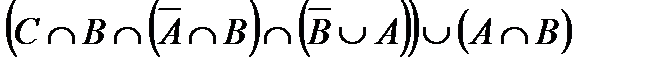
| 1. | Æ | 3. | 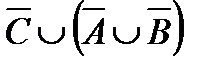
|
| 2. | С | 4. | 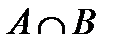
|
7. Мощность множества 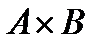 , если А = {x: xÎN и 6 < x < 9} и B = {x: xÎN и (x + 1)2 < 10}, равна
, если А = {x: xÎN и 6 < x < 9} и B = {x: xÎN и (x + 1)2 < 10}, равна
| 1. | 3 | 2. | 5 | 3. | 1 | 4. | 4 |
8. Найти биективное отображение 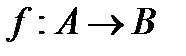 , если
, если 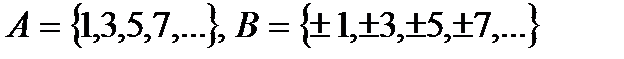
(  )
)
| 1. | |A| = |B|, 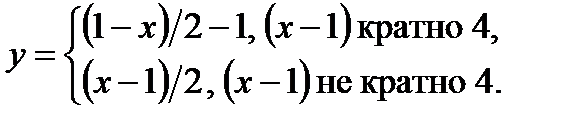
| 3. | |A| = |B|, y = ±|x| |
| 2. | |A| = |B|, 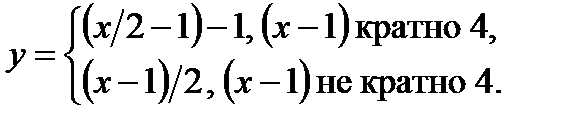
| 4. | |A| = |B|, y = |x| |
9. Число размещений из n элементов по m штук вычисляется по формуле
| 1. | 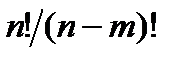
| 2. | 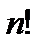
| 3. | 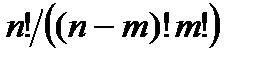
| 4. | 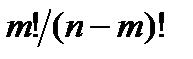
|
10. Количество способов, которыми можно выбрать на шахматной доске белую и черную клетки, не лежащие на одной горизонтали или вертикали, равно
| 1. | 768 | 2. | 56 | 3. | 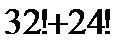
| 4. | 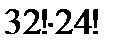
|
ВАРИАНТ 9
1. Обозначение отношения включения между множествами
| 1. | ¹ | 2. | Î | 3. | = | 4. | Í |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
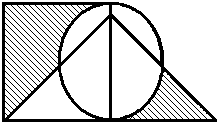
| 1. | 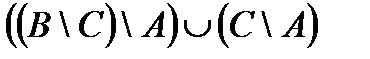
| 3. | 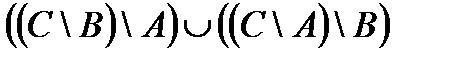
|
| 2. | 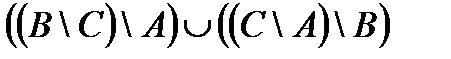
| 4. | 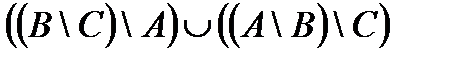
|
3. Согласно закону де Моргана 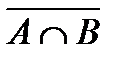 = __________.(ВПИШИТЕ НУЖНОЕ)
= __________.(ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,8}, yÎ{1,...,9}
| x | 7 | 5 | 3 | 6 | 4 | 1 | 3 | 2 | 8 | 7 |
| y | 3 | 5 | 7 | 4 | 6 | 9 | 7 | 8 | 2 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть не ниже на некотором множестве людей
(не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 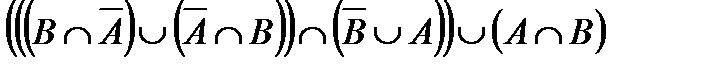
| 1. | Æ | 2. | 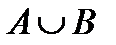
| 3. | 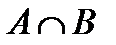
| 4. | 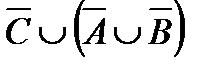
|
7. Мощность множества 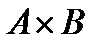 , если А = {x: xÎN и x < 5} и B = {x: xÎN и (x + 1)3 < 28}, равна
, если А = {x: xÎN и x < 5} и B = {x: xÎN и (x + 1)3 < 28}, равна
| 1. | 3 | 2. | 8 | 3. | 1 | 4. | 4 |
8. Найти биективное отображение 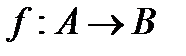 , если
, если 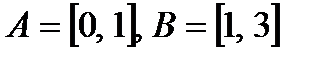 (
(  )
)
| 1. | |A| = |B|, y = x + 1 | 3. | |A| = |B|, y = 2x + 1 |
| 2. | |A| = |B|, y = x + 2 | 4. | |A| = |B|, y = 2x – 1 |
9. Число сочетаний из n элементов по m штук вычисляется по формуле
| 1. | 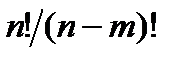
| 2. | 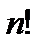
| 3. | 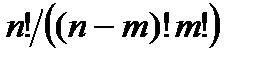
| 4. | 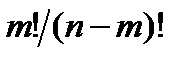
|
10. Замок в автоматической камере хранения содержит 5 дисков, на каждом из которых записаны цифры 0,1,…,9. Количество различных кодов, которые можно получить, равно
| 1. | 100000 | 2. | 10! | 3. | 50 | 4. | 5! |
ВАРИАНТ 10
1. Обозначение отношения принадлежности элемента множеству
| 1. | ¹ | 2. | Î | 3. | = | 4. | Í |
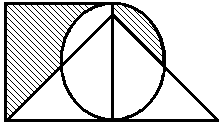 2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
| 1. | 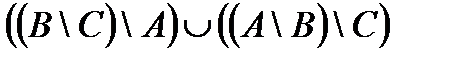
| 3. | 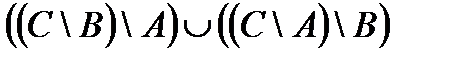
|
| 2. | 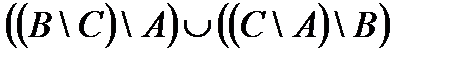
| 4. | 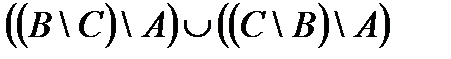
|
3. Согласно закону поглощения AÈ(AÇB) = ________. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 3 | 8 | 1 | 2 | 4 | 5 | 4 | 6 | 9 | 7 |
| y | 2 | 7 | 8 | 3 | 1 | 6 | 1 | 5 | 4 | 6 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения иметь одинаковый цвет на множестве цветных предметов (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | строго антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 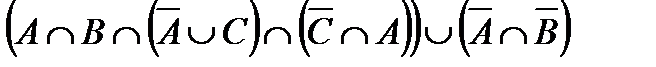
| 1. | Æ | 2. | 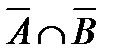
| 3. | 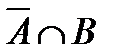
| 4. | 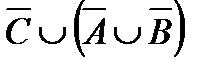
|
7. Мощность множества А ´ Æ, если А = {x: xÎN и 2 < x < 9}, равна
| 1. | 6 | 2. | 5 | 3. | 0 | 4. | 1 |
8. Для множеств 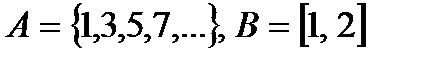 (
(  )
)
| 1. | |A| = |B|, y = 3x – 2 | 2. | |A| < |B| | 3. | |A| > |B| | 4. | |A| = |B|, y = 2x – 1 |
9. Число сочетаний из 6 элементов по 3 вычисляется по формуле
| 1. | 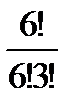
| 2. | 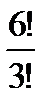
| 3. | 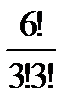
| 4. | 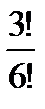
|
10. В группе из 30 человек разыгрывается 4 различных приза. Призы могут достаться одному человеку, двоим, троим, четверым. Количество способов, которыми призы могут распределиться, равно
| 1. | 30 | 2. | 30! | 3. | 304 | 4. | 120 |
ВАРИАНТ 11
1. Обозначение множества, не содержащего элементов
| 1. | Æ | 2. | Î | 3. | ∞ | 4. | ¤ |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
| 1. | 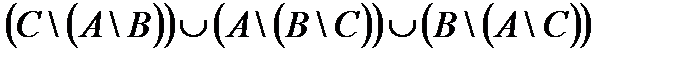
|
| 2. | 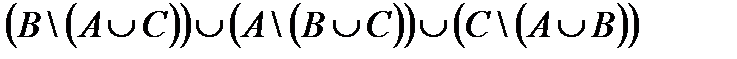
|
| 3. | 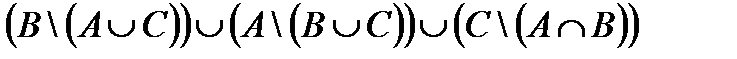
|
| 4. | 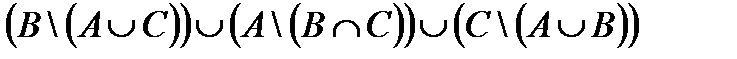
|
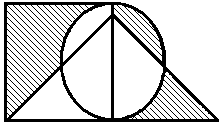
3. Согласно закону поглощения AÇ(AÈB) =________. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 5 | 3 | 6 | 3 | 2 | 4 | 8 | 5 | 9 | 7 |
| y | 8 | 3 | 9 | 2 | 2 | 1 | 7 | 6 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения иметь разный цвет на множестве цветных предметов (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 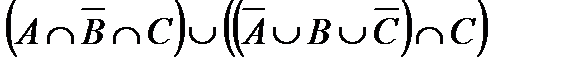
| 1. | С | 3. | 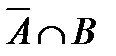
|
| 2. | 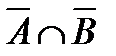
| 4. | 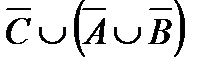
|
7. Мощность множества 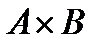 , если А = {x: xÎN и (x – 3)0,5 < 2} и B={x: xÎN и (x + 1)3 < 28}, равна
, если А = {x: xÎN и (x – 3)0,5 < 2} и B={x: xÎN и (x + 1)3 < 28}, равна
| 1. | 8 | 2. | 6 | 3. | 3 | 4. | 9 |
8. Найти биективное отображение 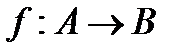 , если
, если 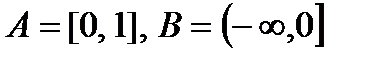 (
(  )
)
| 1. | y = (x – 1)/x | 2. | y = x/(x – 1) | 3. | y = x/(1 + x) | 4. | y = (1 – x)/x |
9. Количество способов, которыми можно выбрать из колоды в 36 карт по одной карте каждой масти, равно
| 1. | 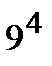
| 2. | 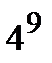
| 3. | 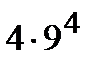
| 4. | 36 |
10. Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Количество способов, которыми можно выбрать эту команду так, чтобы в нее вошло не более двух юношей, равно
| 1. | 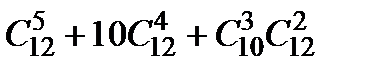
| 3. | 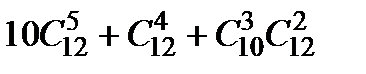
|
| 2. | 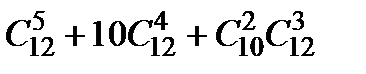
| 4. | 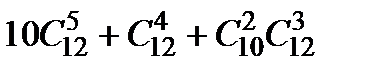
|
ВАРИАНТ 12
1. Множество, элементами которого являются все возможные подмножества данного множества A
| 1. | универсум | 2. | якобиан | 3. | сеть | 4. | Булеан |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
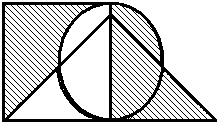
| 1. | 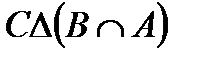
| 3. | 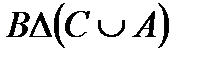
|
| 2. | 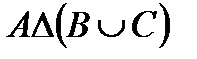
| 4. | 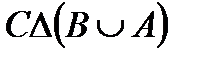
|
3. Согласно свойству дистрибутивности объединения относительно пересечения
AÈ(BÇC) =_________. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 3 | 7 | 1 | 8 | 2 | 4 | 6 | 9 | 5 | 7 |
| y | 2 | 5 | 8 | 7 | 3 | 1 | 9 | 4 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения считать другом кого-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 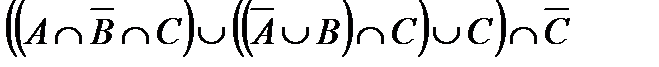
| 1. | С | 2. | 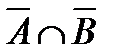
| 3. | 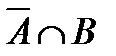
| 4. | Æ |
7. Мощность множества 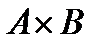 , если А = {x: xÎN и (x – 1)0,5 < 2} и B = {x: xÎN и (x2 + 1)3 < 126}, равна
, если А = {x: xÎN и (x – 1)0,5 < 2} и B = {x: xÎN и (x2 + 1)3 < 126}, равна
| 1. | 4 | 2. | 6 | 3. | 8 | 4. | 9 |
8. Для множеств 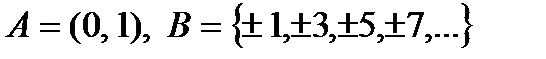 (
(  )
)
| 1. | |A| = |B|, y = 2|x| – 1 | 2. | |A| < |B| | 3. | |A| > |B| | 4. | |A| = |B|, y = 2x – 1 |
9. У одного человека есть 9 книг, у другого – 12. Количество способов, которыми они могут обменять три книги одного на три книги другого, равно
| 1. | 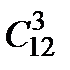
| 2. | 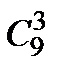
| 3. | 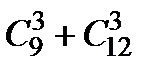
| 4. | 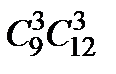
|
10. Из 14 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Количество способов, которыми можно выбрать эту команду так, чтобы в нее вошло не более двух девушек, равно
| 1. | 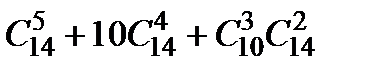
| 3. | 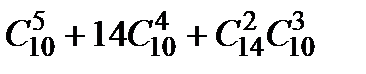
|
| 2. | 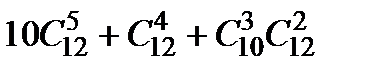
| 4. | 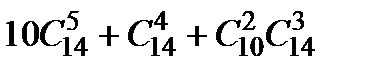
|
ВАРИАНТ 13
1. Если A состоит из 2n элементов, B(A) состоит из
| 1. | 2n | 2. | 23n | 3. | 4n | 4. | 2n |
 2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
| 1. | 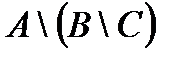
| 3. | 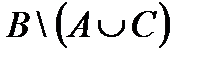
|
| 2. | 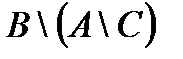
| 4. | 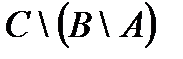
|
3. Согласно свойству дистрибутивности пересечения относительно объединения
AÇ(BÈC) = ____________________. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 8 | 2 | 4 | 3 | 5 | 1 | 6 | 9 | 5 | 7 |
| y | 7 | 3 | 1 | 2 | 6 | 8 | 9 | 4 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения считать врагом кого-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | не симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 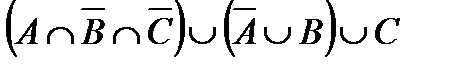
| 1. | С | 2. | 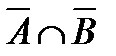
| 3. | U | 4. | Æ |
7. Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42 человека, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Количество студентов, занимающихся только спортом, равно
| 1. | 24 | 2. | 30 | 3. | 20 | 4. | 13 |
8. Для множеств 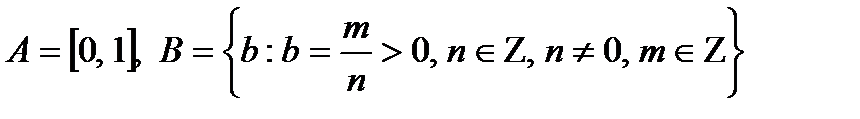 , верно, что
, верно, что
| 1. | |A| = |B| | 2. | |A| > |B| | 3. | |A| < |B| | 4. | A и B не сравнимы |
9. 6 девушек и 4 юношей разбивается на две команды по 5 человек. Количество способов, которыми это можно сделать, равно
| 1. | 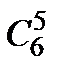
| 3. | 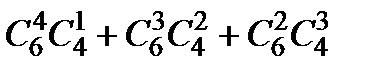
|
| 2. | 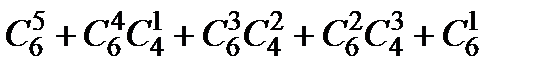
| 4. | 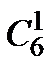
|
10. 10 человек садятся за круглый стол. Два размещения по местам будем считать совпадающими, если каждый человек имеет одних и тех же соседей в обоих случаях. Количество различных способов, которыми можно сесть за стол, равно
| 1. | 9!/2 | 2. | 10!/2 | 3. | 10! | 4. | 9! |
ВАРИАНТ 14
1. Множество всех возможных элементов
| 1. | Булеан | 2. | универсум | 3. | сеть | 4. | якобиан |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
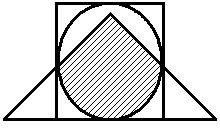
| 1. | 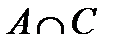
| 3. | 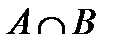
|
| 2. | 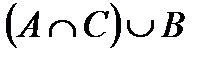
| 4. | 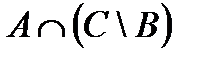
|
3. Согласно свойствам действий над множествами AÈÆ =_____. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{0,...,9}
| x | 7 | 6 | 4 | 1 | 5 | 3 | 9 | 2 | 8 | 7 |
| y | 3 | 4 | 6 | 9 | 5 | 7 | 1 | 8 | 2 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть начальником на некотором множестве людей (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | строго антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 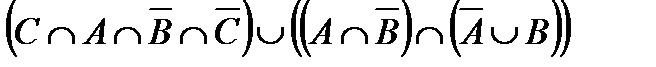
| 1. | С | 2. | 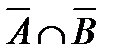
| 3. | U | 4. | Æ |
7. Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42 человека, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Количество студентов, занимающихся только музыкой, равно
| 1. | 24 | 2. | 30 | 3. | 20 | 4. | 14 |
8. Для множеств 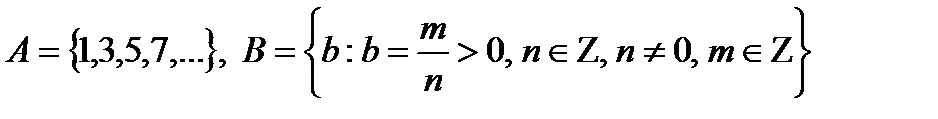 верно
верно
| 1. | |A| = |B| | 2. | |A| > |B| | 3. | |A| < |B| | 4. | A и B не сравнимы |
9. Количество различных буквосочетаний, которое можно получить, переставляя буквы в слове «математика», равно
| 1. | 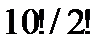
| 2. | 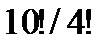
| 3. | 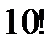
| 4. | 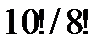
|
10. Из колоды, содержащей 52 карты, вынули 10 карт. Количество случаев, когда среди этих карт окажется хотя бы один туз, равно
| 1. | 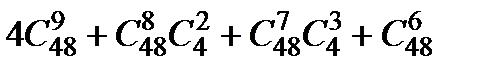
| 3. | 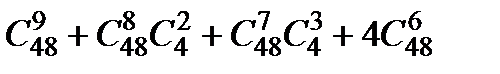
|
| 2. | 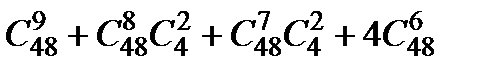
| 4. | 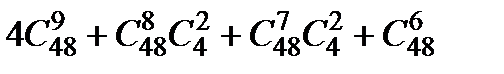
|
ВАРИАНТ 15
1. Операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество
| 1. | объединение | 3. | симметрическая разность |
| 2. | абсолютное дополнение | 4. | относительное дополнение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
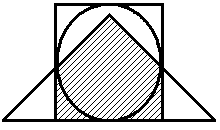
| 1. | 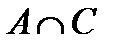
| 3. | 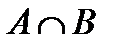
|
| 2. | 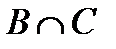
| 4. | 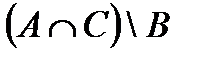
|
3. Согласно свойствам действий над множествами AÈ 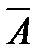 =_____. (ВПИШИТЕ НУЖНОЕ)
=_____. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 3 | 8 | 1 | 2 | 4 | 5 | 8 | 6 | 9 | 7 |
| y | 2 | 7 | 8 | 3 | 1 | 6 | 7 | 7 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть знакомым с кем-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | не симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 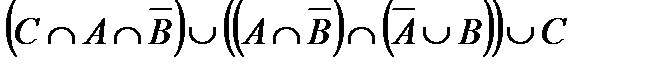
| 1. | С | 2. | 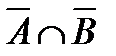
| 3. | U | 4. | Æ |
7. Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42 человека, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Количество студентов, занимающихся только живописью, равно
| 1. | 7 | 2. | 20 | 3. | 22 | 4. | 13 |
8. Для множеств 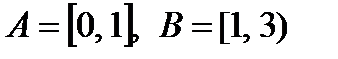 (
(  ) справедливо
) справедливо
| 1. | |A| > |B| | 2. | |A| = |B| | 3. | |A| < |B| | 4. | |A| = |B|, y = 2x + 1 |
9. Из спортивного клуба, насчитывающего 40 членов, надо составить команду из 6 человек для участия в забеге на 100 м. Количество способов, которым это можно сделать, равно
| 1. | 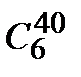
| 2. | 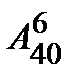
| 3. | 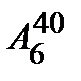
| 4. | 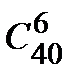
|
10. Из колоды, содержащей 36 карт, вынули 5. Количество случаев, в которых среди этих карт окажется хотя бы одна дама красной масти, равно
| 1. | 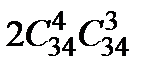
| 2. | 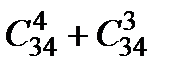
| 3. | 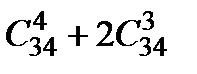
| 4. | 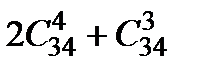
|
ВАРИАНТ 16
1. Операция, результатом которой является множество элементов этих множеств, принадлежащих одному и только одному из них
| 1. | объединение | 3. | симметрическая разность |
| 2. | абсолютное дополнение | 4. | относительное дополнение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
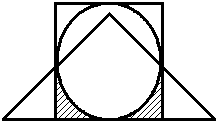
| 1. | 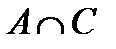
| 3. | 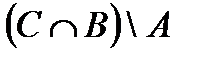
|
| 2. | 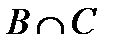
| 4. | 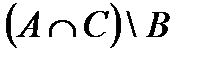
|
3. Согласно свойствам действий над множествами AÈA =____. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 4 | 2 | 6 | 1 | 8 | 5 | 3 | 7 | 9 | 7 |
| y | 2 | 2 | 1 | 8 | 7 | 6 | 3 | 9 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть незнакомым с кем-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | строго антисимметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 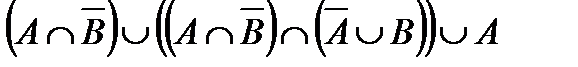
| 1. | С | 2. | A | 3. | U | 4. | Æ |
7. Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42 человека, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Количество студентов, не увлекающихся ничем, равно
| 1. | 16 | 2. | 20 | 3. | 0 | 4. | 26 |
8. Найти биективное отображение 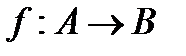 , (
, (  ) если
) если
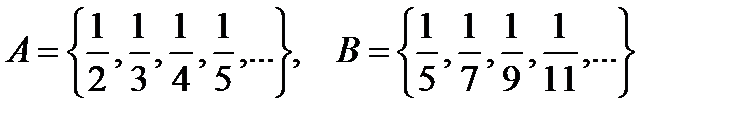 .
.
| 1. | y = (x – 2)/x | 2. | y = x/(x – 2) | 3. | y = (2 + x)/x | 4. | y = x/(2 + x) |
9. Имеется 20 абонентов телефонной сети. Количество способов, которыми можно одновременно соединить три пары абонентов, равно
| 1. | 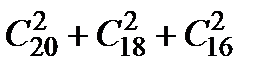
| 2. | 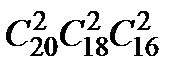
| 3. | 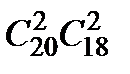
| 4. | 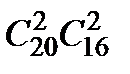
|
10. Количество способов, которыми можно составить три пары из 30 шахматистов, равно
| 1. | 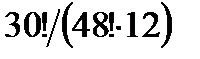
| 2. | 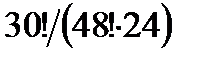
| 3. | 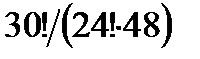
| 4. | 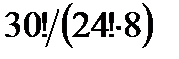
|
ВАРИАНТ 17
1. Операция, результатом которой является множество, которому одновременно принадлежат элементы всех данных множеств
| 1. | пересечение | 3. | объединение |
| 2. | абсолютное дополнение | 4. | относительное дополнение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
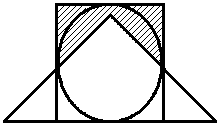
| 1. | 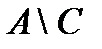
| 3. | 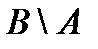
|
| 2. | 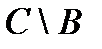
| 4. | 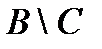
|
3. Согласно свойствам действий над множествами AÈU =____ (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 4 | 8 | 2 | 3 | 5 | 1 | 6 | 9 | 4 | 7 |
| y | 1 | 7 | 3 | 2 | 6 | 8 | 9 | 4 | 1 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть кратным на множестве натуральных чисел (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение эквивалентности |
| 2. | антисимметричное | 5. | отношение нестрогого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 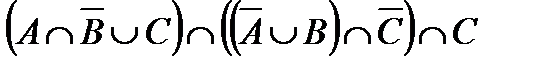
| 1. | С | 2. | A | 3. | U | 4. | Æ |
7. Известно, что из 80 студентов юношей шатенов 28 человек, голубоглазых – 22, выше 170 см. – 30, шатенов и голубоглазых – 8, шатенов и выше 170 см.– 15, голубоглазых и выше 170 см. – 9, шатенов, голубоглазых и выше 170 см. – 5. Количество студентов юношей шатенов, не голубоглазых и не выше 170 см, равно
| 1. | 15 | 2. | 8 | 3. | 0 | 4. | 10 |
8. Найти биективное отображение 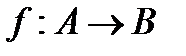 , (
, (  ) если
) если
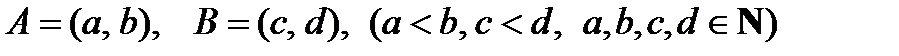 .
.
| 1. | y = c – (d – c)(x – a)/(b – a) | 3. | y= c + (d – c)(x – a)/(b – a) |
| 2. | y = c + (d – c)(x + a)/(b – a) | 4. | y= c + (d + c)(x – a)/(b – a) |
9. Количество способов, которыми могут встать в круг 8 юношей и 8 девушек, равно
| 1. | 15! | 2. | 16! | 3. | 8!+8! | 4. | 8!8! |
10. Количество чисел от 0 до 1000, в которые не входят две идущие друг за другом одинаковые цифры, равно
| 1. | 920 | 2. | 821 | 3. | 810 | 4. | 910 |
ВАРИАНТ 18
1. Операция, результатом которой является множество, содержащее в себе все элементы исходных множеств
| 1. | пересечение | 3. | объединение |
| 2. | абсолютное дополнение | 4. | относительное дополнение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.

| 1. | 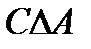
| 3. | 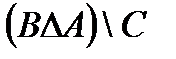
|
| 2. | 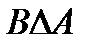
| 4. | 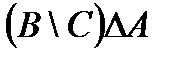
|
3. Согласно свойствам действий над множествами AÇÆ =____. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{0,...,9}
| x | 2 | 4 | 8 | 5 | 3 | 6 | 9 | 1 | 2 | 7 |
| y | 2 | 4 | 8 | 5 | 3 | 6 | 9 | 1 | 2 | 7 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения включение 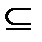 на некотором множестве множеств (не менее двух правильных ответов).
на некотором множестве множеств (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение эквивалентности |
| 2. | антисимметричное | 5. | отношение нестрогого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 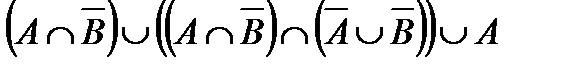
| 1. | С | 2. | A | 3. | U | 4. | Æ |
7. Известно, что из 80 студентов юношей шатенов 28 человек, голубоглазых – 22, выше 170 см. – 30, шатенов и голубоглазых – 8, шатенов и выше 170 см.– 15, голубоглазых и выше 170 см. – 9, шатенов, голубоглазых и выше 170 см. – 5. Найти количество студентов голубоглазых юношей не шатенов и не выше 170 см.
| 1. | 10 | 2. | 8 | 3. | 0 | 4. | 9 |
8. Найти биективное отображение 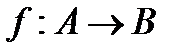 , если
, если 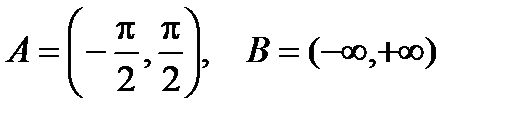 (
(  )
)
| 1. | y= tgx | 2. | y= сtgx | 3. | y= – ctgx | 4. | y= – tgx |
9. Количество способов, которыми могут встать в круг 8 юношей и 8 девушек,
если необходимо, чтобы никакие двое юношей или девушек не стояли рядом, равно
| 1. | 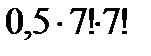
| 2. | 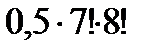
| 3. | 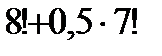
| 4. | 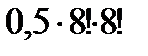
|
10. Из 28 костей домино берутся 2. Количество комбинаций, когда вторая кость будет приставляема к первой, равно
| 1. | 756 | 2. | 42 | 3. | 294 | 4. | 252 |
ВАРИАНТ 19
1. Операция, результатом которой является множество всех элементов, не принадлежащих данному множеству A
| 1. | пересечение | 3. | объединение |
| 2. | абсолютное дополнение | 4. | относительное дополнение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
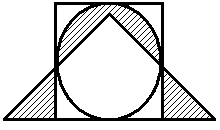
| 1. | 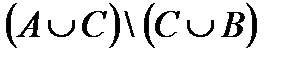
| 3. | 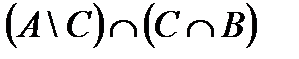
|
| 2. | 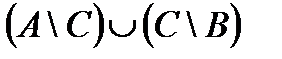
| 4. | 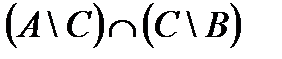
|
3. Согласно свойствам действий над множествами AÇA =___. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 4 | 8 | 2 | 1 | 3 | 5 | 1 | 6 | 9 | 7 |
| y | 1 | 7 | 3 | 8 | 2 | 6 | 8 | 9 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть не меньше на множестве натуральных чисел (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение эквивалентности |
| 2. | антисимметричное | 5. | отношение нестрогого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 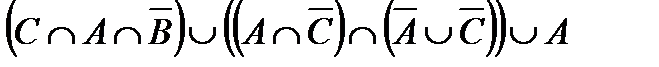
| 1. | С | 2. | Æ | 3. | U | 4. | A |
7. Известно, что из 80 студентов юношей шатенов 28 человек, голубоглазых – 22, выше 170 см. – 30, шатенов и голубоглазых – 8, шатенов и выше 170 см.– 15, голубоглазых и выше 170 см. – 9, шатенов, голубоглазых и выше 170 см. – 5. Найти количество студентов юношей выше 170 см, не голубоглазых и не шатенов.
| 1. | 0 | 2. | 8 | 3. | 11 | 4. | 9 |
8. Найти биективное отображение 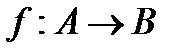 , если
, если 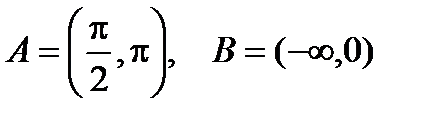 (
(  )
)
| 1. | y= tgx | 2. | y= сtgx | 3. | y= – ctgx | 4. | y= – tgx |
9. Количество различных ожерелий, которые можно составить из 10 различных бусинок, равно
| 1. | 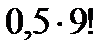
| 2. | 10! | 3. | 11! | 4. | 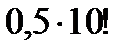
|
10. Найти количество перестановок букв слова «комбинаторика».
| 1. | 16! | 2. | 13! | 3. | 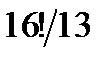
| 4. | 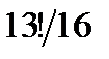
|
ВАРИАНТ 20
1. Совокупность, состоящая из двух элементов x и y, расположенных в определенном порядке
| 1. | упорядоченная пара | 3. | упорядоченный набор |
| 2. | подмножество | 4. | двуместное отношение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
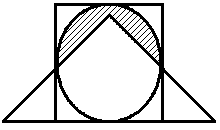
| 1. | 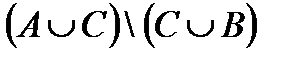
| 3. | 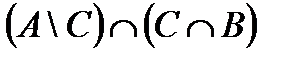
|
| 2. | 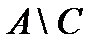
| 4. | 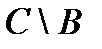
|
3. Согласно свойствам действий над множествами AÇ 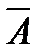 =____. (ВПИШИТЕ НУЖНОЕ)
=____. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{0,...,9}
| x | 1 | 5 | 2 | 4 | 8 | 9 | 3 | 6 | 4 | 7 |
| y | 8 | 4 | 2 | 1 | 7 | 6 | 3 | 9 | 1 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения делимость на множестве целых чисел
(не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | не симметричное | 5. | отношение нестрогого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 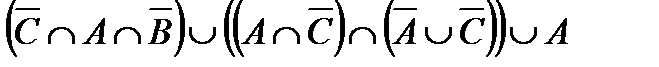
| 1. | С | 2. | Æ | 3. | U | 4. | A |
7. Известно, что из 80 студентов юношей шатенов 28 человек, голубоглазых – 22, выше 170 см. – 30, шатенов и голубоглазых – 8, шатенов и выше 170 см.– 15, голубоглазых и выше 170 см. – 9, шатенов, голубоглазых и выше 170 см. – 5. Найти количество студентов девушек.
| 1. | 53 | 2. | 19 | 3. | 0 | 4. | 27 |
8. Найти биективное отображение 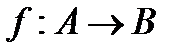 , если
, если 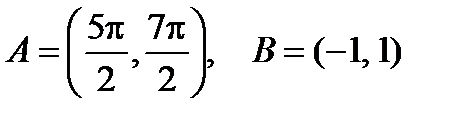 (
(  )
)
| 1. | y= sinx | 2. | y= сosx | 3. | y= – sinx | 4. | y= – cosx |
9. В военной части находятся 7 офицеров, 8 сержантов и 80 рядовых. Количество способов, которыми можно выделить из них отряд, состоящий из офицера, двух сержантов
и 20 рядовых, равно
| 1. | 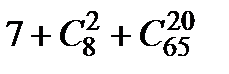
| 2. | 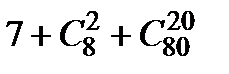
| 3. | 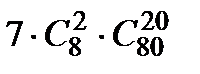
| 4. | 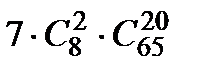
|
10. У ученика 2 одинаковые авторучки, 4 одинаковых карандаша и 1 резинка.
Он раскладывает эти предметы на парте в ряд. Количество вариантов раскладки равно
| 1. | 105 | 2. | 15 | 3. | 7! | 4. | 15! |
ВАРИАНТ 21
1. Множество упорядоченных пар
| 1. | подкласс | 3. | упорядоченный набор |
| 2. | подмножество | 4. | бинарное отношение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
| 1. | 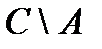
| 3. | 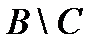
|
| 2. | 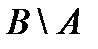
| 4. | 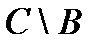
|
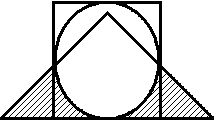
3. Найти область определения и область значений бинарного отношения
{<1, 2>,<2, 4>,<3, 4>,<2, 2>} (ВПИШИТЕ НУЖНОЕ)
Dr = {_______________}, Rr = {_______________}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 6 | 7 | 8 | 4 | 3 | 2 | 1 | 5 | 9 | 2 |
| y | 8 | 2 | 2 | 1 | 7 | 6 | 3 | 9 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения подобие на множестве геометрических фигур
(не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | антисимметричное | 5. | отношение нестрогого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 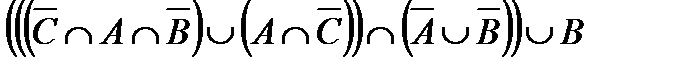
| 1. | С | 2. | Æ | 3. | 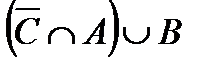
| 4. | A |
7. Мощность множества 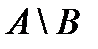 , если А = {x: xÎN и 6 < x < 11} и B = {x: xÎN и (x + 1)2 < 40}, равна
, если А = {x: xÎN и 6 < x < 11} и B = {x: xÎN и (x + 1)2 < 40}, равна
| 1. | 3 | 2. | 5 | 3. | 4 | 4. | 9 |
8. Найти биективное отображение 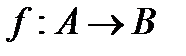 , если
, если 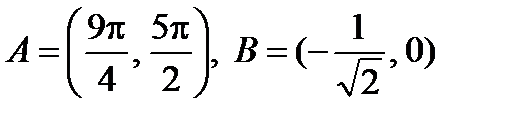 (
(  )
)
| 1. | y= sinx | 2. | y= сosx | 3. | y= – sinx | 4. | y= – cosx |
9. Рота состоит из 3 офицеров, 6 сержантов и 60 рядовых. Количество способов, которыми можно выделить из них отряд, состоящий из офицера, 3 сержантов и 30 рядовых, равно
| 1. | 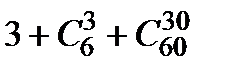
| 2. | 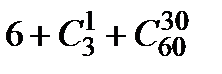
| 3. | 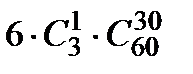
| 4. | 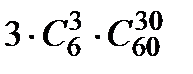
|
10. Из 25 работников надо выбрать председателя, заместителя, бухгалтера и казначея. Количество способов, которыми это можно сделать, равно
| 1. | 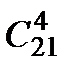
| 2. | 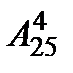
| 3. | 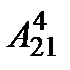
| 4. | 
|
ВАРИАНТ 22
1. Последовательность, состоящая из элементов, расположенных в определенном порядке
| 1. | упорядоченная пара | 3. | упорядоченный набор |
| 2. | подмножество | 4. | двуместное отношение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
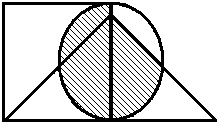
| 1. | 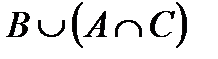
| 3. | 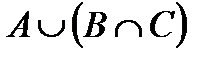
|
| 2. | 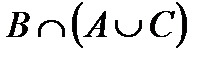
| 4. | 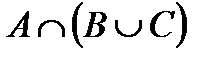
|
3. Найти область определения и область значений бинарного отношения {<5, 2>,<7, 5><3, 3>,<1, 2>} (ВПИШИТЕ НУЖНОЕ)
Dr = {_______________}, Rr = {_______________}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{0,...,9}
| x | 8 | 5 | 3 | 6 | 3 | 4 | 9 | 1 | 2 | 7 |
| y | 8 | 5 | 3 | 6 | 3 | 4 | 9 | 1 | 2 | 7 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения равенство на множестве натуральных чисел (не менее двух правильных ответов).
| 1. | не рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение нестрогого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 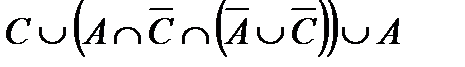
| 1. | С | 2. | 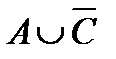
| 3. | A | 4. | 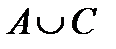
|
7. Даны множества А = {1,2,3,4,5}, В = {3,6,7,8}, С = {1,7,9,10,11} Мощность множества 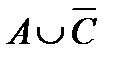 равна
равна
| 1. | 7 | 2. | 5 | 3. | 3 | 4. | 9 |
8. Найти биективное отображение 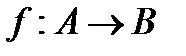 , если
, если 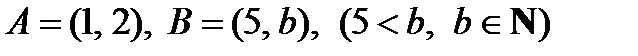
(  )
)
| 1. | y = (5 – b)x + 10 – b | 3. | y = (b + 5)x – 10 – b |
| 2. | y = (b – 5)x + 10 – b | 4. | y = (5 – b)x + 10 + b |
9. У ювелира есть 10 одинаковых изумрудов, 8 одинаковых рубинов и 6 одинаковых сапфиров. Количество способов, которыми он может выбрать из них три камня для брошки, равно
| 1. | 9 | 2. | 10 | 3. | 11 | 4. | 8 |
10. Рыбаки поймали 5 окуней, 4 щуки и 2 подлещика, посолили и вывесили на солнце сушиться. Количество вариантов развешивания рыбы на нитке равно
| 1. | 11! | 2. | 6930 | 3. | 37! | 4. | 37 |
ВАРИАНТ 23
1. Множество, элементами которого являются все возможные упорядоченные наборы элементов исходных n множеств
| 1. | прямое произведение | 3. | упорядоченный набор |
| 2. | произведение | 4. | двуместное отношение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
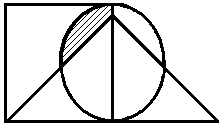
| 1. | 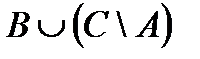
| 3. | 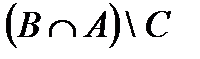
|
| 2. | 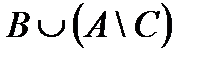
| 4. | 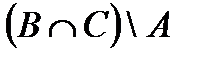
|
3. Пусть X={0, 1}, Y={x, y}. Тогда (ВПИШИТЕ НУЖНОЕ):
X ´ Y = {<0, x>, <0, y>, _____, <1, y>}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 4 | 8 | 1 | 3 | 2 | 5 | 3 | 6 | 9 | 7 |
| y | 1 | 7 | 8 | 2 | 3 | 6 | 2 | 9 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения нравиться кому-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | не симметричное | 5. | симметричное |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 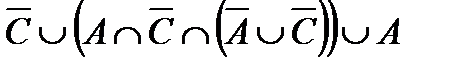
| 1. | 
| 2. | Æ | 3. | A | 4. | 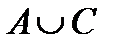
|
7. Даны множества А = {1,2,3,4,5}, В = {3,6,7,8}, С = {1,7,9,10,11} Мощность множества 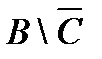 равна
равна
| 1. | 4 | 2. | 5 | 3. | 3 | 4. | 1 |
8. Найти биективное отображение 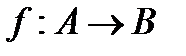 , если
, если 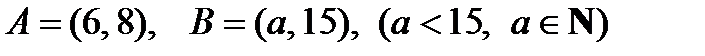
(  )
)
| 1. | y = (15 – a)x/2 + 4a – 45 | 3. | y = (a –15)x/2 + 4a + 45 |
| 2. | y = (a –15)x/2 + 4a – 45 | 4. | y = (15 – a)x/2 – 4a – 45 |
9. Дано m предметов одного сорта и n другого. Найти число выборок, составленных из r предметов одного сорта и s другого.
| 1. | 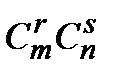
| 2. | 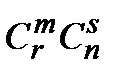
| 3. | 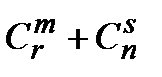
| 4. | 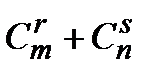
|
10. Количество 7 разрядных чисел, в первых трех разрядах которых нет цифр 0, 8, 9, равно
| 1. | 49000 | 2. | 490000 | 3. | 343000 | 4. | 3430000 |
ВАРИАНТ 24
1. Двухместное отношение, состоящее из пар элементов 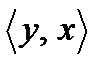 , полученных перестановкой пар элементов
, полученных перестановкой пар элементов 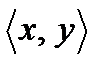 данного отношения r
данного отношения r
| 1. | двуместное отношение | 3. | упорядоченный набор |
| 2. | обратное отношение | 4. | композиция отношений |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
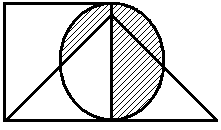
| 1. | 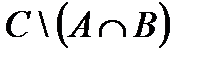
| 3. | 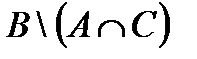
|
| 2. | 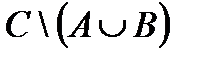
| 4. | 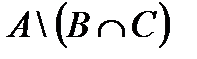
|
3. Пусть X = {1, 2, 4}, Y = {0, 1}. Тогда (ВПИШИТЕ НУЖНОЕ):
X ´ Y = {<1, 0>,<1, 1>,<2, 0>,____,<4, 0>,<4, 1>}.
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 9 | 7 | 3 | 8 | 1 | 2 | 4 | 5 | 3 | 6 |
| y | 4 | 5 | 2 | 7 | 8 | 3 | 1 | 6 | 2 | 4 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения знать кого-либо на некотором множестве людей (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение нестрогого частичного порядка |
| 2. | симметричное | 5. | строго антисимметричное |
| 3. | не транзитивное | 6. | отношение эквивалентности |
6. Упростить выражение 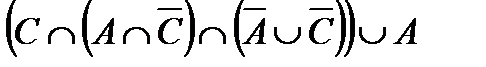
| 1. | С | 2. | Æ | 3. | A | 4. | 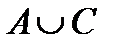
|
7. Даны множества А = {1,2,3,4,5}, В = {3,6,7,8}, С = {1,7,9,10,11} Мощность множества 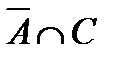 равна
равна
| 1. | 5 | 2. | 4 | 3. | 3 | 4. | 0 |
8. Найти биективное отображение 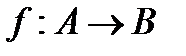 , если
, если 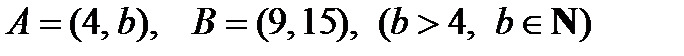
(  )
)
| 1. | y = (6x – 9b + 60)/(4– b) | 3. | y = (6x + 9b – 60)/(b – 4) |
| 2. | y = (6x + 9b – 60)/(4 – b) | 4. | y = (6x – 9b + 60)/(b – 4) |
9. Дано m предметов одного сорта и n другого. Найти число перестановок в выборке, составленной из r предметов одного сорта и s другого.
| 1. | (n + m)! | 2. | (rs)! | 3. | (r + s)! | 4. | (nm)! |
10. Количество автомобильных номеров, содержащих 3 буквы из 20 и 5 цифр из 10, равно
| 1. | 203+105 | 2. | 205·103 | 3. | 203·105 | 4. | 205+103 |
ВАРИАНТ 25
1. Функция f: A → B (где A – область определения отношения, B – область значений отношения)
| 1. | двуместное отношение | 3. | упорядоченный набор |
| 2. | обратное отношение | 4. | отображение |
2. Построить выражение над множествами A (круг), B (квадрат) и C (треугольник), которому соответствуют заштрихованные области на приведенной диаграмме Эйлера–Венна.
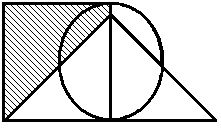
| 1. | 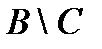
| 3. | 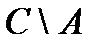
|
| 2. | 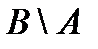
| 4. | 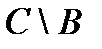
|
3. Если  ,
, 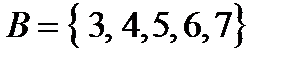 , то объединением множеств А и В будет{_______________}. (ВПИШИТЕ НУЖНОЕ)
, то объединением множеств А и В будет{_______________}. (ВПИШИТЕ НУЖНОЕ)
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{0,...,9}
| x | 1 | 5 | 2 | 4 | 8 | 9 | 3 | 6 | 9 | 7 |
| y | 8 | 4 | 2 | 1 | 7 | 6 | 3 | 9 | 6 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть супругами на некотором множестве людей (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение строгого частичного порядка |
| 2. | симметричное | 5. | не симметричное |
| 3. | отношение эквивалентности | 6. | отношение нестрогого частичного порядка |
6. Упростить выражение 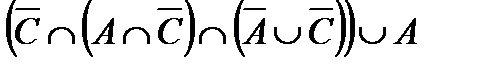
| 1. | С | 2. | 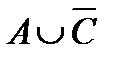
| 3. | A | 4. | 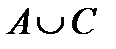
|
7. Даны множества А = {1,2,3,4,5}, В = {3,6,7,8}, С = {1,7,9,10,11} Мощность множества 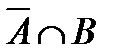 равна
равна
| 1. | 5 | 2. | 4 | 3. | 3 | 4. | 0 |
8. Найти биективное отображение 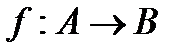 , если
, если 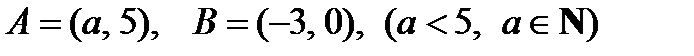
(  )
)
| 1. | y = (3x – 15)/(5 – a) | 3. | y = (3x – 15)/(a – 5) |
| 2. | y = (x – 5)/(5 – a) | 4. | y = (x – 5)/(a – 5) |
9. Количество способов, которыми можно выбрать 12 человек из 17, если данные 2 человека не могут быть выбраны вместе, равно
| 1. | 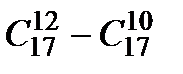
| 2. | 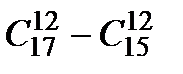
| 3. | 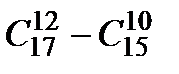
| 4. | 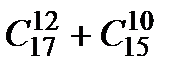
|
10. Количество 5 разрядных чисел, в последних трех разрядах которых нет цифр 0, 8, 9, равно
| 1. | 30870 | 2. | 34300 | 3. | 40 | 4. | 41 |
ВАРИАНТ 26
1. Отношение равномощности множеств является отношением
| 1. | линейного порядка | 3. | нестрогого частичного порядка |
| 2. | строгого частичного порядка | 4. | эквивалентности |
2. Построить выражение над множеством A (круг), которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
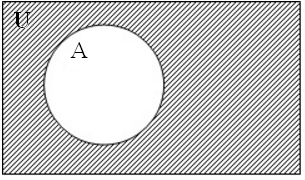
| 1. | 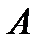
| 3. | 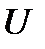
|
| 2. | 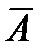
| 4. | 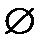
|
3. Дополнением бинарного отношения r между элементами А и В называется множество_____________ (ВПИШИТЕ НУЖНУЮ ФОРМУЛУ).
4. Даны пары <x, y>Îr, причем xÎ{1,...,9}, yÎ{1,...,8}
| x | 1 | 3 | 2 | 4 | 8 | 5 | 3 | 6 | 9 | 7 |
| y | 8 | 6 | 7 | 5 | 1 | 4 | 6 | 3 | 6 | 2 |
Приведенное бинарное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения равносильности на множестве выражений теории множеств (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | антисимметричное |
| 2. | не симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 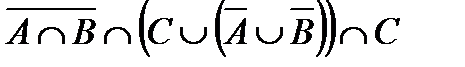
| 1. | 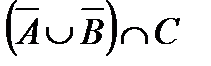
| 3. | 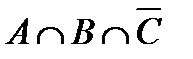
|
| 2. | 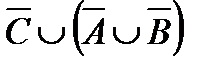
| 4. | Æ |
7. Мощность множества 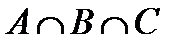 , если А = {x: xÎN и x < 8}, B={x: xÎN и (x + 1)2 < 36}
, если А = {x: xÎN и x < 8}, B={x: xÎN и (x + 1)2 < 36}
и С = {x: xÎZ и |x + 2| < 3}, равна
| 1. | 16 | 2. | 0 | 3. | 12 | 4. | 8 |
8. Найти биективное отображение 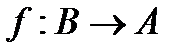 , если
, если 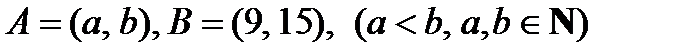
( 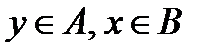 )
)
| 1. | y = (x(b – 15) – 9b + 15a)/(a – 9) | 3. | y = (x(b – 15) – 9b + 15a)/6 |
| 2. | y = (x(b + a) – 9b + 15a)/6 | 4. | y = (x(b – a) – 9b + 15a)/6 |
9. Число размещений с повторениями объемом m из n элементов вычисляется по формуле
| 1. | 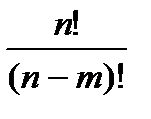
| 2. | 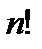
| 3. | 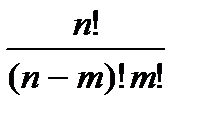
| 4. | 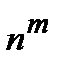
|
10. В шахматном турнире участвует 10 человек и каждый с каждым играет по одной партии. Количество партий, сыгранных в турнире, равно
| 1. | 100 | 2. | 50 | 3. | 90 | 4. | 45 |
ВАРИАНТ 27
1. Множество, равномощное множеству натуральных чисел, называется
| 1. | конечным | 3. | счетным |
| 2. | нет правильного ответа | 4. | континуальным |
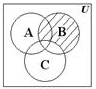 2. Построить выражение над множествами, которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
2. Построить выражение над множествами, которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
| 1. | 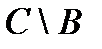
| 3. | 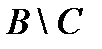
|
| 2. | 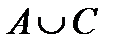
| 4. | 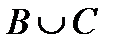
|
3. Обратным отношением для бинарного отношенияr ( 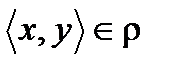 ) называется отношение ____________ (ВПИШИТЕ НУЖНУЮ ФОРМУЛУ).
) называется отношение ____________ (ВПИШИТЕ НУЖНУЮ ФОРМУЛУ).
4. Даны пары <x,y>Îr, причем xÎ{1,...,9}, yÎ{1,...,9}
| x | 4 | 1 | 3 | 2 | 8 | 5 | 3 | 6 | 1 | 7 |
| y | 6 | 9 | 7 | 8 | 2 | 5 | 1 | 4 | 9 | 3 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения достижимости на множестве населенных пунктов некоторого государства (из пункта А достижим пункт В) (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 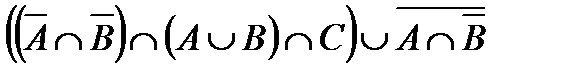
| 1. | 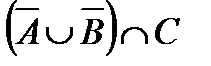
| 3. | Æ |
| 2. | 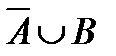
| 4. | С |
7. Мощность множества  , если А = {x: xÎN и x < 8}, B = {x: xÎN и (x + 1)2 < 36}
, если А = {x: xÎN и x < 8}, B = {x: xÎN и (x + 1)2 < 36}
и С={x: xÎZ и |x + 2| < 3}, равна
| 1. | 16 | 2. | 0 | 3. | 12 | 4. | 4 |
8. Найти биективное отображение 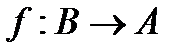 , если
, если 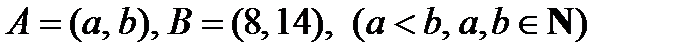
( 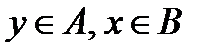 )
)
| 1. | y= (x(b – 14) – 8b + 14a)/(a – 8) | 3. | y= (x(b – a) – 8b + 14a)/6 |
| 2. | y= (x(b + a) – 8b + 14a)/6 | 4. | y= (x(b – 14) – 8b + 14a)/6 |
9. Число сочетаний с повторениями объемом m из n элементов вычисляется по формуле
| 1. | 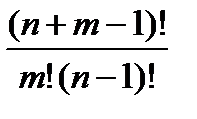
| 2. | 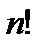
| 3. | 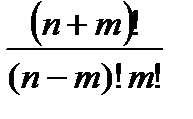
| 4. | 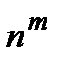
|
10. В отделе работает 8 мужчин и каждый с каждым здоровается за руку. Количество рукопожатий, которые они совершают, равно
| 1. | 64 | 2. | 56 | 3. | 28 | 4. | 32 |
ВАРИАНТ 28
1. Множество, равномощное множеству действительных чисел, называется
| 1. | конечным | 3. | счетным |
| 2. | нет правильного ответа | 4. | континуальным |
2. Построить выражение над множествами, которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
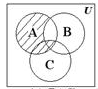
| 1. | 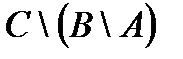
| 3. | 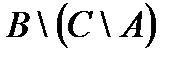
|
| 2. | 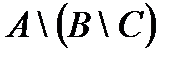
| 4. | 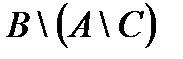
|
3. Рефлексивное и транзитивное бинарное отношение на множестве A называется____________ (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{0,...,9}, yÎ{0,...,8}
| x | 1 | 3 | 2 | 4 | 8 | 5 | 0 | 6 | 9 | 7 |
| y | 8 | 2 | 3 | 1 | 7 | 0 | 6 | 8 | 4 | 5 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения неравенство на множестве натуральных чисел (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | антисимметричное |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | не транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 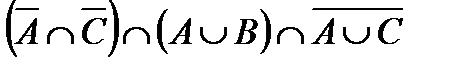
| 1. | 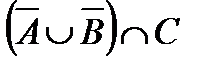
| 2. | 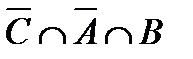
| 3. | Æ | 4. | 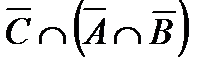
|
7. Мощность множества 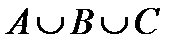 , если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
, если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
и С = {x: xÎZ и |x + 2| < 3}, равна
| 1. | 14 | 2. | 23 | 3. | 12 | 4. | 16 |
8. Найти биективное отображение 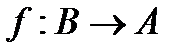 , если
, если 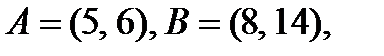 (
( 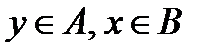 )
)
| 1. | y = (x + 22)/6 | 3. | y = (x – 22)/6 |
| 2. | y = 6x – 22 | 4. | y = 6x – 22 |
9. Число перестановок с повторениями из n элементов, среди которых k1элементов первого типа, k2 элементов второго типа и т. д., ks элементов s-го типа, причем k1 + k2 +...+ ks = n вычисляется по формуле
| 1. | 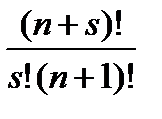
| 2. | 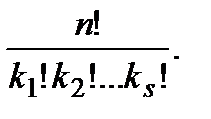
| 3. | 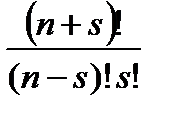
| 4. | 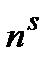
|
10. Количество способов, которыми можно из студенческой группы, состоящей из 9 юношей и 8 девушек, выбрать двух человек одного пола, равно
| 1. | 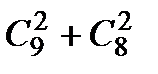
| 2. | 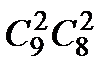
| 3. | 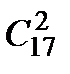
| 4. | 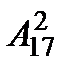
|
ВАРИАНТ 29
1. Найдите самое мощное множество
| 1. | Булеан | 3. | континуальное |
| 2. | нет правильного ответа | 4. | счетное |
2. Построить выражение над множествами, которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
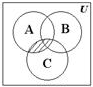
| 1. | 
| 3. | 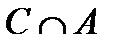
|
| 2. | 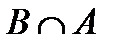
| 4. | 
|
3. Антирефлексивное, строго антисимметричное и транзитивное отношение на множестве A называется отношением____________ (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{0,...,9}, yÎ{0,...,9}
| x | 3 | 8 | 1 | 2 | 4 | 5 | 0 | 6 | 9 | 7 |
| y | 6 | 1 | 8 | 7 | 5 | 4 | 9 | 3 | 0 | 2 |
Приведенное отношение r
| 1. | не является функцией | 3. | является функцией |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения иметь большую мощность на множестве всех множеств (не менее двух правильных ответов).
| 1. | антирефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 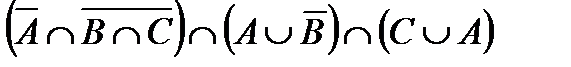
| 1. | 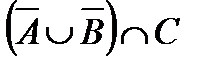
| 2. | 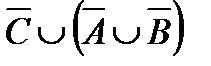
| 3. | 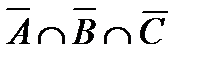
| 4. | 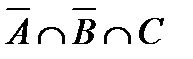
|
7. Мощность множества 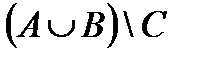 , если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
, если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
и С = {x: xÎZ и |x + 2| < 3}, равна
| 1. | 14 | 2. | 23 | 3. | 9 | 4. | 16 |
8. Найти биективное отображение 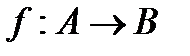 , если
, если 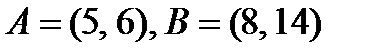 , (
, ( 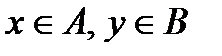 )
)
| 1. | y = (x + 22)/6 | 3. | y = (x – 22)/6 |
| 2. | y = 6x – 22 | 4. | y = 6x + 22 |
9. Число перестановок из 5 элементов равно
| 1. | 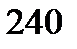
| 2. | 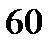
| 3. | 
| 4. | 
|
10. Количество способов, которыми можно из студенческой группы, состоящей из 9 юношей и 8 девушек, выбрать двух юношей и двух девушек, равно
| 1. | 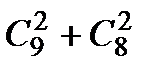
| 2. | 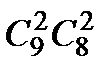
| 3. | 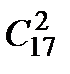
| 4. | 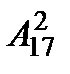
|
ВАРИАНТ 30
1. Как соотносятся мощности множеств N и А (N – множество натуральных чисел; A – отрезок действительной оси)?
| 1. | 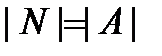
| 3. | 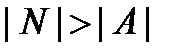
|
| 2. | 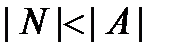
| 4. | 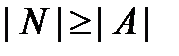
|
2. Построить выражение над множествами, которому соответствует заштрихованная область на приведенной диаграмме Эйлера–Венна.
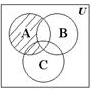
| 1. | 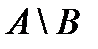
| 3. | 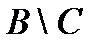
|
| 2. | 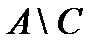
| 4. | 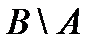
|
3. Отношение частичного порядка на множестве A, для которого любые два элемента из A сравнимы, называется отношением ____________ (ВПИШИТЕ НУЖНОЕ).
4. Даны пары <x, y>Îr, причем xÎ{0,...,8}, yÎ{0,...,9}
| x | 3 | 8 | 1 | 2 | 4 | 5 | 0 | 6 | 8 | 7 |
| y | 6 | 1 | 8 | 7 | 5 | 4 | 9 | 3 | 0 | 2 |
Приведенное отношение r
| 1. | не является функцией | 3. | только инъективная функция |
| 2. | только сюръективная функция | 4. | биективная функция |
5. Выявить свойства бинарного отношения быть богаче на множестве людей (не менее двух правильных ответов).
| 1. | рефлексивное | 4. | отношение эквивалентности |
| 2. | симметричное | 5. | отношение строгого частичного порядка |
| 3. | транзитивное | 6. | отношение линейного порядка |
6. Упростить выражение 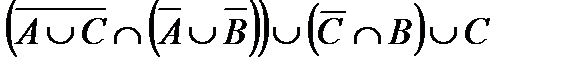
| 1. | 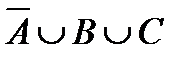
| 2. | 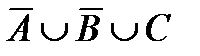
| 3. | 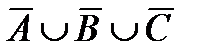
| 4. | 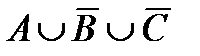
|
7. Мощность множества 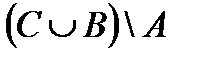 , если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
, если А = {x: xÎN и x < 8}, B = {x: xÎZ и (x + 1)2 < 32}
и С = {x: xÎZ и |x + 2| < 3}, равна
| 1. | 14 | 2. | 7 | 3. | 9 | 4. | 16 |
8. Найти биективное отображение 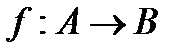 , если
, если 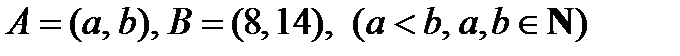 (
( 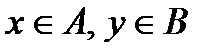 )
)
| 1. | y = (6x + 8b – 14a)/(b – a) | 3. | y = (x(b – a) – 8b + 14a)/6 |
| 2. | y = (x(b + a) – 8b + 14a)/6 | 4. | y = (x(b – 14) – 8b + 14a)/6 |
9. В кондитерской имеется 5 видов пирожных. Покупатель берет 3 пирожных. Сколькими способами он может это сделать? (Предполагается, что пирожных каждого вида ³ 3).
| 1. | 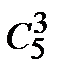
| 2. | 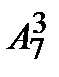
| 3. | 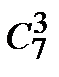
| 4. | 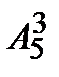
|
10. В лифт 10-этажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со 2-го) этаже. Сколькими способами два человека могут выйти на одном этаже, а третий – на другом:
| 1. | 108 | 2. | 120 | 3. | 216 | 4. | 240 |
Дата добавления: 2021-02-10; просмотров: 287; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
