Временная сложность вычислений (алгоритма)

Заключение

Общество 21 века – информационное, в нем все большее число задач решается методами дискретной математики. Сегодня дискретная математика стала теоретической основой решения задач с помощью вычислительной техники. Модели, методы дискретной математики являются хорошим средством для построения и анализа моделей в различных сферах человеческой деятельности, включая экономику, менеджмент и программирование. Язык дискретной математики настолько удобен, что фактически он стал метаязыком (языком описания) всей современной математики.

Теория множеств предоставляет удобные средства для описания многих математических идей. Теория графов находит применение, например, в геоинформационных системах. Существующие или вновь проектируемые дома, сооружения, рассматриваются как вершины, а соединяющие их дороги, инженерные сети, – ребра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или спланировать оптимальный маршрут. Булева алгебра позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.

Настоящее пособие знакомит с начальными сведениями данных разделов и призвано заинтересовать читателя в более глубоком их изучении.

СПИСОК ЛИТЕРАТУРЫ

1. Takes F.W., Kosters W.A. Determining the diameter of small world networks // Proceedings of the 20th ACM international conference on Information and knowledge management. New York: ACM, 2011. P. 1191–1196.

2. Ахметова Н.А., Гильмутдинова А.Я., Усманова З.М. Элементы дискретной математики. Функции алгебры логики. Теория графов. Элементы теории кодирования [Электронный ресурс]: учебное пособие. Уфа: УГАТУ, 2015.

3. Поречный С.С., Житникова Н.И., Федорова Г.И. Элементы теории множеств. Практикум по дисциплине «Дискретная математика». Уфа: УГАТУ. 2011. 45 с.

4. Поречный С.С., Житникова Н.И., Федорова Г.И. Теория графов. Практикум по дисциплине «Дискретная математика». Уфа: УГАТУ. 2011. 37 с.

5. Поречный С.С., Федорова Г.И., Михтанюк А.А. Алгебра логики. Практикум по дисциплине «Дискретная математика» Уфа: УГАТУ. 2011. 32 с.

6. Поречный С.С., Житникова Н.И., Михтанюк А.А. Дискретная математика. Комплект тестовых заданий: учебное электронное издание локального доступа. Уфа: УГАТУ, 2012. № гос. регистрации 0321201026.

7. Поречный С.С., Житникова Н.И., Михтанюк А.А. Элементы теории графов: учебное электронное издание локального доступа Уфа: УГАТУ, 2012. № гос. регистрации 0321201806.

8. Поречный С.С., Михтанюк А.А., Юсупова Л. Р. Элементы математической логики. Практикум: учебное электронное издание локального доступа. Уфа: УГАТУ, 2013. № гос. регистрации 0321302432.

9. Тимеряев Т.В., Ураков А.Р., Поречный С.С. Аппроксимация графов дорожных сетей Saarbrucken, Germany: LAP LAMBERT Academic Publishing OmniScriptum GmbH & Co. KG, 2015, 213 c.

10 Галиев Ш.И. Математическая логика и теория алгоритмов. – Казань: Издательство КГТУ им. А. Н. Туполева, 2002, 270 с.

Приложение

1. СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ С ПОМОЩЬЮ АЛГОРИТМОВ

Понятие о сложности

Существуют задачи, которые теоретически разрешимы, но при практической реализации требуют столь больших вычислений, что их решение практически неосуществимо. Следовательно, принципиальная алгоритмическая разрешимость еще не означает практическую реализуемость. Рассмотрим некоторые характеристики вычислений.

Считаем, что при вычислении используется алгоритм.

Различают сложность описания алгоритма и исходных данных, и сложность применения алгоритма к исходным данным.

Сложность описания алгоритма зависит от выбора того или иного способа задания алгоритма. Если такой способ выбран (машина Тьюринга, нормальный алгоритм или рекурсивное задание и т. д.), то под сложностью алгоритма может быть введена как длина записи алгоритма, так и длина встречающихся выражений и т. д. Например, для машины Тьюринга ее сложность может быть введена как число букв внешнего и внутреннего алфавитов.

& Определение. Неотрицательная функция g(n)есть O(f(n)) если существует такая постоянная c, что g(n) ≤ c·f(n) для всех, кроме конечного (возможно пустого) множества значений n, n 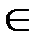{1, 2, 3,…}. В этом случае записываем: g(n) = О(f(n)).

Сложность исходных данных понимается как длина (размер) их записи. Размером входа, в общем случае, считают число символов, с помощью которых записан вход.

Пусть входом является целое число. Считаем, что число представлено в системе счисления с некоторым фиксированным основанием. В этих системах число символов, необходимых для представления целого числа n, равно ]log_A n[, где А ≥ 2– основание системы, а ]х[ обозначает наименьшее целое q, такое, что q ≥ x. Известно, что log_B n = (log₂n)/(log₂B), здесь log₂B является константой при фиксированном В. Таким образом, число символов, необходимых для представления целого числа n есть О(log₂n).

Пример

v Пусть требуется перемножить квадратные n × n матрицы А и В. Подходящей мерой сложности исходных данных будет число пропорциональное l = n², имея в виду, что для запоминания отдельного числа (элемента матрицы) выделен определенный объем памяти.

Во многих задачах входом является граф. Граф G = (V, X)
(|V| = n, |X| = m) можно, например, задать матрицей смежности А(G) = [a_ij] размера n × n. Ясно, что максимальное число возможных ребер в простом полном графе равно М = =O(n²).

Однако многие графы являются разреженными, т. е. число их ребер много меньше М. В этом случае можно задать граф перечислением его ребер, с помощью списков смежностей.

При задании списков смежностей для каждой вершины v 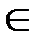V выписывается множество А(v) (А(v) V) вершин, смежных с v,
(рис. П1.1).

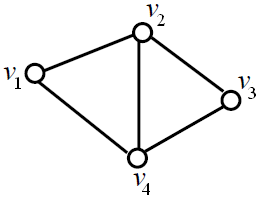
А(v₁) = {v₂, v₄};

А(v₂) = {v₁, v₃, v₄};

А(v₃) = {v₂, v₄};

А(v₄) = {v₁, v₂, v₃}.

Рис. П1.1. Пример графа и списков смежности

Размер этого представления зависит от суммы длин списков. Каждое ребро вносит вершину в два списка, поэтому сумма длин списков содержит 2m элементов. Но для различения вершин, как правило, вводятся числовые индексы. Так как имеется |V| вершин, то для индексов потребуется О(log₂n) двоичных или десятичных разрядов. Следовательно, при таком представлении графа G = (V, X) потребуется О(mlog₂n) символов.

Более экономной записью информации в ячейках памяти ЭВМ (выделенного для одного числа) можно добиться, что для задания графа G = (V, X) требуется O(m) ячеек памяти.

Сложность вычислений с помощью алгоритма понимается как функция от размера входа алгоритма. Для оценки сложности вычислений существует много критериев. Важными критериями являются: временная сложность, характеризующая время, затраченное на вычисление, и емкостная (ленточная) сложность, характеризующая необходимую для вычисления память, используемую для хранения промежуточных результатов.

Кроме того, сложность вычислений зависит от способа формулировки задачи.

Пример

v Требуется узнать, является ли натуральное число n простым или составным. Чтобы анализировать сложность задачи надо выяснить, как задано число n. Если n задано как произведение своих простых делителей: то задачи нет вообще; если n задано в унарной форме, т. е. n = 11…1, то сложность записи равна l = n (числу единиц), а сложность задачи, как можно показать, равна 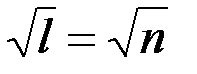(если использовать известный способ решения этой задачи – решето Эратосфена, состоящий в том, что число N последовательно делят на простые числа p₁, p₂,…, 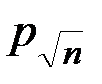. Если ни на одно из этих чисел N не делится, то оно простое, иначе составное). Если число n записано в десятичной форме, то сложность записи числа (длина записи) равна l = lgn, а сложность решения в этом случае равна 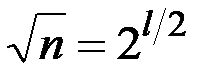, т. е. сложность решения представляет собой экспоненту от длины записи числа n.

Следует обратить внимание на то обстоятельство, что одной и той же задаче могут соответствовать разные языки, представляющие условия или входные данные задачи. Это связано со способами кодировки данных. Из всех языков представляющих исходную задачу, выбирается «разумный язык» или разумный способ кодировки ее условий.

Временная сложность вычислений (алгоритма)

Временная сложность вычислений (алгоритма) характеризует число операций для решения задачи заданного размера.

При решении однотипных задач с одинаковым размером входа может потребоваться различное число итераций для решения отдельных задач (этого типа), следовательно, и различное число операций.

& Определение. В ременная сложность алгоритма – число операций в худшем случае по всем входам размера (длины) n. Иначе говоря, это функция, которая каждому входу размера n ставит в соответствие максимальное (по всем индивидуальным задачам размера n) число операций, затрачиваемых алгоритмом на решение индивидуальной задачи этого размера.

Кроме меры сложности в наихудшем случае вводят временную сложность алгоритма Ав среднем на входе размера n:

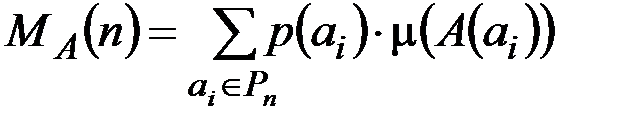здесь p(a _i) – вероятность появления задачи a _i; µ(A(a _i)) – число операций, затрачиваемых алгоритмом на решение индивидуальной задачи a _i; Р _n – множество рассматриваемых задач размера n, Р _n = {a _i}.

При изучении сложности алгоритма, в основном интересуются его поведением при применении его к очень большим входам. Различие между сложностями 10n³и 9n³считаются несущественными, более важен показатель степени, а не коэффициент. Как уже отмечено, сложность алгоритма оценивается асимптотической сложностью, т. е. порядком роста числа операций при неограниченном росте размера входа. Например, если вход размера n обрабатывается за время cn², где с – некоторая постоянная, то сложность этого алгоритма есть О(n²), т. е. постоянная с не содержится в оценке.

Для практических задач величина этого коэффициента может быть важна, если они различаются существенно. Если время работы алгоритмов А1и А2 пропорционально, например, 10¹⁰n²и 9n²соответственно, то практическое использование алгоритма А1проблематично.

Для решения выбранной задачи иногда можно использовать различные алгоритмы.

& Определение. Временная сложность задачи – временная сложность наилучшего алгоритма, известного для ее решения.

Выясним как изменяется эффективность различных алгоритмов с ростом быстродействия ЭВМ на которых реализуются эти алгоритмы.

Пусть имеем 5 алгоритмов различной сложности для решения одной и той же задачи. Положим, что каждое действие алгоритма осуществляется за 1 млс. Характеристики алгоритмов приведены в следующей таблице.

	Временная	Максимальный размер задачи,
Алгоритм	сложность	решаемой за указанное время
	алгоритма	1 с	1 мин	1 час
А1	N	1000	60 000	36 000 000
А2	N log₂N	140	4 893	2 000 000
А3	N²	31	244	1 897
А4	N³	10	39	153
А5	2^N	9	15	21

Из этой таблицы видно, что увеличение времени решения задачи, например с 1-й секунды до одного часа позволяет для алгоритма А1увеличить размер решаемой задачи в 3600 раз, а для алгоритма А5только в 2,33 раза.

Предположим, что быстродействие ЭВМ возросло в 10 раз. В нижеследующей таблице показано, как при этом возрастут размеры входов.

Алгоритм	Временная сложность алгоритма		Максимальный размер задачи
			до ускорения	после ускорения в 10 раз
А1		N	S1		10 S1
А2		N log₂N	S2		10 S2
А3		N²	S3		3,16 S3
А4		N³	S4		2,15 S4
А5		2^N	S5		S5 + 3,3

Из последней таблицы видно, что увеличение быстродействия в 10 раз дает возможность для алгоритма А1 увеличить размер входа в 10 раз, а для алгоритма А5 увеличение размера входа практически не произошло. Таким образом, чем большую временную сложность имеет алгоритм, тем меньшее улучшение дает увеличение быстродействия.

Дата добавления: 2021-02-10; просмотров: 64; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!