ЛЕКЦИЯ 7: «КОРРЕЛЯЦИОННЫЙ АНАЛИЗ. РЕГРЕССИОННЫЙ АНАЛИЗ»
Корреляционная зависимость.
Определение 1. Две случайные величины X и Y находятся в корреляционной зависимости, если каждому значению любой из этих величин соответствует определённое распределение вероятностей другой величины.
Определение 2. Условным математическим ожиданием дискретной случайной величины X при Y = y (y - определённое возможное значение Y) называют сумму произведений возможных значений величины X на их условные вероятности:
 ,
,
где 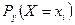 - условная вероятность равенства
- условная вероятность равенства  при условии, что Y = y.
при условии, что Y = y.
Для непрерывных величин
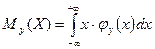 ,
,
где 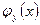 - плотность вероятности случайной непрерывной величины X при условии Y = y.
- плотность вероятности случайной непрерывной величины X при условии Y = y.
Условное математическое ожидание 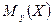 есть функция от y:
есть функция от y: 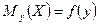 , которую называют функцией регрессии величины X на величину Y.
, которую называют функцией регрессии величины X на величину Y.
Аналогично определяется условное математическое ожидание случайной величины Y и функция регрессии Y на X:
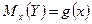 .
.
Уравнение 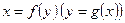 называют уравнением регрессии X на Y (Y на X), а линию на плоскости, соответствующую этому уравнению, называют линией регрессии.
называют уравнением регрессии X на Y (Y на X), а линию на плоскости, соответствующую этому уравнению, называют линией регрессии.
Линия регрессии Y на X (X на Y) показывает, как в среднем зависит Y от X (X от Y).
Коэффициент корреляции.
Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции.
Определение 1. Если X и Y – независимые случайные величины, то
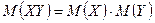 . (1)
. (1)
Если же X и Y не являются независимыми случайными величинами, то, вообще говоря,  .
.
|
|
|
Условились за меру связи (зависимости) двух случайных величин X и Y принять безразмерную величину r, определяемую соотношением
 (2)
(2)
или более кратко соотношением
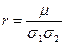 , (3)
, (3)
где
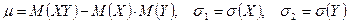 ,
,
и называемую коэффициентом корреляции.
Определение 2. Случайные величины X и Y называют некоррелированными, если r =0, и коррелированными, если 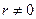 .
.
Свойства коэффициента корреляции.
1. Если X и Y независимые случайные величины, то коэффициент корреляции равен нулю.
2. 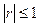 , при этом, если
, при этом, если 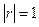 , то между случайными величинами X и Y имеет место функциональная, а именно, линейная зависимость.
, то между случайными величинами X и Y имеет место функциональная, а именно, линейная зависимость.
3. Как видно из формулы (2), коэффициент корреляции характеризует относительную величину отклонения математического ожидания произведения 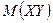 от произведения математических ожиданий
от произведения математических ожиданий 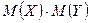 величин X и Y. Так как это отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между X и Y.
величин X и Y. Так как это отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между X и Y.
Линейная корреляция.
Определение. Корреляционная зависимость между случайными величинами X и Y называется линейной корреляцией, если обе функции регрессии f ( y ) и g ( x ) являются линейными. В этом случае обе линии регрессии являются прямыми; они называются прямыми регрессии.
|
|
|
Обозначим 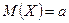 ,
, 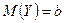 ,
,  ,
, 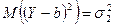 .
.
Уравнение прямой регрессии Y на X имеет вид
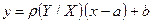 , (4)
, (4)
где коэффициент 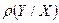 называется коэффициентом регрессии Y на X и вычисляется по формуле:
называется коэффициентом регрессии Y на X и вычисляется по формуле:
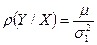 . (5)
. (5)
Аналогично уравнение прямой регрессии X на Y имеет вид
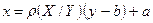 , (6)
, (6)
где коэффициент регрессии X на Y равен
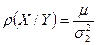 . (7)
. (7)
Уравнения прямых регрессий можно записать в более симметричном виде, если воспользоваться коэффициентом корреляции. С учётом этого коэффициента
 ,
, 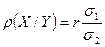 , (8)
, (8)
и поэтому уравнения прямых регрессий принимают вид
 ,
, 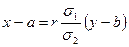 .
.
Из формулы (8) видно, что коэффициенты регрессии имеют тот же знак, что и коэффициент корреляции r, и связаны соотношением
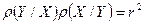 .
.
Расчёт прямых регрессий.
Пусть проведено n опытов, в результате которых получены следующие значения системы величин  :
: 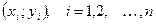 . За приближённые значения
. За приближённые значения  ,
,  ,
, 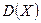 и
и  принимают их выборочные значения
принимают их выборочные значения
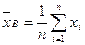 ,
,  ,
,  ,
, 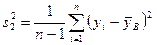 .
.
|
|
|
Оценкой для 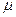 служит величина
служит величина
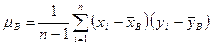 .
.
Заменяя в соотношениях (3), (4), (7) величины 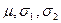 их выборочными значениями
их выборочными значениями 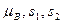 , получаем приближённые значения коэффициента корреляции и коэффициентов регрессий
, получаем приближённые значения коэффициента корреляции и коэффициентов регрессий
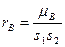 ,
, 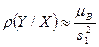 ,
, 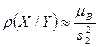
( 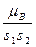 ,
, 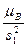 ,
,  - выборочные коэффициенты соответственно корреляции и регрессий).
- выборочные коэффициенты соответственно корреляции и регрессий).
Подставив в уравнения (5) и (6) вместо a, b, 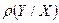 и
и 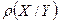 их приближённые значения, получим выборочные уравнения прямых регрессий:
их приближённые значения, получим выборочные уравнения прямых регрессий:
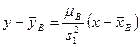 ,
,  .
.
Дата добавления: 2021-02-10; просмотров: 78; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
