Интегрирование методом замены переменной

Неопределенный интеграл

Первообразная и неопределенный интеграл

В данном разделе мы будем рассматривать следующую задачу: дана функция 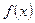, требуется найти такую функцию 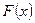, производная которой равна 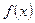, т.е. 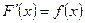. С точки зрения механики это означает, что по известной скорости движения материальной точки, необходимо восстановить закон ее движения.

Определение. Функция 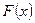называется первообразной функции 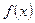на интервале 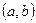, если 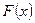дифференцируема на 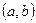и .

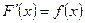Подобным образом можно определить понятие первообразной и на отрезке 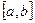, но в точках a и b необходимо рассматривать односторонние производные.

Пример 1. 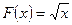- есть первообразная для функции 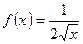на 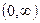, так как .

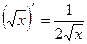Пример 2. 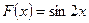- есть первообразная для функции 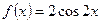на 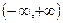, так как .

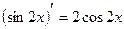Отметим, что если функция 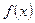имеет первообразную 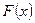, то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 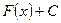, где С – некоторая постоянная.

Определение. Неопределенным интегралом от функции 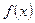(или от выражения 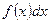) называется совокупность всех ее первообразных. Он обозначается следующим образом:

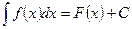Здесь 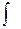называется интегралом; 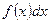- подынтегральным выражением; 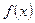- подынтегральной функцией, а х – переменной интегрирования.

Таким образом, неопределенный интеграл представляет собой семейство функций .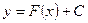

С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т.е. вдоль оси Y.

Отметим далее, что если функция 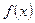непрерывна на отрезке 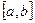, то для этой функции существует первообразная (а следовательно, и неопределенный интеграл).

Нахождение первообразной для данной функции 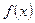называется интегрированием функции .

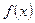Приведем ряд свойств неопределенного интеграла, вытекающих из его определения:

1. ;

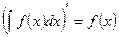2. ;

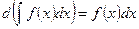3. 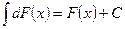, где С – постоянная величина;

4. 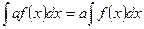, где а – постоянная;

5. ;

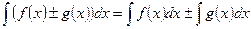6. Если - есть первообразная для , то

;

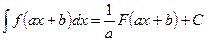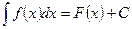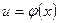7. Если и , то .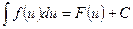

Прежде чем приступать к изучению методов интегрирования, приведем таблицу интегралов от простейших функций.

Таблица основных интегралов

I. ,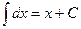

II. 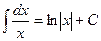, x>0,

III. 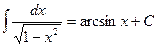, |x|<1,

IV. 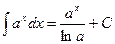, a>0, a¹1,

V. ,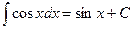

VI. ,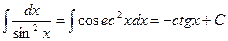

VII. ,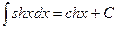

VIII. ,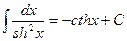

IX. ,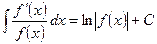

X. ,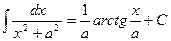

XI. ,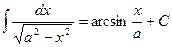

XII. ,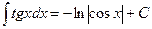

XIII. 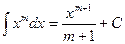, при ,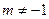

XIV. ,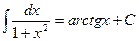

XV. ,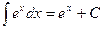

XVI. ,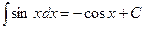

XVII. ,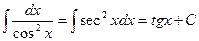

XVIII. ,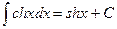

XIX. ,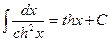

XX. ,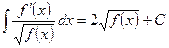

XXI. ,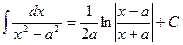

XXII. ,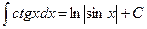

XXIII. ,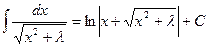

XXIV. ,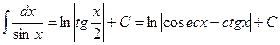

XXV. .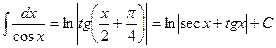

Приведем несколько примеров нахождения неопределенных интегралов, опираясь на их свойства и таблицу.

Пример 3. Найти интеграл .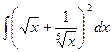

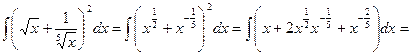
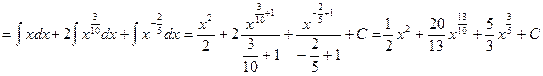Пример 4. Найти интеграл .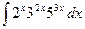

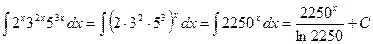Заметим, что свойство 7 позволяет значительно расширить таблицу основных интегралов с помощью приема подведения функции под знак дифференциала (это, вообще говоря, замена переменной).

Пример 5. Найти интеграл .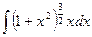

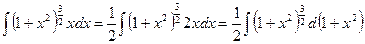Теперь переменной интегрирования служит выражение 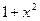и относительно этой переменной получается интеграл от степенной функции. Следовательно,

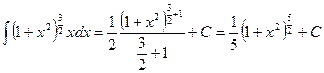Пример 6. Найти интеграл .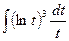

Выражение 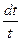можно записать как 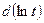, поэтому

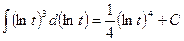Пример 7. Найти интеграл .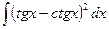

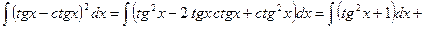
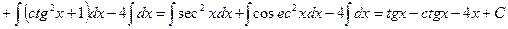Интегрирование методом замены переменной

Или способом подстановки

Пусть требуется найти интеграл 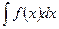, причем непосредственно подобрать первообразную для 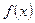невозможно, но нам известно, что она существует. В данном случае можно осуществить замену переменной в неопределенном интеграле с помощью подстановок двух видов:

1) положим в подынтегральном выражении 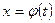, где 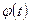- монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид

;

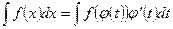2) если использовать подстановку вида 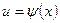, где и – новая переменная, то формула замены переменной при ней будет

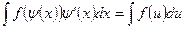Пример 8. Найдем интеграл .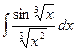

Произведем подстановку 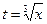, т.е. 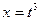. Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал: 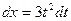. Следовательно,

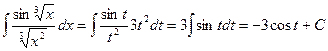Ответ должен быть выражен через старую переменную х. Подставляя в результат интегрирования 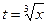, получим

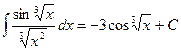Пример 9. Найти интеграл .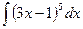

Полагая 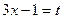, имеем 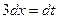, т.е. 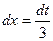. Отсюда получим

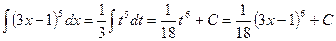Пример 10. Найти интеграл .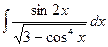

Произведем подстановку 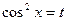, тогда 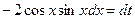, т.е. 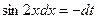. Следовательно,

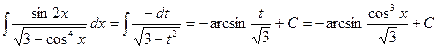Пример 11. Найти интеграл .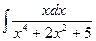

Преобразуем знаменатель дроби: 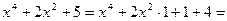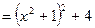. Произведем подстановку 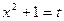, тогда 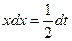. Отсюда

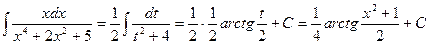Пример 12. Найти интеграл .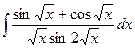

Полагая 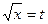, , 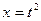, 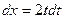получим

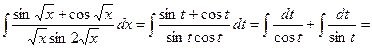
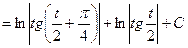Возвращаясь к старой переменной, получим

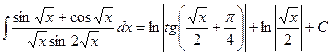Интегрирование по частям

Как следует из теоремы о дифференцировании произведения, интегрированием по частям называется нахождение интеграла по следующей формуле:

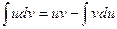Здесь 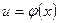, 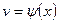- непрерывно дифференцируемые функции х. С помощью этой формулы нахождение интеграла 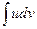сводится к отысканию другого интеграла 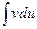. Ее применение целесообразно в том случае, когда последний интеграл либо проще исходного, либо подобен ему. При этом за и берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Отметим при этом, что для интегралов вида

, , ,

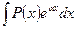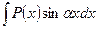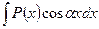где 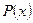- многочлен,

за и следует принять ,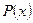

а за dv – соответственно выражения , , ;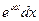

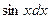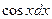для интегралов вида , , ,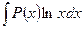

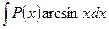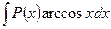за и принимают соответственно функции , , ,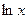

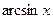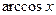а за dv – выражение .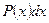

Пример 13. Найти интеграл .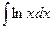

Положим 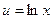, , 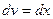тогда 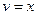, 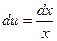. Используя формулу интегрирования по частям, получим

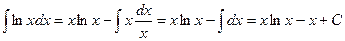Пример 14. Найти интеграл .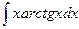

Пусть 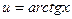, 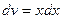; тогда 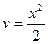, 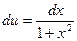. По формуле интегрирования по частям имеем

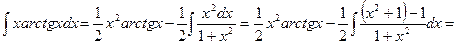
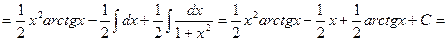
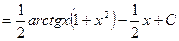Пример 15. Найти интеграл .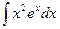

Положим 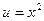, 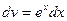; тогда 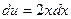, 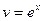.Применяем формулу интегрирования по частям:

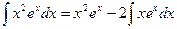Мы добились понижения степени х на единицу. Чтобы найти интеграл 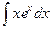, применим еще раз интегрирование по частям. Полагаем 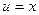, 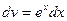; тогда 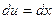, 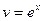. Окончательно получим

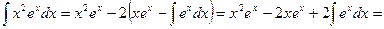
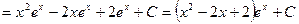Пример 16. Найти интеграл .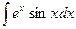

Пусть 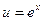, 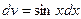; тогда 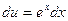, 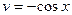. Следовательно,

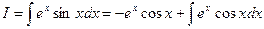Создается впечатление, что интегрирование по частям не привело к цели, поскольку интеграл не упростился. Попробуем, однако, еще раз проинтегрировать по частям. Приняв 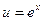, , 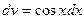откуда 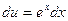, , 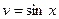получим

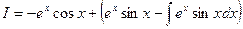
или

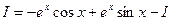Применив дважды операцию интегрирования по частям, мы в правой части получили исходный интеграл. Следовательно, приходим к уравнению с неизвестным интегралом I. Из этого уравнения находим

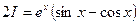, т.е. .

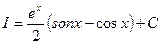В окончательном результате мы прибавили к найденной первообразной функции произвольную постоянную.

Дата добавления: 2021-02-10; просмотров: 35; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!