Нахождение интервалов выпуклости функции.
Достаточные признаки монотонности функции.
Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Точки локального экстремума.
. Число М называется локальным максимумом функции 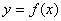 , если существует такая окрестность точки
, если существует такая окрестность точки 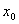 , что для всех
, что для всех 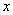 из нее выполняется неравенство
из нее выполняется неравенство 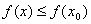 . При этом М=
. При этом М= 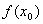 , а сама точка
, а сама точка 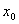 называется точкой локального максимума.
называется точкой локального максимума.
Определение 2. Число m называется локальным минимумом функции 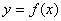 , если существует такая окрестность точки
, если существует такая окрестность точки 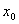 , что для всех
, что для всех 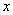 из нее выполняется неравенство
из нее выполняется неравенство 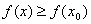 . При этом m=
. При этом m= 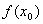 , а сама точка
, а сама точка 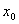 называется точкой локального минимума.
называется точкой локального минимума.
Определение 3. Локальный максимум и локальный минимум называются локальными экстремумами. Соответствующая точка 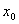 называется точкой локального экстремума.
называется точкой локального экстремума.
Необходимые и достаточные условия существования локального экстремума.
Пусть х0 – точка экстремума (максимума или минимума) функции у = f(x). Тогда в этой точке производная  равна нулю или не существует.
равна нулю или не существует.
Пусть  равны нулю (i = 1, 2, …, n), либо хотя бы одна из них не существует.
равны нулю (i = 1, 2, …, n), либо хотя бы одна из них не существует.
Пусть  -- критическая точка функции
-- критическая точка функции 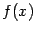 . Если функция
. Если функция 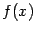 не убывает в некоторой левой окрестности
не убывает в некоторой левой окрестности 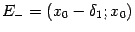 точки
точки  и не возрастает в некоторой её правой окрестности
и не возрастает в некоторой её правой окрестности 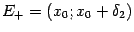 , то точка
, то точка  -- точка локального максимума.
-- точка локального максимума.
Достаточные условия.
|
|
|
Если же функция 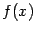 не возрастает в некоторой левой окрестности
не возрастает в некоторой левой окрестности 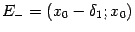 и не убывает в некоторой правой окрестности
и не убывает в некоторой правой окрестности 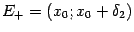 , то точка
, то точка  -- точка локального минимума.
-- точка локального минимума.
Доказательство. Если 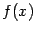 не убывает в
не убывает в  , то
, то 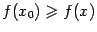 при всех
при всех 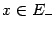 , поскольку из непрерывности
, поскольку из непрерывности 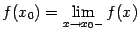 . Точно так же,
. Точно так же, 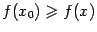 при всех
при всех  . Выберем из чисел
. Выберем из чисел  и
и 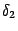 наименьшее:
наименьшее: 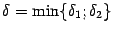 и рассмотрим симметричную окрестность
и рассмотрим симметричную окрестность 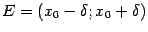 . При
. При  , очевидно,
, очевидно, 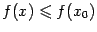 , то есть
, то есть  -- точка локального максимума.
-- точка локального максимума.
Вторая половина утверждения теоремы сводится к первой, если положить 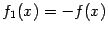 и заметить, что функция
и заметить, что функция 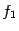 не убывает в
не убывает в  и не возрастает в
и не возрастает в 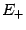 ; локальный максимум функции
; локальный максимум функции 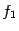 соответствует локальному минимуму функции
соответствует локальному минимуму функции 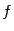 .
.
Нахождение интервалов монотонности. Найти интервалы монотонности функции f(x) (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f  (x). Для этого находят производную f
(x). Для этого находят производную f  (x) и решают неравенствоf
(x) и решают неравенствоf  (x)
(x)  0. На промежутках, где это неравенство выполнено, функция f(x) возрастает. Там, где выполнено обратное неравенство f
0. На промежутках, где это неравенство выполнено, функция f(x) возрастает. Там, где выполнено обратное неравенство f  (x)
(x)  0, функция f(x) убывает.
0, функция f(x) убывает.
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическимиточками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметьэкстремум.
|
|
|
Точки, в которых производная функции равна нулю, называются стационарными точками.
Наибольшее (наименьшее) значение функции на промежутке называется глобальным
экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Достаточный признак выпуклости функции на интервале.
Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Нахождение интервалов выпуклости функции.
Точка 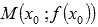 называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
|
|
|
Если функция y = f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство  (
( 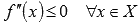 ), то график функции имеет выпуклость направленную вниз (вверх) на Х.
), то график функции имеет выпуклость направленную вниз (вверх) на Х.
Необходимое и достаточные условия перегиба.
Пусть график функции y = f(x) имеет перегиб в точке 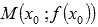 и имеет при
и имеет при 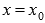 непрерывную вторую производную, тогда выполняется равенство
непрерывную вторую производную, тогда выполняется равенство  .
.
Пусть функция y = f(x) непрерывна в точке 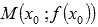 , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки
, имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от
. Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то
, вторая производная имеет разные знаки, то 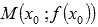 является точкой перегиба графика функции.
является точкой перегиба графика функции.
Если  , а
, а  , тогда
, тогда  является абсциссой точки перегиба графика функции y = f(x).
является абсциссой точки перегиба графика функции y = f(x).
Пусть 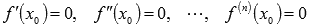 , а
, а 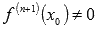 , тогда если n – четное число, то
, тогда если n – четное число, то  является абсциссой точки перегиба графика функции y = f(x).
является абсциссой точки перегиба графика функции y = f(x).
Асимптоты графика функции.
Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).
Асимптоты могут быть вертикальными, наклонными .
Если 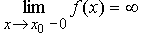 и (или)
и (или) 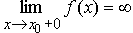 , то прямая y = x0 является вертикальной асимптотой
, то прямая y = x0 является вертикальной асимптотой
|
|
|
Полное исследование функции:
1. Область определения
2. Точки разрыва и вертикальные асимптоты.
3. Чётность, нечётность, периодичность.
4. Т. Пересечения с осями координат.
5. Исследование по первой производной.интервалы убывания или возрастания,т. Экстремума.
6. Исследование по второй производной, выпуклости вогнутости,точки перегиба.
7. Наклонные и горизонтальные асимптоты.
Дата добавления: 2020-12-12; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
