Примеры и разбор решения заданий тренировочного модуля
Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства 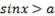 .
.
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
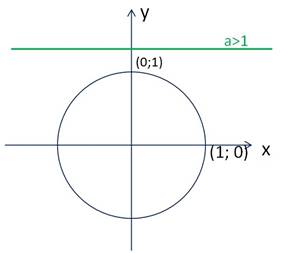
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на  (получим неравенство
(получим неравенство 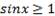 , то решением его будет множество точек, в которых
, то решением его будет множество точек, в которых 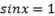 . Это числа
. Это числа 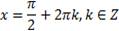 .
.
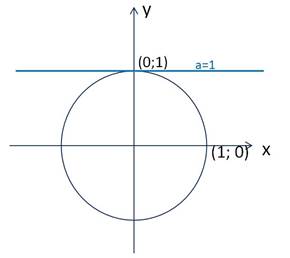
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
Рассмотрим теперь значение 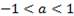 (рис.3).
(рис.3).
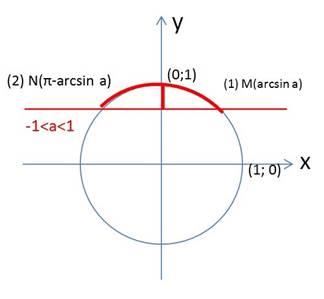
Рисунок 3 – Решение неравенства 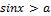
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1)  , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением
, конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением 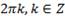 :
:
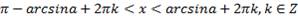
(для строгого неравенства) – множество интервалов;
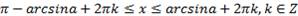
(для нестрогого неравенства) – множество отрезков.
Если значение a= – 1,то получим следующую картинку (рис. 4):
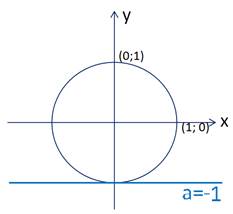
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства 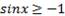 является любое действительное число. Если неравенство строгое, то решением неравенства
является любое действительное число. Если неравенство строгое, то решением неравенства 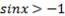 является любое действительное число, кроме чисел вида
является любое действительное число, кроме чисел вида 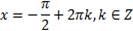 .
.
Наконец, если 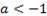 , то решением неравенства
, то решением неравенства 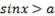 является любое действительное число.
является любое действительное число.
|
|
|
Решение неравенства 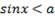 рассмотрим более коротко.
рассмотрим более коротко.
Очевидно, что если 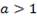 , то решением неравенства
, то решением неравенства 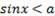 является любое действительное число.
является любое действительное число.
Если  , то решением неравенства
, то решением неравенства 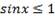 является любое действительное число, а решением неравенства
является любое действительное число, а решением неравенства 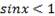 является любое действительное число, за исключением чисел вида
является любое действительное число, за исключением чисел вида 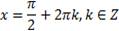 .
.
Если 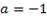 , то решением неравенства
, то решением неравенства 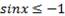 являются числа вида
являются числа вида 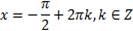 , а неравенство
, а неравенство 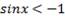 решений не имеет. То же самое можно сказать о решении неравенств
решений не имеет. То же самое можно сказать о решении неравенств 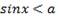 и
и 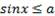 в случае
в случае 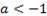 .
.
Случай 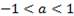 рассмотрим более подробно (рис. 5).
рассмотрим более подробно (рис. 5).
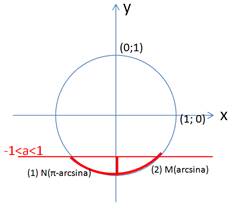
Рисунок 5 – Решение неравенства 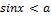
Решение неравенства 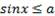 для
для 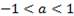 :
:
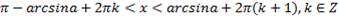 (для строгого неравенства) - множество интервалов;
(для строгого неравенства) - множество интервалов;
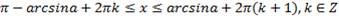 (для нестрогого неравенства) - множество отрезков.
(для нестрогого неравенства) - множество отрезков.
2. Теперь рассмотрим решение неравенств 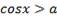 и
и 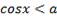 .
.
Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для 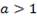 неравенство
неравенство 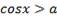 решений не имеет, а решением неравенства
решений не имеет, а решением неравенства 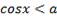 является любое действительное число.
является любое действительное число.
Для 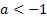 неравенство
неравенство  решений не имеет, а решением неравенства
решений не имеет, а решением неравенства 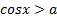 является любое действительное число.
является любое действительное число.
Рассмотрим случай 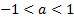 более подробно.
более подробно.
Рассмотрим решение неравенства 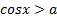 (рис. 6).
(рис. 6).
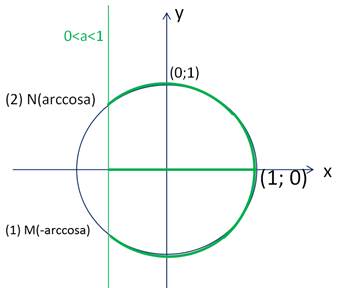
Рисунок 6 – Решение неравенства 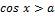
Множество решений этого неравенства:
|
|
|
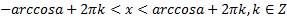 .
.
Теперь рассмотрим неравенство  (рис. 7).
(рис. 7).
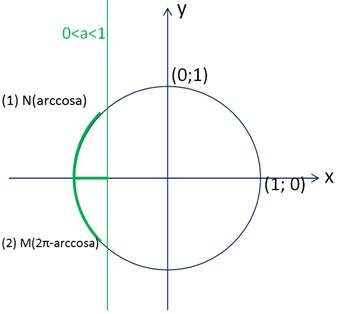
Рисунок 7 – Решение неравенства 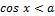
Множество решений этого неравенства:
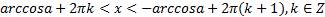 .
.
3. Теперь рассмотрим решение простейших неравенств 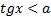 и
и 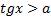 .
.
Сначала рассмотрим неравенство 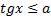 (рис. 8).
(рис. 8).
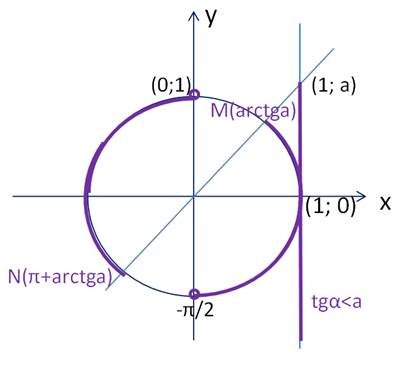
Рисунок 8 – Решение неравенства 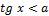
Множество решений этого неравенства:
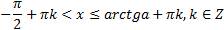 .
.
Соответственно, множество решений неравенства 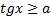 :
:
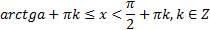 .
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Решите неравенство. Заполните пропуски
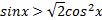
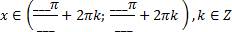
Решение:
Ведем новую переменную: 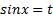 .
.
Вспомогательное неравенство имеет вид:
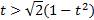
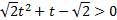
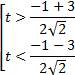 ,
, 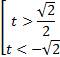 .
.
Вернемся к исходной переменной: 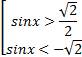 .
.
Второе неравенство решений не имеет. Решением первого неравенства является:
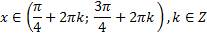 .
.
Ответ: 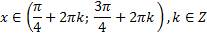 .
.
Пример 2.
Решите неравенство. Найдите коэффициенты
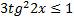
Решение:
Выразим 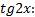
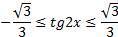
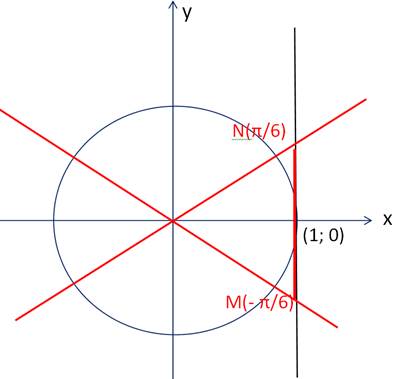
Рисунок 9 – решение неравенства 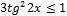
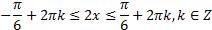
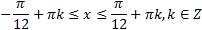
Ответ: 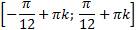
Дата добавления: 2021-02-10; просмотров: 58; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
