Решение задачи Коши для одномерного уравнения теплопроводности
Функция источника
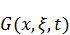 – температура, которая возникает в стержне, если в точке
– температура, которая возникает в стержне, если в точке 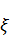 в начальный момент времени
в начальный момент времени 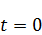 выделить какое-то количество тепла
выделить какое-то количество тепла 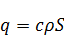 .
.
Принцип максимума и его следствия
Принцип максимума указывает, где могут располагаться в пределах ОДЗ максимальная и минимальная значения решения уравнения теплопроводности (однородного).
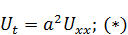
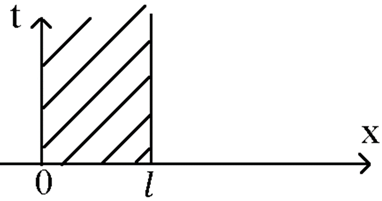
ОДЗ: 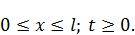
Принцип максимума. Формулировка: если функция 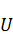 является решением уравнения теплопроводности, и в пределах ОДЗ она непрерывная, включая границы, то в этом случае ее максимальное значение может достигаться только на линиях
является решением уравнения теплопроводности, и в пределах ОДЗ она непрерывная, включая границы, то в этом случае ее максимальное значение может достигаться только на линиях 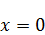 и
и 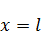 ,
, 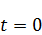 .
.
Нестрогое доказательство (от противного)
Предположим, что точка максимума лежит где-то внутри ОДЗ.
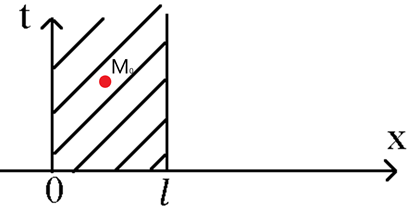
Замечание: если производная существует везде, значит функция гладкая.
В точке 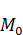 - справедливо условие максимума:
- справедливо условие максимума:
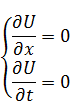
Условие максимальности: все вторые производные в точке 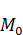 отрицательные.
отрицательные.
Из этого следует:
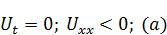
Предположив, что в точке 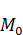 может быть максимум, возникает противоречие в уравнении
может быть максимум, возникает противоречие в уравнении 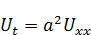 . Т. е. условия (а) несовместимы с уравнением.
. Т. е. условия (а) несовместимы с уравнением.
Доказательство нестрогое, потому что, вообще говоря, максимум может наблюдаться и в случае, если вторая производная была бы равна нулю.
Например, 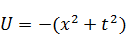 , ее вторая производная будет равна
, ее вторая производная будет равна 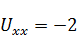 , максимум наблюдается в точке 0. Если посмотрим на функцию
, максимум наблюдается в точке 0. Если посмотрим на функцию 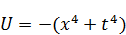 , ее максимум находится в точке 0, вторая производная этой функции
, ее максимум находится в точке 0, вторая производная этой функции
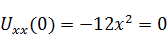 , равна нулю.
, равна нулю.
|
|
|
Строгое доказательство (от противного)
Для удобства введем некоторую верхнюю границу с уравнением 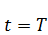 .
. 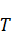 можно брать каким-угодно (линию можно поднимать сколь угодно высоко).
можно брать каким-угодно (линию можно поднимать сколь угодно высоко).
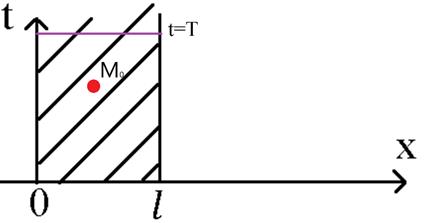
Будем предполагать, что максимальное значение будет находиться либо внутри ОДЗ, либо на линии 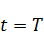 .
. 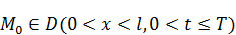 , T – любое число большее 0. Докажем, что это предположение является ложным. Надо показать, что найдутся точки внутри области определения (внутри ОДЗ) , которые не будут удовлетворять уравнению.
, T – любое число большее 0. Докажем, что это предположение является ложным. Надо показать, что найдутся точки внутри области определения (внутри ОДЗ) , которые не будут удовлетворять уравнению.
Замечание: непрерывная функция на ограниченном множестве всегда достигает своего максимального и минимального значения, которое является конечным.
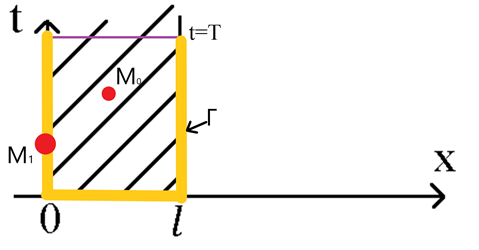
Точка 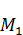 – точка максимального значения функции
– точка максимального значения функции 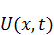 , когда
, когда 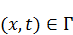 . Предположим
. Предположим 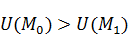 . Обозначим
. Обозначим 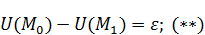 .
.
Введем новую функцию 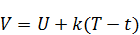 ,
, 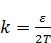 (поделили на 2 для надежности). Задача, узнать, где функция
(поделили на 2 для надежности). Задача, узнать, где функция 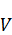 достигает своих максимальных значений.
достигает своих максимальных значений.
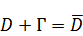 – замкнутая область, когда внутренняя часть и граница будут образовывать закрытое, замкнутое множество.
– замкнутая область, когда внутренняя часть и граница будут образовывать закрытое, замкнутое множество.
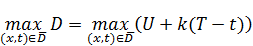
Замечание: максимум суммы всегда будет больше, чем разность максимумов.
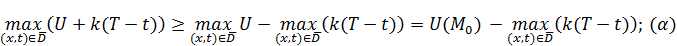
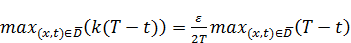 – максимальное значение скобки достигается при минимальном значении
– максимальное значение скобки достигается при минимальном значении 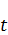 , это значение
, это значение 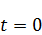 .
.
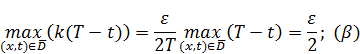
Учитывая 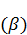 , выражение
, выражение 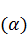 примет вид:
примет вид:
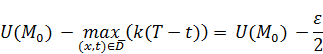
Это показывает, что максимальное значение на области 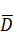 будет равняться
будет равняться 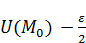 .
.
|
|
|
Теперь рассмотрим максимальное значение функции 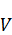 на границе Г:
на границе Г:
Замечание: максимальное значение от суммы будет меньше, либо равно сумме максимальных значений.
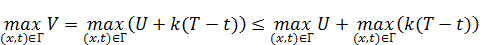
Максимальное значение на границе это 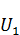 .
.
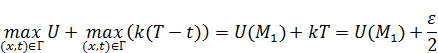
В итоге: 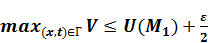 ;
; 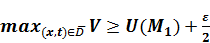 .
.
В ходе математических размышлений возникла нестыковка, требуется изменить условие (**). Изменим его на такое: 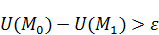 .
.
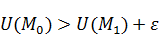
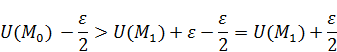
Символическая интерпретация:
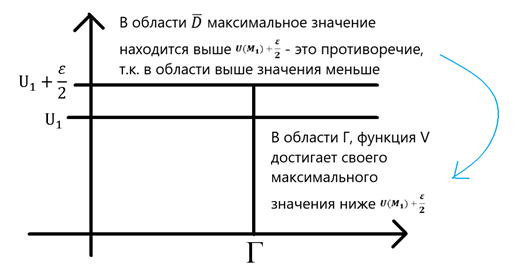
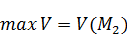
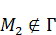
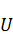 – непрерывная и дифференцируема,
– непрерывная и дифференцируема, 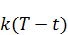 – также непрерывная и дифференцируемая, к тому же линейная, из этого следует, что функция
– также непрерывная и дифференцируемая, к тому же линейная, из этого следует, что функция 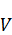 также будет являться непрерывной и дифференцируемой.
также будет являться непрерывной и дифференцируемой.
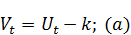
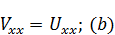
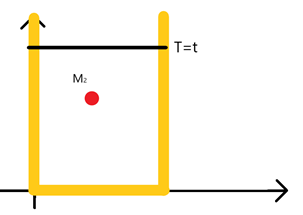
В точке экстремума 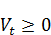 (критические точки могут находиться и на отрезке T=t).
(критические точки могут находиться и на отрезке T=t). 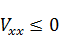 . Используя (a) и (b), получаем:
. Используя (a) и (b), получаем:
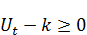
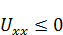
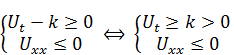
Вспоминая исходное уравнение 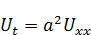 , видим, что наше предположение ложно – уравнение не выполняется.
, видим, что наше предположение ложно – уравнение не выполняется.
Следствия принципа максимума
1. Минимальное значение функции U также достигается на границе; если функция U подчиняется уравнению 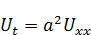 и для нее справедлив принцип максимума, то тогда функция
и для нее справедлив принцип максимума, то тогда функция 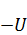 также является решением.
также является решением.
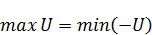
2. Если функция 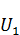 и
и 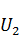 удовлетворяют теореме о максимуме (т. е. они подчиняются уравнению теплопроводности, непрерывности). И
удовлетворяют теореме о максимуме (т. е. они подчиняются уравнению теплопроводности, непрерывности). И 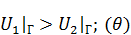 , то
, то 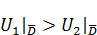 . Итак, если на границе одна функция всегда больше другой, то и внутри ОДЗ это условие будет выполнено. Если границе связь установили, то и внутри автоматически оно будет поддерживаться.
. Итак, если на границе одна функция всегда больше другой, то и внутри ОДЗ это условие будет выполнено. Если границе связь установили, то и внутри автоматически оно будет поддерживаться.
|
|
|
Доказательство
Рассмотрим функцию 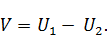 Очевидно, что функция
Очевидно, что функция 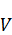 на границе:
на границе:
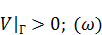 (в силу того, что условие (
(в силу того, что условие ( 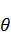 ) выполнено). Подставим функцию
) выполнено). Подставим функцию 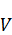 в уравнение:
в уравнение:
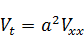
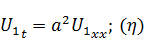
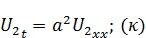
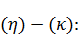
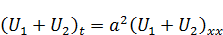 .
.
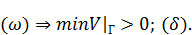
Одновременно с 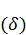 следует, что
следует, что 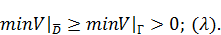
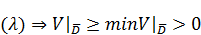
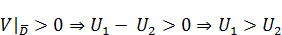
3. Если три функции 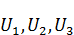 подчиняются условию теоремы о максимуме и на границе справедливо
подчиняются условию теоремы о максимуме и на границе справедливо 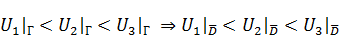 . Доказательство вытекает из свойства 2.
. Доказательство вытекает из свойства 2.
4. Если функция 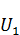 ,
, 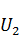 подчиняется условиям теоремы о максимуме и на границе справедливо условие
подчиняется условиям теоремы о максимуме и на границе справедливо условие 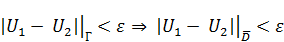 .
.
Доказательство
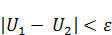
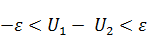
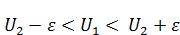
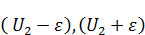 – удовлетворяют условиям теоремы о максимуме. Почему? А потому что уравнение
– удовлетворяют условиям теоремы о максимуме. Почему? А потому что уравнение 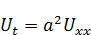 содержит в себе производные везде. И добавка и вычитание константы никак не сказывается, т. к. производные уничтожают эту добавку.
содержит в себе производные везде. И добавка и вычитание константы никак не сказывается, т. к. производные уничтожают эту добавку.
Особый смысл четвертого свойства: он называется – непрерывной зависимостью решения уравнения теплопроводности от граничных и начальных условий. Что под этим скрывается? Если немного изменить начальные условия, то и решение изменится немного. Небольшое изменение начальных и граничных условий приводит к такому же небольшому изменению решения. Это означает, что уравнение теплопроводности устойчиво.
|
|
|
Решение задачи Коши для одномерного уравнения теплопроводности
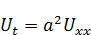
ОДЗ: 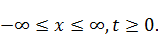
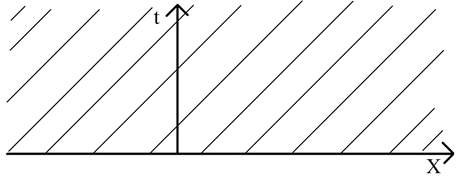
Похоже на задачу Коши волнового уравнения. Когда данная задача возникает на практике? Когда у нас длинный стержень и мы изучаем температуру где-то в средней его части. Концы находятся настолько далеко, что граничные условия, которые здесь закладываются или выполняются, абсолютно не влияют на решение в течении всего времени наблюдения. Да, возмущение некоторое может доходить, но на это понадобится настолько много времени, что к этому моменту эксперимент уже закончится.
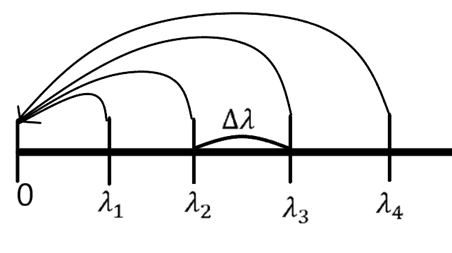
Проведем качественное рассуждение. Возьмем какой-то изначально ограниченный, небесконечный стержень в диапазоне от -L до L, а потом сделаем предельный переход:
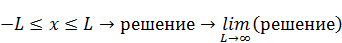
Т. е. мысленно будем отодвигать правую и левую концы на бесконечность и смотреть, что будет происходить с решением. Данный подход имеет ряд проблем. В зависимости от того, что ставить на границе, будем получать разные виды решения. И они не будут изначально так очевидно сходиться к одному результату. В связи с этим, эта привязка к граничным условиям немного подводит.
Пусть решается 1-я краевая задача.
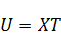
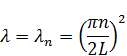
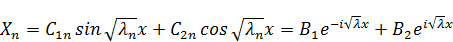
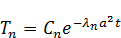
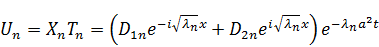
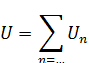
При увеличении 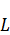 ,
, 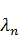 будут притягиваться к нулю. Это универсальное свойство задачи Штурма-Лиувилля:
будут притягиваться к нулю. Это универсальное свойство задачи Штурма-Лиувилля: 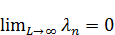 .
. 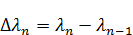 ,
, 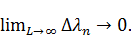
При 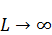 ,
, 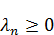 – любое число.
– любое число.
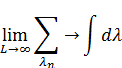
То тогда решение примет вид:
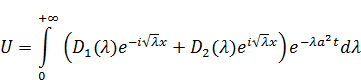
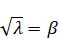
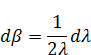
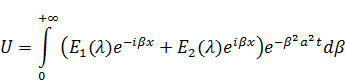
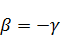
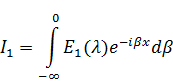
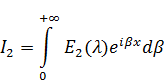
Решение будет иметь вид интеграла:
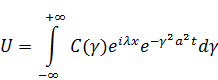
Дата добавления: 2021-02-10; просмотров: 80; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
