Решение однородных краевых для неоднородного волнового уравнения
Волновое уравнение
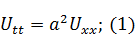
ОДЗ: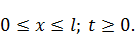 
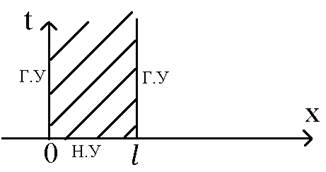
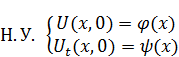
Первый тип краевой задачи:
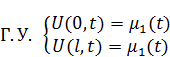
Возмущение указано снизу в начальных условиях, а также возмущение указано и слева и справа. Из этого вытекает, что волны, которые будут бежать по ОДЗ, будут бежать из начальных условий, потом они отразятся, повторно отразятся и так дальше.
Картина бегущих волн довольно сложная. Для решения этой задачи воспользуемся тем фактом, что уравнение однородное и линейное.
Так как уравнение относится к типу однородных и линейных, то это означает, что сумма двух или более решений снова является его решением.
Представим решение как сумму двух функций:
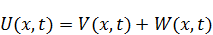
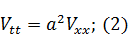
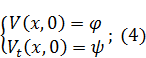
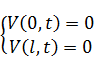Решение методом разделения переменных:
| 
|
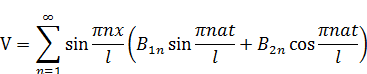
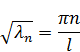
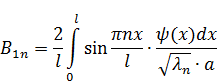
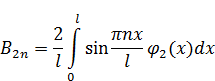
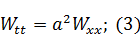
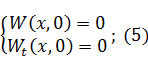
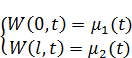
Замечание: по большому счету, мы возмущение, приводящее к колебанию, разделили на две части. Одно возмущение мы отнесли к одной задаче, другое возмущение к другой задаче.
Будет ли сумма этих двух условий порождать совпадение с исходной задачей? Проверим это:
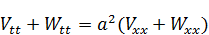
Производную за знак суммы можно выносить и тогда:
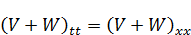
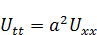
Для начальных условий:
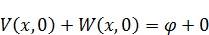
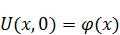
Задачу для функции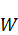 
нужно решать методом подбора. Для этого необходимо учесть следующее:
1. Граничные условия. Обязательно необходимо учесть это условие, иначе испортится задача для функции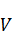 
;
2. Учет уравнения. Их учитываем по возможности;
3. Учет начальных условий. Их учесть практически невозможно.
|
|
|
Как проводится подбор?
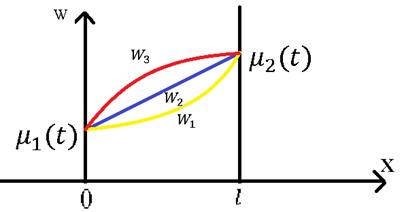
Мы видим поведение функции 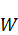в точке 0 и в точке 
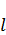. Сама функция 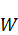это высота графика. Нужно придумать линию, которая могла бы соединить точк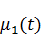и 
и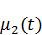 
. Какие линии могут соединять эти две точки? Через эти две точки могут проходить множество различных функций, но самая простая функций это линейная:
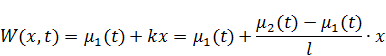
Функция найдена. Но эта функция не удовлетворяет 2-му условию – не выполняется уравнение:
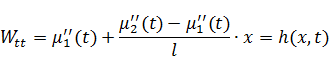
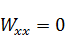
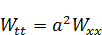
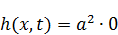
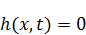
Но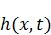 
не обязана, чтобы она равнялась 0 – в связи с этим, уравнение по большему счету не выполняется. Но, есл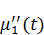и 
и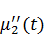 
будут равны нулю, например, если 
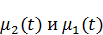константы (жесткое закрепление положений струн), то в таком случае удается выполнить уравнение.
Как можно попытаться уравнение учесть? Мы можем сказать, что функция 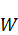зависит только от 
. 
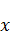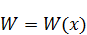, т. к. граничные условия не зависят от t:
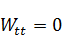
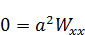
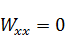
И, очевидно, из этого 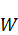будет линейной функцией:
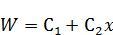
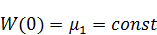
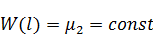
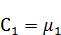
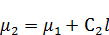
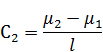
Если все-таки граничные условия зависят от времени, то упрощение становится для нас неподходящим и следует подойти к решению задачи по-другому. Тогда, допустим 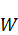зависит от x и t, таким образом:
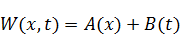
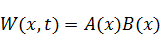
Однако, представление функции таким образом может нам не дать решения. В этом случае второе условия для метода подбора можно не выполнять.
|
|
|
Неучет уравнения и начальных условий требует корректировки решения и частных краевых задач. Что это означает? Прежде всего объявляем – попытка получить решение, удовлетворяющее уравнению 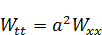, не дала результата. Для того, чтобы получить равенство, надо к уравнению (3) дописать добавку 
:
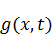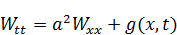
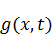– это результат того, что мы не смогли подобрать хорошую функцию. ( 
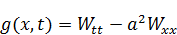, W – удовлетворяющая граничным условиям, но не удовлетворяющая уравнению и начальным условиям).
Также следует изменить начальные условия:
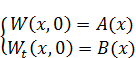
После подбора функции W она подставляется в свою краевую задачу на предмет корректности всех условий. После чего вычисляются компенсирующие слагаемые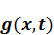 
, 
, 
.
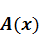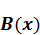Изменяя начальные условия для 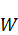, необходимо это учесть и для функции V. Начальные условия для функции V примут вид:
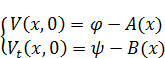
Если подбор привел к наличию слагаемого 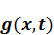, то для получения ответа исходной задачи требуется изменить вид решения, добавляя к нему третье слагаемое Z :
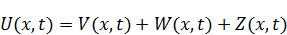
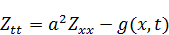
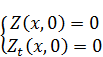
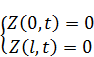
Задача с функцией Z является задачей с неоднородным волновым уравнением и однородными начальными и граничными условиями.
Решение однородных краевых для неоднородного волнового уравнения
|
|
|
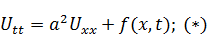
ОДЗ: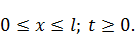
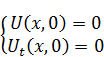
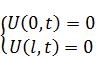
Замечание: если исходная краевая задача имеет неоднородное уравнение, начальные и граничные условия, то она, как и в предыдущем вопросе, будет решаться в виде суммирования двух функций.
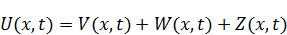
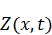– получит неоднородную добавку 
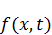и нулевые граничные и начальные условия;
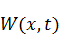– получит однородное уравнение и неоднородные граничные условия (решается подбором);
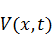– получит начальные неоднородные условия, а граничные условия и уравнение будут однородными.
Метод разложения по собственным функциям однородного уравнения (или однородной краевой задачи)
Решение представляется в виде:
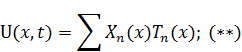
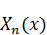– базисные, за ее нахождением необходимо обратиться к однородной краевой задаче.
Однородная краевая задача:
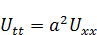
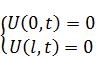
К ней, вообще говоря, также приписаны и начальные условия, но они сейчас не важны (Начальные условия нужны для нахождения T, а мы ищем X).
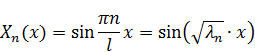
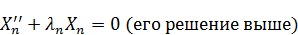
Замечание: базисные функции линейно независимы и ортогональны. Это означает, что коэффициенты разложения можно находить с помощью интеграла Фурье.
Подставим (**) в (*). Для внесения производной под знак бесконечной суммы требуется, чтобы ряд сходился равномерно и абсолютно.
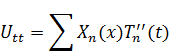
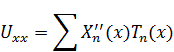
Вспоминаем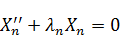 
: 
:
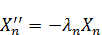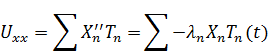
В итоге получаем:
|
|
|
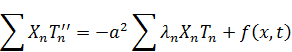
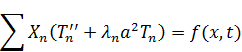
Обозначим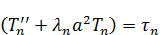 
.
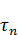- выступает в качестве коэффициента в разложении функции 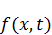по базису 
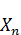. Из теории рядов Фурье, зная 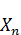и 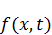, можно найти 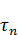. Формула для нахождения :
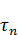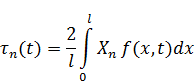
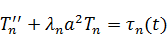– линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
Находим условия для T:
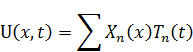
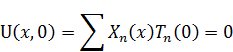
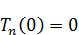
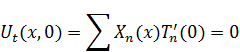
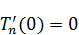
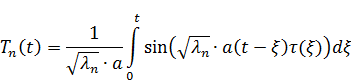
Дата добавления: 2021-02-10; просмотров: 240; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!