Элементы математической статистики
Теория вероятностей.
Согласно классическому определению вероятность события А равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т.е. 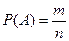 (1)
(1)
где P(A) – вероятность события;
m – число случаев, благоприятствующих событию А;
n – общее число случаев.
Пример 105. При бросании игральной кости возможны шесть исходов – выпадение 1,2,3,4,5,6, очков. Какова вероятность появления четного числа очков?
Решение. Все n = 6 исходов образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместимы. Событию А – «появление четного числа очков» благоприятствуют 3 исхода (случая) – 2,4 и 6 очков. По формуле (1) 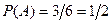 .
.
Основные свойства вероятности события:
· Вероятность любого события заключена между нулем и единицей, т.е.  1.
1.
· Вероятность достоверного события равна единице.
· Вероятность невозможного события равна нулю.
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего, в частности, методы решения комбинаторных задач – задач на подсчет числа различных комбинаций.
Пусть  – элементы конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.
– элементы конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.
|
|
|
Правило суммы. Если элемент Ai может быть выбран n1 способами, элемент A2 – другими n2 способами, A3 – отличными от первых двух n3 способами и т.д., Ak – nk способами, отличными от первых (k–1), то выбор одного из элементов A1 или A2,…, или Ak может быть осуществлен 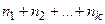 способами.
способами.
Пример . В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 2-го, а остальные – 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?
Решение. Деталь 1-го сорта n1 может быть извлечена 150 способами, 2-го сорта n2 - 120 способами. По правилу суммы существует 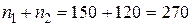 способов извлечения одной детали 1-го или 2-го сорта.
способов извлечения одной детали 1-го или 2-го сорта.
Правило произведения. Если элемент A1 может быть выбран n1 способами, после каждого такого выбора элемент A2 может быть выбран n2 способами и т.д., после каждого (k – 1) выбора элемент Ak может быть выбран nk способами, то выбор всех элементов A1, A2, …, Ak в указанном порядке может быть осуществлен n1 n2…nk способами.
Пример . В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?
Решение. Старостой может быть выбран любой из 30 учащихся, его заместителей – любой из оставшихся 29, а профоргом - любой из оставшихся 28 учащихся, т.е.  По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно
По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно 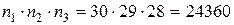 способов.
способов.
|
|
|
Если комбинации из n элементов по m отличаются либо составом элементов, либо порядком их расположения (либо и тем, и другим), то такие комбинации называют размещениями из n элементов по m. Число размещений из n элементов по m
 ,
, 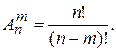
Если комбинации из n элементов по m отличаются только составом элементов, то их называют сочетаниями из n элементов по m. Число сочетаний из n элементов по m
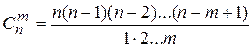 или
или 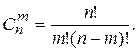
Так как 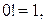 то
то 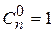 .
.
Если комбинации из n элементов отличаются только порядком расположения этих элементов, то их называют перестановками из n элементов. Число перестановок из n элементов
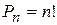
Пример . Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента – разрядники?
Решение. Пусть событие А – 3 выбранных наудачу студента – разрядники. Общее число случаев выбора 3 студентов из 30 равно 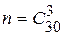 , так как комбинации из 30 студентов по 3 представляют собой сочетание, ибо отличаются только составом студентов. Точно так же число случаев, благоприятствующих событию А, рано
, так как комбинации из 30 студентов по 3 представляют собой сочетание, ибо отличаются только составом студентов. Точно так же число случаев, благоприятствующих событию А, рано 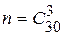 . Итак,
. Итак,
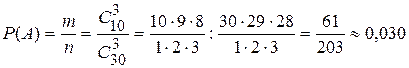
Пример . По условию лотереи «Спортлото 6 из 45» участник лотереи, угадавший 4,5,6 видов спорта из отобранных при случайном розыгрыше 6 видов спорта из 45, получает денежный приз. Найти вероятность того, что будут угаданы: а) все 6 цифр; б) 4 цифры.
|
|
|
Решение. 1. Пусть событие А – угадывание всех 6 видов спорта из 45. Общее число всех случаев, т.е. всех вариантов заполнения карточек спортлото, есть 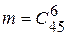 , так как каждый вариант заполнения отличается только составом видов спорта. Число случаев, благоприятствующих событию А, есть m = 1. Поэтому
, так как каждый вариант заполнения отличается только составом видов спорта. Число случаев, благоприятствующих событию А, есть m = 1. Поэтому
 .
.
2. Пусть событие В – угадывание 4 видов спорта из 6 выигравших из 45. Вначале найдем число способов какими можно выбрать 4 вида спорта из 6 выигравших, т.е. 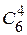 . Но это еще не все: к каждой комбинации 4 выигравших видов спорта из 6 следует присоединить комбинации 2 невыигравших видов из
. Но это еще не все: к каждой комбинации 4 выигравших видов спорта из 6 следует присоединить комбинации 2 невыигравших видов из 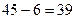 ; таких комбинаций
; таких комбинаций 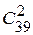 . По правилу произведения общее число случаев, благоприятствующих событию В,
. По правилу произведения общее число случаев, благоприятствующих событию В, 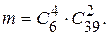 Итак,
Итак,
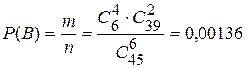 .
.
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.
Если А и В – совместные события, то их сумма А + В обозначает наступление события А или события В, или обоих событий вместе. Если А и В – несовместные события, то их сумма А + В означает наступление события А или события В.
|
|
|
Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.
Если А,В,С –совместные события, то их произведение АВС означает наступление события А, события В и события С.
Разностью А – В двух событий А и В называется событие, которое состоится, если событие А произойдет, а событие В не произойдет.
Теорема. Вероятность суммы несовместимых событий равна сумме вероятностей этих событий: P(A+B+…+K) = P(A) + P(B) +…+ P(K).
Следствие. Сумма вероятностей противоположных событий равна единице: 
Так, если к комплексу условий, при котором изучалась вероятность, добавить новое условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается 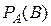 или
или 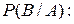
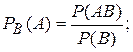
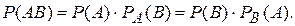
Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет, т.е.
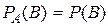 или
или 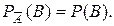
В противном случае, если  или
или  событие В называется зависимым от А.
событие В называется зависимым от А.
Пример Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только 2-й экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Решение. 1. Обозначим события: А i – студент сдаст i-й экзамен (i=1,2,3); В – студент сдаст только 2-й экзамен из трех. Очевидно, что 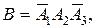 т.е. совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й. Учитывая, что события
т.е. совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й. Учитывая, что события 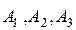 независимы, получим:
независимы, получим:
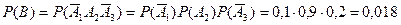 .
.
2. Пусть событие С – студент сдаст один экзамен их трех. Очевидно, событие С произойдет, если студент сдаст только 1-й экзамен их трех, или только 2-й, или только 3-й, т.е.
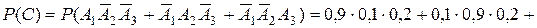
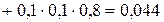 .
.
3. Пусть событие D – студент сдаст все три экзамена, т.е. D= А1А2А3. Тогда

4. Пусть событие Е – студент сдаст, по крайней мере, два экзамена. Очевидно, что событие Е означает сдачу любых двух экзаменов из трех или всех трех экзаменов, т.е. 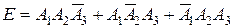 и
и
 .
.
5. Пусть событие F студент сдал хотя бы один экзамен. Очевидно, событие F представляет сумму событий С (включающих три варианта) и Е (четыре варианта), т.е.  (семь вариантов). Однако проще найти вероятность события F, если перейти к противоположному событию, включающему всего один вариант –
(семь вариантов). Однако проще найти вероятность события F, если перейти к противоположному событию, включающему всего один вариант – 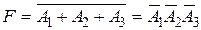 .
.
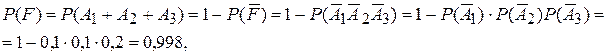 т.е. сдача хотя бы одного экзамена их трех является событием практически достоверным.
т.е. сдача хотя бы одного экзамена их трех является событием практически достоверным.
Пример 111. При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что:
а) двигатель начнет работать при третьем включении зажигания;
б) для запуска двигателя придется включать зажигание не более трех раз.
Решение
1. Обозначим события: А – двигатель начнет работать при каждом включении зажигания; В – тоже при третьем включении зажигания. Очевидно, что  и
и 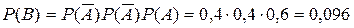 .
.
2. Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, при 2-м или при 3-м включении, т.е. 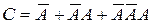 . Следовательно,
. Следовательно,
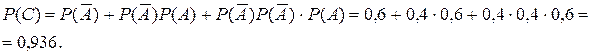
Теорема. Если событие F может произойти только при условии появления одного из событий (гипотез)  , образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события F:
, образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события F:
 . (51)
. (51)
Формулу (51) называют формулой полной вероятности.
Формула Байеса будет иметь вид
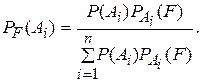 (52)
(52)
Пример . Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит: а) 1-му стрелку; б) 2-му стрелку?
Решение. Обозначим события:
 оба стрелка не попали в мишень;
оба стрелка не попали в мишень;
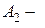 оба стрелка попали в мишень;
оба стрелка попали в мишень;
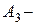 1-й стрелок попал в мишень, 2-й нет;
1-й стрелок попал в мишень, 2-й нет;
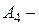 1-й стрелок не попал в мишень, 2-й попал;
1-й стрелок не попал в мишень, 2-й попал;
 в мишени одна пробоина (одно попадание).
в мишени одна пробоина (одно попадание).
Найдем вероятности гипотез и условные вероятности события F для этих гипотез:
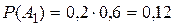 ,
, 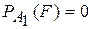
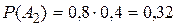 ,
, 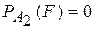
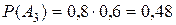 ,
, 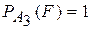
 ,
, 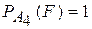 .
.
Теперь по формуле (52)
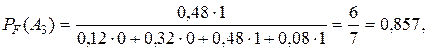
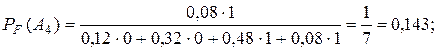
т.е. вероятность того, что попал в цель 1-й стрелок, при наличии одной пробоины, в 6 раз выше, чем для второго стрелка.
Формула Бернулли. Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Рm,n того, что событие А наступит m раз в n независимых испытаниях, составит
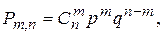 (53)
(53)
где р вероятность события А в одном испытании, q - противоположное испытание. Формулу (53) называют формулой Бернулли.
Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.
Решение. Вероятность изготовления бракованной детали 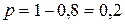 . Искомые вероятности находим по формуле (53):
. Искомые вероятности находим по формуле (53):
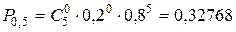 ;
; 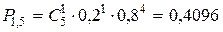 ;
;
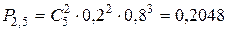 ;
; 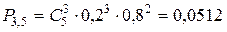 ;
;
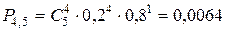 ;
; 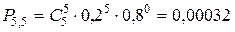 .
.
Математическим ожиданием или средним значением М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности:
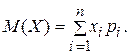 (54)
(54)
Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
 или D(x)=M(x2) - (M(x))2. (55)
или D(x)=M(x2) - (M(x))2. (55)
Средним квадратическим отклонением (стандартным отклонением или стандартом)  случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии:
случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии:
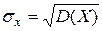 .
.
Пример . Вероятность совершить покупку равна 0,3 для первого покупателя, 0,5 – для второго, 0,6 – для третьего. Найти закон распределения случайной величины Х – числа покупателей, совершивших покупку. Найти числовые характеристики этой случайной величины.
Решение. Возможные значения случайной величины Х таковы:
X1 = 0, X2 = 1, X3 = 2, X4 = 3.
Обозначим события:
А1 – первый покупатель совершил покупку;
А2 – второй покупатель совершил покупку;
А3 – третий покупатель совершил покупку; события `А1,`А2,`А3 – им противоположные.
Находим вероятность pi = P(X = xi), i = 1,2,3,4, применяя теоремы сложения и умножения вероятностей, получаем:
P1 = P( x = 0) = P(`А1`А2`А3) = P(`А1) ×P(`А2) ×P(`А3) = 0,7 × 0,5 × 0,4 = 0,14;
P2 = P(x = 1) = P(А1`А2`А3, или `А1 А2`А3, или `А1`А2 А3) = P(А1`А2`А3) + +P(`А1 А2`А3) + P(`А1`А2 А3) = 0,3 × 0,5× 0,4 + 0,7× 0,5 ×0,4 + 0,7× 0,5× 0,6 = =0,41;
P3 = P(x = 2) = P(А1 А2`А3) + P( А1`А2 А3) + P(`А1 А2 А3) = 0,3 × 0,5×0,4 + +0,3×0,5×0,6 + 0,7 × 0,5 × 0,6 = 0,36;
P4 = P(x = 3) = P(А1 А2 А3) = 0,3 × 0,5 × 0,6 = 0,09.
Ряд распределения случайной величины Х имеет вид
| xi | 0 | 1 | 2 | 3 |
| Pi | 0,14 | 0,41 | 0,36 | 0,09 |
åPi = 0,14 +0,41 + 0,36 + 0,09 = 1.
Значит закон составлен, верно. Находим числовые характеристики случайной величины:
1. Математическое ожидание вычисляем по формуле (54):
М= М(х) = 0 × 0,14 + 1 × 0,41 + 2 × 0,36 + 3 × 0,09 = 1,4.
2. Дисперсию по формуле (55):
D(x) = (0 – 1,4)2 ×0,14 + (1 – 1,4)2 ×0,41 + (2 – 1,4)2 ×0,36 + (3 – 1,4)2 ×0,09 = =0,70.
3. Среднее квадратическое (стандартное) отклонение s(x) = 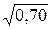 » 0,84.
» 0,84.
Пример . Закон распределения случайной величины Х дан ниже.
| Xi | -1 | 0 | 2 |
|
| Pi | 0,2 | 0,5 | 0,3 |
Найти функцию распределения этой случайной величины и построить ее график.
Решение. Известно, что функция распределения F(x) = P(X < x). Если x £ -1, то F(x)= 0, так как случайная величина не принимает ни одного значения меньшего –1. Если –1 < x £ 0, то в промежуток (- ¥; x) попадает 1 значение случайной величины x = -1 с вероятностью 0,2, следовательно, F(x) = P(x = -1) = 0,2. Если 0 < x £ 2, то в промежуток (- ¥; x) попадают 2 значения случайной величины, т.е. она может принять значения x = -1 или x = 0, следовательно, F(x) = P(x = -1) + P(x = 0) =
= 0,2+0,5= 0,7. Если 2< x < ¥, то в промежуток ( - ¥; x) попадают все значения случайной величины, поэтому F(x) = P(x = -1) + P(x = 0) + P(x = 2) = 1. Итак, получаем функцию распределения:
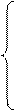 |
0, если x £ -1,
F(x) = 0,2, если –1 < x £ 0,
0,7, если 0 < x £ 2,
1, если x > 2.
Строим график этой функции.
 F(x)
F(x)






1


 0,7
0,7





 x
x
-1 0 1 2
Математическое ожидание непрерывной случайной величины вычисляется по формуле:
М (х)= 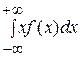 .
.
Дисперсия непрерывной случайной величины по формуле:
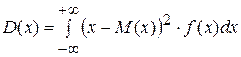
или
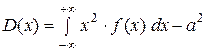 ,
,
где а = М(х).
Пример Задана функция распределения случайной величины Х
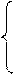 0, при х £ 0,
0, при х £ 0,
F(x) = х, при 0 < х £ 1, 
1, при х > 1.
Определить вероятность того, что в результате испытаний случайная величина примет значение большее 0,3, но меньшее 0,7. Найти плотность вероятности распределения случайной величины и дисперсию.
Решение. Вероятность того, что 0,3 < х < 0,7, найдем по формуле P(x1 < X < x2) = F(x2) – F(x1). Получаем P(0,3 < x < 0,7) = F(0,7) – F(0,3) =
 = 0,7 – 0,3 = 0,4. Плотность вероятности f(x) по определению есть F¢(x), т.е.
= 0,7 – 0,3 = 0,4. Плотность вероятности f(x) по определению есть F¢(x), т.е.
0, при х £ 0,
f(x) = 1, при 0 < х £ 1,
0, при х > 1.
Математическое ожидание определим по формуле :
M(x) = 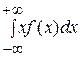 =
= 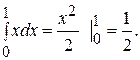
Дисперсию найдем по формуле (57):
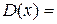
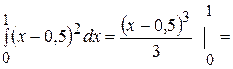 1/12.
1/12.
Элементы математической статистики





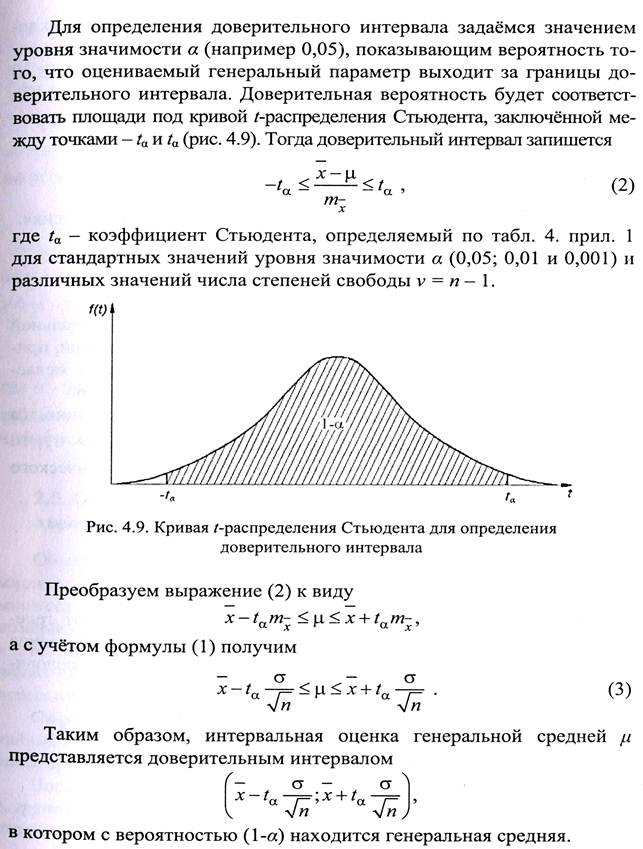
Перейдем теперь к интервальным оценкам.
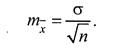
|

Принципиально важным вопросом является вопрос об объеме выборки.



Перейдем теперь к обработке результатов измерений по выборочным характеристикам.



Дата добавления: 2021-02-10; просмотров: 837; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
