Характеристики случайной величины
Закон распределения случайной величины
где x1, x2, …, xn - случайные величины, соответствующие полной группе событий, т. е. p1 + p2 + … + pn = 1.
При возрастании количества исходов полной группы событий закон распределения становится менее наглядным, и оценить наиболее вероятный исход становится достаточно трудно. Поэтому вводят характеристики случайных величин: математическое ожидание - ожидаемая величина в данном опыте, дисперсия - разброс значений.
Некоторые законы распределения
Биномиальное распределение
Пусть производится n испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события А в одном испытании равна р, то вероятность его ненаступления равна q = 1 - р.
Найдем вероятность того, что при n испытаниях событие А наступит m раз (m < n). Пусть событие А наступило в первых n испытаниях m раз и не наступило во всех последующих испытаниях. Это сложное событие можно написать в виде произведения:
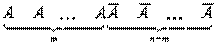
Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из n элементов по m элементов. Так как эти сложные события несовместимы, то вероятность их суммы равна сумме вероятностей. При этом вероятность каждого сложного события равна pm Ч qn-m. Вероятность появления события А m раз в n испытаниях равна:
|
|
|
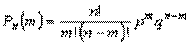(формула Бернулли).
Закон биномиального распределения
Нормальное распределение
Закон распределения вероятностей непрерывной случайной величины Х называется нормальным, если ее дифференциальная функция f (x) определяется формулой: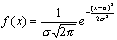 
где а совпадает с математическим ожиданием величины Х: а = М(Х), параметр a совпадает со средним квадратическим отклонением величины Х: σ = σ (Х).
График функции нормального распределения, как видно из рисунка, имеет вид куполообразной кривой, называемой Гауссовой, точка максимума имеет координаты (а; 
). Значит, эта ордината убывает с возрастанием значения s (кривая "сжимается" к оси Ох) и возрастает с убыванием значения s (кривая "растягивается" в положительном направлении оси Оу). Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным. Дифференциальная функция в случае такого распределения будет:
Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (a; b)
|
|
|
Пример 1.Бросаются две правильные однородные монеты. Сколько из них выпадает гербом кверху?
При подбрасывании двух монет пространство элементарных событий имеет вид:
U = {ЦЦ,ЦГ,ГЦ,ГГ}, где Ц- «цифра», Г- «герб».
Первый символ показывает, как выпала первая монета, а второй - вторая монета. Например, ЦГ означает, что первая монета выпала цифрой кверху, а вторая - гербом. Так как монеты правильные и однородные, то можно считать, что все элементарные события пространства U равновероятны, и тогда вероятность каждого из них равна %. Обозначим через X число монет, выпавших гербом кверху, составим таблицу:
| U | ЦЦ | ЦГ | ГЦ | ГГ |
| X | 0 | 1 | 1 | 2 |
| р |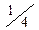 
| 
|
| 
|
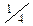
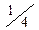
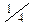
Так как элементарным событиям ЦГ и ГЦ соответствует одно и то же значение величины Х, равное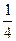 
, то можно полагать, что это значение величина X принимает с 4х вероятностью. Таким образом, значение величины X - число монет, выпавших гербом кверху и соответствующие им вероятности можно записать в виде таблицы.
| X | 0 | 1 | 2 |
| р |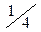 
| 
| 
|
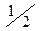
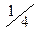
Итак, каждое значение величины X есть число, определяемое исходом опыта и зависящее от случая.
|
|
|
Определение 1.Случайной называется величина, которая в результате опыта принимает с определенной вероятностью, то или иное значение, зависящее от исхода опыта. Случайные величины обозначают прописными буквами латинского алфавита: X , Y , Z и т.д., а их значения - соответствующими буквами : х, у, z и т.д.,
Определение 2.Случайная величина называется дискретной, если множество её значений конечно или счётно, т.е. множество её значений представляет собой конечную последовательность х],х2,х3,...,хп. Вероятность того, что случайная величина X примет значение х, обозначают Р{х) = Р(Х = х)
Определение 3.Соответствие между возможными значениями xvx 2 ,..., xn случайной величины X и их вероятностями pvp 2 ,—, Pn называется законом распределения случайной величины X .
Закон распределения случайной величины может быть представлен в виде таблицы:
| X | х 
| х2 | ... | х
| ... | Х 
|
| р | Р1 | P 2 | ... | Pi | ... | Рп |
События X = xv X = х2,...,Х = хп образуют полную систему попарно несовместных событий, поэтому сумма их вероятностей равна единице р1 + р2 +... + рп = 1.
Пример 2.Закон распределения вероятностей случайной дискретной величины Х- числа очков, выпадающих при бросании правильной игральной кости, имеет вид, заданный таблицей:
|
|
|
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| р | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 |
2. Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) = С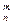 
*рт - qn m , m = 0,1,2,..., и. (1)
Определение. Закон распределения случайной величины X, имеющий вид:
| X | 0 | 1 | 2 | т | п | ||
| р | C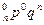 
| С 
| C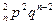 
| ... | С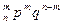 
| C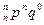 
|
называется биноминальным распределением.
Пример 3.Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P (Х = 0) = С4° • 0,9° • О,14 = 0,0001;
Р(Х = 1) = С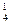 
•0,9 • 0,13 = 0,0036;
Р(Х = 2) = С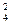 
•0,92 • О,12 = 0,0486;
Р(Х = 3) = С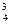 
•0,93 • О,1 = 0,2916;
P (Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
| X | 0 | 1 | 2 | 3 | 4 |
| р | 0,0001 | 0,0036 | 0,486 | 0,2916 | 0,6561 |
Пример 4. В ОТК измерялась длина в мм у 50 деталей, изготовленных на одном станке – автомате. В результате измерений получены следующие данные:
| 83 | 85 | 81 | 82 | 84 | 82 | 79 | 84 | 80 | 81 |
| 82 | 82 | 80 | 82 | 80 | 82 | 83 | 84 | 79 | 83 |
| 79 | 82 | 83 | 85 | 82 | 82 | 81 | 80 | 82 | 82 |
| 83 | 80 | 82 | 85 | 81 | 83 | 81 | 81 | 83 | 82 |
| 81 | 85 | 83 | 79 | 81 | 85 | 81 | 84 | 81 | 82 |
Требуется произвести первичную статистическую обработку данных:
1) Составить статистический ряд распределения частот и относительных частот длины деталей (случайная величина Х)
2) построить полигоны частот и относительных частот
3) найти эмпирическую функцию распределения и построить ее график
РЕШЕНИЕ:
1) Для составления статистических рядов исходные данные располагаются в порядке возрастания, затем подсчитываются частоты ni и относительные ni/n появление каждого из наблюдаемых значений (n=50).
| Наблюдаемые значения | 79 | 80 | 81 | 82 | 83 | 84 | 85 |
| Подсчет частоты | 4 | 5 | 10 | 14 | 8 | 4 | 5 |
| Относительные частоты | 0,08 | 0,1 | 0,2 | 0,28 | 0,16 | 0,08 | 0,1 |
2) Изобразим полигон частот и относительных частот
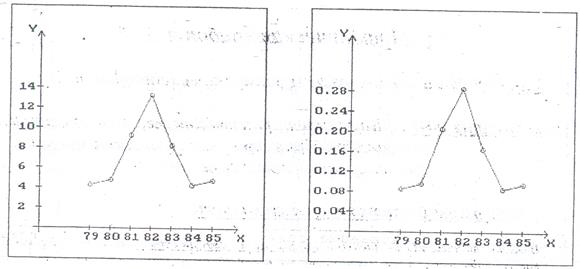
3) Эмпирическая функция распределения F*(x) определяется как отношение накопленных частот n*, т.е числа выборочных значений меньших х, объему выборки n.
| При х ≤ 79, | nx = 0, | F*(x) = 0/50 = 0 |
| При 79 < x ≤ 80, | nx = 4, | F*(x) = 4/50 = 0,08 |
| При 80 < x ≤ 81, | nx = 4+5=9, | F*(x) = 9/50 = 0,18 |
Аналогично вычисляются значения F*(x) на других интервалах.
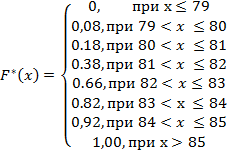
График функции F*(x):
Характеристики случайной величины
1. Математическое ожидание
Кроме закона распределения, который даёт полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. Среди числовых характеристик весьма важной является математическое ожидание,которое указывает, какое среднее значение случайной величины следует ожидать в результате испытаний или наблюдений.
Определение 1.Математическим ожиданием М(Х) дискретной случайной величины X называется сумма произведений всех её возможных значений х, на их вероятности pi :
М(Х) = ххрх +х2р2+... + х„р„ = 
Пример 1.Найти математическое ожидание М(Х) случайной величины X, зная закон её
распределения.
| X | -1 | 0 | 1 | 2 | 3 |
| р | 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение: по формуле (1) находим
М(Х) = -1*0,2 + 0*0.1 + 1*0,25 + 2*0,15 + 3*0,3 =1,25. Приведём без доказательства свойства математического ожидания:
1. Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CM(X)
2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий (теорема математических ожиданий):
М(Х + Y ) = М(Х) + M ( Y ).
3. Математическое ожидание постоянной величины С равно самой этой величине:
М(С)=С
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий (теорема умножения математических ожиданий):
m(xy)=m(x)-m(y).
Пример 2.Куплено 100 лотерейных билетов, причем на каждый из 10 билетов выпал выигрыш в 50 руб., 5 билетов -100 руб. 2 билета -300руб. Найти средний выигрыш, выпавший на один
билет.
Решение: введём случайную величину Х- размер выигрыша. Тогда эта случайная величина принимает следующие значения х, = 0, х2 = 50, х3 = 100, х4 = 300, а вероятность того,
что р(Х = 50) =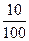 
= 0,1; р(Х = 100) = 
= 0,05; р(Х = 300) =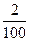 
= 0,02 и значит
р(Х = О) = 1 - 0,1 - 0,05 - 0,02 = 0,83. Значит случайная величина X имеет закон распределения:
| х | 0 | 50 | 100 | 300 |
| Pi | 0,83 | О,1 | 0,05 | 0,02 |
Тогда средний выигрыш выпавший на один билет есть М ( X ), поэтому
М(х) = 0 • 0,83 + 50 • 0,1 +100 • 0,05 + 300 • 0,02 = 16(руб).
2.Дисперсия случайной величины.
Рассмотрим следующий пример.
Пример 3. Найти математическое ожидание случайных величиной Y , зная законы их распределения.
| X | -8 | -4 | L -1 | 1 | 3 | 7 |
| р | 1/ 12 | 1 /6 | 1/4 | 1/ 6 | 1/12 | 1/ 4 |
|
| ||||||
| Y | -2 | -1 | 0 | 1 | 2 | 3 |
| Р | 1/ 6 | 1 /6 | 1/12 | 1/3 | 0 | 1/4 |
По формуле (1) имеем М(х) =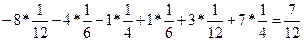 
M(y) =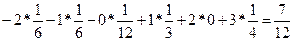 
Мы получили любопытный результат: законы распределения величиной Г разные, а их математические ожидания одинаковы.
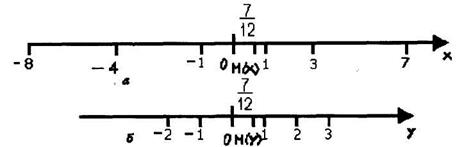
Из рисунка видно, что значения величины Y более сосредоточены около математического ожидания М(У), чем значения величины X , которые разбросаны относительно ее математического ожидания М(х).
Основной числовой характеристикой степени рассеяния значений случайной величины X относительно ее математического ожидания М(х) является дисперсия, которая обозначается через D ( X ).
Определение 2. Отклонением называется разность между случайной величиной X и ее математическим ожиданием Х-М(х).
Заметим, что отклонение X - М(х) и его квадрат ( X - M ( x ))2 также являются случайными величинами. Причем если X случайная величина распределена по закону,
| X | ||||
| р | Р\ | Pi | ... | Рп |
то квадрат её" отклонения имеет следующий закон распределения
| (x-M(x)f | (х,-м(х)У | (х2-м(х)У | (xn-M(X)f | |
| р | P 1 | Рг | Рп |
Введём теперь определение дисперсии случайной величины X .
Определение 3. Дисперсией случайной дискретной величины X называется математическое ожидание квадрата ее отклонения:
D ( X ) = M ( X - M ( x )2) (2)
Приведем без доказательства некоторые свойства дисперсии.
Дисперсия постоянной величины С равна нулю: D ( c ) = О
Если Х- случайная величина, С - постоянная, то D ( CX ) = C 2 D ( x ) и D { X + С) = D ( X )
Если X u Y - независимые случайные величины, то D ( X + Y ) = D ( x ) + D ( Y )
Для вычисления дисперсий более удобной является формула
D ( X )= M ( X 2 )- M ( X ) Y (3)
Пример 4. Случайная дискретная величина распределена по закону
| X | -1 | 0 | 1 | 2 |
| р | 0,2 | од | 0,3 | 0,4 |
Найти: D(X).
Сначала находим М(х) = -1 • 0,2 + 0 • 0,1 +1 • 0,3 + 2 • 0,4 = 0,9, а затем
М(Х2)= 1-0,2 + 0-0,1 + 1-0,3 + 4- 0,4 = 2,1.
По формуле (3) имеем D ( x ) = м(х2)- М2 ( X ) = 2,1 - 0,81 = 1,29.
Пример 5. Сравнить дисперсии случайных величин Х и Y , заданных законами распределения
| X | -1 | 1 | 2 | 3 |
| р | 0,48 | 0,01 | 0,09 | 0,42 |
| Y | -1 | 1 | 2 | 3 |
| Р | 0,19 | 0,51 | 0,25 | 0,05 |
Находим
М ( Х) = (-1) • 0,48 +1 • 0,01 + 2 • 0,09 + 3 • 0,42 = 0,97;
М(х2) = 1 * 0,48 +1 • 0,01 + 4 • 0,09 + 9 • 0,42 = 4,63;
D ( X ) = 4,63 -0,972 =3,69;
M(Y ) = (-1)*0,19 +1 • 0,51 + 2 • 0,25 + 3 • 0,05 = 0,97
M(Y2)=1*0,19 +1*0,51+ 4*0,25+ 9*0,05 = 2,15;
D ( Y ) = 2,15 -0,972 =1,21.
Полученные результаты показывают, что несмотря на то, что значения и математические ожидания случайных величиной У одинаковы, их дисперсии различны, причем D ( x )> D ( y ). Это означает, что случайная величина Y с большей вероятностью принимает значения, близкие к математическому ожиданию, чем случайная величина X .
Пример 6. Найти числовые характеристики (n = 50)
| Наблюдаемые значения | 79 | 80 | 81 | 82 | 83 | 84 | 85 |
| частоты | 4 | 5 | 10 | 14 | 8 | 4 | 5 |
1) Выборочное среднее
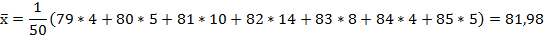
2) Выборочная дисперсия:
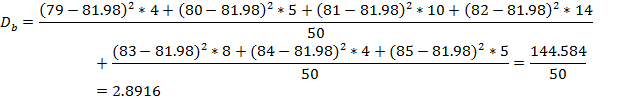
3) Выборочное среднее квадратическое отклонение:
Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) = С 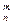*рт - qn m , m = 0,1,2,..., и. (1)
Определение. Закон распределения случайной величены X, имеющий вид:
| X | 0 | 1 | 2 | т | п | ||
| р | C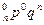
| С
| C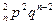
| ... | С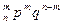
| C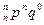
|
называется биноминальным распределением.
Пример 3.Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P (Х = 0) = С4° • 0,9° • 0,14 = 0,0001;
Р(Х = 1) = С 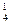* 0,9 • 0,13 = 0,0036;
Р(Х = 2) = С 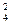* 0,92 • 0,12 = 0,0486;
Р(Х = 3) = С 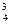* 0,93 • 0,1 = 0,2916;
P (Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
| X | 0 | 1 | 2 | 3 | 4 |
| р | 0,0001 | 0,0036 | 0,486 | 0,2916 | 0,6561 |
Дата добавления: 2021-02-10; просмотров: 52; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!