Построение эпюр внутренних усилий
СТЕРЖНЕВЫЕ СИСТЕМЫ
Расчёт статически неопределимых систем методом сил
Основная система и сущность метода
Статически неопределимыми называют системы, в которых невозможно определить все реакции в связях закрепления, а также внутренние усилия в элементах системы из уравнений статического равновесия. Но термин “лишние связи” является условным, поскольку при их отсутствии прочность и жёсткость системы значительно снижается. Этот термин означает, что связи лишние только в плане превышения их количества числа независимых уравнений равновесия.
Степень статической неопределимости можно определить как разность между числом искомых усилий и числом независимых уравнений равновесия, которые можно составить для рассматриваемой системы.
Для плоской системы положение жёсткого тела характеризуется тремя независимыми параметрами – двумя координатами и углом поворота, следовательно для равновесия на плоскости достаточно наложение трёх внешних связей, что соответствует и трём независимым уравнениям равновесия. Если плоская система состоит из Д жёстких тел (дисков), то количество параметров, определяющих положение этой системы будет равно ЗД. Если они соединены шарнирами, то каждый шарнир, соединяющий две части системы, разрешая взаимный поворот, устраняет возможность взаимного смещения, т.е. уменьшает количество возможных перемещений системы, накладывая две дополнительные связи. Каждый из опорных стержней устраняет возможность перемещения системы в соответствующем направлении. Тогда степень статической неопределимости, определяемую внешними связями можно подсчитать по формуле:
|
|
|
К=ЗД-2Ш-С,
где: Д- число частей системы, каждая из которых может рассматриваться как абсолютно жёсткое тело.
Ш- количество простых шарниров в системе, соединяющих два “диска”.
С- число опорных стержней.
Если К=0, то имеем статически определимую систему, если К<0 – статически неопределимую.
Для расчёта статически неопределимой системы дополнительно к уравнениям статики необходимо составить К уравнений совместности перемещения в точках системы.
Для заданной системы (рис. 12.1 а)
К=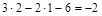 
Следовательно система дважды статически неопределима, имеются две лишних связи. Если у заданной системы отбросить две “лишних” связи то образуем основную систему. Основная система статически определима, но при её образовании необходимо обеспечить, что бы она не превратилась в механизм. Эта система может быть эквивалентна исходной, если к ней будут приложены в на-правлении отброшенных связей усилия Х1 и Х2 (рис. 12.1, б) значения которых следует определить из ограничений (совместности перемещений), которые накладывали отброшенные связи: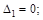 
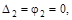т.е. перемещения в горизонтальном направлении правой опорной точки и угол поворота опорного сечения правой стойки равны нулю.
|
|
|
Эти усилия рассматриваются как основные и дают название метода расчёта - метод сил. Определив усилия в “лишних связях”, задача оказывается статически определимой. Для определения перемещений следует воспользоваться универсальным методом-методом Мора, получившего название по имени немецкого учёного, предложившего его.
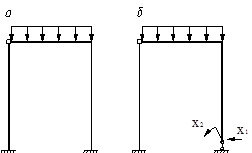
. Рис. 1
2.Определение перемещений методом Мора
При использовании этого метода (в литературе его называют: методом возможной работы; методом фиктивной нагрузки; методом единичной нагрузки) необходимо рассматривать две системы нагрузок, действующих на конструкцию. Первая система включает все реальные нагрузки, а вторая система включает только единичную нагрузку, которая действует на конструкцию. Еди-ничная нагрузка представляет собой фиктивную или искусственно введённую нагрузку, которая позволяет определить перемещение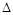 
конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении искомого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.
|
|
|
Действующая на конструкцию единичная нагрузка, которая представляет собой вторую систему нагрузок, вызывает возникновение реакций опор и внутренних усилий, которые обозначим через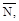 
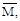
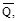
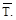Вместе с единичной нагрузкой и реакциями опор они образуют систему сил, которая находится в равновесии. Если конструкции предать малую возможную деформацию, в качестве которой возьмем действительные деформации конструкции, создаваемые первой системой нагрузок, то возможная работа внешних сил будет представлять
собой только работу, совершаемую самой единичной нагрузкой. Эта возможная (виртуальная) работа равна произведению единичной нагрузки на перемещение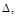 
которое совершает точка её приложения; таким образом:
Авнш=1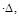 
Где величина 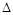представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.
|
|
|
Возможная работа внутренних сил представляет собой работу, совершаемую этими силами (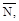 
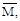
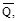
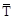) при возможной деформации элементов конструкции. Эти деформации выбираем такими же, как и действительные деформации, возникающие при действии на конструкцию реальных нагрузок. Обозначая эти деформации через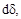 
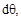
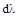и 
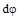(рис. 2 при растяжении (а), изгибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:
Ивнт=∫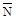 
+∫ 
+∫ 
+∫ 
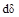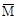
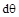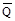
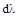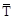
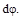
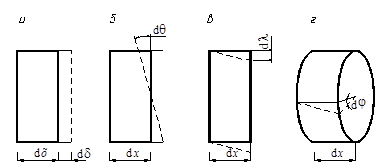
Рис. 2
Приравняв, выражение для работ внешних и внутренних сил получаем:
=∫ +∫ +∫ +∫
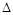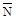
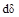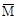
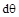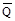
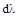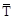
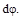
Если деформации малые упругие (справедлив закон Гука), а внутренние усилия в первой системе реальных нагрузок обозначить через NF, MF, QF и TF, то деформации элемента можно записать:
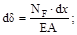
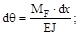
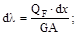
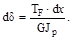
Первое из этих выражений даёт удлинения элемента при действии нормальной силы NF, а последующие деформации при изгибе, сдвиге и круче-нии.
В окончательном виде метод Мора имеет вид
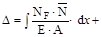
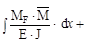
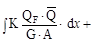
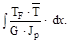
Входящий в формулу К- числовой коэффициент, зависящий от формы поперечного сечения бруса.
Порядок определения перемещений можно кратко изложить следующим образом:
1) разделив конструкцию на участки записываем аналитические выражения для внутренних силовых факторов, на каждом участке, вызванных системой реальных нагрузок- NF, MF, QF, TF;
2) в точке, перемещение которой хотим определить, в направлении искомого перемещения приложим единичную нагрузку и определяем внутренние силовые факторы, возникающие в поперечных сечениях, только от этой единичной нагрузки (и возникших реакций). При этом необходимо, чтобы правила знаков и направление обхода участков в п.п 1и 2 были бы те же самые.
3) подставить найденные значения в интегралы Мора и выполнить интегрирование по всей конструкции и просуммировать результаты для получения величины перемещения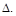 
Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направлению единичной нагрузки.
Не все члены интегралов Мора могут понадобиться. Так при расчёте ферм только слагаемые, содержащие нормальные силы необходимо учитывать, а для балки или плоской рамы существенными будут только деформации изгиба и уравнение упрощается:
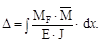
Такие интегралы можно вычислить для каждого элемента конструкции (участка), а затем просуммировать полученные результаты.
При вычислении интеграла Мора, как правило, рассматриваются такие элементы конструкций в которых жёсткости (EA, EJ, GJр) остаются постоянными. Следовательно их можно вынести из под интегралов, после чего все подинтегральные члены уравнения имеют форму произведений, скажем:
∫ МF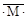 
dx.
В 1925 г. студент Московского института железнодорожного транспорта А.Н. Верещагин предложил упрощение вычислений с использованием формулы Мора для стержневых систем, состоящих из прямых участков с постоянной (в пределах каждого участка) жёсткостью. Упрощение базируется на том, что эпюры от единичных нагрузок оказываются линейными.
Допустим, на участке длинной l нужно взять интеграл.
J=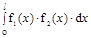 
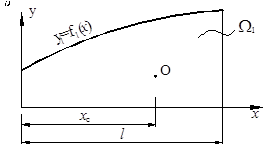
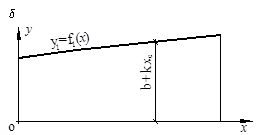
Рис. 3 .
при условии, что f2(x)- линейная функция.
f2(x)=b+kx.
Тогда:
J=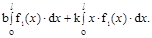 
Первый из интегралов представляет собой площадь, ограниченную кривой f1(x) (рис. 3 а), которую обозначим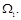 
Второй интеграл представляет собой статический момент этой площади относительно оси y, т.е.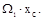 
где хс- координата центра тяжести первой эпюры
Итак, J=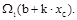 
Так как b+kxc=f2(xc) (рис. 12.3 б), то
J=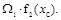 
Операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.
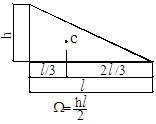
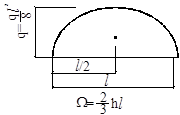Встречающиеся на практике эпюры могут быть расслоены на простейшие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.
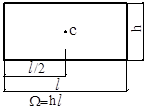
Рис.12.4
Определение перемещений от симметричного и обратно симметричного воздействия надо вести раздельно, проводя вычисления только для половины
системы. Из свойства её симметрии вытекает важное правило: если при “перемножении” эпюр одна из них симметрична, а другая обратно симметрична, то их “ произведение”(премещение)равно нулю.
Если жёсткость стержня переменная, то эпюру усилий от внешних воз-действий надо привести к одной жёсткости, умножая её ординаты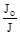 
, где Jo- момент инерции одного из сечений.
Канонические уравнения
Основная система с заданной нагрузкой и лишними неизвестными, эквивалентна заданной статически неопределимой системе. Следовательно, перемещения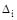 
по направлению каждой неизвестных сил Хi от заданной нагрузки и всех неизвестных усилий в лишних связях должны равняться нулю.
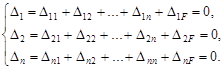
Для линейно деформируемых систем перемещение пропорционально силе, его вызвавшей.
Тогда:
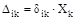
где: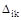 
- перемещение в направлении i-той силы, вызванное к-той силой; 
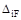-то же от внешней нагрузки; 
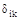- перемещение в основной системе, соответствующее силе Хi при действии силы Хк=1:
с учётом сказанного
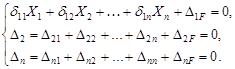
Уравнения имеют стационарную (каноническую) форму, одинаковую для всех статически неопределимых систем.
Представленная система канонических уравнений метода сил содержит главные коэффициенты при неизвестных (с одинаковыми индексами) и побочные (с разными индексами), при этом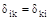 
. Величины 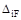называют свободными членами канонических уравнений.
Коэффициенты при неизвестных и свободные члены уравнений определяют по интегралам Мора, а в частных случаях- по правилу Верещагина. Предварительно должны быть построены эпюры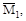 
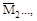
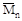от единичных нагрузок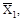 
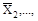
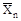и эпюры MF от заданной нагрузки.
Главные коэффициенты δii всегда положительны. Побочные же коэффициенты (перемещения) δiк могут быть положительными, отрицательными или равными нулю.
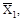
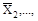
Коэффициенты и свободные члены подлежат проверке. Универсальная проверка всех коэффициентов при неизвестных состоит, в том что сумма Σδii+ 2Σδiк, представляющая собой условное перемещение по направлению всех неизвестных от всех единичных сил 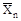, должна быть равна величине
δss=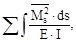 
где: Ms=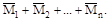 
Чтобы возможные ошибки, допущенные при построении единичных эпюр, не перенесли на эпюру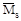 
и не свести тем самым на нет всю проверку, следует строить эпюру 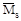независимо от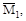 
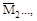
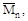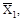
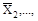
т.е. непосредственно от единичных сил 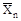, действующих на основную систему одновременно.
Если универсальная проверка приводит к недопустимо большому расхождению между суммой контролируемых перемещений и условным перемещением, то для нахождения ошибки можно произвести построчные проверки, которые состоят в том, что сумма коэффициентов при неизвестных каждого уравнения δi1+δi2+…+δin должна быть равна величине:
δis=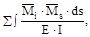 
Если построчные проверки дают расхождения только в одной строке, то ошибка связана с вычислением главного коэффициента этой строки. Если же расхождения наблюдаются одновременно в двух строках, то ошибка скорее всего допущена при вычислении того побочного коэффициента, который входит в обе строки.
Проверка свободных членов уравнений состоит в том, что их сумма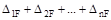 
должна быть равна величине
ΔsF =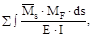 
После проверки коэффициентов при неизвестных и свободных членов
канонических уравнений производят их решение и находят .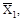
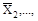
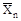Построение эпюр внутренних усилий
Для построения эпюры моментов в статически определимой системе можно использовать зависимость:
М=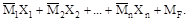 
Существует так называемая кинематическая проверка, состоящая в проверке равенства нулю условного перемещения основной, или, что то же, заданной системы по направлению всех неизвестных от всех неизвестных и заданной нагрузки, т.е.
ΔS =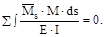 
Должны выполнятся и отдельные условия:
Δi =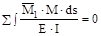 
(i=1,2…,n).
Эти условия называют деформационной проверкой, суть которой состоит в том, что перемножают окончательную эпюру изгибающих моментов Mz и одну из единичных эпюр изгибающих моментов Mi, определяя при этом перемещение в i-той лишней связи, зная, что оно должно быть равным нулю.
Эпюры поперечных сил Q и продольных сил N строятся для основной системы с заданной нагрузкой и вычисленными неизвестными. В то же время для построения эпюры Q можно использовать заданную нагрузку и эпюру М и рассматривать равновесие отдельных стержней. Для построения эпюры N можно использовать заданную нагрузку и эпюру Q и рассматривать равновесие узлов.
Проверка эпюр Q и N состоит в том, что для любой отсечённой части рамы суммы проекций на две оси внешних и внутренних сил должна равняться нулю (статическая проверка).
Для определения перемещения любой точки статически неопределимой системы достаточно образовать основную систему и в точке, перемещение которой необходимо определить, приложить единичную нагрузку в направлении искомого перемещения. Построив эпюру изгибающих моментов от этого воздействия в любой основной системе, следует перемножить её с окончательной эпюрой изгибающих моментов статически неопределимой системы. Если перемещение получено со знаком “минус”, то действительное направление перемещения противоположно направлению единичной нагрузки.
Дата добавления: 2021-02-10; просмотров: 43; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!