Интеграл от рациональной дроби.
Неопределенный интеграл.
Определение 1. Функция F ( x ) называется первообразной для функции f ( x ) в промежутке 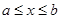 , если в любой точке этого промежутка ее производная равна f ( x ):
, если в любой точке этого промежутка ее производная равна f ( x ):
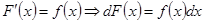 ,
, 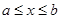 . (1)
. (1)
Определение 2. Совокупность всех первообразных функций F(x) + с для функции f ( x ) на некотором промежутке называется неопределённым интеграломи обозначается

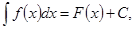 (2)
(2)
где f ( x ) dx называется подынтегральным выражением, х - переменной интегрирования, а С -произвольной постоянной интегрирования. Процесс нахождения первообразной функции называется интегрированием. Например  , т.к.
, т.к. 
Метод непосредственного интегрирования.
Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводятся к одному или нескольким табличным интегралам.
Формулы интегрирования:
1.  2.
2. 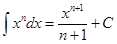
где 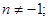
3. 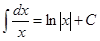 4.
4. 
5. 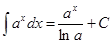 6.
6. 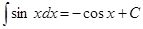
7. 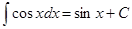 8.
8. 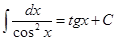
9. 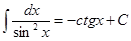 10.
10. 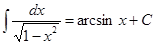
11. 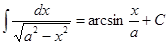 12.
12. 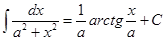
13. 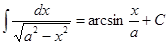 14.
14. 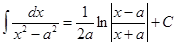
15. 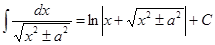
Свойства неопределённого интеграла
1) 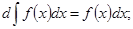 2)
2)  3)
3) 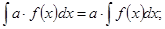

4) 
Примеры
1) 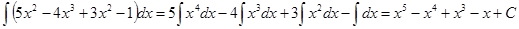
|
|
|
Проверка:
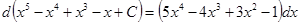
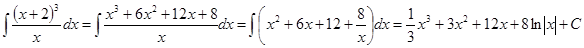
Проверка:
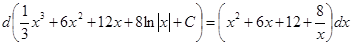
Интегрирование способом подстановки (замена переменной)
Сущность интегрирования методом подстановки заключается в преобразовании интеграла 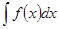 в интеграл
в интеграл 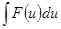 , который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения
, который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения 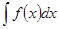 заменяем переменную х новой переменной и с помощью подстановки.
заменяем переменную х новой переменной и с помощью подстановки. 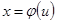 .Дифференцируя это равенство, получаем
.Дифференцируя это равенство, получаем  . Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через
. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через 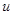
 , имеем
, имеем
 (3)
(3)
После того, как интеграл относительно новой переменной и будет найден, с помощью подстановки  он приводится к переменной х.
он приводится к переменной х.
Примеры:
l)  2)
2) 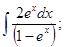
Решение:
1) положим 1 + х = z. Продифференцируем это неравенство:  или dx = dz .
или dx = dz .
Заменим в интеграле: 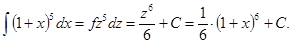
2) Сделав замену: 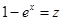 , получим
, получим 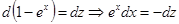 . Тогда
. Тогда
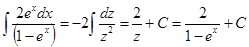
Интегрирование “по частям”
Интеграл из пункта в) вашей контрольной работы берется методом интегрирования “по частям”. Этим методом интегрируются некоторые произведения, например произведения степенной функции на логарифмическую или на показательную, или на тригонометрическую, или на обратные тригонометрические функции и др.
Интегрирование “по частям” производится по формуле
|
|
|
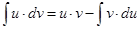
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за “u”, а оставшийся множитель вместе с dx принять за “dv”.
Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать “u” и “dv”.
В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за “u”. Если подынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за “u” принимается степенная функция.
Пример.
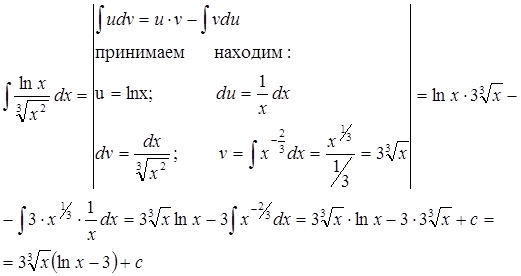

Пример.
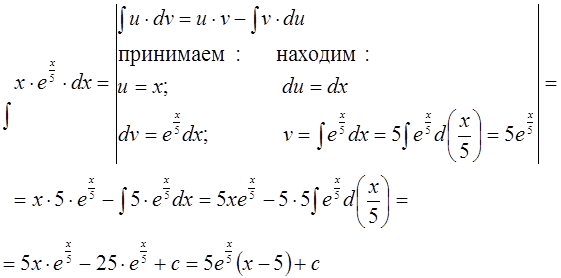
Интеграл от рациональной дроби.
В пункте г) вашей контрольной работы предлагается взять интеграл от рациональной дроби.
Пример.
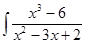
Под знаком интеграла стоит рациональная дробь.
1. Так как подинтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе),то выделим целую часть, разделив числитель на знаменатель “углом” (аналогично тому, как в задачах 41-50):
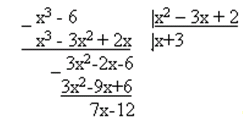
Итак, подынтегральную функцию можно записать в виде:
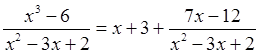
Тогда данный интеграл (обозначим его J), можно представить как сумму интегралов:
|
|
|

2. Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J1, разложим знаменатель подынтегральной функции на множители.
Для этого найдем корни квадратного трехчлена, стоящего в знаменателе: x2-3x+12=0.

Тогда
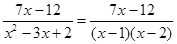
3. Представим полученную правильную дробь в виде суммы элементарных дробей:
4. 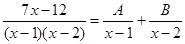 (*)
(*)
Здесь А и В - числа, которые нужно найти. Сделаем приведение к общему знаменателю в правой части:
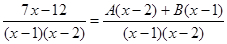
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:
7x-12=A(x-2)+B(x-1);
7x-12=Ax-2A+Bx-B;
7x-12=(A+B)x+(-2A-B).
Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х:

Получена система двух уравнений с двумя неизвестными А и В, решив которую, найдем А=5; В=2.
Подставим найденные числа в равенство (*):
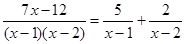
4. Вернемся к интегралу J1:

5. Окончательно искомый интеграл равен:
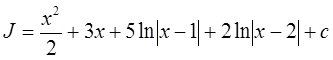
Дата добавления: 2021-02-10; просмотров: 60; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
