Числовые характеристики случайных величин. Их роль и назначение

Мы познакомились с рядом полных, исчерпывающих характеристик случайных величин - так называемых законов распределения. Перечислим их:

для дискретной случайной величины – функция распределения; – ряд распределения (графически - много угольник распределения);

для непрерывной величины – функция распределения; – плотность распределения (графически - кривая распределения).

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случайную величину с вероятностной точки зрения. На практике часто не нужно характеризовать случайную величину полностью. Достаточно бывает лишь указать только отдельные числовые параметры, каким-либо образом характеризующие существенные черты распределения случайной величины. Например, какое-то среднее значение, около которого группируются возможные значения случайной величины; какое-либо число, характеризующее степень разбросанности этих значений относительно среднего и т.д. Пользуясь такими характеристиками, мы можем все существенные сведения относительно случайной величины, которыми располагаем, выразить кратко с помощью минимального числа числовых параметров. Такие характеристики, назначение которых выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины. С помощью таких характеристик существенно облегчается решение многих вероятностных задач.

Характеристики положения (математическое ожидание, мода, медиана)

Среди числовых характеристик случайных величин отметим те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожидание случайной величины, которое иногда просто называют средним значением случайной величины.

Математическим ожиданием (средним значением) дискретной случайной величины называют сумму всех произведений значений случайной величины на соответствующие им вероятности.

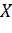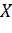Математическое ожидание случайной величины обозначают . Если  - случайная величина, то 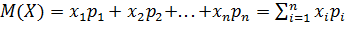, где

 

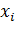
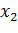
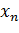
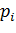
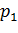
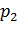
Остановимся на свойствах математического ожидания случайной величины.

1. Математическое ожидание постоянной величины равно этой постоянной.

2. Постоянный множитель можно выносить за знак математического ожидания, т.е. .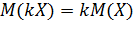

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий.

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания всегда равно нулю: .

Пусть 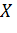– непрерывная случайная величина, которая принимает значения значения на всей числовой прямой, тогда математическое ожидание непрерывной случайной величины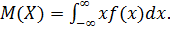

Кроме важнейшей из характеристик наложения - математического ожидания - на практике иногда применяются и другие характеристики наложения, в частности, мода и медиана случайной величины.

Модой случайной величины называется ее наиболее вероятное значение.

Часто применяется еще одна характеристика положения – медиана случайной величины. Медианой случайной величины 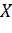называется такое ее значение , для которого 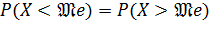, т.е. одинаково вероятно, окажется ли случайная величина меньше или больше .

 

4.2. Дисперсия случайной величины и ее свойства

Математическое ожидание случайной величины характеризует ее в среднем, это центр ее распределения. Дисперсия случайной величины есть характеристика распределения, разбросанность значений случайной величины около ее математического ожидания.

Дисперсия случайной величины – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания .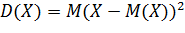

Если 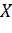 - дискретная случайная величина, которая задается как

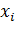
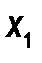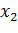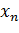
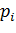
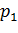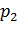
Тогда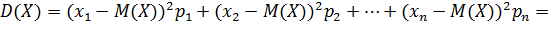  

 

Если 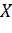 - непрерывная случайная величина с плотностью распределения , то

.

Пример1. Найти дисперсию случайной величины 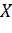 числа выпавших очков при подбрасывании игральной кости.

Решение. Здесь X = m с вероятностью p_m = 1/6, m = 1,2,3,4,5,6.

,

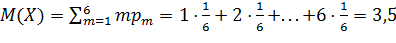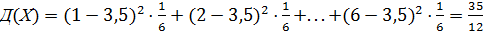
Пример 2. Найти дисперсию случайной величины 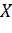, которая принимает значения только на промежутке [- 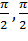] с плотностью .

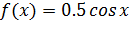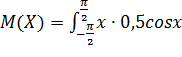
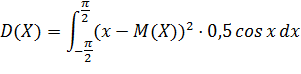
Дисперсия как мера рассеивания значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии – это квадрат размерности случайной величины). Поэтому вводится еще одна мера рассеивания с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратичное отклонение, которое определяется как корень квадратный из дисперсии. Среднее квадратичное отклонение обозначается символом  или ,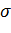  

 

Свойства дисперсии

1. Дисперсия постоянной величины всегда равна нулю, .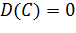

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат,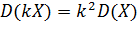

3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсий, то есть

4. Упрощенное правило вычисления дисперсии: дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания, то есть .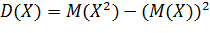

 

Задачи

1. Задают ли законы распределения дискретной случайной величины следующие таблицы?

а) 2 3 4 5 0,1 0,4 0,3 0,2

б) 6 7 8 9 0,1 0,2 0,3 0,5

2. Дискретная случайная величина 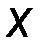имеет закон распределения

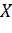
	3	4	5	6	7
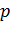
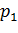
		0,15		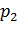0,25	0,35

Найти вероятност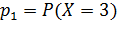и  и 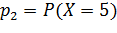, если известно, что  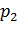в четыре раза больше .

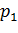3. Трижды подбрасывается монета. Случайная величина Х – число выпавших гербов. Описать закон распределения данной случайной величины. Найти функцию распределения и числовые характеристики.

4. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. В городе 4 библиотеки. Случайная величина Х – это число библиотек, которые посетит студент. Описать закон распределения данной случайной величины. Найти функцию распределения и числовые характеристики.

5. Произведено три независимых выстрела по цели. Составить ряд распределения случайной величины Х – числа попаданий в цель, если вероятность попадания равна 0,8.

6. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. Найти закон распределения случайной величины Х, равной числу красных карандашей в выборке.

7. Найти интегральную функцию распределения, если задана дифференциальная функция.

8. Найти дифференциальную функцию распределения, если задана интегральная функция  и вычислить

.

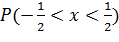9. Найти математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей

	3	4	5	6	7
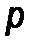
	0,1	0,2	0,4	0,2	0,1

11. Известны математические ожидания двух случайных величин М(Х) = 3 и М(У)= 2. Найти математические ожидания суммы и разности этих величин.

12. Известны математические ожидания двух независимых случайных величин М(Х)=4 и М(У)=5. Найти математическое ожидание их произведения.

13. Найти математическое ожидание и дисперсию случайной величины, если задана дифференциальная функция распределения

.

14. Найти математическое ожидание и дисперсию, если задана плотность распределения

.

15. Дана плотность распределения f ( x ) непрерывной случайной величины. Найти константу С и вычислить математическое ожидание, дисперсию и среднеквадратичное отклонение. Плотность распределения задается следующим образом:

.

16. Закон распределения дискретной случайной величины Х задан таблицей

x	-2	-1	0	1	2
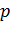
	0,1	0,2	0,4	0,2	0,1

17. Вычислить дисперсию этой случайной величины двумя способами.

18. Дискретная случайная величина Х имеет закон распределения

	1	2	3	4	5
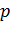
	0,1	0,2	0,4	0,2	0,1

Записать закон распределения случайной величины .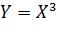

19. Дискретная величина задана законом распределения

	-2	-1	0	1	2
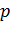
	0,1	0,2	0,15	0,25	0,3

Найти закон распределения случайной величины .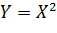

 

---

Дата добавления: 2021-02-10; просмотров: 106; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!