Метод Сімпсона (метод парабол або метод криволінійних трапецій)

Міністерство освіти і науки України

Вінницький національний технічний університет

Інститут автоматики, електроніки та комп’ютерних

Систем управління

Факультет АКСУ

Кафедра АІВТ

 

Курсова робота

З дисципліни

«Обчислювальні методи та застосування ЕОМ»

Дослідження методів чисельного інтегрування

 

 

2006

Анотація

 

В даній курсовій роботі розроблена програма для обчислення визначеного інтегралу методом Чебишева третього четвертого та п’ятого порядків.

Програма дозволяє отримати розв’язання інтегралу зазначеним методом, оцінити похибки та порівнювати їх з точним обчисленнями отриманими в математичному пакеті Mathcad 2001 Professional.

 

Теоретичні відомості

 

У курсовій роботі проведено дослідження методів чисельного інтегрування. Адже, у задачах, пов'язаних з аналізом, ідентифікацією, оцінкою якості, моделюванням різноманітних пристроїв автоматики, керування, інформаційно-вимірювальної техніки, радіоелектроніки, виникає необхідність обчислення визначених інтегралів.

В основу чисельного інтегрування покладено наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла:

 

 

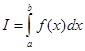
Загальний підхід до розв’язування цієї задачі такий: визначений інтеграл I являє собою площину, обмежену кривою f(х), віссю Х та прямими Х = a, Х =b, відрізок від a до b розбивають на множину менших відрізків, знаходять наближено площу кожної площини Si, яку отримують за таким розбиванням, значення інтеграла І знаходять як суму площ площин Sі, тобто I = 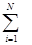Si. При цьому використовують два способи розбивання початкового відрізка на менші

1.Розбивання відрізка проводиться раніше, до того ж завжди відрізок вибирають рівним (метод прямокутників, трапецій, Сімпсона).

2.Місцезнаходження та довжина відрізків визначаються аналізом, до того ж спочатку ставиться за мету досягти найбільшої точності з заданим числом відрізків, а потім відповідно з цим визначають їхні межі (методи Гаусса, Ньютона - Котеса, Чебишева) [1].

Метод прямокутників

 

Найпростішим методом наближеного обчислення інтеграла є метод прямокутників, геометрична інтерпретація якого зводиться до знаходження визначеного інтеграла як суми площ N прямокутників (з висотою f(x) та основою h= 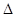x_i=x_i+1-x_i), отриманих розділень відрізка[a,b] на N рівних частин, до того ж якщо розділити на прямокутники зліва на право, то отримаємо формулу лівих прямокутників:

 

I_n= 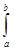f(x)dx» 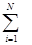S_i=h[f(x₀)+f(x₁)+...+f(x_n-1)]=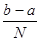 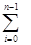f(x_i);(1.1)

 

якщо ж розділити на N прямокутників справа на ліво, то отримаємо формулу правих прямокутників:

 

I_пр= 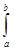f(x)dx»h[f(x_n)+...+f(x₁)]=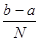 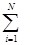f(x_i)(1.2)

Метод трапецій

 

Суть методу трапеції, полягає в тому, що інтеграл обчислюється по-іншому, відрізок інтегрування поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково- лінійною функцією j(x), отриманою стягуванням ординат N відрізків хордами.

Обчислення визначеного інтеграла зводиться до знаходження сум площ S_i прямокутних трапецій N.

Площа кожної такої трапеції визначається як:

 

S_i=h 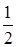(f(x_i)+f(x_i+1)).(1.3)

Отже, формула трапеції:

 

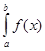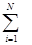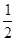I= » S_i=h( f(x₀)+f(x₁)+f(x₂)+...+f(x_n-1)+ 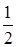f(x_N)= = 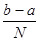[ 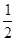(f(x₀)+f(x_n))+ 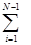f(x_i) ]. (1.4)

 

Графічна модель

 

 

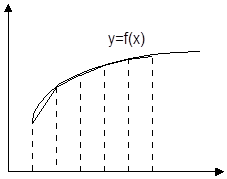
Похибка обчислення інтеграла за формулою трапецій оцінюється як

 

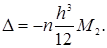(1.5)

 

Де М₂ –максимальне значення другої похідної. f(x) при 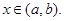,h-крок обчислень.

 

Метод Сімпсона (метод парабол або метод криволінійних трапецій)

 

Цей метод також використано у курсовій роботі, близький до методу трапецій у тій частині, що інтегрування проводиться шляхом поділу відрізка інтегрування [а, b] на множину відрізків (N пар відрізків). Однак, з метою збільшення точності наближеного інтегрування на кожному відрізку [Xi, Xi+2] підінтегральної функції f(x) замінюють квадратичною параболою j(x), обчислення визначеного інтеграла зводиться до обчислення суми N криволінійних трапецій Si: I= 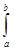f(x)dx» 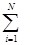Si [1].

 

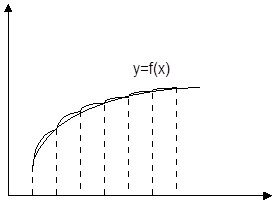Графічна модель.

 

Площа кожної такої трапеції визначається за формулою Сімпсона:

 

Si= 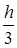 [f(xi)+4f( xi+1)+f(xi+2)], (1.6), тобто

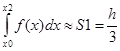(y₀+4y₁+y₂),

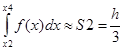(y₂+4y₃+y₄),

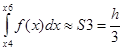(y₄+4y₅+y₆), (1.7)

. . . . . . . . . . . . . . . . . . . . . . .

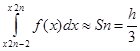(y_2n-2+4y_2n-1+y_2n),

 

Тоді чисельне значення визначеного інтеграла на відрізку [a,b] дорівнюватиме сумі інтегралів, тобто

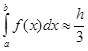[y₀+y_2n+4(y₁+...+y_2n-1)+2(y₂+...+y_2n-2)],

 

або

 

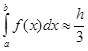[y₀+y_2n+4 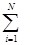y_2i-1+2 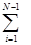y_2i],(1.8)

 

де h =(b-a)/2N.

Похибка обчислення інтеграла за формулою Сімпсона оцінюється як

 

 

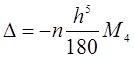
де М₄ –максимальне значення четвертої похідної. f(x) при 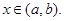, h-крок обчислень.

 

Метод Ньютона-Котеса

 

Цей метод засновано на апроксимації однієї із сторін криволінійної трапеції, яка отримується поділом відрізка [a,b] на N рівних частин, многочленами вищих порядків, також як у методі трапецій використовується лінійна апроксимація (заміна однієї із сторін трапеції прямою лінією), а в методі Сімпсона - апроксимація параболою.

Основна формула методу:

 

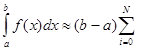y_iH_i,(1.9)

 

де Hi - коефіцієнти Ньютона - Котеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки N (кількість вузлів інтерполяцїї). Таким чином, коефіцієнти Ньютона - Котеса можна обчислити раніше для різного числа вузлів інтерполяції .

Легко можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона - Котеса.

 

Метод Чебишева

 

Метод Чебишева використано в курсовій грунтується на обчисленні інтеграла за значеннями функції yi =f(xi),(i=1,2,...,N) у зафіксованих вузлах інтерполяції x1,x2,...,xN (де h=const). Коефіцієнти Ньютона -Котеса Нi (i=1,N) не залежать від значень функції у вузлах інтерполяції. П.Л.Чебишев запропонував для обчислення визначених інтегралів використати формулу:

 

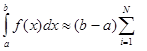c_if(x_i)_,(1.10)

 

в якій квадратурні коефіцієнти сi (i = 1,2, ...,N) зафіксовані, а абсциси xi (i=1,2,...,N)підлягаютьвизначенню.

 

Таблиця 1.1.

Коефіцієнти Ньютона - Котеса

n = 1	Но = H1 = ½
n = 2	Но = Н2 = 1/6, Н1 = 2/3
n = 3	Н0 = Н3 = 1/8, Н1 = H2 = 3/8
n = 4	Но = Н4 = 7/90, Н1 = Нз = 16/45, Н2 = 2/15
n = 5	Н0 = Н5 =19/288, Н1 = Н4 = 25/96, Н2 = Нз = = 25/144
n = 6	Но = Н6 = 41/840, Н1 = Н5 = 9/35, Н2 = Н4 = =9/280, Нз = 34/105
n = 7	Но = Н7 = 75І/17280, Н1 = Н6 = 3577/1728О, Н2 = Н5 =1323/1728О, Нз = Н4 = 2989/17280

 

Для простоти обчислень необхідно вибрати С1=...=Сn. Розглядаємо спочатку частинний випадок, коли межі інтегрування дорівнюють -1 та 1. Тоді формула Чебишева набере вигляду:

 

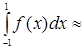2Cn[f(x₁)+f(x₂)+...+f(x_n)],(1.11)

 

де квадратурні коефіцієнти Сn та абсциси xi підлягають визначенню.

Коефіцієнти та вузли інтерполяції xi визначимо із умови, що ця рівність є точною для випадку, коли f(х) многочлен вигляду:

 

f(x)=a₀+a₁x+a₂x²+...+a_nxⁿ.(1.12)

 

Підставимо многочлен у ліву частину попередньої формули та про- інтегруємо:

 

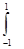(a₀+a₁x+a₂x²+...+a_nxⁿ)=2(a₀+ 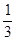a₂+ 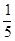a₃+...).(1.13)

 

У праву частину рівності (1. 11) підставимо значення многочлена (1.І2) у вузлах x1,x2,...,xn:

 

f(x₁)=a₀+a₁x₁+a₂x₁²+a₃x₁³+...+a_nx₁ⁿ,

f(x₂)=a₀+a₁x₂+a₂x₂²+a₃x₂³+...+a_nx₂ⁿ,

f(x₃)=a₀+a₁x₃+a₂x₃²+a₃x₃³+...+a_nx₃ⁿ,(1.14)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

f(x_n)=a₀+a₁x_n+a₂x_n²+a₃x_n³+...+a_nx_nⁿ,

Тоді рівність (1.ІЗ) набере вигляду:

 

2(a₀+ 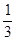a₂+ 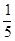a₄+...)=2c_n[na₀+a₁(x₁+x₂+...+x_n)+a₂(x₁²+x₂²+...+x_n²)+

+a₃(x₁³+x₂³+...+x_n³)+...+a_n(x₁ⁿ+x₂ⁿ+...+x_nⁿ)].(1.15)

 

Отримана рівність повинна виконуватися за будь-яких значень a₀,a₁,...,a_n; таким чином, порівнюючи коефіцієнти аi в правій та лівій частинах (1.І5) знаходимо, що nсn = 1, звідки

 

C_n= 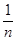.(1.16)

 

і, крім цього,

 

x₁+x₂+x₃+...+x_n=0,

x₁²+x₂²+x₃²+...+x_n²= ,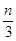

x₁³+x₂³+x₃³+...+x_n³=0,(1.17)

x₁⁴+x₂⁴+x₃⁴+...+x_n⁴= ,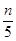

. . . . . . . . . . . . . . . . . . .

x₁ⁿ+x₂ⁿ+x₃ⁿ+...+x_nⁿ= 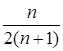[1-(-1)ⁿ⁺¹],

 

Підставляючи знайдене для С_n виразу в співвідношені 1.13 отримаємо формулу Чебишева:

 

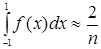[f(x₁)+f(x₂)+...+f(x_n)],(1.18)

 

де точки x1,...,хn визначаються із системи рівнянь (1.17).

Значення x1,...,хn для різних n обчислюються раніше та зводять в табл. 1.2.

Коли межі даного інтеграла відрізняються від -1 та 1, формула Чебишева матиме вигляд:

 

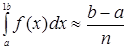[f(z₁)+f(z₂)+...+f(z_n)],(1.19)

де

 

Таблиця 1.2.

Число ординат	Значення абсцис
n = 2 n = 3 n = 4 n = 5 n = 6 n = 7	-x1 = x2 = 0.577350 -x1 = x3 = 0.707107; x2 = 0 -x1 = x4 = 0.794654; -x2 = x3 = 0.187592 -x1 = x5 = 0.832498; -x2 = x4 = 0.374541; х3 = 0 -x1 = x6 = 0.866247; -x2 = x5 = 0.4225І9; -x3 = x4 = 0.266635 -x1 = x7 = 0.883862; -x2 = x6 = 0.529657; -x3= = x5 = 0.323912; x4 = 0

 

Z_i= 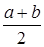+ 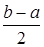x_i, (i=1,2,...,n),(1.20)

 

а xi мають вкaзані в таблиці значення.

Похибка обчислень за методом Чебишева знаходиться за формулою:

 

 

---

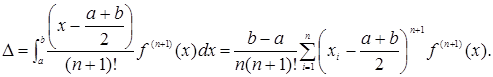
Дата добавления: 2021-02-10; просмотров: 114; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!