Поток через различные сечения векторной трубки сохраняет постоянное значение.
В гидромеханической интерпретации – при отсутствии источников количество жидкости, протекающей через различные сечения векторной трубки, сохраняет постоянное значение.
Циркуляция. Ротор.
Рассмотрим векторное поле
F(P) = X(x,y,z) i + Y(x,y,z) j + Z(x,y,z) k (1)
и замкнутый контур (L).


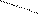

 F( P) dr
F( P) dr
Fs (L)

 P
P
Рассмотрим интеграл
 - циркуляция вектора F вдоль замкнутого контура ( L).
- циркуляция вектора F вдоль замкнутого контура ( L).
Дадим другое выражение циркуляции. Рассмотрим векторdr = {dx, dy, dz}. Тогда

Циркуляция запишется
Ц = 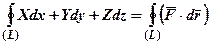 .
.
Физический смысл циркуляции. Если поле силовое, то циркуляция равна работе поля вдоль замкнутого контура (L).
Формула Стокса для контура (L) имеет вид
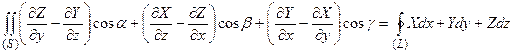
Здесь (S) – поверхность, натянутая на контур (L).

 n0
n0
(S)

(L)
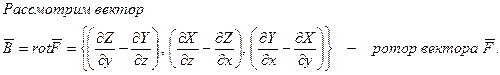
Поле вектора F порождает другое векторное поле – поле ротора.
Формула Стокса в векторном виде запишется
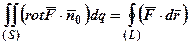 .
.
 Поток ротора через поверхность ( S), натянутую на замкнутый контур ( L), равен циркуляции вектора F вдоль этого контура.
Поток ротора через поверхность ( S), натянутую на замкнутый контур ( L), равен циркуляции вектора F вдоль этого контура.
Направление обхода контура( L) должно быть согласовано с выбранным направлением нормали n0, Если смотреть с конца вектора n0, обход контура ( L) должен казаться происходящим против часовой стрелки.
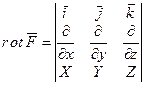
Если для данного векторного поля rot F = 0, то
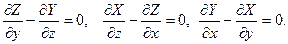 = 0, но это означает, что существует функция u = u(x, y, z) такая, что du = X dx + Y dy + Z d z . Отсюда
= 0, но это означает, что существует функция u = u(x, y, z) такая, что du = X dx + Y dy + Z d z . Отсюда
|
|
|

т.е. поле вектора F является полем градиента.
Функция u( x, y, z) называется потенциалом, а поле вектора F называется потенциальным.
Очевидно, rot grad u = 0.
Примеры.
1. Дана векторная функция F(x, y, z) = 20y i + 9y j + 12z k. Найти поток вектора
a) через полную поверхность пирамиды, ограниченной плоскостями координат и плоскостью (S) 12x + 3y – 4z -12 = 0 в направлении внешней нормали;
b) через грань (S).
Р е ш е н и е.
a) 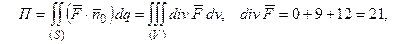
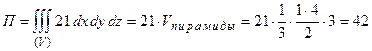

 z
z



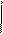

 k dq
k dq


 B y γ
B y γ





 A
A
 x dx dy
x dx dy
n0
C
b) 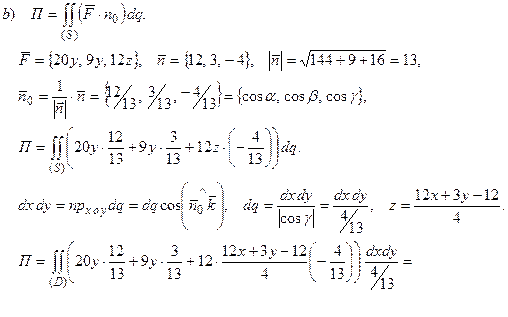



y
 y = 4 – 4x
y = 4 – 4x
(D)
0 1 x
|
|
|
2. В условиях предыдущей задачи найти циркуляцию векторного поля F(x, y, z) вдоль линии пересечения плоскости (S) с координатными плоскостями двумя способами
a) по формуле Стокса, приняв в качестве поверхности, по которой производится интегрирование, плоскость треугольника, отсекаемого от плоскости (S) координатными плоскостями, при этом считать нормаль направленной в сторону противоположную началу координат;
b) непосредственно, по определению циркуляции.
Решение.
a)
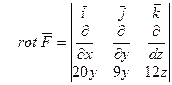 = − 20 k.
= − 20 k.
По формуле Стокса
 ∙
∙ 
c) Непосредственно, по определению циркуляции.
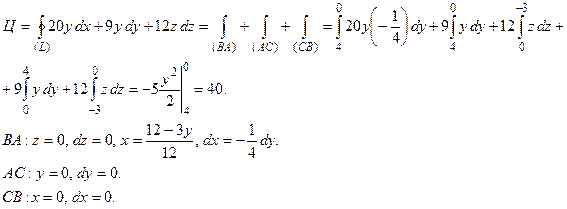
Оператор Гамильтона (1805−65, Англия).
Известно, что со скалярным полем u = u(x, y, z) связывается векторное поле – поле градиента
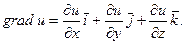
С векторным полем F(x, y, z) = 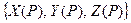 связывается скалярное поле – поле дивергенции и векторное поле ротора.
связывается скалярное поле – поле дивергенции и векторное поле ротора.
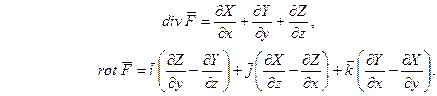
Гамильтон заметил, что все эти операции могут быть записаны более просто, если ввести символ

Это − знак действия над полем, т.е. оператор. Этот оператор обладает как свойствами вектора, так и свойствами оператора дифференцирования.
«Умножение» т.е. воздействие оператора на скалярное поле u и на векторное поле F производится по следующим правилам
|
|
|
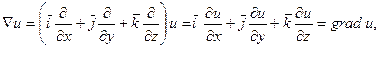
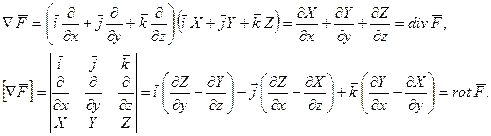
При действиях с оператором  следует пользоваться правилами векторной алгебры и правилами дифференцирования. Например.
следует пользоваться правилами векторной алгебры и правилами дифференцирования. Например.

После применения оператора 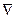 к полю получается новое поле (скалярное или векторное), на которое можно вновь воздействовать оператором
к полю получается новое поле (скалярное или векторное), на которое можно вновь воздействовать оператором 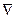 . Повторное применение операции
. Повторное применение операции 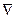 называется операцией второго порядка. Не все операции второго порядка имеют смысл. Например, не имеет смысла операция div(div F).
называется операцией второго порядка. Не все операции второго порядка имеют смысл. Например, не имеет смысла операция div(div F).
С помощью комбинаций операций grad, div и rot можно ввести пять операций второго порядка: div( grad u), rot( grad u), grad( divF), div( rotF), rot( rotF).
rot(grad u)= [ 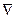 ∙
∙ 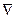 u] = 0,
u] = 0,
div(gradu)= 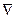 (
( 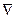 u) =
u) = 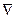 2u =
2u = 
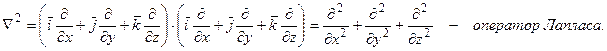
Дата добавления: 2020-12-12; просмотров: 72; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
