Проекція вектора на вісь. Координати вектора
Основи векторної алгебри
Поняття вектора
Розрізняють два види величин: скалярні і векторні.
Якщо деяка величина повністю визначається певним чином, то її називають скалярною. Прикладами скалярних величин є маса, довжина, об’єм, площа, кількість, температура та ін. Скалярні величини є алгебраїчними величинами і з ними можна здійснювати будь-які алгебраїчні дії: додавання, віднімання, множення, ділення, піднесення у ступінь.
Якщо при визначенні деякої величини крім числового значення треба знати і її напрямок, то така величина називається векторною. Прикладами таких величин є швидкість, прискорення, сила. Векторні величини зображуються за допомогою векторів.
Вектором називають спрямований відрізок, що має певну довжину, у якої одна з точок, що його обмежує, приймається за початок, а друга – за кінець. Якщо точка А – початок вектора, а точка В – його кінець, то вектор позначається символом 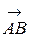 і зображують його так
і зображують його так

Вектор можна позначити й однією буквою, наприклад, 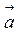 . Тоді його зображення має вигляд
. Тоді його зображення має вигляд
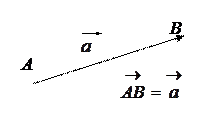
Довжина вектора 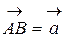 називається його модулем і позначається символом
називається його модулем і позначається символом 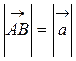 .
.
Вектор називається нульовим, якщо його модуль дорівнює нулю. У такому векторі початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, його довжина дорівнює нулю, і позначається  . Вектор
. Вектор 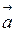 , модуль якого дорівнює 1, називається одиничним. Вектори, які лежать на паралельних прямих чи на тій же прямій, називаються колінеарними. Наприклад, колінеарними є вектори
, модуль якого дорівнює 1, називається одиничним. Вектори, які лежать на паралельних прямих чи на тій же прямій, називаються колінеарними. Наприклад, колінеарними є вектори 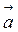 ,
, 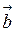 ,
, 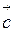 ,
,  , що подані на малюнку.
, що подані на малюнку.
|
|
|
Колінеарні вектори, які мають однаковий напрямок, називаються рівно спрямованими, а ті, що мають протилежні напрямки, – протилежно спрямованими.
Два вектори 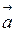 і
і  називаються рівними, якщо
називаються рівними, якщо
- рівні їхні модулі 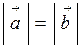 ;
;
- вони є рівно спрямованими.
У цьому разі пишуть 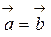 .
.
Два вектори 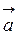 і
і  називаються протилежними, якщо:
називаються протилежними, якщо:
- рівні їхні модулі  ;
;
- вони є протилежно спрямованими.
У цьому разі пишуть 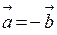 . Цілком зрозуміло, що
. Цілком зрозуміло, що 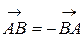 .
.
Лінійні операції над векторами.
Лінійними операціями над векторами є операції додавання, віднімання векторів і множення вектора на число.
Додавання векторів.
Сумою двох векторів 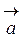 і
і 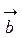 називають третій вектор
називають третій вектор 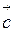 , який визначається відповідно до одного з правил:
, який визначається відповідно до одного з правил:
Правило трикутника:
1) від довільної точки О відкладаємо вектор 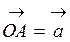 ;
;
2) від його кінця A відкладаємо вектор 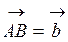 ;
;
3) початок першого вектора з’єднується з кінцем другого;
Одержаний вектор  є вектором
є вектором  , який дорівнює
, який дорівнює 
 |

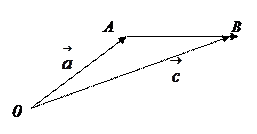
Правило паралелограма.
1) від довільної точки О відкладаємо вектор  ;
;
|
|
|
2) від тієї ж точки відкладаємо вектор 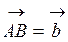 ;
;
3) побудуємо на цих векторах як на сторонах паралелограма OACB діагональ OC ;
4) вектор 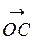 , що є діагоналлю цього паралелограма, є вектор
, що є діагоналлю цього паралелограма, є вектор 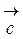 , який є сумою векторів
, який є сумою векторів 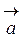 і
і 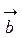 :
:  .
.

Властивості суми векторів :
1. Сума двох векторів має комутативну (переставну) властивість:
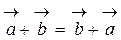 ;
;
2. Сума векторів 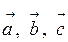 має асоціативну (поєднувальну) властивість:
має асоціативну (поєднувальну) властивість:
 .
.
Поняття суми векторів можна узагальнити на випадок довільної скінченої кількості векторів.
Сумою n векторів 
 називають вектор, початок якого збігається з початком вектора
називають вектор, початок якого збігається з початком вектора  , а кінець - з кінцем вектора
, а кінець - з кінцем вектора  за умови, що точка прикладання кожного наступного вектора збігається з кінцем попереднього. Наприклад, сумою векторів
за умови, що точка прикладання кожного наступного вектора збігається з кінцем попереднього. Наприклад, сумою векторів  є вектор
є вектор 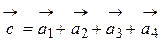
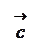
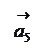
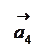
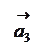


Віднімання векторів.
Різницею двох векторів 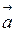 і
і 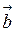 називають третій вектор
називають третій вектор 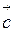 , який під час додавання з вектором
, який під час додавання з вектором 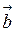 дає вектор
дає вектор 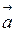 . Побудувати вектор
. Побудувати вектор 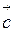 можна за малюнком
можна за малюнком
|
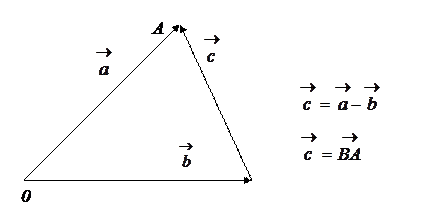
Множення вектора на число.
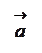 Добутком вектора
Добутком вектора 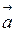 на число λ називається вектор
на число λ називається вектор  , модуль якого дорівнює модулю вектора
, модуль якого дорівнює модулю вектора 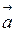 , помноженого на λ, тобто
, помноженого на λ, тобто  , а напрямок збігається з напрямком вектора
, а напрямок збігається з напрямком вектора 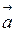 при λ > 0 і протилежний йомупри λ < 0. Наприклад, вектори
при λ > 0 і протилежний йомупри λ < 0. Наприклад, вектори 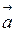 , 3
, 3 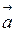 , -2
, -2 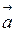 мають вигляд
мають вигляд
|
|
|
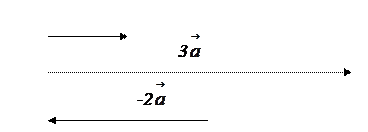
Два вектори 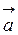 і
і 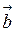 є колінеарними, якщо існують такі числа α і β, що має місце рівність
є колінеарними, якщо існують такі числа α і β, що має місце рівність 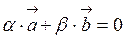 .
.
Проекція вектора на вісь. Координати вектора
Віссю називається спрямована пряма. Напрямок прямої на малюнку зазвичай позначають стрілкою. Заданий напрямок вісі вважається позитивним, протилежний до нього – від'ємним. Вісь Ох однозначно визначається одиничним вектором 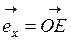 , (
, ( 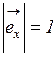 ), напрямок якого зібгається з напрямком вісі Ох.
), напрямок якого зібгається з напрямком вісі Ох.

Такий вектор 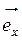 називається ортом вісі Ох.
називається ортом вісі Ох.
Кутом між вектором 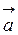 і віссю Ох називається кут φ між векторами
і віссю Ох називається кут φ між векторами 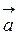 і
і 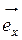 .
.
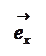

Проекцією точки А на вісь Ох називається точка А1 перетину цієї вісі з площиною, яка проходить через дану точку А перпендикулярно вісі Ох.

Проекцією вектора 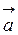 на вісь Ох називається алгебраїчна величина відрізка А1В1, де А 1, В1 – проекції точок А і В на дану вісь. Довжина відрізка А 1В1 береться зі знаком +, якщо напрямок відрізка збігається з позитивним напрямком осі Ох і зі знаком – у протилежному випадку. Відповідно до малюнка
на вісь Ох називається алгебраїчна величина відрізка А1В1, де А 1, В1 – проекції точок А і В на дану вісь. Довжина відрізка А 1В1 береться зі знаком +, якщо напрямок відрізка збігається з позитивним напрямком осі Ох і зі знаком – у протилежному випадку. Відповідно до малюнка
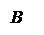
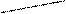


проекція вектора  на вісь ОХ є додатною величиною і визначається довжиною відрізка А1В1. Проекція вектора
на вісь ОХ є додатною величиною і визначається довжиною відрізка А1В1. Проекція вектора  на вісь О x є від’ємною величиною і дорівнює - С1D1.
на вісь О x є від’ємною величиною і дорівнює - С1D1.
|
|
|
Проекція вектора 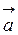 на вісь Ох дорівнює добутку його модуля на косинус кута φ між цим вектором і віссю Ох .
на вісь Ох дорівнює добутку його модуля на косинус кута φ між цим вектором і віссю Ох .
 прх
прх 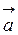 = ах =
= ах = 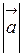 соs φ.
соs φ.
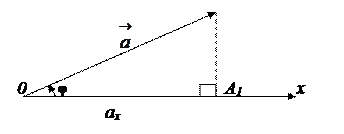
Звідси випливає, що проекція вектора на вісь додатна, якщо вектор утворює з віссю гострий кут; від’ємна, якщо цей кут тупий, дорівнює нулю, якщо цей кут прямий.
Проекції рівних векторів на ту саму вісь рівні між собою.
Проекції векторів 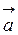 і
і 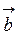 на дану вісь мають такі властивості:
на дану вісь мають такі властивості:
1. прх ( 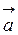 +
+ 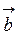 ) = прх
) = прх 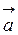 + прх
+ прх 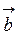 = ах + bх,
= ах + bх,
2. прх (λ ∙ 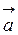 ) = λ ∙прх
) = λ ∙прх 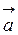 = λ ∙ах.
= λ ∙ах.
Якщо α, β, γ – кути, утворені вектором 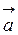 з координатними вісями Ох, Оу, Оz прямокутної системи координат, то проекції вектора
з координатними вісями Ох, Оу, Оz прямокутної системи координат, то проекції вектора 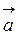 на координатні вісі визначаються за формулами
на координатні вісі визначаються за формулами
ах =  ∙соs α, ау =
∙соs α, ау =  ∙ соs β, аz=
∙ соs β, аz=  ∙ соs γ.
∙ соs γ.
Модуль вектора через його проекції на вісі прямокутної системи координат обчислюється за формулою:
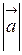 =
= 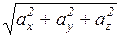 .
.
Тоді напрямні косинуси визначаємо так:
 ,
,
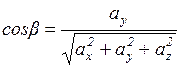 ,
,
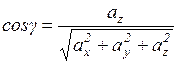 .
.
Для напрямних косинусів існує формула:
 соs2 α + соs2β + соs2 γ = 1.
соs2 α + соs2β + соs2 γ = 1.
Приклад. Вектор 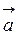 заданий координатами
заданий координатами  . Знайти модуль цього вектора і значення його напрямних косинусів.
. Знайти модуль цього вектора і значення його напрямних косинусів.
Розв’язання: Модуль вектора 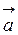 обчислюється за формулою
обчислюється за формулою  , а його напрямні косинуси дорівнюють
, а його напрямні косинуси дорівнюють 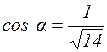 ,
, 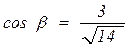 ,
,  .
.
Відповідь:  ;
;  ,
, 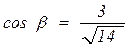 ,
,  .
.
Якщо 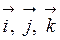 - одиничні вектори, спрямовані по координатних осях Ох, Оу, Оz відповідно, то розкладання вектора
- одиничні вектори, спрямовані по координатних осях Ох, Оу, Оz відповідно, то розкладання вектора 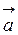 за трьома координатними осями має вигляд
за трьома координатними осями має вигляд
 ,
,
де ах, ау, аz – проекції вектора 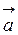 на координатні вісі Ох, Оу, Оz, які називаються координатами вектора
на координатні вісі Ох, Оу, Оz, які називаються координатами вектора 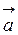 і позначаються як
і позначаються як 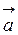 ( ах, ау, аz).
( ах, ау, аz).
Якщо початок вектора 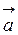 співпадає з початком координат, а його кінець- точка А - має координати х, у, z, то тоді його проекції на координатні вісі дорівнюють координатам його кінця, тобто ах = х, ау = у, аz = z.
співпадає з початком координат, а його кінець- точка А - має координати х, у, z, то тоді його проекції на координатні вісі дорівнюють координатам його кінця, тобто ах = х, ау = у, аz = z.
У цьому разі вектор 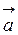 називається радіусом-вектором точки А. Радіус-вектор точки позначається зазвичай через
називається радіусом-вектором точки А. Радіус-вектор точки позначається зазвичай через 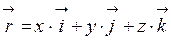 , а модуль радіуса-вектора обчислюється за формулою
, а модуль радіуса-вектора обчислюється за формулою  .
.
Якщо для вектора 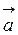 відомі координати його початку А(х1, у1, z1) і кінця В(х2, у2, z2),причому початок вектора не обов’язково збігається з початком координат, то проекції вектора
відомі координати його початку А(х1, у1, z1) і кінця В(х2, у2, z2),причому початок вектора не обов’язково збігається з початком координат, то проекції вектора 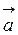 на координаті вісі визначаються таким чином
на координаті вісі визначаються таким чином
ах = х2 - х1, ау = у2 – у1, а = z2 – z1.
Вектор 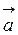 в цьому разі можна подати через його координати
в цьому разі можна подати через його координати

 ,
,
а його модуль визначається виразом
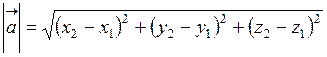 .
.
Приклад. Вектор 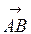 заданий координатами точок А(2, 1, 3) і В(5, -2, 3). Знайти модуль вектора
заданий координатами точок А(2, 1, 3) і В(5, -2, 3). Знайти модуль вектора 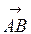 .
.
Розв’язання: Проекції вектора 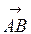 на координатні вісі дорівнюють:
на координатні вісі дорівнюють:
ах = х2 – х1 = 5 – 2 = 3,
ау = у2 – у1= -2 -1 = -3,
аz = z2 – z1= 3 – 3 = 0.
Модуль вектора 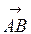 дорівнює
дорівнює 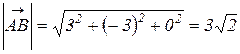 .
.
Відповідь:  .
.
Дата добавления: 2020-12-12; просмотров: 213; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
