Механический смысл векторного произведения.
Лекция 3.
1. Приложение скалярного произведения.
2. Векторное произведение векторов.
3. Механический смысл векторного произведения.
4. Векторное произведение в ортонормированном базисе.
Приложение скалярного произведения.
Напомним, что скалярное произведение векторов – это число вида
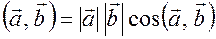 .
.
Скалярное произведение векторов, заданных в ортонормированном базисе, вычисляется по формуле
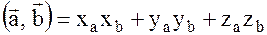 .
.
Рассмотрим следующие приложения скалярного произведения.
1). Вычисление работы.
Пусть вдоль пути 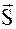 приложена сила
приложена сила 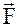 . Тогда работа этой силы равна скалярному произведению вектора силы
. Тогда работа этой силы равна скалярному произведению вектора силы 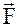 на вектор пути
на вектор пути 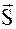 .
.
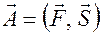
|
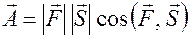 (1)
(1)
2). Нахождение длины вектора.
Модуль вектора найдём из скалярного произведения вектора самого на себя.
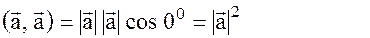
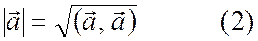 |
или
Для ортонормированного базиса: если дан вектор 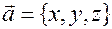 в ортонормированном базисе, то модуль вектора
в ортонормированном базисе, то модуль вектора
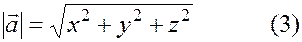
3). Нахождение угла между векторами.
Из скалярного произведения векторов 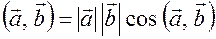 , следует, что угол между векторами вычисляется по формуле
, следует, что угол между векторами вычисляется по формуле
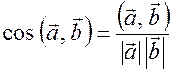 (4)
(4)
если вектора перпендикулярны 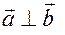 , то скалярное произведение равно нулю
, то скалярное произведение равно нулю 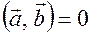 - условие перпендикулярности.
- условие перпендикулярности.
Для ортонормированного базиса условие перпендикулярности.
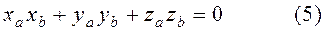 |
|
|
|
4).Нахождение проекции одного вектора на направление другого.
Из свойства 2. следует: 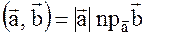 так как
так как 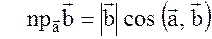 , то
, то 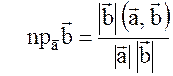 и получаем формулу для нахождения проекции вектора на вектор
и получаем формулу для нахождения проекции вектора на вектор
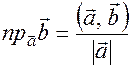 (6)
(6)
Для ортонормированного базиса
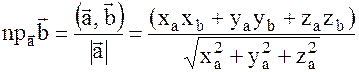 (7)
(7)
Нахождение направляющих косинусов.
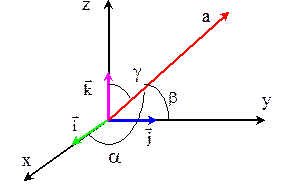 |
Определение:
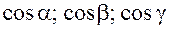 - называются направляющими косинусами вектора
- называются направляющими косинусами вектора 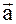 в заданной системе координат.
в заданной системе координат.
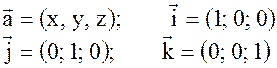
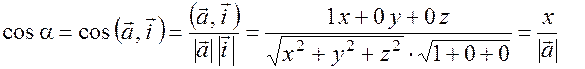
аналогично получим выражения для других углов.
Формулы для нахождения направляющих косинусов:
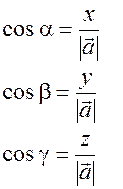 (8)
(8)
Тогда имеет место формула:
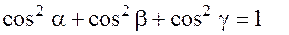 (9)
(9)
Доказать самостоятельно формулу (9).
Орт-вектор имеет координатами направляющие косинусы
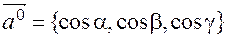 (10)
(10)
Пример 1:Найти 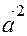 , если
, если 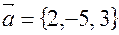 .
.
Решение: Вектор 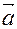 задан в ортонормированном базисе. Найдем
задан в ортонормированном базисе. Найдем 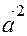 . Для этого воспользуемся формулой
. Для этого воспользуемся формулой 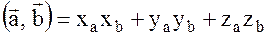 . Получим:
. Получим:
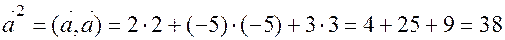 .
.
Пример 2: Вычислить 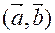 если
если 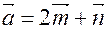 ,
, 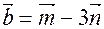 ,
, 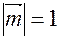 ,
, 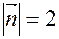 , угол между векторами
, угол между векторами 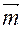 и
и 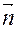 –
– 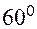 .
.
Решение: Векторы 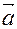 и
и 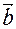 заданы в базисе векторов
заданы в базисе векторов 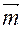 и
и 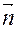 . Базис
. Базис 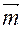 и
и 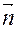 – не ортонормированный. Для решения воспользуемся определением скалярного произведения векторов и его свойствами.
– не ортонормированный. Для решения воспользуемся определением скалярного произведения векторов и его свойствами.
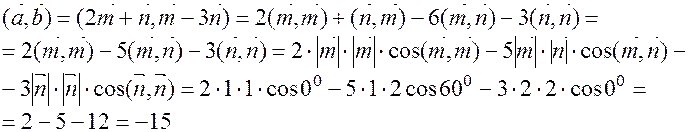
Векторное произведение векторов.
|
|
|
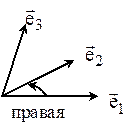 | 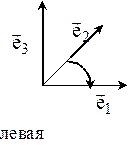 | 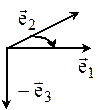 | |||
Определение: Упорядоченная тройка некомпланарных векторов
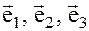 называется парвоориентированной (правой) если кратчайший поворот 1-го вектора ко 2-му из конца 3-го виден происходящим против часовой стрелки. В противном случае тройка векторов называется левой.
называется парвоориентированной (правой) если кратчайший поворот 1-го вектора ко 2-му из конца 3-го виден происходящим против часовой стрелки. В противном случае тройка векторов называется левой.
Определение: Векторным произведением векторов 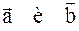 называется вектор
называется вектор 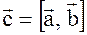 удовлетворяющей трём условиям:
удовлетворяющей трём условиям:
1. 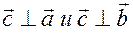
2. 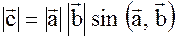
3. 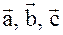 - образуют правую тройку.
- образуют правую тройку.
Модуль вектора  - численно равен площади параллелограмма построенного на векторах
- численно равен площади параллелограмма построенного на векторах 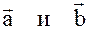 .
.
Свойства векторного произведения.
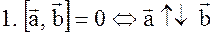 или
или 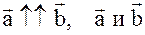 - коллинеарность
- коллинеарность
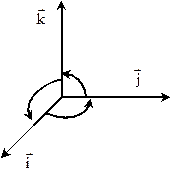
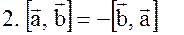 - антикоммутативность
- антикоммутативность
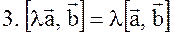
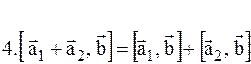
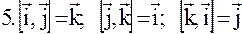
Механический смысл векторного произведения.
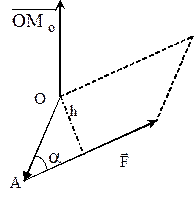 |
Пусть дано некоторое твёрдое тело, с неподвижной точкой О. В некоторой точке А этого тела приложена сила
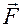 . Найти момент
. Найти момент 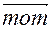 силы
силы 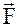 относительно точки О.
относительно точки О.
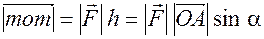 , где
, где 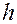 – плечо силы. Тогда из курса физики
– плечо силы. Тогда из курса физики 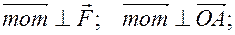 следовательно
следовательно 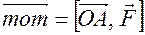 .
.
Дата добавления: 2020-12-12; просмотров: 291; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
