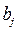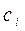Принятие решений в условиях неопределённости
Принятие решений в условиях неопределённости и риска
В некоторых задачах, приводящихся к игровым, имеется неопределённость, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос, процесс работы предприятий и торговых посредников и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности, т.е. между игроками отсутствует антагонизм. Такие игры называются играми с природой. Здесь первый игрок принимает решение, а второй действует случайно.
Для решения таких задач имеется рад критериев, которые используются при выборе оптимальной стратегии.
Задача. Оценить имеющиеся альтернативы, использую все известные критерии, предварительно отбросив доминируемые альтернативы, используя критерий Парето.
| Y1 | Y2 | Y3 | Y4 | Y5 | |
| 1 | 70 | 20 | 7 | 3 | -2 |
| 2 | 60 | 17 | 6 | 1 | -4 |
| 3 | 30 | 15 | 9 | 6 | 2 |
| 4 | 40 | 16 | 8 | 5 | 1 |
| 5 | 50 | 14 | 7 | 2 | -2 |
| 6 | 40 | 12 | 5 | 4 | 3 |
| p | 0,1 | 0,2 | 0,1 | 0,3 | 0,3 |
Решение:
1. Отбросим доминируемые альтернативы, используя критерий Парето:
| 1. | 70 | 20 | 7 | 3 | -2 | |
| ٧ | ٧ | ٧ | ٧ | ٧ | ||
| 2. | 60 | 17 | 6 | 1 | -4 | -доминируемая альтернатива |
| 1. | 70 | 20 | 7 | 3 | -2 | |
| ٧ | ٧ | ٨ | ٨ | ٨ | -несравнимые альтернативы | |
| 3. | 30 | 15 | 9 | 6 | 2 |
|
|
|
| 1. | 70 | 20 | 7 | 3 | -2 | |
| ٧ | ٧ | ٨ | ٨ | ٨ | -несравнимые альтернативы | |
| 4. | 40 | 16 | 8 | 5 | 1 |
| 1. | 70 | 20 | 7 | 3 | -2 | |
| ٧ | ٧ | || | ٧ | || | ||
| 5. | 50 | 14 | 7 | 2 | -2 | -доминируемая альтернатива |
| 1. | 70 | 20 | 7 | 3 | -2 | |
| ٧ | ٧ | ٧ | ٨ | ٨ | -несравнимые альтернативы | |
| 6. | 40 | 12 | 5 | 4 | 3 |
| 3. | 30 | 15 | 9 | 6 | 2 | |
| ٨ | ٨ | ٧ | ٧ | ٧ | -несравнимые альтернативы | |
| 4. | 40 | 16 | 8 | 5 | 1 |
| 3. | 30 | 15 | 9 | 6 | 2 | |
| ٨ | ٧ | ٧ | ٧ | ٨ | -несравнимые альтернативы | |
| 6. | 40 | 12 | 5 | 4 | 3 | |
| 4. | 40 | 16 | 8 | 5 | 1 | |
| || | ٧ | ٧ | ٧ | ٨ | -несравнимые альтернативы | |
| 6. | 40 | 12 | 5 | 4 | 3 |
Вывод: 2 и 5 альтернативы являются доминируемыми, поэтому их использовать не выгодно.
2. Критерий Вальда:
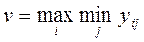
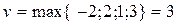- критерий крайнего пессимизма.
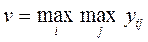
- критерий крайнего оптимизма.
Вывод: по критерию крайнего пессимизма оптимальной является 6 альтернатива, а по критерию крайнего оптимизма оптимальной является 1 альтернатива.
3. Критерий Гурвица:
α – коэффициент пессимизма. Пусть α=0,3, тогда имеем:
|
|
|
v1=0,3∙(-2)+(1-0,3)∙70=48,4;
v3=0,3∙2+(1-0,3)∙30=21,6;
v4=0,3∙1+(1-0,3)∙40=28,3;
v6=0,3∙3+(1-0,3)∙40=28,9;
v=max{48,4; 21,6; 28,3; 28,9}=48,4.
Вывод: по критерию Гурвица с заданным коэффициентом пессимизма α=0,3 оптимальной является 1 альтернатива.
4. Критерий Байеса-Лапласа:
v1=70∙0,1+20∙0,2+7∙0,1+3∙0,3-2∙0,3=12;
v3=30∙0,1+15∙0,2+9∙0,1+6∙0,3+2∙0,3=9,3;
v4=40∙0,1+16∙0,2+8∙0,1+5∙0,3+1∙0,3=9,8;
v6=40∙0,1+12∙0,2+5∙0,1+4∙0,3+3∙0,3=9;
v=max{12; 9,3; 9,8; 9}=12
Вывод: по критерию Байеса-Лапласа оптимальной является 1 альтернатива.
Теория игр
Часто приходится сталкиваться с ситуацией, в которой необходимо принимать решения в условиях неопределенности, когда два (или более) участника преследуют различные цели, а эффективность решения одного из них зависит от того, какие решения принял другой участник. Такие ситуации относятся к конфликтным. Для решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которая носит название теория игр.
Задачей теории игр является выработка рекомендаций для игроков, т.е. определение для них оптимальной стратегии. Стратегией игрока называется система правил, однозначно определяющих поведение игрока на каждом ходе в зависимости от ситуации, сложившейся в процессе игры. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.
|
|
|
К основным задачам теории игр относятся задачи конфликтных ситуаций, например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом и т.д.
Задача. Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.
| План продажи | Величина дохода, ден. ед. | ||
| К1 | К2 | К3 | |
| П1 | 8 | 4 | 2 |
| П2 | 2 | 8 | 4 |
| П3 | 1 | 2 | 8 |
Определить оптимальный план продажи товаров.
Решение:
Определим нижнюю и верхнюю цены игры:
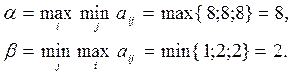
Так как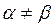 
, то седловая точка отсутствует и оптимальное решение следует искать в смешанных стратегиях игроков.
Обозначим: вероятность применения торговой фирмой стратегии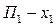 
, стратегии 
, 
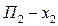; вероятность использования стратегии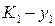 
, стратегии 
, 
.
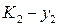Для первого игрока (торговой фирмы) математическая модель задачи имеет вид:
|
|
|
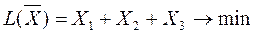
при ограничениях:
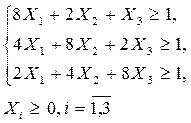
где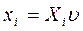 
Для второго игрока (конъюнктуры рынка и спроса покупателей) математическая модель задачи имеет вид:
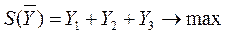
при ограничениях:
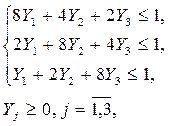
где 
Найдем оптимальное решение задачи для второго игрока симплексным методом. При этом последняя таблица имеет вид:
|
| БП | 1 | 1 | 1 | 0 | 0 | 0 |
|
| 
| 
| 
| 
| 
| |||
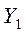
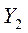
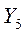
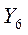
| 1 |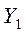
| 1 | 0 | 0 | 1/7 | -1/14 | 0 | 1/14 |
| 1 |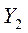
| 0 | 1 | 0 | -3/98 | 31/196 | -1/14 | 11/196 |
| 1 |
| 0 | 0 | 1 | -1/98 | -3/98 | 1/7 | 5/49 |
|
| 0 | 0 | 0 | 5/49 | 11/196 | 1/14 | 45/196 | |
Из таблицы следует, что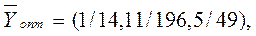 
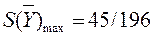. Цена игры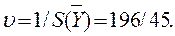 
Так как , то 
Оптимальная стратегия второго игрока:
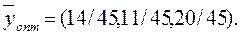
Стратегии первого игрока найдем из последней симплексной таблицы, используя метод соответствия переменных исходной и двойственной задач. Получим:
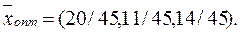
Ответ: Таким образом, торговая фирма на ярмарке должна придерживаться стратегии 
, при этом она получит доход не менее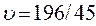 
ден. ед.
Планирование и прогнозирование
3.1. Сетевое планирование
Сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график, граф). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала её реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все работы в срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном применении как трудовых, так и финансовых ресурсов.
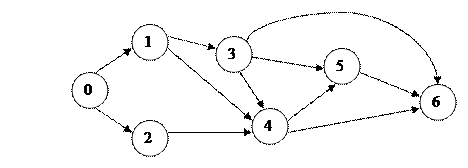
Задача. Дан сетевой граф. Найти критический путь с помощью линейной диаграммы и все временные параметры событий и работ.
4
3
4 6
8 2 3
5
7 2 9
Решение:
1. Строим линейную диаграмму.
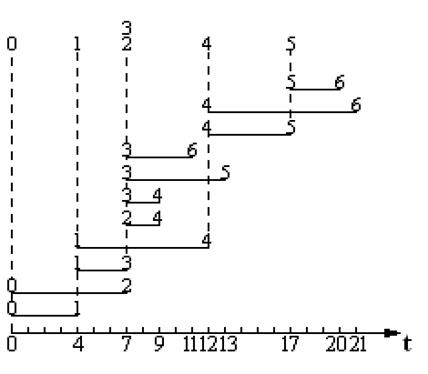
0→1→4→6 – критический путь
tкр = 21
2. Найдём все временные параметры событий.
tp – ранний срок свершения события;
t п – поздний срок свершения события;
R – резерв времени события.
| №события | tp | t п | R |
| 0 | 0 | 0 | 0 |
| 1 | 4 | 4 | 0 |
| 2 | 7 | 10 | 3 |
| 3 | 7 | 10 | 3 |
| 4 | 12 | 12 | 0 |
| 5 | 17 | 18 | 1 |
| 6 | 21 | 21 | 0 |
3. Найдем все временные параметры работ.
t ( i ; j ) – продолжительность работы;
t рн - ранний срок начала работы;
t ро - ранний срок окончания работы;
t по - поздний срок окончания работы;
t пн - поздний срок начала работы;
R - полный резерв времени работы;
R 1 - частный резерв времени работы первого вида;
R с - свободный резерв времени работы;
R н - независимый резерв времени работы.
| (i;j) | t(i;j) | t рн | t ро | t по | t пн | R | R1 | R с | R н |
| (0;1) | 4 | 0 | 4 | 4 | 0 | 0 | 0 | 0 | 0 |
| (0;2) | 7 | 0 | 7 | 10 | 3 | 3 | 3 | 0 | 0 |
| (1;3) | 3 | 4 | 7 | 10 | 7 | 3 | 3 | 0 | 0 |
| (1;4) | 8 | 4 | 12 | 12 | 4 | 0 | 0 | 0 | 0 |
| (2;4) | 2 | 7 | 9 | 12 | 10 | 3 | 0 | 3 | 0 |
| (3;4) | 2 | 7 | 9 | 12 | 10 | 3 | 0 | 3 | 0 |
| (3;5) | 6 | 7 | 13 | 18 | 12 | 5 | 2 | 4 | 1 |
| (3;6) | 4 | 7 | 11 | 21 | 17 | 10 | 7 | 10 | 7 |
| (4;5) | 5 | 12 | 17 | 18 | 13 | 1 | 1 | 0 | 0 |
| (4;6) | 9 | 12 | 21 | 21 | 12 | 0 | 0 | 0 | 0 |
| (5;6) | 3 | 17 | 20 | 21 | 18 | 1 | 0 | 1 | 0 |
Ответ: 0→1→4→6 – критический путь, т.е. наиболее продолжительный полный путь в сетевом графе; tкр = 21 – минимальное время выполнения всех работ.
Прогнозирование
Прогноз есть некоторое знание о возможном будущем.
Прогнозирование является одним из основных этапов управленческого процесса. Прогнозирование позволяет предвидеть возможные последствия принимаемых решений, а так же тенденции развития проблемных ситуаций. Прогнозирование в процессе разработки, принятия и реализации решений выполняется многократно.
Задача. Построить прогнозную функцию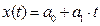 
полиномиальным методом и методом наименьших квадратов. Сделать прогноз на 2003 год.
| x | 20,2 | 26,6 | 22 | 25,9 | 21,6 |
| t | 1998 | 1999 | 2000 | 2001 | 2002 |
Решение:
1. Полиномиальный метод.
Так как вид прогнозной функции линейный, то достаточно взять два последних результата наблюдений. Составим систему уравнений:
Решая эту систему уравнений, получаем: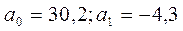 
.
Таким образом, прогнозная функция имеет следующий вид:
x ( t )=30,2-4,3∙ t
x(2003)=30,2-4,3∙3=17,3 – прогноз на 2003 год.
2. Метод наименьших квадратов.
Для удобства вычислений составим вспомогательную таблицу:
| t | x | t² | x∙t | |
| 1 | 20,2 | 1 | 20,2 | |
| 2 | 26,6 | 4 | 53,2 | |
| 3 | 22 | 9 | 66 | |
| 4 | 25,9 | 16 | 103,6 | |
| 5 | 21,6 | 25 | 108 | |
| ∑ | 15 | 116,3 | 55 | 351 |
Составим систему уравнений:
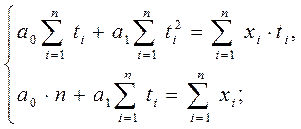
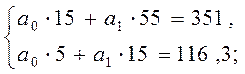
Решая эту систему уравнений, получаем: 
Таким образом, прогнозная функция имеет следующий вид:
x ( t )=22,63+0,21∙ t
x(2003)=22,63+0,21∙6=23,89 – прогноз на 2003 год.
Ответ: 1.полиномиальный метод: x ( t )=30,2-4,3∙ t ; x(2003)=17,3;
2. метод наименьших квадратов: x ( t )=22,63+0,21∙ t ; x(2003)=23,89.
Приложение
Дата добавления: 2021-01-21; просмотров: 265; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!