Закон распределения Пуассона.
Лекция№7
Законы распределения дискретных случайных величин
Вопросы:
Биномиальное распределение .
Геометрическое распределение.
Распределение Пуассона.
Гипергеометрическое распределение.
Биномиальное распределение
Дискретная случайная величина Х с конечным числом возможных значений xk=k=0,1,2,…,n называется распределенной по биномиальному закону, если соответствующие вероятности даются формулой Бернулли
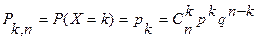 . (1)
. (1)
Найдем математическое ожидание дискретной случайной величины Х, имеющей биноминальное распределение.
Случайная величина Х - «число появления события А в n независимых испытаниях» можно представить в виде суммы 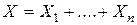 , где
, где 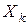 - число появления события A в k-ом испытании (k=0,1,…,n). На основании свойства математического ожидания имеем:
- число появления события A в k-ом испытании (k=0,1,…,n). На основании свойства математического ожидания имеем: 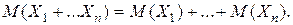
Случайная величина 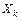 - число появлений события А в одном испытании – может принимать только два значения:
- число появлений события А в одном испытании – может принимать только два значения:  (событие А наступило) с вероятностью р и
(событие А наступило) с вероятностью р и 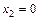 (А не наступило) с вероятностью
(А не наступило) с вероятностью 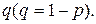
Следовательно, 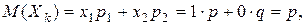
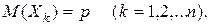
Следовательно, 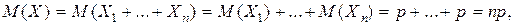 М(Х)=np.
М(Х)=np.
Таким образом, математическое ожидание дискретной случайной величины, распределенной по биноминальному закону с параметрами n и p, равно произведению параметров.
Второй способ:
По биномиальному закону распределено, например, число успехов в n испытаниях Бернулли. Воспользуемся биномом Ньютона 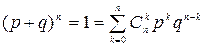 (2)
(2)
|
|
|
Из (2) видно, что формула (1)- это k-й член разложения бинома Ньютона. Отсюда и название распределения. Из этой же формулы (2) видно, что 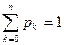 .
.
Найдем математическое ожидание.

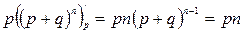 .
.
(Индекс внизу означает, что производная берется по p.)
Итак, 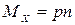 . (3)
. (3)
Для вычисления дисперсии воспользуемся формулой 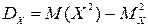 (4)
(4)
Продифференцируем (2) по p два раза и умножим полученное равенство на p2. В результате получим
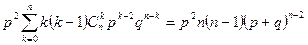 ,
,
или 
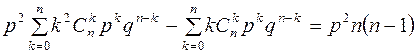 ,
,
или 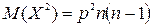 . (5)
. (5)
Подставляя 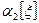 из (5) в (4), найдем с учетом (3)
из (5) в (4), найдем с учетом (3) 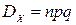 (6)
(6)
Можно доказать, что мода М0 случайной величины ξ, распределенной по биномиальному закону, удовлетворяет условию
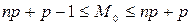 . (7)
. (7)
В частности, если 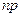 число натуральное, то оно и является модой. Коэффициент асимметрии определяется формулой
число натуральное, то оно и является модой. Коэффициент асимметрии определяется формулой 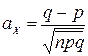 . (8)
. (8)
Геометрическое распределение
Дискретная случайная величина Х, возможными значениями которой является бесконечная последовательность натуральных чисел 1,2,3,…, а соответствующие вероятности даются формулой
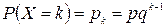 , (9)
, (9)
|
|
|
называется распределенной по геометрическому закону. Если число испытаний Бернулли не ограничивать, а проводить их до первого успеха, то число всех испытаний (вплоть до первого успеха) есть случайная величина ξ, распределенная по геометрическому закону. Название закона обязано тому, что вероятности (9) образуют геометрическую прогрессию со знаменателем q.
Проверим условие 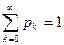 . Действительно, запишем ряд, членами которого являются вероятности
. Действительно, запишем ряд, членами которого являются вероятности
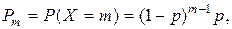 или
или 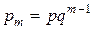
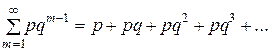
Этот ряд является геометрическим рядом с первым членом p и знаменателем q. Поскольку 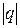 <1 (0<p<1, 1-p=q, 0<q<1), то геометрический ряд сходится и его сумма
<1 (0<p<1, 1-p=q, 0<q<1), то геометрический ряд сходится и его сумма 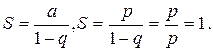
Итак,  т.е. выполнено равенство.
т.е. выполнено равенство. 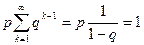 . (10)
. (10)
Найдем математическое ожидание. В соответствии с формулой получаем, 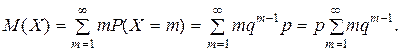
Поскольку члены ряда 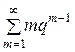 являются производными соответствующих членов
являются производными соответствующих членов
ряда 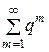 и
и 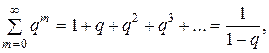
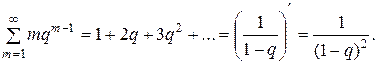
Следовательно,
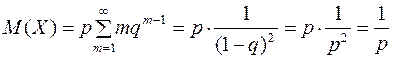
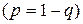 ,
, 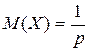 (p>0).
(p>0).
Для вычисления дисперсии воспользуемся формулой для вычисления дисперсии и формулами для сумм рядов:
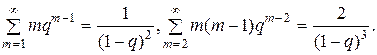
Найдём сначала математическое ожидание квадрата величины X:
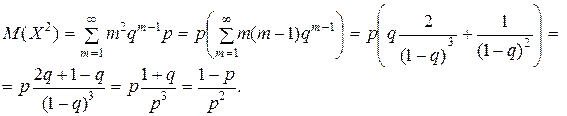
Таким образом, 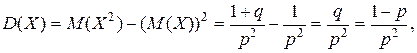 (13)
(13)
Закон распределения Пуассона.
СВ  принимает бесконечно счетное число значений с вероятностью, определяемой по формуле Пуассона
принимает бесконечно счетное число значений с вероятностью, определяемой по формуле Пуассона 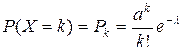 ,
, 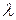 - параметр распределения.
- параметр распределения.
|
|
|
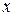
| 0 | 1 | … | 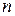
|

| 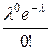
| 
| … | 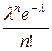
|
Замечание. При  и
и 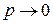 биноминальный закон стремиться к закону Пуассона.
биноминальный закон стремиться к закону Пуассона.
Числовые характеристики:
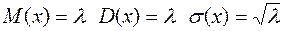
Дата добавления: 2021-01-21; просмотров: 52; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
