ОПРЕДЕЛЕНИЕ НАВИГАЦИОННЫХ ПАРАМЕТРОВ

ЛЕКЦИЯ 6. КООРДИНАТНЫЕ ТРЕХГРАННИКИ

Согласно ГОСТ 20058-80

Нормальная система координат О X_gY_gZ_g

Начало О расположено в центре масс летательного аппарата. Ось О Y_g направлена вверх по местной вертикали, а направление осей О X_g и О Z_g выбирается в соответствии с задачей.

Связанная система координат О X Y Z

Продольная ось ОХ расположена в плоскости симметрии летательного аппарата и направлена от хвостовой к носовой части летательного аппарата. Нормальная ось О Y расположена в плоскости симметрии летательного аппарата и направлена к верхней части летательного аппарата. Поперечная ось О Z перпендикулярна плоскости симметрии и направлена к правой части летательного аппарата.

Скоростная система координат О X _а Y _а Z _а

Начало О расположено в центре масс летательного и аппарата. Ось О X_а совпадает с вектором воздушной скорости летательного аппарата. Ось подъёмной силы О Y_а расположена в плоскости симметрии, направлена к верхней части летательного аппарата. Боковая ось О Z_а дополняет скоростную ось О X_а и ось подъёмной силы О Y_а до правой системы координат.

Углы между связанной и нормальной системами координат

Угол рыскания y - угол между осью OX_g нормальной системы координат и проекцией продольной оси OX на горизонтальную плоскость О X_gZ_g нормальной системы координат; угол положителен, если ось OX_g совмещается с проекцией продольной оси на горизонтальную плоскость поворотом вокруг оси OY_g по часовой стрелке, если смотреть из начала координат в положительном направлении оси OY_g.

Угол тангажа J - угол между продольной осью ОХ и горизонтальной плоскостью О X_gZ_g нормальной системы координат. Угол тангажа положителен, когда продольная ось находится выше горизонтальной плоскости О X_gZ_g.

Угол крена g - угол между поперечной осью О Z и осью О Z_g нормальной системы координат, смещенный в положение, при котором угол рыскания равен нулю. Угол крена положителен, если смещенная ось О Z_g совмещается с поперечной осью О Z поворотом вокруг продольной оси по часовой стрелке, если смотреть в направлении этой оси.

Переход от связанной системы координат к нормальной системе координат осуществляется тремя последовательными поворотами на угол крена, угол тангажа и угол рыскания.

Углы, определяющие направление скорости летательного аппарата в связанной системе координат

Угол атаки a - угол между продольной осью OX и проекцией скорости летательного аппарата на плоскость О XY связанной системы координат. Угол положителен, если проекция скорости на нормальную ось OY отрицательна.

Угол скольжения β - угол между направлением скорости летательного аппарата и плоскостью О XY связанной системы координат. Угол скольжения положителен, если проекция скорости на поперечную ось положительна.

Рисунок 6.1

Соотношение между углами и угловыми скоростями в связанной системе координат имеют вид.

Отобразим повороты по J и g на плоскости.

Рисунок 6.2

Из рисунков следует:

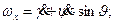
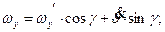
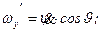
Отсюда:

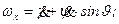
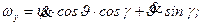(6.1)

Умножим второе уравнение (6.1) на sin g, а третье на cos g и сложим.

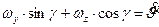Умножим второе уравнение (6.1) на cos g, а третье на sin g и вычтем.

Отсюда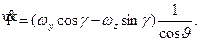

Подставим в первое уравнение (6.1) выражение для 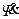, получим

Итак, имеем уравнения

(6.2)

В Международном стандарте (JSO) оси координат направлены иначе. Основное отличие в том, что ось OZ направлена вниз, а ось OY направлена вправо. При этом положительное направление угла рыскания – по часовой стрелки; Положительные направления тангажа (q) и крена (f) совпадают с тангажом (u) и креном (g) по ГОСТ 20058-80.

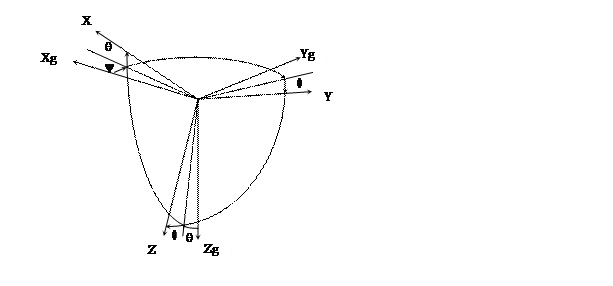
Рисунок 7.3

В авиационной навигации используется ещё некоторые углы, не охваченные ГОСТ 20058-80.

Вместо угла рыскания используется гироскопический курс. Положительное направление гироскопического курса противоположно положительному направлению углу рыскания и направлено по часовой стрелке. С учётом этого для гироскопического курса формулы (7.2) будут иметь вид.

(6.3)

Системы измерения курса

Курсом летательного аппарата называется угол между вертикальной плоскостью принятой за начало отсчёта и проекцией продольной оси летательного аппарата на плоскость горизонта. Угол отсчитывается по часовой стрелке в пределах от нуля до 360°. Положительное направление вправо от начала отсчёта, если смотреть сверху. В зависимости от начала отсчёта различают курсы истинный, магнитный, приведенный

- истинный курс y_и – угол, отсчитанный от плоскости истинного (географического) меридиана;

- магнитный курс y_м – угол, отсчитанный от плоскости магнитного меридиана;

- приведенный курс y_пр – угол, отсчитанный от плоскости истинного (географического) меридиана в точке старта.

Истинный и магнитный курсы связаны соотношением

y_и = y_м+ DМ , где DМ – магнитное склонение.

В инерциальной навигации используются следующие системы координат.

Разновидности нормальной системы координат.

Географическая система координат OENH (нормальная)

Начало О расположено в центре масс инерциальной системы. Ось OE направлена на Восток, ось ON – на Север, ось OН – по географической вертикали вверх.

Геоцентрическая система координат OE ¢ N ¢ H ¢(нормальная)

Начало О расположено в центре масс инерциальной системы. Ось OE¢ направлена на Восток, ось ON¢ – на Север, ось OН¢– по геоцентрической вертикали вверх.

Гравитационная система координат OE ² N ² H ²(нормальная)

Начало О расположено в центре масс инерциальной системы. Ось OE² направлена на Восток, ось ON² – на Север, ось OН²– по гравитационной вертикали вверх.

Опорная система координат О x h z

Система координат О x h z лежит в плоскости географического горизонта и развернута относительно OENH на угол c. Угол c измеряют по часовой стрелки обычно от оси ON к оси O h, но так как гироскопический курс определяется относительно оси O x вправо по часовой стрелке, то удобно угол c измерять до оси O x. В этом случае
y_и = c + y_г.

Следует учитывать, что положительное направление угла c и y_г противоположно положительному направлению угла рыскания y.

Опорная система координат O x ¢ h ¢ z ¢

Система координат O x¢h¢z¢ отличается от O x h z тем, что ось O z¢ направлена по геоцентрической вертикали вверх и угол c измеряется от оси ON ¢ системы координат OE ¢ N ¢ H ¢

Опорная система координат O x ² h ² z ²

Система координат O x ² h ² z ² отличается от O x h z тем, что ось O z ² направлена по гравитационной вертикали вверх и угол c измеряется от оси ON ² системы координат OE ² N ² H ².

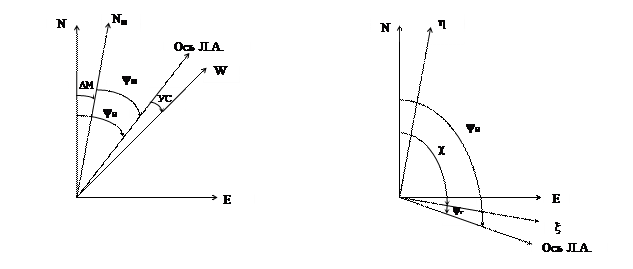Рисунок 6.4

. Геоцентрическая земная система координат ОXYZ (в соответствии с ГОСТом Р 51794-2001 г.)

Начало системы координат расположено в центре масс Земли, ось OZ направлена по оси вращения Земли в сторону Северного полюса, оси OX и OY лежат в плоскости экватора; ось OX проходит через точку пересечения Гринвичского меридиана с экватором (Рисунок 7.5).

Система углов

Курсовой угол - угол, отсчитанный по часовой стрелке от горизонтальной проекции продольной оси летательного аппарата до горизонтальной проекции линии, соединяющей летательный аппарат с объектом. От курсового угла радиостанции (КУР), который измеряют с помощью бортового радиокомпаса (АРК), берёт начало общее название курсового угла как КУР.

Путевой угол (ПУ) - угол, который образует горизонтальная составляющая вектора скорости с касательной к северному направлению меридиана. Он считается положительным при повороте V в направлении от севера к востоку.

Угол сноса (УС) – угол между вектором воздушной и путевой скорости. Путевой угол и угол сноса связаны соотношением УС = ПУ- y_и.

Направление ветра – это угол между северным направлением меридиана и направлением горизонтального перемещения воздушных масс. Угол отсчитывается по часовой стрелке в пределах от нуля до 360°. Направление ветра, принятое в метеорологии (откуда дует), отличается от аэронавигационного направления (куда дует) на 180°.

Азимут (А) – угол, отсчитанный по часовой стрелке от северного направления меридиана до горизонтальной проекции линии, соединяющей точку наблюдения с объектом. Слово азимут происходит от арабского слова Ас-самт (направление). Азимут может быть относительно магнитного меридиана (Ам). Если не указано специально, то подразумевают Азимут относительно истинного меридиана.

Пеленг (П) – это угол, отсчитанный по часовой стрелке от северного направления меридиана до горизонтальной проекции линии, соединяющей летательный аппарат с объектом, на который пеленг определяют. Пеленг может быть относительно магнитного меридиана (Пм). Если не указано специально, то подразумевают пеленг относительно истинного меридиана. КУР связан с пеленгом соотношением
П = КУР + y_и или Пм = КУР + y_м
слово пеленг происходит от голл. Peiling. В авиационной навигации определение пеленга совпадает с определением азимута. В геодезии пеленгом называется угол между направлением, принятым за начало отсчёта и направлением на объект. То есть пеленг – это более общее понятие, чем азимут. В некоторых случаях под пеленгом понимают курсовой угол. На английский язык пеленг и азимут переводятся как bearing.

Существует понятие обратный пеленг и обратный азимут – это угол от объекта на точку наблюдения. Часто смешивают эти понятия, так как относительно радиостанции измеренный азимут (пеленг) является прямым, а для самолёта он является обратным. Поэтому, какой угол является прямым, а какой обратным зависит от принятой точки отсчёта.

Для однозначности в некоторых документах угол от радиостанции на самолёт называют азимутом, а угол от самолёта на радиостанцию - пеленгом.

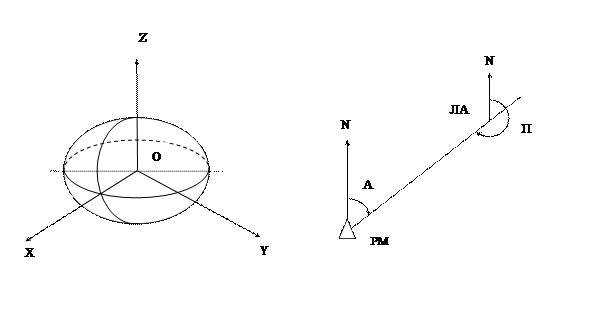
Рисунок 6.5

ОПРЕДЕЛЕНИЕ НАВИГАЦИОННЫХ ПАРАМЕТРОВ

Введем следующие системы координат

ОXYZ – геоцентрическая система координат, связанная с Землей (в соответствии с ГОСТ Р 51794-2001 г.);

OENH - географический трехгранник;

О x h z – опорный трехгранник, лежащий в плоскости географического горизонта и развернутый относительно OENH на угол c.

Относительные скорости в географической системе координат определяются соотношениями

Если опорный трёхгранник вращается относительно географического со скоростью 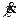, то при проектировании этих скоростей на оси опорного трёхгранника, имеем:

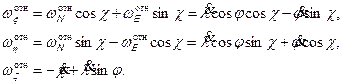(6.4)

После соответствующих преобразований получим

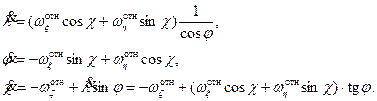(6.5)

Из-за присутствия деления на эти формулы в бортовых комплексах не применяются.

В некоторых системах расчёты производятся в ортодромической системе координат. Самый простой способ направить ортодромию из точки старта на географический север (но это не обязательно). Очевидно, что в этом случае вероятность попадания на полюса ортодромии, где долгота не определяется, очень мала. Рассмотрим трёхгранники

Oxhz – опорный, Ox^ортh^ортz^орт– трёхгранник, материализующий ортодромическую систему координат, ONE - трёхгранник, материализующий географическую систему координат.

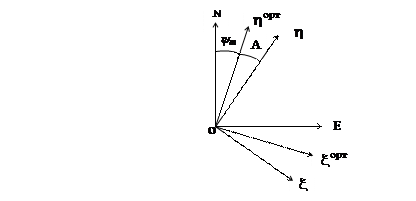
Рисунок 6.6

Где y _m – угол сходимости меридианов,

А – угол ориентации платформы.

Дифференциальные уравнения для ортодромических координат представляются аналогично географическим координатам в виде

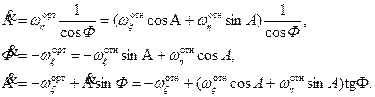(6.6)

Преобразование из географических координат в ортодромические и из ортодромических в географические производится по формулам, изложенным в разделе 5.

Рассмотрим более точный метод. Метод направляющих косинусов.

Понимание сути направляющих косинусов. можно получить из следующих соображений.

Предположим, что имеются две различные системы прямоугольных координат с общим началом: OX₁Y₁Z₁ и OX₂Y₂X₂. Произвольный вектор может быть выражен в виде составляющих как в системе OX₁Y₁Z₁, так и в системе OX₂Y₂X₂.

= x ₁ ∙ i ₁ + y ₁ ∙ j ₁ + z ₁ ∙ k ₁ = x ₂ ∙ i ₂ + y ₂ ∙ j ₂ + z ₂ ∙ k ₂ .

Где i ₁, j ₁, k ₁, i ₂, j ₂, k ₂– единичные орты соответственно системы OX₁Y₁Z₁ и OX₂Y₂X₂.

Предварительно напомним, что скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла между ними. Умножим скалярно справа левые и правые части исходного уравнения, сначала на орт i ₂, затем на орт j ₂, затем на орт k ₂. Соответственно получим три уравнения:

x₂ = x₁∙(i₁ i₂)+y₁∙(j₁ i₂) +z₁∙(k₁ i₂),

y₂ = x₁∙(i₁ j₂)+y₁∙(j₁ j₂) +z₁∙(k₁ j₂),

z₂ = x₁∙(i₁ k₂)+y₁∙(j₁ k₂) +z₁∙(k₁ k₂).

Здесь было учтено, что

(i₂ i₂)=(j₂ j₂)= (k₂ k₂)=1, а (j₂ i₂)=(i₂ j₂)= (j₂ k₂) = (k₂ j₂)= (i₂ k₂) = (k₂ i₂)=0.

С учетом свойств скалярного произведения в матричном виде уравнения запишем в виде:

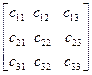= ∙ = . (6.7)

где: 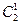– матрица направляющих косинусов углов между осями первого и второго координатных трехгранников;

Аналогично умножая скалярно левые и правые части исходного уравнения сначала на орт i ₁, затем на орт j ₁, а затем на орт k ₁ получим:

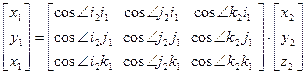Так как , то можно записать

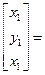
∙ = (6.8)

Таким образом, с помощью соответствующей матрицы направляющих косинусов легко осуществляется перепроектирование любого вектора из одного координатного трехгранника в другой.

При подстановке (6.8) в (6.7) получим:

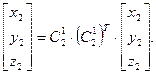
Отсюда следует, что произведение равно единичной матрице E, у которой диагональные элементы равны 1, а все остальные равны 0.

Аналогично при подстановке (6.7) в (6.8) получим то, что произведение 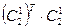также равно единичной матрице E. Приравнивая элементы произведения упомянутых матриц к элементам единичной матрицы, получим следующие свойства:

- Сумма квадратов элементов любой строки (столбца) равна единице

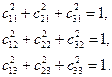(6.9)

- скалярное произведение любых двух строк (столбцов) равно нулю,

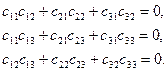
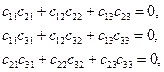(6.10)

По определению, если для матрицы справедливо 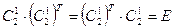, то такая матрица является ортогональной. Для ортогональной матрицы справедливо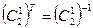

Из свойств (6.9) и (6.10) выводятся важные соотношения. Из первых двух строк (6.10) запишем:

, ,

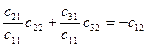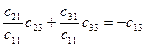Решив эти уравнения получим:

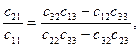
Эти равенства можно переписать в виде пропорций:

(6.11)

Где через s обозначим общую для всех пропорций величину. Пропорции обладают следующим свойством:

Если 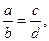то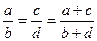

Применим это свойство для квадратов членов пропорции:

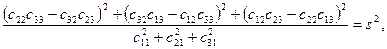
С учётом (6.9):

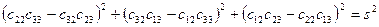
Воспользуемся тождеством Эйлера

Применив его к нашему уравнению и с учётом (6.9) и (6.10) получим:

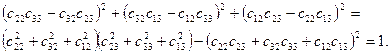
Следовательно s² = 1 и значит s = ±1. Чтобы решить какой знак взять, предположим, что начальный и конечный трёхгранники совпадают. В этом случае , остальные элементы будут нулевыми. Из первого элемента соотношения (6.11) следует s = 1, а из формул (6.11) имеем:

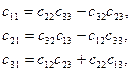
Аналогично, используя другие пары уравнений (5.4), получим:

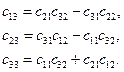(6.12)

Таким образом любая строка (столбец) может быть получена как векторное произведение предыдущих двух строк (столбцов). Из девяти косинусов независимыми являются только шесть.

Для матриц направляющих косинусов как матриц линейных преобразований справедливы следующие формулы:

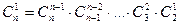; (6.13)

Здесь: – матрица направляющих косинусов углов между осями i-го и j-го координатных трехгранников;

Т – символ транспонирования матрицы.

Матрицы направляющих косинусов углов между осями координатных трехгранников являются одновременно матрицами линейных преобразований базисов этих координатных трехгранников, поэтому они называются матрицами поворотов от одного трехгранника к другому.

Получим выражение для таблицы (матрицы) направляющих косинусов углов между осями географического и гринвичского трехгранников. На рис. 6.7 изображены эти трехгранники, причем для удобства и наглядности дальнейших выкладок их вершины совмещены.

Примечание. Так как поступательное перемещение твердого тела (в том числе – координатного трехгранника) не меняет его угловую ориентацию, то при составлении выражений для параметров взаимной угловой ориентации координатных трехгранников их вершины часто совмещаются в одной точке, чем достигается наибольшая наглядность.

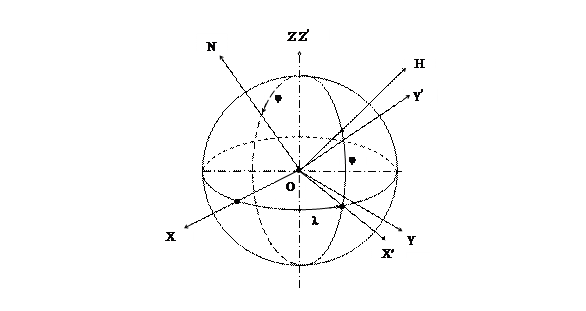
Рисунок 6.7

Связь между трехгранниками О XYZ и О x h z определяется следующим образом

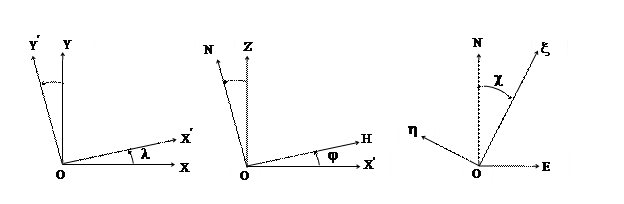
Рисунок 6.8

в матричной форме ;

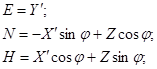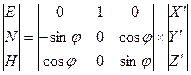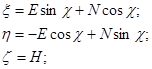в матричной форме .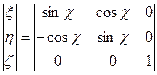

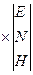Обозначим приведенные матрицы поворотов соответственно через L, Ф, А. Матрица преобразования будет иметь вид

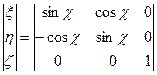
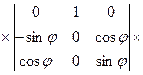
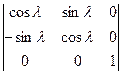
или

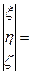
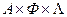
Обозначим матрицу преобразований через С, тогда

. (6.14)

Зададимся целью получить

Сделаем предварительные преобразования. При этом учтем, что матрицы А, Ф, L являются ортогональными с определителем, равным 1. Для них справедливо 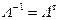и 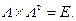Аналогично 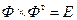и

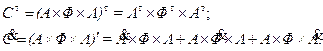
Отсюда

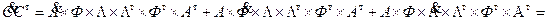
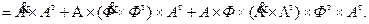
Проведем предварительные вычисления

;

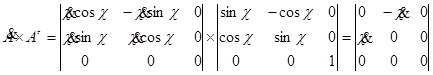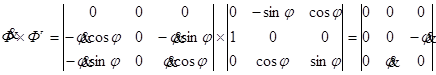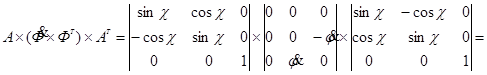
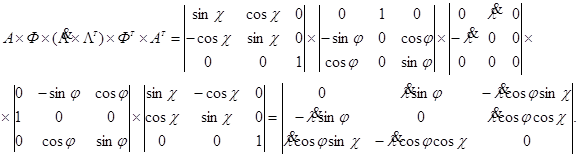
С учетом всех составляющих будем иметь

Замечаем, что элементы этой матрицы являются проекциями угловой скорости на оси x, h, z. В соответствии с (6.4)

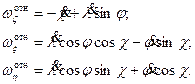
Тогда можно представить

Умножим обе части равенства справа на U, получим уравнение Пуассона

Отсюда имеем линейные дифференциальные уравнения.

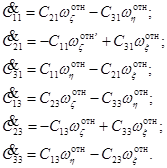
Задав начальные условия можно решить указанную систему уравнений. Еще один элемент матрицы определяем по формуле (6.12).

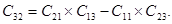
После вычисления элементов матрицы направляющих косинусов определяем основные навигационные параметры

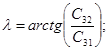(6.15)

курс: y_и = c + y_г.

Если задать угол c до оси h, то и y_и = c + y_г. + 90°;

При позиционной коррекции корректным будет исправление элементов матрицы С. При наличии невязок Dj, Dl, Dc корректирующие значения элементов матрицы Сопределяются варьированием этой матрицы.

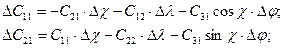
Дополнительные элементы получаются по формулам

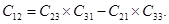
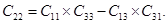
Если в качестве исходной системы координат использовать систему, представленную на Рисунке 6.9, где ось ОХ расположена вдоль полярной оси, ось Z лежит в плоскости нулевого меридиана, то матрица направляющих косинусов имеет следующий вид

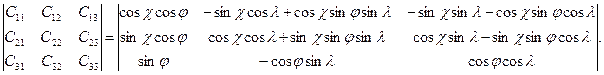
(6.16)

Рисунок 6.9

Линейные дифференциальные уравнения имеют вид

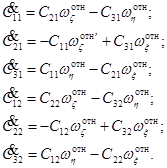(6.17)

Дополнительный элемент матрицы определяется по формуле

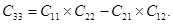
Основные навигационные параметры определяются по формулам

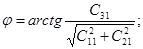
y_и = c + y_г. (6.18)

В некоторых системах, например LTN-51, все повороты (в том числе на угол 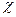) осуществляются в правильном направлении, то есть против часовой стрелки, если смотреть с вершины оси вокруг которой осуществляется поворот. В этом случае в исходной матрице изменяется на - и конечные уравнения принимают вид

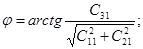
y_и = - c + y_г. (6.19)

Дата добавления: 2021-01-21; просмотров: 990; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!