Достаточное условие экстремума.
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Конспект лекции №3
по теме:
«Монотонность функции»
 |
Волгодонск
2011
Признаки монотонности функции.
Пусть функция 
определена и непрерывна на промежутке (a;b).
Определение: Функция называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется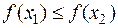 
( 
).
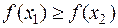Определение: Функция называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 
( 
).
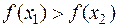Теорема 1 .
Для того чтобы функция , дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е.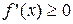 
, и достаточно, чтобы 
.
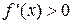Доказательство:
Необходимость.
Пусть f(x) возрастает на (a;b). Тогда для любых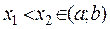 
выполняется .
Þ 
Þ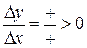 
.
По определению производной: 
.
Достаточность.
Пусть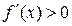 
на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
Тогда на (х1; х2) выполняется условие теоремы Лагранжа:
существует точка с Î(х1; х2) такая, что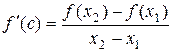 
.
Þ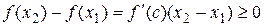 
(т.к. ).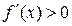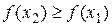
|
|
|
Þ 
. Þ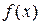 
возрастает на (a;b).
Ч.т.д.
Теорема 2 .
Для того чтобы функция , дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке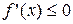 
и достаточно, чтобы 
.
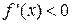Доказательство проводится аналогично.
Пример: Найти интервалы возрастания и убывания функции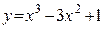 
.
.
.
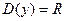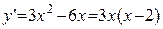Þ 
.
Экстремум функции.
Пусть функция определена в окрестности точки x0.
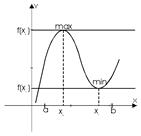
Определение: Точка x0 называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство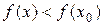 
.
x0 — max.
Определение: Точка x0 называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство 
.
x0 — min.
Точки локального максимума и минимума называются точками экстремума.
Необходимое условие экстремума дифференцируемой функции.
Если функция , дифференцируемая в точке x0, имеет в этой точке экстремум, то производная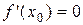 
.
Доказательство:
Пусть для определенности точка x0 — max.
Тогда по определению существует такая ее окрестность 
, в которой выполняется неравенство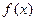 
< 
.
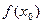Т.о. на интервале в точке x0 функция принимает наибольшее значение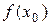 
.
Тогда по теореме Ферма: .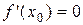
|
|
|
Аналогично доказывается для минимума функции.
Ч.т.д.
Однако, возможна ситуация, когда функция будет иметь экстремум в точке x0 в том случае, когда производная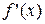 
не существует.
Точки, в которых производная 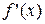либо равна 0, либо не существует, называются критическими точками производной.
Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.
Замечание 2. Функция имеет экстремум только в критических точках.
Достаточное условие экстремума.
Пусть функция определена в критической точке x0 и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x0. Если «при переходе» через точку x0 слева направо производная меняет знак с плюса на минус, то x0 – точка максимума; с минуса на плюс – точка минимума.
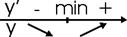
Доказательство:
Пусть производная меняет знак с «+» на «-».
Тогда слева от х0, т.е. на (х0-δ,х0) 
.
Þ слева от х0 функция 
возрастает.
Справа от х0, т.е. на (х0, х0+δ)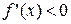 
.
Þ справа от х0 функция убывает.
Т.о. в окрестности точки х0 выполняется
неравенство 
.
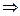х0 – точка локального максимума.
Аналогично доказывается для минимума.
|
|
|
Ч.т.д.
Пример: Исследовать функцию на монотонность и найти точки экстремума.
а)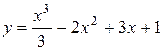 
.
1. Область определения функции D(y)=R.
2. 
.
Критические точки: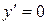 
. 
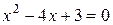Þ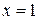 
, 
.
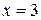| x | (-∞;1) | x=1 | (1;3) | x=3 | (3;+∞) |
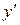
| + | 0 | – | 0 | + |
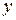
| возрастает | max
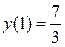
| убывает | min y(3)=1 | возрастает |
б)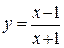 
.
1. Область определения функции D(y): x¹-1.
2. 
;
.
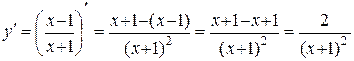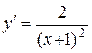Критические точки: 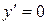, т.е. числитель равен нулю Þ нет точек;
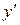– не существует, т.е. знаменатель равен нулю Þ 
.
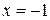| x | (-∞;-1) | x=-1 | (-1;+∞) |
|
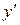
| + | не существует | + |
|
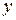
| возрастает | не существует | возрастает |
Точек экстремума нет.
Вопросы для самоконтроля.
1. Какая функция называется невозрастающей?
2. Какая функция называется убывающей?
3. Сформулировать признак монотонности.
4. Что такое критические точки?
5. Какая точка называется точкой максимума?
6. Какая точка называется точкой минимума?
7. Сформулировать необходимое условие экстремума.
8. Сформулировать достаточное условие экстремума.
Задачи для самоконтроля.
Исследовать функцию на монотонность и найти точки экстремума:
|
|
|
а) 
, б) 
.
Решение типовых задач.
Исследовать функцию на монотонность и найти точки экстремума:
а)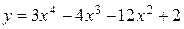 
.
1. Область определения функции D(y)=R.
2. 
.
Критические точки: .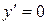 
, 
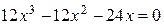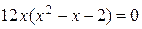Þ 
, 
, 
.
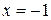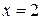| x | (-∞;-1) | x=-1 | (-1;0) | x=0 | (0;2) | x=2 | (3;+∞) |
|
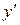
| – | 0 | + | 0 | – | 0 | + |
|
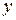
| убывает | min y(-1)=-3 | возрастает | max y(0)=2 | убывает | min y(2)=-30 | возрастает |
б)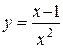 
.
1. Область определения функции D(y): x¹0.
2. 
;
.
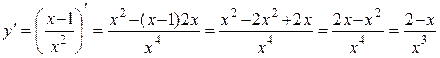Критические точки: 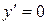, т.е. числитель равен нулю Þ ;
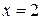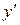– не существует, т.е. знаменатель равен нулю Þ .
| x | (-∞;0) | x=0 | (0;2) | x=2 | (2;+∞) |
|
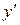
| – | не существует | + | 0 | − |
|
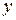
| убывает | не существует | возрастает | max y(2)=0,25 | убывает |
Дата добавления: 2021-01-21; просмотров: 67; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!