Измерение индукции магнитного поля с помощью

Лабораторная работа № 5

Цель работы: Ознакомиться с одним из широко используемых на практике методов измерения и исследования магнитных полей с помощью миллитесламетра портативного универсального ТПУ с датчиком Холла; исследовать магнитное поле внутри длинного соленоида

Приборы и принадлежности: соленоид, миллитесламетр портативный универсальный ТПУ с датчиком Холла; блок питания для соленоида.

Краткое теоретическое введение

Методы создания магнитного поля

При исследовании некоторых свойств вещества, при изучении движения заряженных частиц по необходимым траекториям часто возникает необходимость в создании магнитных полей различных конфигураций.

Простейшим устройством, создающим магнитное поле, является проводник с током (рис. 1 а). В пространстве вокруг него существует неоднородное поле.

Для того, чтобы иметь представление о распределении магнитных полей в пространстве, удобно использовать графический способ представления полей - при помощи силовых линий магнитной индукции.

Линии магнитной индукции - это такие линии, касательные к которым в каждой точкеполя совпадают с направлением вектора магнитной индукции 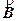в этой точке (рис. 1, точки A, C, D). На рис. 1 представлены различные конфигурации проводников с током и расположение линий магнитной индукции вокруг них. Здесь видны особенности линий магнитной индукции, которые отражают важные свойства магнитных полей.

Линии магнитной индукции всегда замкнуты: они не имеют ни начала, ни конца. Это говорит о том, что магнитное поле – вихревое поле.

Для определения направления вектора магнитной индукции поля, созданного вокруг проводника с током используют либо правило буравчика (штопора) , либо правило правой руки.

Согласно правилу буравчика, если ток течет по прямому проводнику ( прямой ток), то в этом направлении должен перемещаться буравчик. Тогда направление вращения ручки буравчика покажет направление силовых линий магнитного поля, созданного током в проводнике. Если ток течет по замкнутому проводнику (контурный ток), то направление вращения ручки буравчика совпадает с направлением тока в витке, тогда направление перемещения буравчика покажет направление вектора магнитной индукции, созданной током в витке на своей оси.

Чтобы определить направление силовых линий магнитного поля созданного током в прямом проводнике нужно охватить проводник правой рукой, направив отогнутый большой палец по направлению тока, кончики остальных пальцев в данной точке покажут направление вектора индукции в этой точке.

Из рисунков 1 б и в видно, что магнитное поле, созданное замкнутыми токами также, как и поле прямого тока неоднородно.

Если нужно получить однородное магнитное поле, то можно взять два соосно расположенных на близком расстоянии друг от друга витка с током. Между витками будет существовать довольно протяженная область пространства с однородным магнитным полем. ( рис. 1д).

Для получения однородного магнитного поля используют катушку в виде намотанного на цилиндрическую поверхность изолированного проводника, которые образуют винтовую линию. Такое устройство называют соленоидом или катушкой индуктивности. Если витки расположены вплотную или очень близко друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью (рис. 1д). Силовые линии магнитного поля поля соленоида выглядят примерно так, как показано на рис. 1 д.

В средней части внутри полости соленоида, длина которого значительно больше диаметра, магнитное поле направлено параллельно вдоль оси соленоида. Оно однородно в середине соленоида и спадает к его концам. В теории электромагнетизма для количественного описания явлений используют две векторные величины, характеризующие магнитные поля. Это вектор магнитной индукции и вектор напряженности магнитного поля 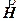. Для рассматриваемого нами случая, величина напряженности магнитного поля внутри соленоида Н пропорциональна силе тока I и определяется по формуле

H = I · n ₀ , (1)

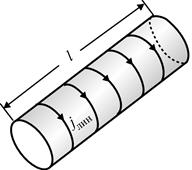
где n ₀ - число витков на единицу длины n ₀ = N / l (N – общее число витков соленоида, l – длина соленоида, рис. 2). Напряженность магнитного поля в системе СИ имеет размерность [А/м].

Вектор магнитной индукции 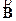связан с вектором напряженности магнитного поля 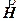выражением:

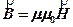, (2)

где m₀- так называемая магнитная постоянная (m₀= 4p´10^-7 Гн/м), m - безразмерная величина, характеризующая магнитные свойства среды и называемая относительной магнитной проницаемостью среды. Для вакуума μ = 1. Индукцию магнитного поля в единицах СИ измеряют в Теслах [Тл].

Величина индукции магнитного поля на оси длинного соленоида конечной длины (сравнительно с его диаметром) вычисляется по формуле

B = 0,5 mm₀In ₀(cosa₁ + cosa₂), (3)

где a₁ и a₂ - углы, под которыми видны концы соленоида из точки А на его оси, к которой относится величина В. В случае достаточно длинного соленоида, когда углы α₁ и α₂ близки к нулю, формула (3) приводится к виду: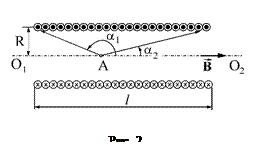

B = mm₀In ₀,

Простые соленоиды позволяют получать поля до 0,2 Тл. Соленоиды с охлаждением обмотки позволяют получать поля до 10 Тл. Через такой соленоид пропускается ток в десятки килоампер, а расход воды для охлаждения составляет сотни кубометров в секунду.

Внутри соленоида направление линий магнитной индукции образует с направлением тока в витках правовинтовую систему. Это позволяет использовать правило правой руки для определения направления силовых линий магнитного поля как это показано на рис. 1.

У реального соленоида имеется составляющая тока

Рис.1

вдоль оси. Кроме того, линейная плотность тока

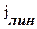(равная отношению силы тока dI к элементу длины соленоида) dlизменяется периодически при перемещении вдоль соленоида. Среднее значение этой плотности равно

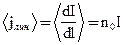
(4)

В учении об электромагнетизме большую роль играет воображаемый бесконечно длинный соленоид, у которого отсутствует осевая составляющая тока и, кроме того, линейная плотность тока 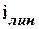постоянна по всей длине соленоида. Причина этого заключается в том, что поле такого соленоида однородно и ограничено объемом соленоида (аналогично электрическое поле плоского конденсатора, которое однородно и ограничено объемом конденсатора).



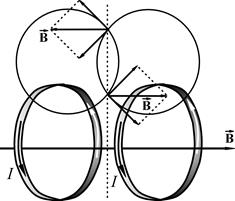
Рис. 3. Схематическое представление соленоида в виде тонкостенного цилиндра с постоянной плотностью тока j_лин		Рис. 4. Результирующее магнитное поле создаваемое парой соседних витков соленоида

В соответствии с выше сказанным можно представить соленоид в виде бесконечного тонкостенного цилиндра, обтекаемого током с постоянной линейной плотностью (рис. 3).

Разобьем цилиндр на одинаковые круговые токи - «витки». На рис. 4 видно, что каждая пара витков, расположенная симметрично относительно некоторой плоскости, перпендикулярной к оси соленоида, создает в любой точке этой плоскости магнитную индукцию, параллельную оси. Следовательно, и результирующее поле в любой точке внутри и вне бесконечного соленоида может иметь лишь направление, параллельное оси.

Рис.2

Из рис. 1 д вытекает, что направление поля внутри и вне конечного соленоида противоположны. При увеличении длины соленоида, направления полей не изменяются и в пределе, при l®¥ остаются противоположными. Для бесконечного соленоида, как и для конечного, направление поля внутри соленоида образует с направлением обтекания цилиндра правовинтовую систему.

Из параллельности вектора 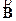оси соленоида вытекает, что поле как внутри, так и вне бесконечного соленоида должно быть однородным.

Поле как внутри, так и вне бесконечного соленоида является конечным. Причем, вне соленоида поле очень слабое и близко к нулевым значениям. Внутри бесконечно длинного соленоида магнитное поле значительно и определяется выражением:

B = m₀n ₀ I, (5)

где произведение n ₀ I называется числом ампер-витков на метр.

Если соленоид является конечным, то, как уже указывалось ранее, индукция магнитного поля в центре на оси соленоида определяется выражением (3).

В магнитную индукцию на оси соленоида симметрично расположенные витки вносят одинаковый вклад. Поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине значения в представленной формуле (5):

B = 0,5m₀n₀ I (6)

Практически, если длина соленоида значительно больше, чем его диаметр, формулы (5) и (6) будут справедливы с большой степенью точности.

Измерение индукции магнитного поля с помощью

Датчиков Холла

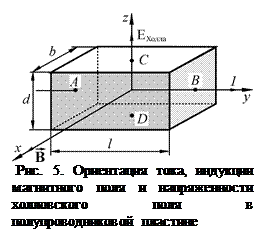
Эффект Холла заключается в следующем. Пусть образец имеет форму прямоугольной пластинки длиной l, шириной d , толщиной b (рис. 5). Если вдоль длины образца (направление оси у) пропустить электрический ток I, а перпендикулярно плоскости пластинки (направление оси х) приложить магнитное поле В, то в направлении, перпендикулярном направлению тока I и В (направление оси z), возникнет электрическое поле, называемое полем Холла, с напряженностью Е_Холла. На практике, как правило, поле Холла характеризуют разностью потенциалов, которую измеряют между симметричными токами C и D на боковых поверхностях образца. Эта разность потенциалов называется холловской разностью потенциалов (U_Холл или ЭДС Холла e_Холл ).

В классической теории проводимости эффект Холла объясняется тем, что в магнитном поле на движущиеся электрические заряды действует сила Лоренца, величина и направление которой определяются векторным уравнением

F_Л= e[v´B], (7 а)

где В — индукция магнитного поля, v — скорость движения зарядов, е — заряд носителей тока с учетом знака, «+е» - для дырочной проводимости, «-е» - для электронной проводимости.

Рассмотрим в качестве примера движение заряженной частицы в однородном поле. На движущуюся в магнитном поле на заряженную частицу будет действовать сила Лоренца (7 а). В скалярном виде выражение (7 а) имеет следующую запись:

F_Л= evB´sina, (7 б)

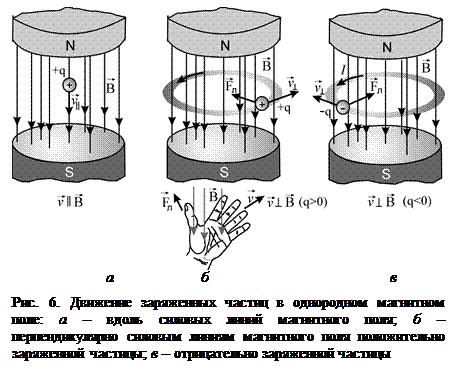где a - угол между векторами v и B. При движении заряд вдоль силовых линий магнитного поля (v êêB и sina=0), то он не испытывает действия силы Лоренца и его траектория является прямолинейной (рис. 6 а). В том случае, когда положительно заряженная частица движется перпендикулярно силовым линиям магнитного поля (v^ B и sina=1), сила Лоренца будет отклонять их нормально к вектору скорости (рис. 6 б). Сила Лоренца направлена перпендикулярно к плоскости, в которой лежат векторы v и B (рис. 6). Таким образом, под действием этой отклоняющей силы движение электронов приобретает более сложный характер, их траектория станет криволинейной. Для определения направления силы Лоренца применяют правило «левой руки»: если расположить левую руку так, чтобы силовые линии магнитного поля (вектор B ) входили в ладонь, а четыре сложенных пальца были направлены вдоль вектораскоростиv, то отставленный большой палец укажет направление силы Лоренца, действующей на положительный заряд (рис. 6). В случае, когда заряд отрицательный, найденное таким образом направление силы Лоренца нужно изменить на противоположное.

Направление силы Лоренца может быть также определено по правилу векторного произведения с учётом знака заряда. Вектор силы всегда перпендикулярен вектору скорости электрона. С учетом вышесказанного на рис. 7 представлено движение электрона под действием силы Лоренца в магнитном поле в металлической платине. Видно, что электроны при своем направленном движении в магнитном поле под действием силы Лоренца создадут на верхней пластине избыток отрицательных зарядов. Это в свою очередь приведет к тому, что нижняя пластина будет иметь положительный заряд.

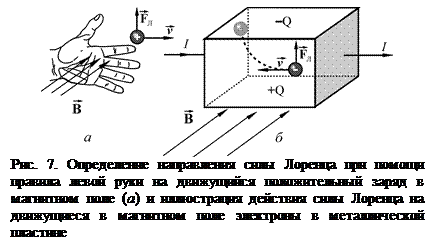С учетом этого явления электрическое поле, которое создается между верхней и нижней пластиной и получило название электрическое поле Холла :

Е_Холл = vB (8)

связано с ЭДС Холла e_Холл, или с холловской разностью потенциалов U_Холл, следующим образом:

e_Холл = U_Холл = Е_Холл´d = v´B´d . (9)

Так как сила тока, протекающего через единицу поверхности образца, т. е. плотность тока, равна

j=e´n´v, (10)

где п — число носителей тока в единице объема образца (концентрация носителей тока), то сила тока

I=j´b´d=e´n´v´b´d, (11)

что позволяет записать

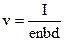
(12)

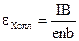. (13)

Таким образом, ЭДС Холла пропорциональна силе тока I через образец и обратно пропорциональна толщине образца b .

Экспериментальное определение ЭДС Холла e_Холл проводят на образце с заданной толщиной b при фиксированном токе через образец I. При этом полученное значение ЭДС Холла рассчитывают на единицу толщины образца и единицу силы тока, т. е. рассчитывают величину

e*_Холл =e*_Холл ´b/I , (14)

которую называют удельной или приведенной ЭДС Холла. Приведенная ЭДС Холла пропорциональна индукции магнитного поля В:

e*_Холл = R´B (15)

где коэффициент пропорциональности

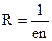(16)

является характеристикой изучаемого вещества и называется коэффициентом Холла или постоянной Холла.

Рассмотренный эффект Холла, причиной которого является действие на движущиеся в магнитном поле заряды силы Лоренца, называется классическим эффектом Холла. Как следует из формулы (15), для классического эффекта Холла характерна линейная зависимость e*(B). Опыт между тем показывает, что в природе есть вещества для которых линейная зависимость e*(В)не выполняется. Это свидетельствует о существовании другой причины эффекта Холла, которая, однако, может быть понята только с позиций квантовой теории твердого тела.

Описание экспериментальной установки

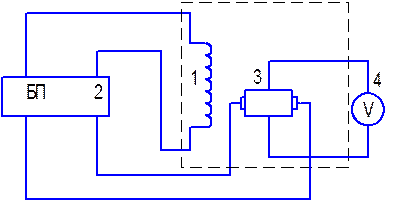
Принципиальная схема установки приведена на рис. 8. Соленоид 1 подключен к универсальному блоку питания 2. Соленоид имеет NNN витков, намотанных проводом диаметром 1.06 мм в два слоя, и имеет постоянную К_с, которую необходимо будет вычислить в Тл/А. Через соленоид протекает постоянный ток, величина которого задается с помощью регулятора, расположенного на передней панели блока питания, а измеряется амперметром, встроенным в блок питания.

Рис.8

Измерительный зонд "С" с встроенным датчиком Холла 3, с помощью которого измеряется величина магнитного поля внутри соленоида (миллитеслометр ТПУ) . Рабочая часть зонда "С" выполнена в виде стержня из немагнитного непроводящего материала, измерительный преобразователь Холла установлен на расстоянии 2 мм от торца так,что магниточувствительная ось преобразователя совпадает с продольной осью зонда.

При помощи зонда "С" измеряют составляющую вектора магнитной индукции, параллельную продольной оси зонда. Зонд укреплен на специальном держателе и находится внутри соленоида. Конструкция держателя позволяет перемещать зонд вдоль оси соленоида от одного его конца до другого. Держатель имеет линейку с ценой деления 10 мм.

Соленоид с зондом укреплен на специальной конструкции.

Дата добавления: 2021-01-21; просмотров: 614; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!