Алгоритм шифрования Эль-Гамаля

 

Схема была предложена Тахером Эль-Гамалем в 1984 г. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и обеспечения аутентификации. Стойкость данного алгоритма базируется на сложности решения задачи дискретного логарифмирования.

Суть задачи заключается в следующем. Имеется уравнение

g^x mod p = y. (9.6)

Требуется по известным g, y и p найти целое неотрицательное число x (дискретный логарифм).

Порядок создания ключей приводится в следующей таблице.

Таблица 9.8. Процедура создания ключей

№ п/п	Описание операции	Пример
1	Выбирается простое число p.	p = 37
2	Выбирается число g, являющееся первообразным корнем по модулю p и меньшее р.	g = 2
3	Выбираются произвольное число x, меньшее p.	x = 5
4	Вычисляется y = gx mod p	y = 25 mod 37 = 32 mod 37 = 32
5	Открытый ключ - y, g и p. Причем g и p можно сделать общими для группы пользователей. Закрытый ключ - x.

Примечание. Первообразный (примитивный) корень по модулю p – наименьшее положительное число g такое, что

g^φ(p) mod p = 1

и

gⁱ mod p ≠ 1, для 1 ≤ i < φ(p)

где φ(p) – функция Эйлера (т.к. р – простое число, то φ(p) = p - 1).

Проверка. При g = 2 и p = 37, φ(37) = 37 – 1 = 36.

2³⁶ mod 37 = 1;
2¹ mod 37 = 2 (≠ 1);
2² mod 37 = 4 (≠ 1);
2³ mod 37 = 8 (≠ 1);
2⁴ mod 37 = 16 (≠ 1);
...;
2³⁴ mod 37 = 28 (≠ 1);
2³⁵ mod 37 = 19 (≠ 1).

Для шифрования каждого отдельного блока исходного сообщения должно выбираться случайное число k (1 < k < p – 1). После чего шифрограмма генерируется по следующим формулам

a = g^k mod p, (9.7)

b = (y^k Т) mod p, (9.8)

где Т – исходное сообщение;
(a, b) – зашифрованное сообщение.

Дешифрование сообщения выполняется по следующей формуле

T = (b (a^x)^-1) mod p (9.9)

или

T = (b a^p-1-x) mod p, (9.10)

где (a^x)^-1 – обратное значение числа a^x по модулю p.

Пример шифрования и дешифрования по алгоритму Эль-Гамаля при k = 7 приведен в таблице, хотя для шифрования каждого блока (в нашем случае буквы) исходного сообщения надо использовать свое случайное число k.

Первая часть шифрованного сообщения – a = 2⁷ mod 37 = 17.

a^x = 17⁵ = 1419857, (a^x)^-1 = 2 (1419857 * 2 mod 37 = 1) или a^p-1-x = 17^37-1-5 ≈ 1.3928892 * 10³⁸.

Таблица 9.9. Пример шифрования по алгоритму Эль-Гамаля (при k = const)

Открытое сообщение, Т	Символ	А	Б	Р	А	М	О	В
	Код	1	2	18	1	14	16	3
Вторая часть шифрограммы, b = (327 * T) mod 37		19	1	9	19	7	8	20
Открытое сообщение, T = (b * 2) mod 37		1	2	18	1	14	16	3

Ввиду того, что число k является произвольным, то такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, т.к. у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение Т и ключ не определяют шифртекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины k для шифровки различных сообщений Т и Т’. Если использовать одинаковые k, то для соответствующих шифртекстов (a, b) и (a’, b’) выполняется соотношение b (b’)^-1 = Т (Т’)^-1 (mod p). Из этого выражения можно легко вычислить Т, если известно Т’.

Пример. Предположим злоумышленник перехватил зашифрованное сообщение С = ((a₁, b₁), (a₂, b₂), …, (a_n, b_n)), для которого использовалось одно и тоже случайное число k. Он знает один из блоков T_i = E_k1(C_i) или при известном открытом ключе (y, g, p) ему удалось подобрать k’, которое совпало с используемым при шифровании k. Например по второму варианту, для шифрования символа Х (Т' = 22) злоумышленник использовал k’ = 7 (равное k). Тогда, b(X) = b’ = (32⁷ * 22) mod 37 = 11, (b’)^-1 = 27, (Т’)^-1 = 32. Расшифрование перехваченного сообщения приведено в следующей таблице.

Таблица 9.10. Пример расшифрования перехваченного сообщения

Вторая часть перехваченной шифрограммы, b		19	1	9	19	7	8	20
L = (b * (b’)-1) mod p = (b * 27) mod 37		32	27	21	32	4	31	22
Вскрытое открытое сообщение, Т	Код, определяемый по уравнению (T * (T’)-1) mod p = L (Т * 32) mod 37 = L	1	2	18	1	14	16	3
	Символ	А	Б	Р	А	М	О	В

 

Алгоритм на основе эллиптических кривых

 

Использование эллиптических кривых для создания криптосистем было независимо предложено Нилом Коблицем (Neal Koblitz) и Виктором Миллером (Victor Miller) в 1985 г. [8, 17]. При использовании алгоритмов на эллиптических кривых полагается, что не существует быстрых алгоритмов для решения задачи дискретного логарифмирования в группах их точек. В настоящий момент известны лишь экспоненциальные алгоритмы вычисления обратных функций для эллиптических кривых. По сравнению с субэкспоненциальными алгоритмами разложения числа на простые сомножители (см. криптосистему RSA), это позволяет при одинаковом уровне стойкости уменьшить размерность ключа в несколько раз, а, следовательно, упростить программную и аппаратную реализацию криптосистем.

Эллиптической кривой E называется множество точек (x, y), удовлетворяющих однородному уравнению Вейерштрасса:

y² + a₁xy + a₂y = x³ + a₃x² + a₄x + a₅, (9.11)

где a_i - коэффициенты уравнения.

е a_i - коэффициенты уравнения.

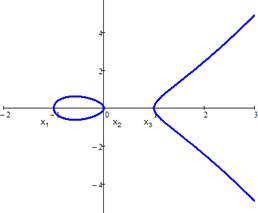
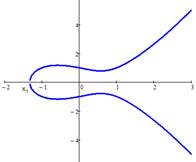
а) y2 = x3 – x	б) y2 = x3 – 3x + 2	в) y2 = x3 – x + 1

Рис.9.1. Примеры эллиптических кривых

В криптографии эллиптические кривые рассматриваются над двумя типами конечных полей: простыми полями нечётной характеристики (ℤ_n, где n > 3 - простое число) и полями характеристики 2 (GF(2^m)).

Эллиптические кривые над полями нечётной характеристики ℤ_n можно привести к виду, называемому эллиптической кривой в короткой форме Вейерштрасса:

y² = x³ + Ax + B (mod n), (9.12)

где A, B ℤ_n - коэффициенты эллиптической кривой, удовлетворяющие 4 A³ + 27 B² ≠ 0 (mod n).

Поскольку , график кривой симметричен относительно оси абсцисс. Чтобы найти точки его пересечения с осью абсцисс, необходимо решить кубическое уравнение

x³ + Ax + B = 0. (9.13)

Это можно сделать с помощью известных формул Кардано. Дискриминант этого уравнения

. (9.14)

Если ∆ > 0, то уравнение имеет три различных действительных корня (см. рис. 9.1а – x₁, x₂ и x₃). Если ∆ = 0, то уравнение имеет три действительных корня, по крайней мере, два из которых равны (см. рис. 9.1б – x₁ и x₂). Если ∆ = 0, то уравнение имеет один действительный корень (см. рис. 9.1в – x₁) и два комплексно сопряженных.

Используемые в криптографии кривые не должны иметь особых точек. Геометрически это значит, что график не должен иметь точек возврата и самопересечений (см. рис. 9.1б). Если кривая не имеет особых точек, то её график имеет две части при положительном дискриминанте (см. рис. 9.1а), и одну - при отрицательном (см. рис. 9.1в). Например, для графиков выше в первом случае дискриминант равен 64, а в третьем он равен -368.

Следует отметить, что в ℤ_n у каждого ненулевого элемента есть либо два квадратных корня, либо нет ни одного, поэтому точки эллиптической кривой разбиваются на пары вида P = (x, y) и -P = (x, -y). Например, эллиптическая кривая y² = x³ + 3x + 2 при x = 1 и n = 5 имеет две точки в качестве решения: P = (1, 1) и -P = (1, -1), т.к. 1² ≡ 1³ + 3 * 1 + 2 (mod 5) и (-1)² ≡ 1³ + 3 * 1 + 2 (mod 5).

Введем две операции, которые можно выполнять над точками кривой.

Сложение точек P₃(x₃, y₃) = P₁(x₁, y₁) + P₂(x₂, y₂).

а) y2 = x3 – x	б) y2 = x3 – x + 1

Рис.9.2. Сложение точек

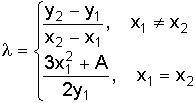(9.15)

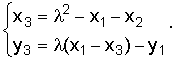(9.16)

В формулах 9.15 и 9.16 λ - угловой коэффициент прямой, проходящей через точки P₁ и P₂. Если P₁ = P₂, то λ равен значению производной в точке P₁.

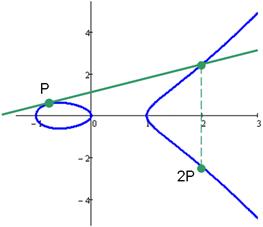
Умножение точки на число P_k(x_k, y_k) = k * P(x, y).

а) y2 = x3 – x	б) y2 = x3 – x + 1

Рис.9.3. Удвоение точки

А) вариант 1 – выполнить сложение точки P k раз

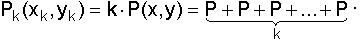(9.17)

B) вариант 2 – с использование двоичного представления числа k = (b_L, …, b₂, b₁) и операции удвоения точки. Например, k = 110₁₀ = 1101110₂, тогда P_k = 64P + 32P + 8P + 4P + 2P.

Алгоритм, вычисления P_k может выглядеть следующим образом.

P_k = null, Q = P.
for i = 1 to L
If b_i = 1
then if P_k = null
then P_k = Q
else P_k = P_k + Q
Q = 2 * Q (≈ Q = Q + Q)
endFor

Для k = 110 вместо 109 сложений будет 1 присваивание, 4 сложения и 6 удвоений (сложений).

Рассмотрим процедуру создания ключей.

Таблица 9.11. Процедура создания ключей

№ п/п	Описание операции	Пример
1	Выбирается модуль эллиптической кривой - простое число n (n > 2255 - ГОСТ).	n = 41
2	Выбираются коэффициенты эллиптической кривой A и B. Должно соблюдаться условие (4 A3 + 27 B2) mod n ≠ 0, в противном случае меняются параметры эллиптической кривой n, A или B.	A = 3, B = 7 (4 * 33 + 27 * 72) mod 41 = 37
3	Определяется точка эллиптической кривой P(xp, yp) и порядок циклической подгруппы группы точек эллиптической кривой q*). Принимается произвольное xp (0 < xp < n) и определяется yp из уравнения эллиптической кривой. Должны соблюдаться условия: - для xp должен существовать yp (не для всякого xp при данных параметрах кривой (A, B, n) может существовать yp); - P ≠ O и q P = O, где O - нулевая точка эллиптической кривой (P + (-P) = O); - q – простое число; - nt mod q ≠ 1, для всех целых t = 1, 2, …, T, где T ≤ 31; - 2254 < q < 2256 (ГОСТ) в противном случае меняются либо параметры эллиптической кривой n, A или B либо выбирается другая точка P.	xp = 7 ((73+3*7+7) mod 41 = 2), yp = 17 (172 mod 41 = 2) q = 47
4	Выбирается закрытый ключ d (0 < d < q).	d = 10
5	Определяется точка эллиптической кривой Q(xq, yq): Q(xq, yq) = d * P(xp, yp).	xq = 36, yq = 20
6	Публикуется открытый ключ [(A, B), P(xp, yp), n, Q(xq, yq)] в специальном хранилище, где исключается возможность его подмены (общедоступном сертифицированном справочнике). Для выработки и проверки электронной цифровой подписи q является частью открытого ключа вместо n.

*) Прямой способ вычисления порядка группы точек эллиптической кривой q.

1) Рассчитываются координаты первой точки из выражения

y² = x³ + Ax + B (mod n) > y² = x³ + 3x + 7 (mod 41).

Примем x₁ = 7, тогда y₁² mod 41 = (7³ + 3 * 7 + 7) mod 41 = 2, откуда y₁ = 17.

P(x_p, y_p) = P(x₁, y₁) = P(7, 17).

2) Находим координаты второй точки. Для этого вначале вычисляется коэффициент λ

Решая последнее уравнение, получаем λ = 2 (34 * 2 mod 41 = 27).

Координаты второй точки получаем путем удваивания первой из выражений

x₂ = (λ² – 2x₁) mod n = (2² – 2 * 7) mod 41 = -10 mod 41 = 31,

y₂ = (λ(x₁ – x₂) – y₁) mod n = (2 (7 – 31) – 17) mod 41 = -65 mod 41 = 17.

3) Каждую следующую точку рассчитываем по формулам, пока в знаменателе первой формулы не будет получен 0:

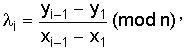(9.18)

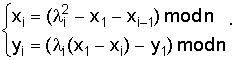(9.19)

Получаем:

- λ₃ = 0, x₃ = 3, y₃ = 24;

- λ₄ = 29, x₄ = 11, y₄ = 31;

- λ₅ = 24, x₅ = 25, y₅ = 2;

- …;

- λ₄₆ = 2, x₄₆ = 7, y₄₆ = 24.

К полученному числу точек добавляем точку О, в результате чего q = 46 + 1 = 47. Эта точка есть результат сложения любых двух точек P(x_i, y_i) и -P(x_i, -y_i) и представляет собой бесконечно удаленную точку, в которой гипотетически сходятся все вертикальные кривые.

Процедура шифрования отдельного блока выполняется следующим образом [25].

Таблица 9.12. Процедура шифрования отдельного блока (буквы)

№ п/п	Описание операции	Пример
1	Определяется десятичное представление буквы t.	Буква «K» t = 12
2	Выбирается случайное число k (0 < k < n).	k = 5
3	Определяется точка Pk(xpk, ypk) = k * P.	Pk(25, 2)
4	Определяется точка Qk(xqk, yqk) = k * Q.	Qk(3, 24)
5	Вычисляется с = (t * xqk) mod n.	с = (12 * 3) mod 41 = 36
6	Шифрограмма – пара [Pk, c].	[Pk(25, 2), 36]

Процедура расшифрования отдельного блока выполняется следующим образом.

Таблица 9.13. Процедура расшифрования отдельного блока (буквы)

№ п/п	Описание операции	Пример
1	Вычисляется точка D(xd, yd) = d * Pk.	D(3, 24)
2	Вычисляется десятичное представление зашифрованной буквы t = (с * xd-1) mod n, где xd-1 – обратное число к xd по модулю n.	xd-1 = 14 [(3 * 14) mod 41 = 1] t = (36 * 14) mod 41 = 12
3	Определяется исходное сообщение по ее десятичному представлению.	Буква «K»

Приведенный выше способ шифрования является вариацией шифрования Эль-Гамаля. Если стойкость алгоритма шифрования Эль-Гамаля базируется на сложности решения задачи дискретного логарифмирования, то стойкость шифрования с помощью эллиптических кривых базируется на сложности нахождения множителя k точки P по их произведению. Т.е. если Q = k P, то зная P и k довольно легко вычислить Q. Эффективное решение обратной задачи (найти k при известных P и Q) на текущий момент пока не опубликовано.

В лабораторной работе необходимо зашифровать свою фамилию с помощью следующих шифров:

- алгоритма RSA;

- алгоритма на основе задачи об укладке ранца;

- алгоритма шифрования Эль-Гамаля.

При оформлении отчета необходимо привести исходное сообщение (фамилию) и таблицы генерации ключей, шифрования и расшифрования. Для первого и третьего способов принять, что код символа соответствует его положению в алфавите, для второго – в соответствии с кодировкой Windows 1251.

 

 

---

Дата добавления: 2021-01-21; просмотров: 2205; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!