Оценка параметров уравнения регрессии при ПЛР

Моделирование Лекция 3

Основные процедуры математического моделирования

Аппроксимация

Аппроксимация, или приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.

В математическом моделировании аппроксимация используется в двух вариантах:

1) имеются экспериментальные данные, отражающие объективную реальность, в виде отдельных точек и требуется представить их виде гладкой функции, которая и будет математической моделью, отражающей эти объективные экспериментальные данные;

2) уже имеется некая исходная математическая модель, но необходимо создать такую математическую модель, которая с одной стороны будет проще исходной, а с другой стороны будет похожа (в определённых рамках) на нее.

В общем случае выбор аппроксимирующей функции во многом определяется физикой описываемого процесса.

Часто задача аппроксимации сводится либо к линеаризации, либо к линейной регрессии.

Математика многогранна и в ней можно найти как математическую модель, внутри которой имеется блок аппроксимации, так и аппроксимацию целой математической модели. Если первое понятно и пояснений не требует, то примером второго является, например, аппроксимация редкого катастрофического явления, где само явление описывается сложной математической моделью.

Линеаризация

Выгоды линейности бывают столь велики, что приближенная замена нелинейных соотношений на линейные, нелинейных моделей на линейные, т. е. линеаризациясоотношений, моделей и т. д. весьма распространена в моделировании.

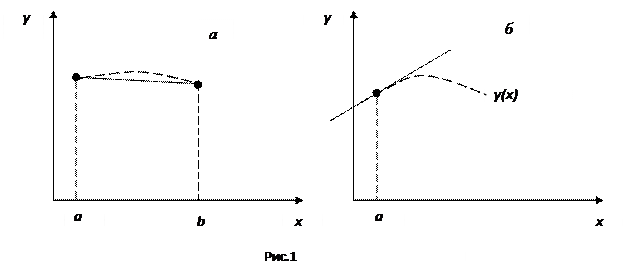
Рассмотрим вначале два наиболее часто используемых случаев линеаризации: либо если эксперимент показывает (как, например, для закона Гука), что отклонение от линейности в рассматриваемом диапазоне ab изменения переменных невелико и несущественно (рис.1,а), либо же необходимо линеаризовать функцию в окрестности точки a (рис.1,б).

В первом случае используется линейная интерполяция, а во втором – линеаризация с применением ряда Тейлора.

Линейная интерполяция

Задача сводится к нахождению прямой, проведенной через две точки:

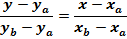
, (1)

откуда 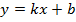, где

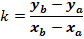
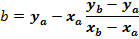
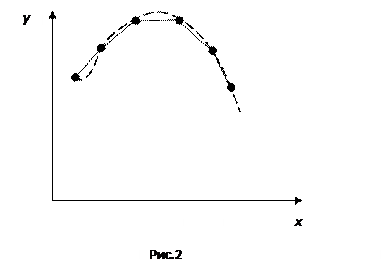
В общем случае линейную интерполяцию можно применить и для большего количества точек – в этом случае вместо кривой линии получаем ломаную линию, состоящую из последовательно соединенных прямых линий (рис.2).

Линеаризация с помощью ряда Тейлора

В этом случае функция y ( x ) раскладывается в ряд Тейлора в окрестности точки a (рис.1,б):

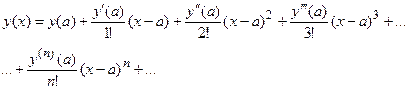
с отбрасыванием всех членов высшего порядка малости (в этом и состоит линеаризация):

, (2)

где .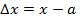

Второе слагаемое в (2) – дифференциал функции y ( x ) в точке a.

Пример. Исходная математическая модель является квадратным трехчленом:

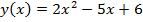. (3)

Необходимо линеаризовать эту модель в окрестности точки x=2.

Решение. По (3) находим: 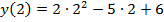=4. Производная

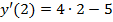в точке x=2 равна: =3, тогда линеаризованная модель

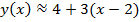. (4)

Сравним результаты расчетов по формулам (3) и (4):

Таблица 1

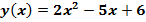
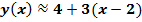
x			Относительная погрешность ,%
2	4	4	0
2.01	4,03	4,03	0
2,04	4,123	4,12	0,07
2,1	4,32	4,3	0,46
2,5	6	5,5	8,3

Как видим, при малых отклонениях погрешности получаются незначительными.

К тому же, модель (4) проще, чем (3), но недостатком такого подхода является необходимость пересчета коэффициентов (фактически построение другой модели) при существенном изменении значения x (например, при x=3).

Линейная регрессия

Общие положения

Как мы видели, математическая статистика занимается обработкой данных, полученных в результате какого-либо эксперимента. В частности – это зависимость величины Y от величины X в виде набора точек на плоскости (x_i , y_i), i = 1, …, n (рис.3). Но эта зависимость не будет однозначной (т.е. функциональной), а будет вероятностной (или стохастической), поскольку в общем случае и Y и X – случайные величины.

Функциональные связи являются абстракциями, в реальной жизни онивстречаются редко, но находят широкое применение в точных науках и впервую очередь, в математике. Например: зависимость площади круга отрадиуса: S=π∙r²

Обычно при стохастической зависимости между X и Y одна величина рассматривается как независимая (X), а вторая (Y) – как зависимая от первой, и зависимая величина ведет себя как случайная величина и ее можно описать некоторым вероятностным законом распределения.

Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.

Учитывая специфику вероятностной связи, эти величины (точнее – признаки) чаще называют факторными (которые обуславливают изменения других), или просто факторами, и результативными (которые изменяются под действием факторных признаков).

Возникновение понятия стохастической зависимости обусловливается тем, что величины подвержены влиянию неконтролируемых или неучтённых факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.То есть изучаемая система переходит не в определенное состояние, а в одно из возможных для нее состояний. Стохастическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения.

Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Поэтому при проведении того же эксперимента мы могли бы получить и несколько другой набор пар (x_i , y_i) (точки красного цвета нарис.4) в силу именно случайности фигурирующих в эксперименте величин.

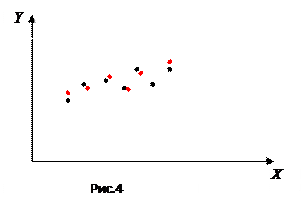Это можно интерпретировать, что рис.3, например, является своего рода «фотографией», а на самом деле точки (x_i , y_i), в силу случайных факторов, могут занимать и другое место на графике.

Модель стохастической связи может быть представлена в общем виде уравнением: ŷ_i = ƒ(x_i) + e_i, где:

f(x_i)-часть результативного признака, сформировавшаяся под воздействием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;
ŷ_i-расчетное значение результативного признака;
e_i-часть результативного признака, возникшая вследствие действия неконтролируемых или неучтенных факторов, а также измерения признаков, неизбежно сопровождающегося некоторыми случайными ошибками.

Сравним: модель функциональной связи:

Разные разделы математической статистики посвящены обработке случайных величин в соответствии с разными задачами, например, с точки зрения расчета параметров выборки, или - отличия выборочных параметров от параметров генеральной совокупности, и т.д. Регрессионный анализ (РА) является тоже разделом математической статистики и в нем обрабатываются случайные величины со своих позиций, а именно:

регрессионный анализ устанавливает формы зависимости между этими величинами X и Y . Такая зависимость определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров (красные линии на рис.5).

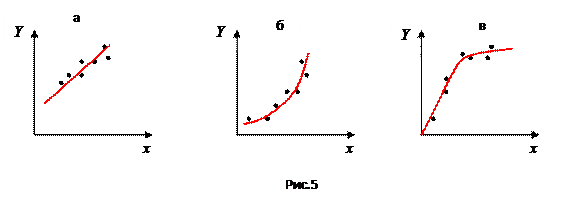Наиболее общая задача РА: для экспериментальных данных, имеющих между собой стохастическую зависимость, подобрать наиболее адекватную математическую модель в виде уравнения регрессии, графически являющейся некоторой линией.

Отметим, что при изучении стохастических зависимостей кроме РА используют и корреляционный анализ.

Фразу «наиболее адекватную математическую модель» нужно понимать в соответствии со следующими положениями.

Для каждого конкретного значения x_i, кроме зафиксированного значения y_i величины Y, имеется также несколько других значений величины Y (в силу ее случайности): y_i ₁ , y_i ₂ , y_i ₃ ,… y_in, поэтому можно говорить о среднем значении:

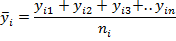
(5)

В итоге для каждого x_i имеется свое значение :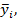

Таблица 2

x₁	x₂	x₃	…	x_n
			…

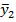
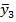
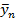
Если величина x не является случайной (через строчную букву обозначаются именно неслучайные величины), то зависимость по табл.2 является однозначной и искомой. В наиболее строгом варианте речь идет о некой генеральной совокупности, где между значениями Y и x имеется зависимость, а конкретно - зависимость между МО величины Y и величиной x, отражением которой является табл.2. Но дело в том, что эта зависимость имеет теоретическое значение, поскольку мы не знаем всей совокупности значений y_i ₁ , y_i ₂ , y_i ₃ ,… y_in, однако наиболее близкое к ней уравнение регрессии и будет наиболее адекватным.

Регрессия – это зависимость среднего значения (точнее – математического ожидания) случайной величины Y от величины x .

В РА рассматривается и вариант, когда величина X является случайной (через заглавные буквы обозначаются случайные величины), тогда речь будет идти о зависимости среднего значения случайной величины Y от среднего значения величины X (мое –проверить).

РА состоит из нескольких этапов:

§ выбор уравнения регрессии (математической модели);

§ оценка неизвестных параметров этой модели;

§ определяются статистические ошибки оценки или границы доверительных интервалов;

§ проверяется адекватность принятой математической модели экспериментальным данным.

Простая линейная регрессия

Простая линейная регрессия (ПЛР) имеет место в случае, когда зависимая величина Y определяется одной величиной x. В этом случае ПЛР выражается уравнением (рис.6):

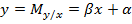(6)

Здесь 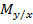означает, что МО случайной величины Y определяется при фиксированном значении величины x.

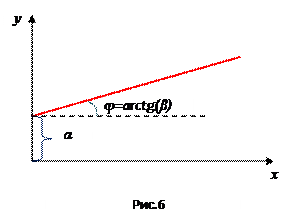
Основное предположение ПЛР:

В генеральной совокупности, из которой получены экспериментальные данные, действительно существует линейная регрессия, т.е. 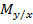зависимой случайной величины Y для любого значения независимой величины x является линейной функцией вида (6).

Пример 1 ПЛР. (из учебника Иванова). Мировые рекорды в прыжках с шестом:

Рис.7

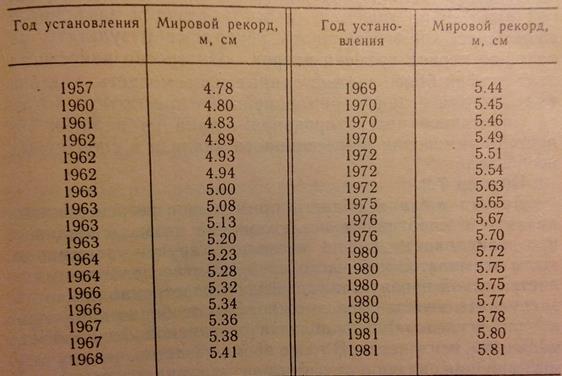
В виде графика:

Рис.8

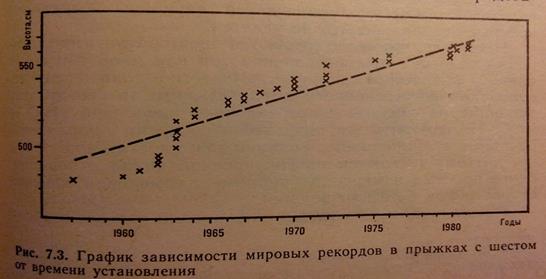
Заманчиво: можно сделать прогноз (проверить!).

Оценка параметров уравнения регрессии при ПЛР

Истинное уравнение ПЛР , отображаемое в общем виде, в частности, таблицей 2, неизвестно (всю генеральную совокупность наблюдать невозможно). Можно только по имеющейся выборке экспериментальных данных оценить генеральные параметры α и β.

Итак, имеется экспериментально определенная выборка объема n , представляющая собой пары ( x_i ; y_i ) - наблюдений зависимой величины Y , соответствующей значениям независимой переменной x .

Оценки генеральных параметров α и β обозначаются соответственно a и b:

(7)

соответственно, 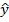- это оценка.

Для их определения чаще всего используется метод наименьших квадратов (МНК).

Отметим, что, как показано на рис.9, прямую через экспериментальные данные можно провести по разному.

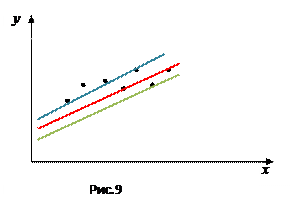Суть МНК заключается в следующем: искомая функция (7) должна быть построена так, чтобы сумма квадратов отклонений (рис.10) у- координат всех экспериментальных точек от у- координат графика функции была бы минимальной, то есть рассматривается для каждой точки разность отмеченных у- координат:

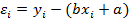(8)

Тогда минимизируемая сумма запишется в виде функции:

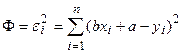(9)

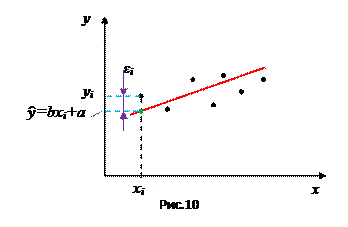
Почему сводятся к минимуму квадраты ошибок, а не сами ошибки? Дело в том, что в большинстве случаев ошибки бывают в обе стороны: оценка может быть больше измерения или меньше его. Если складывать ошибки с разными знаками, то они будут взаимно компенсироваться, и в итоге сумма даст нам неверное представление о качестве оценки. Часто для того, чтобы итоговая оценка имела ту же размерность, что и измеряемые величины, из суммы квадратов ошибок извлекают квадратный корень.

Далее находится минимум выражения (9). Для этого приравнивают к нулю частные производные 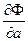и , и 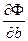получают формулы для нахождения неизвестных коэффициентов:

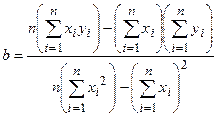
(10)

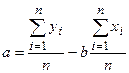
(11)

Если уравнение прямой ищется в виде y = bx, то верна следующая формула:

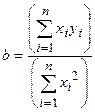
(12)

Пример

Данные экспериментальных исследований:

x	1,5	1,9	2	2,3	2,5	2,8	3
y	4	4,4	2,7	2,3	0,3	-0,5	-0,9

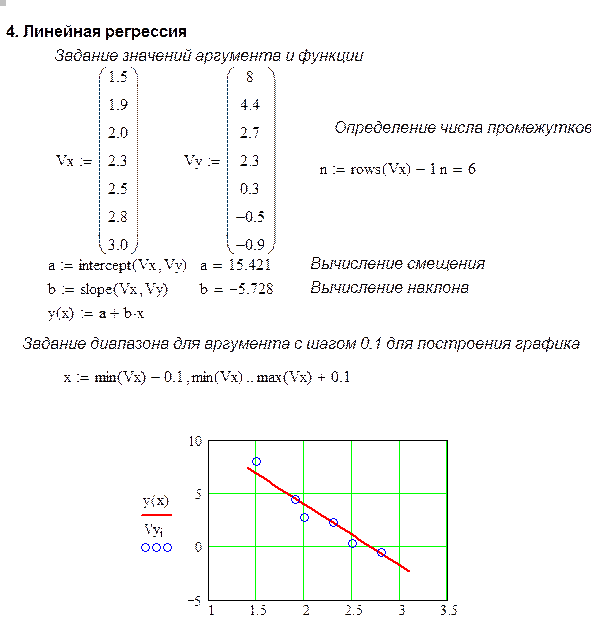
Таким образом, искомая прямая имеет вид : ,

Подбор эмпирической формулы

Остановимся особо на вопросе о подборе эмпирической формулы для функциональной зависимости между величинами. Пусть мы знаем, что некоторая величина у является функцией другой величины л:, т. е. у = у(х), но аналитическое выражение этой функции нам неизвестно и мы хотим подобрать для нее формулу у = fix), с достаточной для нас точностью описывающую зависимость. Пусть, далее, в результате эксперимента или наблюдения, мы получили ряд значений х и соответствующих значений у:

Тогда, если N не слишком велико, обычно начинают с нанесения этих данных на координатную ось в виде отдельных точек. При этом становятся видны точки, выпадающие из общего хода зависимости. Они могут свидетельствовать о каких-то важных эффектах, требующих специального исследования, но чаще получаются из-за существенных ошибок при эксперименте или вычислениях — тогда эти точки просто игнорируются. Затем надо выбрать вид формулы, которой мы будем пользоваться. Если этот вид не вытекает из каких-либо общих соображений, то обычно выбирают одну из простейших элементарных функций или их простую комбинацию (сумму степенных или показательных функций и т. п.); конечно, для этого надо хорошо представлять себе возможные графики таких функций. При этом следят за тем, чтобы подбираемая функция fix) имела те же характерные особенности, что и изучаемая функция у(х). Так, если по своему содержательному смыслу функция у(х) четная, то и функция fix) должна быть четной и т. п.; очень важно правильно передать поведение функции при больших и малых значениях х, возможную смену ее знака и другие ее существенные черты. На малом интервале изменения х часто применяют наиболее простую — линейную функцию, а

вблизи точки экстремума — квадратичную функцию. Иногда не удается подобрать единую формулу на всем интервале изменения х и приходится разбивать этот интервал на части и на каждой подбирать свою формулу. После выбора вида формулы нужно определить значения входящих в нее параметров. Рассмотрим сначала случай, когда экспериментальные точки подсказывают линейную зависимость у от х, т. е. мы полагаем fix) = ах + b и нам надо найти значения параметров а и А. Если высокой точности не требуется (тем более, что формула все равно приближенная), то это можно сделать непосредственно с помощью графика, проведя прямую — лучше всего применив прозрачную линейку,— к которой экспериментальные точки лежат ближе вс^го, а затем определить ее параметры. Если требуется бблыыая точность или если мы хотим обойтись без геометрических построений, ограничившись линейными приближениями, то наиболее часто для подбора параметров а я b применяется метод наименьших квадратов. Он состоит в минимизации суммы квадратов разностей между эмпирическими значениями функции и соответствующими ее значениями, полученными из

Дата добавления: 2021-01-21; просмотров: 46; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!