ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНОЙ САР ЧАСТОТЫ ВРАЩЕНИЯ ТУРБОПРИВОДА
Учебное пособие
Самара 1998
-3-
СОДЕРЖАНИЕ
Предисловие................................................................................................................ 4
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
НЕЛИНЕЙНЫХ САР................................................................................................ 6
1.1. Особенности нелинейных САР........................................................................ 6
1.2. Методы исследования нелинейных САР..................................................... 7
1.2.1. Метод фазовых траекторий ............................................................. 9
1.2.2. Метод гармонической линеаризации............................................ 18
1.2.3. Теорема Ляпунова об устойчивости САР..................................... 32
1.2.4. Анализ устойчивости нелинейной САР частотным методом В.М Попова 43
2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНОЙ САР ЧАСТОТЫ
ВРАЩЕНИЯ ТУРБОПРИВОДА......................................................................... 48
2.1. Назначение и принцип действия САР............................................... 48
2.2. Вывод уравнений звеньев САР............................................................ 50
2.3. Определение параметров автоколебаний в САР алгебраическим способом 63
2.4. Исследование устойчивости и автоколебаний в САР частотным методом (методом Гольдфарба) 67
2.5. Моделирование САР с помощью пакета программ СИАМ. Оценка результатов исследования САР 70
Библиографический список.................................................................................... 74
Приложение 1. Коэффициенты гармонической линеаризации основных
нелинейных элементов САР .................................................................................. 75
Приложение 2. Задачи для самостоятельного решения................................ 77
-4-
Предисловие
При проектировании систем автоматического регулирования (САР) энергетических установок (ЭУ) различного назначения важным является учет как можно большего числа факторов, оказывающих влияние на их динамические свойства. К одним из таких существенных факторов относится нелинейность характеристик элементов САР, не учет которой может привести к качественно неверным результатам. Исследование характеристик нелинейных систем осложнено тем, что до сих пор не разработаны аналитические методы решения нелинейных дифференциальных уравнений и общем виде. Поэтому разработаны специальные методы изучения динамических свойств нелинейных САР, некоторые из которых рассматриваются в данном учебном пособии. Изучение этих методов япляси-.м непременным условием при подготовке высококвалифицированных специалистов, способных разрабатывать и грамотно эксплуатирован, агрегаты и системы ЭУ.
Как известно из теории автоматического регулирования, при исследовании динамики САР их разбивают на ряд взаимосвязанных звеньев. Учитывая то , что линейные методы более просты и достаточно отработаны, стремятся описать звенья линейными уравнениями, что является идеализацией при описании реальных устройств. При линеаризации характеристик звеньев в некоторых случаях теряются их существенные особенности. В качестве примера можно привести возникновение автоколебаний, непредсказуемых с точки зрения линейной теории систем. Изучение автоколебаний и разработка мероприятий по их предотвращению имеют важное значение при создании точных и надежных САР ЭУ.
-5- -
В учебном пособии изложены основы исследования устойчивости и
автоколебаний в нелинейных САР. Основное внимание уделено методу
гармонической линеаризации, или методу Гольдфарба, как получившему
наибольшее практическое применение. Подробно рассмотрен пример
исследования САР турбопривода, содержащей нелинейный струйный
усилитель. Для данной САР тремя различными методами (алгебраическим,
частотным, а также непосредственно моделированием на ПЭВМ) определены
параметры автоколебаний, дан анализ сходимости результатов.
Моделирование САР производилось с помощью пакета программ СИАМ (Система автоматизированного моделирования), позволяющего в диалоговом режиме набрать структурную схему нелинейной САР и построить ее характеристики.
-6-
1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ САР
1.1. Особенности нелинейных САР
Нелинейными называются системы, содержащие хотя бы один элемент, линеаризация уравнения которого разложением в ряд Тейлора невозможна без потери существенных свойств САР. Процессы в нелинейных САР описываются системой нелинейных дифференциальных уравнений. Для таких систем неприменим принцип суперпозиции или наложения сигналов, т.е. если
Хвых1 = f ( X вх1), Хвых2 = f ( X вх 2), то ХВЫХ1 + Хвых2 = f ( XBxl + Хвх2).
Переходные и частотные характеристики нелинейных САР в отличие от линейных зависят от амплитуды входного сигнала и тем в большей степени, чем существеннее нелинейность элементов.
Для нелинейных САР характерен режим автоколебаний самоустанавливающихся незатухающих колебаний, амплитуда и частота которых полностью определяются свойствами системы. Автоколебания приводят к преждевременному износу и разрушению элементов САР, к уводу характеристик систем с рабочей линии и являются нежелательными . Изучение автоколебаний и разработка мероприятий по их предупреждению имеют большое значение для повышения точности и надежности систем.
Изучение процессов в нелинейных САР затруднено тем, что до настоящего времени не разработаны общие методы решения нелинейных дифференциальных уравнений. Поэтому при исследовании характеристик нелинейных САР применяют численные и приближенные методы.
Изучение нелинейных САР начинается с описания характеристик нелинейных элементов. Рассмотрим характеристики типичных для САР
-7-
нелинейных элементов. Одним из самых распространенных нелинейных элементов САР является звено релейного типа (рис. 1.1 ,а,б). При непрерывном изменении входной величины происходит скачкообразное изменение выходного сигнала. Звеном с такой характеристикой является элемент с сухим трением, в котором входной величиной является скорость движения, а выходной - сила трения. Характеристика на рис. 1.2,а соответствует элементу с люфтом или с зоной нечувствительности, а на рис. 1.2,6 - элементу с насыщением, например, пневматическому или гидравлическому усилителю. Криволинейная характеристика на рис. 1.3,а соответствует гидравлическому дросселю, причем входной величиной является перепад давления, а выходной -расход жидкости. При малых отклонениях хвх от установившегося значения на одной из ветвей кривой она может быть линеаризована разложением нелинейной функции в ряд Тейлора. Однако, если дроссель размещен в тупиковой гидравлической цепи с возвратно-поступательным движением жидкости, то линеаризация его характеристики приводит к неверному результату при исследовании нелинейной САР. В элементах с гистерезисом (рис. 1.3,6) одному и тому же значению \ш могут соответствовать два значения хвых. Поэтому при математическом описании такого элемента следует учитывать помимо координаты хях знак скорости его изменения во времени. Гистерезисной характеристикой обладают механические демпфирующие элементы. Для них чем больше площадь петли гистерезиса, тем больше потери колебательной энергии. Гистерезисной характеристикой обладают также электромагнитные элементы САР.
1.2. Методы исследования нелинейных САР
В теории автоматического управления разработаны точные и приближенные методы исследования нелинейных САР. Точные методы разработаны академиком Андроновым А.А. и его учениками (1945 - 1950 гг.). К
|
|
-8-
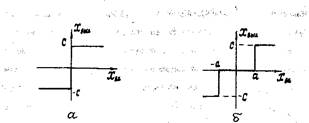
Рис. 1.1. Релейные характеристики нелинейных звеньев

Рис.1.2. Кусочно-линейные характеристики нелинейных звеньев
|
|
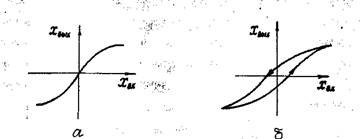
Рис. 1.3. Криволинейные характеристики нелинейных звеньев
-9-
точным методам относятся метод фазовых траекторий - для исследования САР не выше третьего порядка, метод припасовывания - для решения задач с нелинейными характеристиками элементов, сводимыми к кусочно-линейным характеристикам. Из приближенных методов широко применяется метод гармонического баланса, разработанный в 1937 г. академиками Крыловым Н.М. и Боголюбовым Н.Н. применительно к задачам радиотехники и позднее использованный Гольдфарбом Л.С. для решения некоторых задач автоматического регулирования. Дальнейшее развитие этот метод получил в работах Попова Е.П. и других ученых.
Метод фазовых траекторий
Состояние САР определяется значением регулируемого параметра и его п-1 производными, где а - порядок характеристического уравнения системы. Для САР второго порядка состояние системы будет определяться регулируемым параметром и скоростью его изменения. При этом состояние системы можно представить точкой на плоскости, называемой фазовой, по осям координат которой отложены регулируемый параметр и его первая производная. Точка на фазовой плоскости называется изображающей, а ее траектория движения, характеризующая динамику САР, - фазовой траекторией.
Начальные условия определяются начальным положением изображающей точки на фазовой плоскости. Совокупность фазовых траекторий, построенных при различных начальных условиях с особыми точками, составляет фазовую картину или фазовый портрет системы.
Метод фазовых траекторий для простоты рассмотрим на примере линейной САР второго порядка, свободное движение которой описывается уравнением
- 10-
' , J ' i "-! .,;-.,•
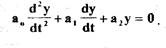 (1.1)'
(1.1)'
Представим уравнение (1.1) в виде двух равенств:
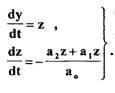 (1.2)
(1.2)
Разделив в (1.2) одно уравнение на другое, освободимся от 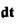 и получим
и получим
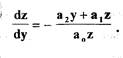 (1.3)
(1.3)
Уравнением (1.3) описывается фазовая траектория системы на фазовой плоскости. Для построения фазовой траектории вначале выбирают 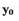 и
и 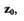
соответствующие начальным условиям (точка 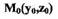 на рис. 1.4). По
на рис. 1.4). По
формуле (1.3) определяют направление касательной
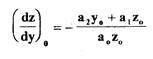
и проводят через точку 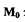 эту касательную. Следующую точку
эту касательную. Следующую точку 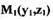 берут
берут
на касательной вблизи точки 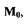 находят
находят 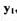 ,
, 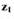 и определяют направление
и определяют направление
касательной 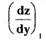 по формуле (1.3) и так далее. Огибающая вдоль
по формуле (1.3) и так далее. Огибающая вдоль
касательных прямых будет фазовой траекторией системы.
- 11 -
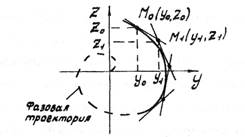
Рис. 1.4. Иллюстрация к построению фазовой траектории САР
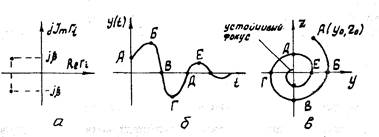
Рис. 1.5. Распределение корней характеристического уравнения (а), свободное движение (б) и фазовая траектория (в) устойчивой САР второго порядка

Рис. 1.6. Распределение корней характеристического уравнения (а), свободное движение (б) и фазовая траектория (в) неустойчивой САР второго порядка
- 12-
Пусть характеристическое уравнение САР имеет комплексно-сопряженные корни с отрицательной вещественной частью (рис.1.5,а). При этом невозмущенное или свободное движение САР происходит по затухающей колебательной кривой (рис. 1.5,6), а фазовая траектория, построенная в плоскости 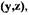 представляет собой сходящуюся к началу координат спираль
представляет собой сходящуюся к началу координат спираль
(рис.1.5,в). Точка А характеризует начальные условия, т.е. в начальный момент система была отклонена на величину 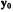 и имела положительную скорость
и имела положительную скорость 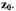 С течением времени выходная координата и скорость уменьшаются до нуля. Начало координат фазовой плоскости такой системы называют устойчивым фокусом.
С течением времени выходная координата и скорость уменьшаются до нуля. Начало координат фазовой плоскости такой системы называют устойчивым фокусом.
Для неустойчивой системы корни характеристического уравнения имеют положительную вещественную часть (рис.1.6,а). В этом случае переходный процесс представляет собой колебательную расходящуюся кривую (рис. 1.6,6), а фазовая траектория - расходящуюся спираль (рис. 1.6,в). Начало координат фазовой плоскости такой системы соответствует положению неустойчивого равновесия и называется неустойчивым фокусом.
Рассмотрим консервативную систему (без потерь энергии). Уравнение свободного движения консервативной системы имеет вид
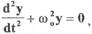 (1.4)
(1.4)
где 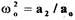 - собственная частота колебаний. Решением уравнения (1.4)
- собственная частота колебаний. Решением уравнения (1.4)
является
 (1.5)
(1.5)
Скорость изменения выходного параметра  будет равна
будет равна
- 13-
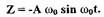 (1.6)
(1.6)
Преобразуя равенства (1.5), (1.6) к виду 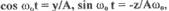 и,
и,
возводя в квадрат последние выражения и складывая их, получим
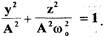 (1.7)
(1.7)
Уравнение (1.7) является уравнением эллипса с полуосями А и 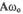 Следовательно, фазовая траектория консервативной системы представляет собой эллипс.Следует отметить, что любой периодический процесс на фазовой плоскости САР изобразится в виде замкнутого контура - замкнутой фазовой траектории. В нелинейных системах с автоколебаниями замкнутые фазовые траектории отделяют область одних типов колебаний от других и их называют предельными циклами. Условием существования автоколебаний в нелинейных системах является баланс притока энергии в систему от внешнего источника и потерь энергии в системе за период колебаний. Такой баланс энергии может наступить только при определенных значениях амплитуды колебаний. Если приток энергии
Следовательно, фазовая траектория консервативной системы представляет собой эллипс.Следует отметить, что любой периодический процесс на фазовой плоскости САР изобразится в виде замкнутого контура - замкнутой фазовой траектории. В нелинейных системах с автоколебаниями замкнутые фазовые траектории отделяют область одних типов колебаний от других и их называют предельными циклами. Условием существования автоколебаний в нелинейных системах является баланс притока энергии в систему от внешнего источника и потерь энергии в системе за период колебаний. Такой баланс энергии может наступить только при определенных значениях амплитуды колебаний. Если приток энергии 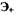 в систему больше, чем потери энергии Э. в ней при любых сколь угодно малых амплитудах возбуждения А, то колебания в САР будут само возбуждающимися и такую систему называют системой с мягким режимом возбуждения автоколебаний (рис. 1.7). Может случиться так, что при амплитудах колебаний
в систему больше, чем потери энергии Э. в ней при любых сколь угодно малых амплитудах возбуждения А, то колебания в САР будут само возбуждающимися и такую систему называют системой с мягким режимом возбуждения автоколебаний (рис. 1.7). Может случиться так, что при амплитудах колебаний 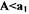 потери энергии
потери энергии 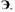 в системе больше притока Энергии
в системе больше притока Энергии  а при -
а при - 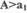 наоборот. Тогда автоколебания будут возникать только при воздействии на систему возмущений с амплитудой большей a1 Следовательно, при
наоборот. Тогда автоколебания будут возникать только при воздействии на систему возмущений с амплитудой большей a1 Следовательно, при 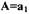 автоколебания неустойчивы, т.к. малейшее отклонение от этого значения амплитуды приводит либо к затуханию колебаний из-за больших потерь энергии, либо к увеличению ампли
автоколебания неустойчивы, т.к. малейшее отклонение от этого значения амплитуды приводит либо к затуханию колебаний из-за больших потерь энергии, либо к увеличению ампли

Рис. 1.7.Иллюстрация к анализу возникновения автоколебаний в САР с мягким режимом возбуждения
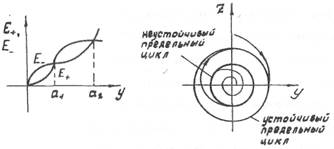
Рис.1.8.Иллюстрация к анализу возникновения автоколебаний в САР с жестким режимом возбуждения
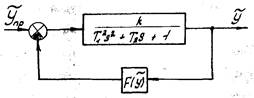
Рис. 1.9. Структурная схема нелинейной САР
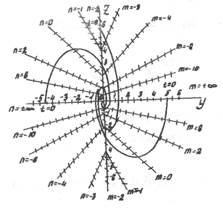
Рис. 1.10. Фазовый потрет нелинейной САР, представленный на рис. 1.9
-16-
колебаний до значения 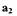 из-за большего притока энергии (рис. 1.8). Такую нелинейную САР называют системой с жестким режимом возбуждения автоколебаний, а предельные циклы с амплитудой а, - неустойчивым предельным циклом, а с амплитудой
из-за большего притока энергии (рис. 1.8). Такую нелинейную САР называют системой с жестким режимом возбуждения автоколебаний, а предельные циклы с амплитудой а, - неустойчивым предельным циклом, а с амплитудой 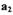 - устойчивым предельным циклом.
- устойчивым предельным циклом.
Рассмотрим построение фазового портрета нелинейной САР, представленной на рис. 1.9. Исходные данные: 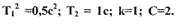 Определим вначале передаточную функцию замкнутой-САР
Определим вначале передаточную функцию замкнутой-САР
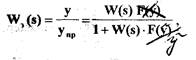 (1.8)
(1.8)
где 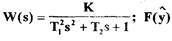 - нелинейная функция. В результате
- нелинейная функция. В результате
преобразования (1.8) с учетом выражения для 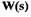 получим
получим
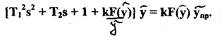
Так как при исследовании устойчивости САР анализируется ее свободное движение, то рассматривается однородное уравнение (без правой части), то есть:
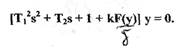
Переходя в последнем уравнении от операторной формы к дифференциальной форме, получим
или 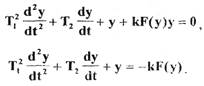 (1.9)
(1.9)
- 17-
Учитывая то, что 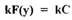 при
при 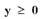 и
и 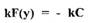 при
при 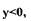
перепишем уравнение (1.9) в виде
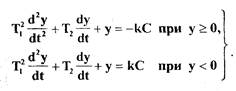 (1.10)
(1.10)
В (1.10) выполним замену 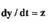 и решим ее относительно
и решим ее относительно 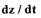
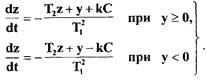 (1.11)
(1.11)
Для исключения 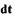 поделим левые и правые части уравнения (1.11) соответственно на левую и правую части
поделим левые и правые части уравнения (1.11) соответственно на левую и правую части 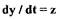
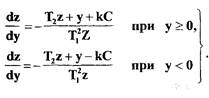 (1.12)
(1.12)
В первом уравнении системы (1.12) обозначим 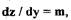 а во втором -
а во втором -
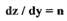 и представим (1.12) в виде
и представим (1.12) в виде
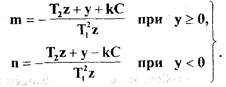 (1.13)
(1.13)
Преобразуем (1.13) с учетом численных значений коэффициентов к виду, удобному для построения фазовой траектории системы
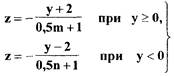 (1.14)
(1.14)
По уравнениям (1.14) для различных значений тип можно построить поле изоклин (рис. 1.10). Наклон фазовой траектории к оси абсцисс для каждой изоклины на рис. 1.10 показан отрезками прямых под углом 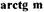 и
и 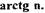
Эти отрезки являются касательными к фазовой траектории . Соединив плавной кривой касательное, получим ряд фазовых траекторий, которые составляют фазовый портрет нелинейной САР. Из анализа фазового портрета следует, что САР устойчива и в ней отсутствует режим автоколебаний.
1.2.2. Метод гармонической линеаризации
Метод гармонической линеаризации или гармонического баланса целесообразно применять при исследовании устойчивости и автоколебаний нелинейных САР, описываемых дифференциальными уравнениями высокого порядка. Достаточно хорошо разработан данный метод для систем, содержащих один существенно нелинейный элемент. Для САР с несколькими нелинейностями метод гармонической линеаризации также может быть использован, но при этом усложняется процедура расчета.
Пусть исследуемая САР содержит один нелинейный элемент, который может быть выделен в структурной схеме в явном виде (рис. 1.11). Условием для применения метода гармонической линеаризации является то, что линейная часть САР должна обладать свойством низкочастотного фильтра, т.е.
- 19-
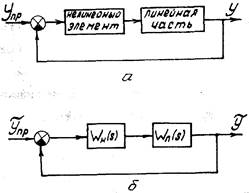
Рис. 1.11. Функциональная (а) и структурная (б) схемы нелинейной САР

Рис. 1.12. Иллюстрация прохождения гармонических колебаний через релейный нелинейный элемент
хорошо пропускать низкочастотные колебания и не пропускать высшие гармоники.
-20-
Предположим, что в нелинейной системе 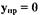 и в ней наблюдается режим
и в ней наблюдается режим
автоколебаний. При этом выходной сигнал, проходя по цепи обратной связи и нелинейный элемент системы, поступает на вход в ее линейную часть. При соблюдении условия низкочастотного фильтра для линейной части системы на выходе из нее будут наблюдаться колебания, близкие по форме к гармоническим Тогда на входе в нелинейное звено сигнал будет также гармоническим:
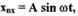 (1.15)
(1.15)
где А, 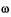 - амплитуда и частота колебаний сигнала на входе в нелинейный элемент. Для релейного нелинейного элемента с характеристикой
- амплитуда и частота колебаний сигнала на входе в нелинейный элемент. Для релейного нелинейного элемента с характеристикой
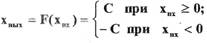 (1.16)
(1.16)
на выходе будут наблюдаться прямоугольные периодические колебаний  (рис. 1.12). При расчете автоколебаний в САР вместо нелинейной функции
(рис. 1.12). При расчете автоколебаний в САР вместо нелинейной функции 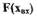 используется гармонически линеаризованная функция
используется гармонически линеаризованная функция
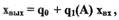 (1.17)
(1.17)
где 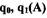 - коэффициенты, учитывающие постоянную составляющую и первую
- коэффициенты, учитывающие постоянную составляющую и первую
гармонику разложения 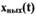 в ряд Фурье. Раскладывая
в ряд Фурье. Раскладывая 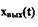 в ряд
в ряд
Фурье, будем иметь
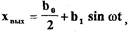 (1.18)
(1.18)
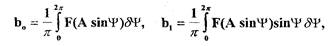
где 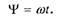
-21-
Для рассматриваемого релейного элемента(см. формулы (1.15), (1.16)) получим

Определим из (1.15) 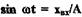 и подставим его в равенство (1.18) с
и подставим его в равенство (1.18) с
учетом того, что 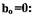
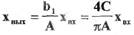
или
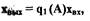 (1.19)
(1.19)
здесь 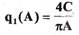 (1.20)
(1.20)
- коэффициент гармонической линеаризации. Формулы для расчета qi(A) для других нелинейных элементов приведены в прил. 1,
Если характеристика нелинейного элемента неоднозначная, например, с гистерезисными петлями или зависит как от входной величины, так и от ее
скорости 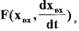 то линеаризованная зависимость определяется по
то линеаризованная зависимость определяется по
формуле
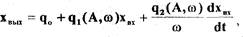 (1.21)
(1.21)
- 22 -где 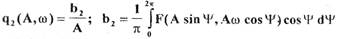
qo, qi определяются по выражениям, аналогичным релейному элементу. Нелинейные свойства САР учтены в коэффициентах 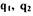 тем, что они в
тем, что они в
общем случае зависят от амплитуды и частоты входного сигнала .
При исследовании автоколебаний САР методом гармонической линеаризации используется передаточная функция нелинейного элемента (см. формулу (1.21))
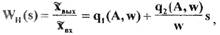 (1.22)
(1.22)
где 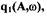
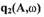 - коэффициенты гармонической линеаризации,
- коэффициенты гармонической линеаризации,
Передаточная функция замкнутой САР (см.рис.1.11) определяется выражением
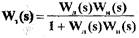 (1.23)
(1.23)
Предположим, что САР в разомкнутом состоянии устойчива. Тогда на основании критерия Найквиста она в замкнутом состоянии находится на границе устойчивости, если частотная функция разомкнутой системы 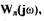
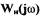 проходит через точки с координатой
проходит через точки с координатой 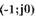 или
или
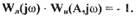 (1.24)
(1.24)

Рис. 1.13. Иллюстрация к определению частоты и амплитуды возможных автоколебаний в нелинейной САР
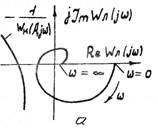
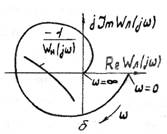
Рис. 1.14. Иллюстрация к анализу устойчивости нелинейной САР

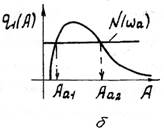
Рис. 1.15. Гармоническое определение амплитуды возможных автоколебаний в нелинейной САР с релейным нелинейным элементом (а) и нелинейным релейным элементом с люфтом ( if)
-24-
При этом в системе могут наблюдаться колебания, которые в случае их устойчивости будут автоколебаниями. Определение амплитуды и частоты автоколебаний в нелинейной системе на основании равенства (1.24) может быть выполнено графически и алгебраически. Рассмотрим первый из этих методов, который называют еще методом Гольдфарба. Преобразуем (1.24) к следующему виду
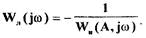 (1.25)
(1.25)
Из (1.25) следует, что если характеристики  и
и 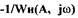 пересекаются, то в точке их пересечения по
пересекаются, то в точке их пересечения по 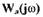 можно определить частоту
можно определить частоту 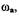 а по
а по 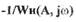 - амплитуду
- амплитуду 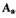 .Устойчивость автоколебаний, т.е. факт
.Устойчивость автоколебаний, т.е. факт
их существования, проверяют в результате анализа поведения САР при малых изменениях амплитуды 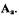 Если при увеличении
Если при увеличении 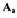 на
на 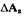 колебания
колебания
затухают, а при уменьшении на 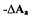 - расходятся, то найденный режим является режимом устойчивых автоколебаний, в противном случае автоколебания в САР отсутствуют. Такой анализ можно провести с использованием критерия Найквиста. Колебания с амплитудой
- расходятся, то найденный режим является режимом устойчивых автоколебаний, в противном случае автоколебания в САР отсутствуют. Такой анализ можно провести с использованием критерия Найквиста. Колебания с амплитудой 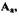 частотой
частотой 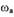 будут автоколебаниями, если \¥л0(») не охватывает точку на характеристике -
будут автоколебаниями, если \¥л0(») не охватывает точку на характеристике - 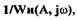 полученной увеличением
полученной увеличением 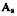 на величину
на величину 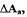 и охватывает точку этой характеристики, полученной уменьшением
и охватывает точку этой характеристики, полученной уменьшением 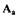 на
на 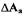 (рис.1.13). . В САР возникают автоколебания, если характеристика
(рис.1.13). . В САР возникают автоколебания, если характеристика 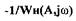 будет расположена вне
будет расположена вне 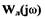 (рис.1.14,а). Если
(рис.1.14,а). Если 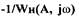 размещена внутри области, охваченной
размещена внутри области, охваченной 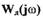 (рис.1.14,6), то колебания будут расходящимися, т.е. САР неустойчива в том смысле, как неустойчива линейная САР. Алгебраический способ определения
(рис.1.14,6), то колебания будут расходящимися, т.е. САР неустойчива в том смысле, как неустойчива линейная САР. Алгебраический способ определения 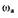 и
и 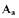 основан на анализе собственного оператора замкнутой САР. Предположим, что характеристика нелинейного элемента нечетная, однозначная и его пер-ная ф-ция
основан на анализе собственного оператора замкнутой САР. Предположим, что характеристика нелинейного элемента нечетная, однозначная и его пер-ная ф-ция
25- равна
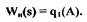 (1.26)
(1.26)
Предположим также, что передаточная функция устойчивой линейной части имеет вид
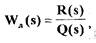 (1.27)
(1.27)
тогда на основании равенства (1.23) с учетом (1.27) передаточная функция замкнутой САР определяется выражением
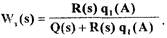 (1.28)
(1.28)
Из теории устойчивости известно, что незатухающие колебания в системе с постоянными коэффициентами могут иметь место при наличии чисто мнимых корней характеристического полинома 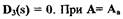 из (1.28)
из (1.28)
следует
 (1.29)
(1.29)
где 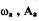 - частота и амплитуда возможных автоколебаний. Для определения
- частота и амплитуда возможных автоколебаний. Для определения
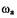 и
и 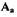 в последнем уравнении выделяем вещественную и мнимую части и
в последнем уравнении выделяем вещественную и мнимую части и
приравниваем их к нулю
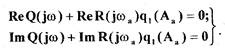 (130)
(130)
Исключая из этих уравнений 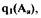 получим
получим
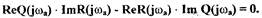 (1.31)
(1.31)
-26-
Вещественные корни уравнения (1.31) являются возможными частотами автоколебаний. Отсутствие вещественных корней будет указывать на то, что автоколебаний в системе нет. Пусть 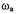 является вещественным корнем, тогда, подставляя его в любое из уравнений (1.30), находим
является вещественным корнем, тогда, подставляя его в любое из уравнений (1.30), находим 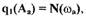
где 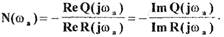 (1.32)
(1.32)
Амплитуду возможных автоколебаний можно определить и аналитически, если, например, нелинейный элемент имеет релейную характеристику (см.рис. 1.1,а) и его коэффициент гармонической линеаризации вычисляется по формуле (1.20). В этом случае амплитуда автоколебанийна ходится из выражения
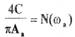
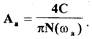 (1.33) При графическом определении
(1.33) При графическом определении 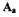 на график гармонически
на график гармонически
линеаризованной нелинейной функции наносится зависимость 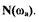 Так как
Так как
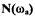 не зависит от
не зависит от 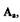 то на графике (рис. 1.15,а)
то на графике (рис. 1.15,а) 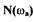 проходит параллельно
проходит параллельно
оси абсцисс. В случае параллельной релейной характеристики всегда будут существовать точки пересечения кривой 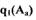 с
с  то есть будут возможны
то есть будут возможны
автоколебания (см.рис. 1.14,а). Однако с ростом 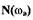 значения
значения  снижаются
снижаются
и в пределе будет режим с бесконечно малой частотой колебаний. Если релейная характеристика будет с "люфтом" (см.рис. 1.1,б), то функции для определения амплитуд автоколебаний пройдут так, как показано на рис. 1.15,6. В этом случае прямая 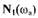 пересекает характеристику
пересекает характеристику 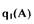 в
в
двух точках. Для выявления того, какая из этих точек пересечения будет
-27-

Рис. 1.16 Годограф Михайлова замкнутой нелинейной
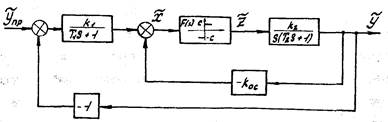
Рис.1.17. Структурная схема САР с релейным
нелинейным элементом
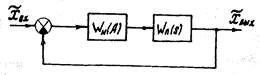
Рис. 1.18. Преобразованная структурная схема нелинейной САР
соответствовать устойчивым автоколебаниям в САР, необходимы дополнительные исследования.Устойчивость режима автоколебаний можно проверить по критерию Михайлова, исследовав годограф (см. формулу (1.29)) замкнутой САР
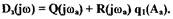 (1.34)
(1.34)
Равенство 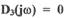 соответствует прохождению годографа Михайлова
соответствует прохождению годографа Михайлова
через начало координат при частоте 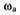 и амплитуде возможных
и амплитуде возможных 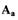
автоколебаний. Дадим малое приращение 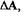 т.е.
т.е. 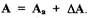 Вследствие
Вследствие
изменения 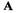 изменяется
изменяется  и соответственно отклоняется кривая
и соответственно отклоняется кривая
Михайлова в ту или иную сторону.В том случае,когда годограф Михайлова займет положение 1(рис. 1.1.6),колебания в САР будут затухать,а в положении 2 -возрастать.Следовательно,для устойчивости режима автоколебаний необходимо,чтобы при 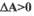 критерий Михайлова удовлетворялся, а при
критерий Михайлова удовлетворялся, а при 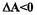 - неудовлетворялся.Аналитически данное условие можно сформулировать в виде неравенства,полученного из анализа деформации годографа Михайлова при малых изменениях частоты и амплитуды возможных автоколебаний.Для того,чтобы режим автоколебаний был устойчивым,необходимо и достаточно, чтобы при
- неудовлетворялся.Аналитически данное условие можно сформулировать в виде неравенства,полученного из анализа деформации годографа Михайлова при малых изменениях частоты и амплитуды возможных автоколебаний.Для того,чтобы режим автоколебаний был устойчивым,необходимо и достаточно, чтобы при 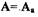 и
и 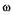
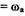 выполнялось неравенство
выполнялось неравенство
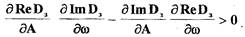 (1.35)
(1.35)
Этого условия достаточно для систем с линейной частью, имеющей порядок характеристического уравнения 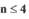 . Для систем с
. Для систем с 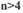 необходимо, чтобы при значении
необходимо, чтобы при значении 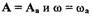 характеристика
характеристика 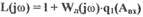
проходила через начало координат, а в остальном удовлетворяла критерию устойчивости Михайлова.
Рассмотрим применение метода гармонической линеаризации для анализа возможных автоколебаний в нелинейной САР, структурная схема которой представлена на рис. 1.17. Нелинейный элемент имеет однозначную релейную характеристику, коэффициент гармонической линеаризации которого был определен ранее (см. формулу (120)).
Структурную схему на рис. 1.17 можно преобразовать к виду, удобному для применения метода гармонической линеаризации, т.е. выделив линейный блок и нелинейный элемент (рис.1.18). Передаточная функция линейной части САР определяется при предположении , что входным ее параметром является выходной сигнал 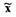 нелинейного элемента, а выходным - входной параметр z нелинейного элемента, а
нелинейного элемента, а выходным - входной параметр z нелинейного элемента, а 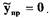 Тогда на основании преобразования
Тогда на основании преобразования
структурной схемы линейной части САР (рис. 1.19) можно определить ее передаточную функцию
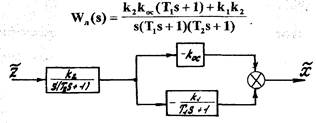 (1.36)
(1.36)
Рис Л. 19. Структурная схема линейной части САР
Учитывая, что для релейного нелинейного элемента  определим по формуле (1.23) с учетом (1.36) передаточную функцию замкнутой САР
определим по формуле (1.23) с учетом (1.36) передаточную функцию замкнутой САР
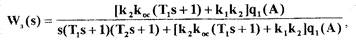
знаменатель которой представляет собой собственный оператор системы
-30-
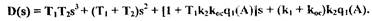
Определим амплитуду 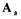 и частоту
и частоту 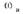 возможных автоколебаний
возможных автоколебаний
алгебраическим способом. Для этого подставим в собственный оператор  и выделим действительную и мнимую части
и выделим действительную и мнимую части
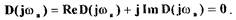
Здесь
 (1.37)
(1.37)
Из первого уравнения (1.37) определим выражение для коэффициента линеаризации
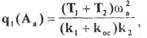 (1.38)
(1.38)
подставив которое во второе уравнение, находим частоту возможных автоколебаний
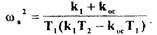 (1.39)
(1.39)
Имея в виду , что для релейного элемента  определим из
определим из
(1.38) и (1.39) выражение для расчета амплитуды возможных автоколебаний
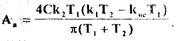 (1.40)
(1.40)
-31 –
Для проверки устойчивости режима автоколебаний воспользуемся формулой (1.35). Для этого определим частные производные:
 (1.41)
(1.41)
Подставляя частные производные (1.41) в неравенство (1.35), получим
 (1.42)
(1.42)
Следовательно, для реализации режима автоколебаний в нелинейной САР необходимо, чтобы выполнялось неравенство (I. .42).
-32-
1.2.3.Теорема Ляпунова об устойчивости САР
При проектировании САР важно знать, как поведет себя реальная САР, находящаяся на границе устойчивости, рассчитанной по параметрам, определенным по линеаризованной модели (методом малых отклонений). Этого нельзя сказать без дополнительных исследований. Кроме того, проектировщиков САР часто интересует вопрос: будет ли нелинейная система устойчива в принципе, какие соотношения должны существовать для этого между характеристиками линейной части и нелинейного элемента. Ответ на эти вопросы может быть получен, если воспользоваться прямым методом Ляпунова, называемым иногда второй метод Ляпунова. Рассмотрим сущность этого метода.
Предположим, что САР описывают системой уравнений 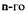 порядка,
порядка,
которую можно записать в следующей нормальной форме Коши;
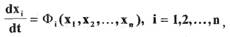
где 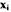 - координаты состояния системы. Функции удовлетворяют условию
- координаты состояния системы. Функции удовлетворяют условию 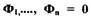 при
при 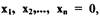 т.к. в установившемся состоянии все
т.к. в установившемся состоянии все
отклонения переменных и их производные равны нулю.
Если 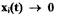 при
при 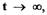 то невозмущенное движение называется
то невозмущенное движение называется
асимптотически устойчивым. Если  при
при 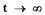 после любых
после любых
начальных отклонений, то система называется устойчивой в целом. Существует еще понятие абсолютной устойчивости, означающее асимптотическую устойчивость системы в целом при любом характере нелинейности внутри определенного класса нелинейностей, например, внутри определенного сектора в плоскости характеристики нелинейного элемента.
В общем случае в нелинейных системах, в отличие от линейных, устойчивость состояния равновесия не означает, что будут устойчивы
-33-
процессы во всем диапазоне режимов работы, т.к. свойства нелинейной системы меняются с изменением координат состояния. Например, в некоторых системах нелинейная САР устойчива в окрестности начала координат и неустойчива при превышении определенного значения параметра возмущения, т.е. система устойчива в малом и неустойчива в большом.
В дальнейшем нам придется иметь дело с непрерывными функциями координат состояния системы  обладающими свойством
обладающими свойством 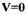 при
при
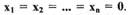 Такая функция называется знакоопределенной, если во всей рассматриваемой области, содержащей начало координат, она сохраняет один и тот же знак и обращается в нуль только в начале координат. Например, при
Такая функция называется знакоопределенной, если во всей рассматриваемой области, содержащей начало координат, она сохраняет один и тот же знак и обращается в нуль только в начале координат. Например, при 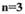 может быть такая знакоопределенная функция
может быть такая знакоопределенная функция
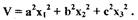
Знакоопределешшя функция может быть положительно определенной или отрицательно определенной. Если же функция 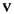 обращается в нуль не только в начале координат, то такая функция называется знакопостоянной (положительной или отрицательной). Например, при
обращается в нуль не только в начале координат, то такая функция называется знакопостоянной (положительной или отрицательной). Например, при 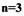 функция
функция
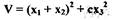
обращается в нуль на прямой 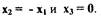
Наконец, функцию 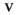 называют знакопеременной, если она в
называют знакопеременной, если она в
рассматриваемой области не сохраняет одного и того же знака, например
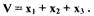
Функции 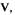 обращающиеся в нуль в начале координат, играют важную роль в теоремах Ляпунова об устойчивости и неустойчивости нелинейных систем и они называются функциями Ляпунова.
обращающиеся в нуль в начале координат, играют важную роль в теоремах Ляпунова об устойчивости и неустойчивости нелинейных систем и они называются функциями Ляпунова.
-34-
Производная от функции Ляпунова по времени будет равна
:
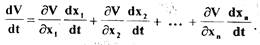 (1.43)
(1.43)
Подставляя вместо  правые части уравнений САР в форме Коши, т.е.
правые части уравнений САР в форме Коши, т.е.
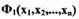 , получим производную от функции Ляпунова по времени в виде
, получим производную от функции Ляпунова по времени в виде
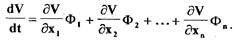 (1.44)
(1.44)
Следовательно, 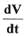 так же, как и сама функция
так же, как и сама функция 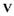 Ляпунова, является
Ляпунова, является
некоторой функцией координат, т.е:
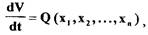
причем это выражение так же, как и сама функция 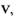 тождественно обращается в нуль при
тождественно обращается в нуль при  Поэтому к
Поэтому к 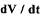 можно применять такие же
можно применять такие же
понятия, как знакоопределенность, знакопостоянство и знакопеременность в некоторой области вокруг начала координат, как и для функции 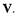
Теорема Ляпунова об устойчивости систем. Если для САР с дифференциальным уравнением 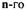 порядка можно подобрать такую
порядка можно подобрать такую
знакоопределенную функцию Ляпунова 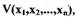 что ее производная по
что ее производная по
времени  ТОЖе будет знакоопределенной (или
ТОЖе будет знакоопределенной (или
знакопеременной), но имеет знак, противоположный знаку 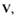 то данная
то данная
система устойчива. При знакоопределенной функции 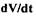 будет наблюдаться
будет наблюдаться
асимптотическая устойчивость нелинейной САР.
-35-
Эта теорема Ляпунова дает достаточные условия устойчивости нелинейной системы, которые не всегда будут и необходимыми. При выполнении условий теоремы Ляпунова система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы по параметрам. В самом деле, если выбрана функция 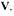 удовлетворяющая теореме Ляпунова, то нет уверенности в том, что нельзя подобрать другой вариант функции
удовлетворяющая теореме Ляпунова, то нет уверенности в том, что нельзя подобрать другой вариант функции 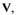 который бы еще более полно охватывал область устойчивости данной системы. Так как сформулированная теорема Ляпунова дает достаточные условия устойчивости, вообще говоря, не охватывающие всю область устойчивости системы, то могут представить интерес условия, при которых САР наверняка становится неустойчивой.
который бы еще более полно охватывал область устойчивости данной системы. Так как сформулированная теорема Ляпунова дает достаточные условия устойчивости, вообще говоря, не охватывающие всю область устойчивости системы, то могут представить интерес условия, при которых САР наверняка становится неустойчивой.
Теорема Ляпунова о неустойчивости систем. Если при заданных в форме Коши уравнениях САР п-го порядка производная 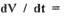
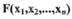 окажется знакоопределенной, причем сама функция V в какой-нибудь области , прилегающей к началу координат, будет иметь знак, одинаковый со знаком производной
окажется знакоопределенной, причем сама функция V в какой-нибудь области , прилегающей к началу координат, будет иметь знак, одинаковый со знаком производной  то данная система неустойчива.
то данная система неустойчива.
Теоремы Ляпунова сыграли большую роль в инженерной практике, когда не были еще созданы другие методы исследования нелинейных САР. Они использовались, как правило, для анализа устойчивости систем с невысоким порядком характеристического уравнения.
Рассмотрим пример исследования устойчивости системы управления курсом самолета методом Ляпунова. Для этого запишем уравнения САУ в упрощенной постановке.
Уравнение движения самолета в горизонтальной плоскости имеет вид
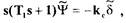 (1/45)
(1/45)
где 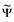 - угол поворота самолета;
- угол поворота самолета; 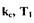 - коэффициент передачи и постоянная
- коэффициент передачи и постоянная
времени самолета; 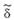 - угол поворота руля самолета.
- угол поворота руля самолета.
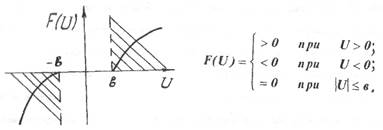 Рис. 1.20. Статическая характеристика рулевого привода
Рис. 1.20. Статическая характеристика рулевого привода 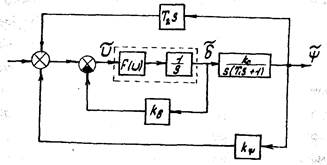
Рис. 1.21. Структурная схема САУ курса самолета
Привод руля самолета описывается зависимостью
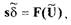 (1.46)
(1.46)
где  - нелинейная функция, описывающая статическую характеристику
- нелинейная функция, описывающая статическую характеристику
рулевого привода; 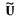 - напряжение на входе в усилитель рулевого привода.
- напряжение на входе в усилитель рулевого привода.
Предположим, что нелинейная функция 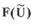 представляет собой в общем
представляет собой в общем
случае произвольную кривую (рис. 1.20).
Измерительное устройство с обратными связями описывается уравнением
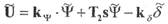 (1.47)
(1.47)
Структурная схема, соответствующая приведенным уравнениям, представлена на рис. 1.21. Для исследования устойчивости САУ по методу Ляпунова приведем уравнения (1.45) - (1.47) к канонической форме. Для этого представим уравнение (1.45) в виде
 (1.48)
(1.48)
Введем обозначения:
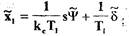 (1.49)
(1.49)
 (1.50)
(1.50) 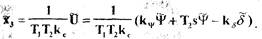 (1.51)
(1.51)
-38-
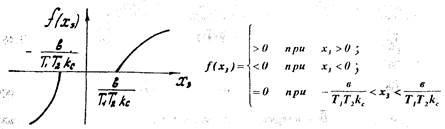
Рис.1.22. Статическая характеристика рулевого привода самолета
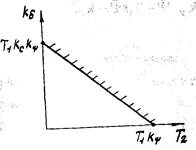
Рис 1.23. Область абсолютной устойчивости САР в плоскости параметров 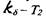
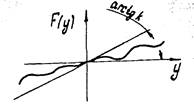
Рис. 1.24. Статическая характеристика нелинейного элемента
-39-
С учетом введенных обозначений статическую характеристику рулевого привода можно преобразовать к виду, представленному на рис. 1.22.
Предположим, что оператор Лапласа s играет здесь только роль операции дифференцирования 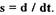 Опуская волнистые черточки над параметрами,
Опуская волнистые черточки над параметрами,
определим производные по времени от 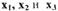 (см. формулы (1.49) - < 1.51)):
(см. формулы (1.49) - < 1.51)):
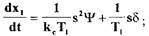 (1.52)
(1.52) 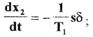 (1.53)
(1.53)
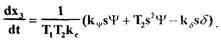 (1.54)
(1.54)
Попытаемся освободиться в уравнении (1.52) от переменных 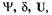 выразив их через новые переменные
выразив их через новые переменные 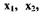 и
и 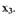 Для этого преобразуем
Для этого преобразуем
уравнение (1.52) с учетом того, что
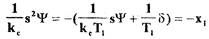
(см. уравнения (1.48), (1.49)); 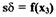 (см. уравнение (1.46)), и статическую
(см. уравнение (1.46)), и статическую
характеристику рулевого привода на рис. 1.22 к виду
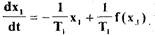 (1.55)
(1.55)
Введем безразмерное время 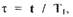 тогда
тогда 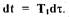 Приведем
Приведем
уравнение (1.55) к следующей форме с учетом того, что 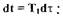
-40-
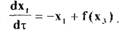 (1.56)
(1.56)
Аналогично можно преобразовать уравнение (1.53)
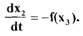 (I.57)
(I.57)
Уравнение (1.54) перепишем в следующем виде ;
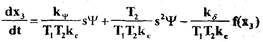 .(1.58)
.(1.58)
s
Так как 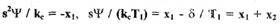 (см. уравнения
(см. уравнения
(1.48), (1.50)), то уравнение (1.58) представим в виде:
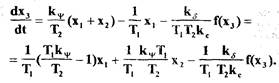 (1.59) Выразив уравнение (1.59) через безразмерное время, получим
(1.59) Выразив уравнение (1.59) через безразмерное время, получим
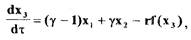 (1.60)
(1.60)
где 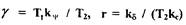 - постоянные, т.к.
- постоянные, т.к. 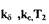 - величины
- величины
постоянные и  то решение уравнений будет зависеть от величины
то решение уравнений будет зависеть от величины 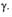 Здесь
Здесь
могут быть два решения: 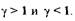
Рассмотрим случай 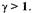 Функцию Ляпунова выберем в виде
Функцию Ляпунова выберем в виде
-41 -
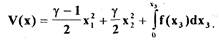 (1.61)
(1.61)
При 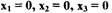 справедливо равенство
справедливо равенство 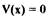 и функция
и функция 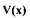
является знакоопределенной, т.к. при всех значениях 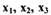 функция
функция 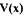
при 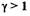 положительна.
положительна.
Производная от функции Ляпунова равна
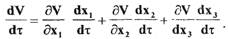 (1.62) Определим частные производные функции Ляпунова по
(1.62) Определим частные производные функции Ляпунова по 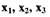
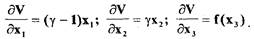 (1.63)
(1.63)
Подставляя полученные выражения (1.63) в (1.62), с учетом (1.56), (1.57), (1.58) получим
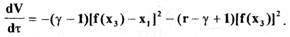
Функция 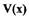 является положительно определенной.Производная
является положительно определенной.Производная 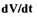
является отрицательной знакопостоянной функцией при условии
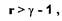 если
если  (1.64)
(1.64)
Следовательно, исследованная САУ при указанных условиях устойчива асимптотически.
-42-
Аналогично можно выбрать функцию Ляпунова для случая 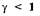 и
и
провести исследование устойчивости САУ для данного случая
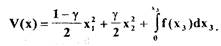 (1.65)
(1.65)
Определив частные производные 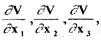 с учетом выражения
с учетом выражения
(1.65) можно получить
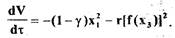 (1.66)
(1.66)
Отсюда условие устойчивости САУ 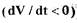 принимает вид:
принимает вид:
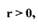 если
если 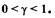 (1-67)
(1-67)
Условия (1.64) и (1.67) устойчивости САУ можно переписать в следующем виде :
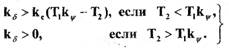 (1.68)
(1.68)
Графически условия (1.68) можно представить так, как показано на рис. 1.23.
Из графика ясно, что при малом коэффициенте 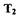 для обеспечения устойчивости САР коэффициент
для обеспечения устойчивости САР коэффициент  местной обратной связи должен быть большим.
местной обратной связи должен быть большим.
-43-
1.2.4. Анализ устойчивости нелинейной САР частотным методом В.М. Попова
Для исследования абсолютной устойчивости систем, содержащих в своей структуре нелинейный элемент с однозначной характеристикой, румынский ученый В.М.Попов предложил частотный критерий, суть которого заключается в проверке определенного условия в плоскости модифицированной частотной характеристики линейной части САР. Пусть передаточная функция линейной части нелинейной САР (см .рис. 1.11) описывается зависимостью
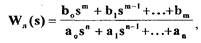 (1.69)
(1.69)
причем m < п и линейная часть системы представляет собой устойчивый блок. Представим себе, что характеристика нелинейного элемента располагается таким образом, что можно провести прямую с углом наклона 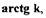 при этом
при этом
вся характеристика нелинейного звена располагается несимметрично по одну сторону от этой прямой (рис. 1.24). Для такой системы критерий устойчивости В.М.Попова (без доказательства) формулируется так. Для абсолютной устойчивости САР с одним однозначным нелинейным звеном и устойчивой линейной частью с частотной функцией 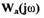 достаточно, чтобы при
достаточно, чтобы при 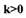
существовало такое вещественное число 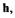 что при всех
что при всех 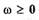 выполнялось
выполнялось
неравенство
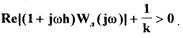 (1.70)
(1.70)
Более наглядна другая, графическая интерпретация частотного критерия В.М.Попова, который рассматривается в плоскости модифицированной частотной характеристики линейной части
-44-
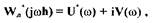 (1-71)
(1-71)
где  - нормирующий множитель,
- нормирующий множитель,
например 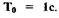 Дтя дальнейшего анализа преобразуем левую часть
Дтя дальнейшего анализа преобразуем левую часть
неравенства(1.70)
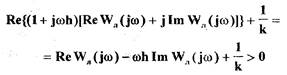
или с учетом (1.71)
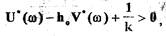 (1.72)
(1.72)
где 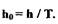
Выражение 
является уравнением прямой в плоскости 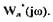 Из (1.72) с учетом
Из (1.72) с учетом
последнего условия следует
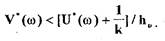 (1.73)
(1.73)
Тогда формулировка критерия В.М.Попова для случая использования модифицированной частотной функции линейной части САР примет такое содержание. Для абсолютной устойчивости нелинейной САР достаточно подобрать такую прямую в плоскости 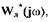 проходящую через точку с
проходящую через точку с
координатой  что вся кривая
что вся кривая 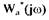 лежит справа от этой прямой,
лежит справа от этой прямой,
(рис. 1.25, 1.26). Критерий устойчивости В.М.Попова выражает как необходимые, так и достаточные условия абсолютной устойчивости нелинейной САР.
-45-
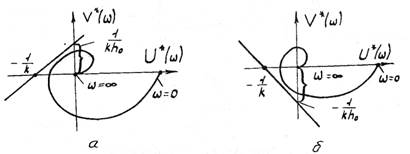
Рис.1.25. Модифицированная частотная характеристика линейной части абсолютно устойчивой нелинейной САР
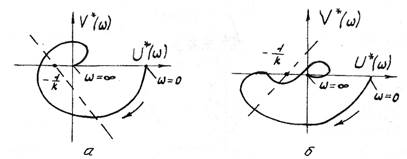
Рис. 1.26. Модифицированная частотная характеристика линейной части абсолютно неустойчивой нелинейной САР
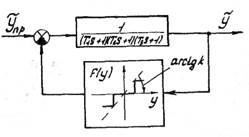
Рис.1.27. Структурная схема линейной САР
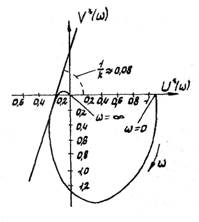
Рис. 1.28. Модифицированная частотная характеристика линейной части абсолютно устойчивой нелинейной САР
В качестве примера рассмотрим анализ устойчивости нелинейной САР, представленной на рис. 1.27.
Коэффициент передачи линейной части САР можно условно отнести к нелинейному звену 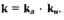 Требуется определить, при каких значениях
Требуется определить, при каких значениях 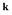
САР абсолютно устойчива, если характеристика нелинейного звена расположена в секторе 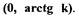 Исходные данные:
Исходные данные: 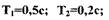
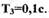 Определим выражение для частотной функции линейной части САР
Определим выражение для частотной функции линейной части САР
где . . 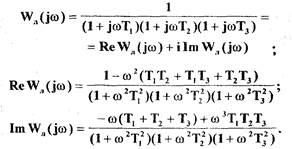
Таким образом может быть определена модифицированная частотная функция (1.71) линейной части САР.
В результате подстановки цифровых значений 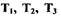 и построения
и построения
получим модифицированную частотную функцию линейной части нелинейной САР, представленную на рис.1.28. Из рис.1.28 следует, что прямая проходит через точку пересечения модифицированной характеристики линейной части САР с осью абсцисс, т.е. соответствует 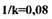 или
или 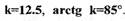
Нелинейная САР абсолютно устойчива для всех нелинейных элементов, характеристики которых лежат в секторе 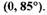
- 48 –
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНОЙ САР ЧАСТОТЫ ВРАЩЕНИЯ ТУРБОПРИВОДА
2.1. Назначение и принцип действия САР
САР предназначена для изменения и поддержания частоты вращения ,турбопривода стационарной промышленной установки (рис.2.1), например, компрессора, насоса и т.д. Гидромеханический регулятор непрямого действия за счет изменения расхода пара, подаваемого на турбину (регулирующего фактора), управляет частотой вращения привода (регулируемым параметром).
Регулятор частоты вращения содержит центробежный чувствительный элемент - импеллер, установленный на одном валу с турбиной, гидроусилитель, состоящий из узла .мембраны и струйного усилителя, исполнительный орган (паровой клапан), приводимый в движение от сервомотора, управляемого струйным усилителем.
При изменении нагрузки регулирование частоты вращения турбопривода происходит следующим образом. Пусть нагрузка на турбину увеличилась, т.е. увеличилась отбираемая агрегатом 2 мощность, что привело к снижению частоты вращения п турбины 1. Одновременно снижается частота вращения чувствительного элемента - импеллера 3, давление масла на выходе из импеллера уменьшается, что вызывает прогиб мембраны 4 вниз. Мембрана через жестко прикрепленный к ней шток приводит в движение сопло 5 струйного усилителя, которое, поворачиваясь относительно шарнира по часовой стрелке, подает масло высокого давления в нижний канал распределителя 7.Равновесие сервомотора 9 при этом нарушается, поршень под действием большего давления в верхней полости смещается вниз, открывая паровой клапан и увеличивая расход пара в турбину. Частота вращения привода восстанавливается до исходного значения, задаваемого натягом пружины 6.
- 49-
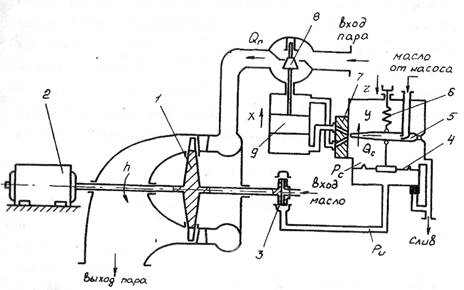 Рис.2.1. Принципиальная схема САР частоты вращения парового турбопривода
Рис.2.1. Принципиальная схема САР частоты вращения парового турбопривода
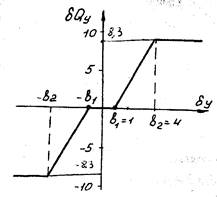 Рис.2.2. Безразмерная расходная характеристика струйного усилителя
Рис.2.2. Безразмерная расходная характеристика струйного усилителя
-50-
Предварительный анализ структуры САР позволил выделить элемент системы, линеаризация характеристики которого методом малых отклонений приводит к существенной погрешности при расчете динамических характеристик САР и поэтому недопустима. Таким нелинейным элементом является струйный гидроусилитель, расходная характеристика которого представлена на рис.2.2. Наличие такого звена может привести к возникновению в САР автоколебаний, параметры которых требуется определить.
2.2. Вывод уравнений звеньев САР
Уравнение звеньев выводится для положительных направлений координат, соответствующих направлению движения элементов САР при увеличении частоты вращения турбопривода. При выводе учитывается ряд допущений исходя из низкочастотной модели элементов регулятора и возможности линеаризации характеристик нелинейных элементов.
Уравнение объекта регулирования Вывод уравнения движения турбопривода производится с учетом следующих допущений:
- параметры рабочего тела (пара) на входе в турбину и выходе из нее неизменны;
- коэффициент полезного действия турбины постоянен;
- влияние объемов по паровому тракту на динамические свойства
турбопривода незначительно;
- изменение параметров установившегося режима является малым.
Исходя из принятых допущений движение.турбопривода описывается
следующим уравнением:
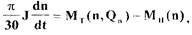 (2.1)
(2.1)
-51 –
где 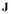 - момент инерции ротора турбины совместно с нагрузкой;
- момент инерции ротора турбины совместно с нагрузкой;  момент, развиваемый турбиной;
момент, развиваемый турбиной; 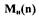 - момент сопротивления нагрузки,
- момент сопротивления нагрузки,
пропорциональный частоте вращения, что справедливо, например, для компрессора, насоса и т.д. Линеаризуем уравнение (2.1) из условия малости отклонений параметров. Разложим нелинейные зависимости 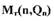 и
и
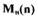 в ряд Тейлора и удержим первые члены ряда:
в ряд Тейлора и удержим первые члены ряда:
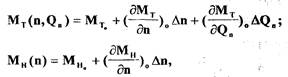
где 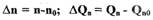 - отклонения частоты вращения и расхода пара
- отклонения частоты вращения и расхода пара
относительно установившихся значений; 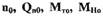 - установившиеся
- установившиеся
значения частоты вращения, расхода пара, моментов турбины и нагрузки
соответственно; 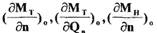 - частные производные
- частные производные
моментных характеристик, определенные в точке, соответствующей установившемуся режиму.
Переходя от уравнения (2.1) к уравнению относительно отклонений параметров и учитывая, что на установившемся режиме 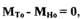 получим
получим
следующее равенство:
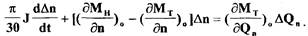 (2.2)
(2.2)
Вводим безразмерные параметры 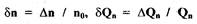 и
и
перепишем уравнение (2.2) в виде:
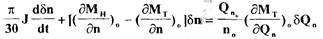 (2.3)
(2.3)
или в стандартной форме
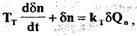 (2.4)
(2.4)
где 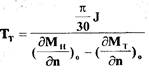 - постоянная времени турбопривода;
- постоянная времени турбопривода;
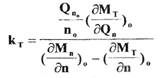 - коэффициент усиления турбопривода по расходу пара.
- коэффициент усиления турбопривода по расходу пара.
Уравнение чувствительного элемента (импеллера) Чувствительный элемент системы представляет собой импеллер -малогабаритный центробежный насос, преобразующий частоту вращения 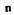 в давление рабочей жидкости (масла) на выходе
в давление рабочей жидкости (масла) на выходе 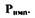 Статическая
Статическая
характеристика импеллера может быть аппроксимирована зависимостью:
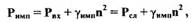
где  - давление рабочей жидкости на входе в импеллер, в нашем случае
- давление рабочей жидкости на входе в импеллер, в нашем случае
оно равно давлению в сливной магистрали; 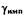 - постоянный коэффициент.
- постоянный коэффициент.
Рассматривая малые отклонения параметров относительно установившихся значений  и учитывая, что
и учитывая, что  (изменением
(изменением
давления в сливной магистрали можно пренебречь), можно записать:
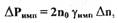
где коэффициент 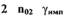 представляет собой тангенс угла наклона
представляет собой тангенс угла наклона
касательной к статической характеристике импеллера  в точке
в точке
установившегося режима.
- 53 –
Переходя в последнем уравнении к безразмерным параметрам, получаем уравнение чувствительного элемента:
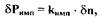 (2.5)
(2.5)
где 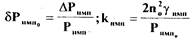 - коэффициент усиления импеллера.
- коэффициент усиления импеллера.
Уравнение движения трубки струйного усилителя.
В рассматриваемой САР применен усилитель с качающейся струйной трубкой 5 ( см.рис.2.1) , соединенной шарнирами со штоком мембраны 4 и' пружиной 6. На мембрану действует перепад давления на выходе из импеллера 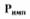 и слива
и слива 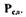 Регулировочная пружина 6 предназначена для настройки
Регулировочная пружина 6 предназначена для настройки
требуемого значения частоты вращения привода (за счет регулировки натяга изменением координаты заделки пружины г) . Для повышения устойчивости САР в магистрали подвода масла от импеллера к мембране установлен демпфирующий жиклер с площадью проходного сечения 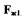 , а нижняя
, а нижняя
полость мембраны соединена со сливом через сливной жиклер с площадью проходного сечения 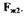 Запишем уравнение баланса расходов для полости под
Запишем уравнение баланса расходов для полости под
мембраной
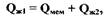 (2.6)
(2.6)
где 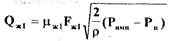 - расход жидкости через демпфирующий
- расход жидкости через демпфирующий
жиклер; 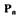 - давление в полости под . мембраной;
- давление в полости под . мембраной;
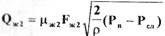 - расход жидкости через сливной жиклер;
- расход жидкости через сливной жиклер;  плотность жидкости;
плотность жидкости; 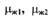 - коэффициенты расходов демпфирующего и
- коэффициенты расходов демпфирующего и
сливного жиклеров соответственно; 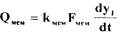 - расход масла,
- расход масла,
-54-
обусловленный перемещением мембраны; 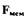 - площадь мембраны,
- площадь мембраны, 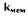
коэффициент, учитывающий форму прогиба мембраны.
Перепишем уравнение (2.6) в малых отклонениях параметров от установившихся значений
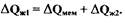 (2.7)
(2.7)
Отклонения 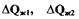 определяем разложением нелинейных
определяем разложением нелинейных
зависимостей 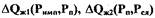 в ряд Тейлора и удержанием первых
в ряд Тейлора и удержанием первых
членов. С учетом того, что 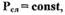 имеем :
имеем :
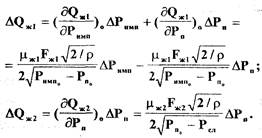 ■9
■9
Расход 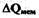 рассчитаем по формуле
рассчитаем по формуле
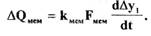
Записав уравнение (2.7) в безразмерных параметрах,получим следующее выражение (с учетом равенства 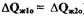 ):
):
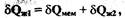 (2.8)
(2.8)
-55-где 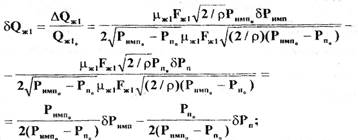
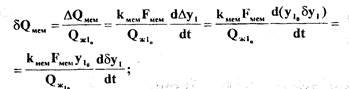
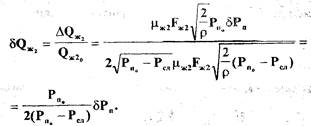
Подставив выражения для 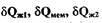 в равенство (2.8), получим
в равенство (2.8), получим
уравнение:

или, перегруппировав члены, получим:
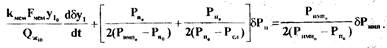 (2.9)
(2.9)
-56
-Из уравнения равновесия мембраны со струйной трубкой выразим давление 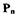 через перемещение
через перемещение 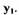 Пренебрегая силами инерции подвижных частей, запишем уравнение баланса сил, действующих на шток мембраны:
Пренебрегая силами инерции подвижных частей, запишем уравнение баланса сил, действующих на шток мембраны:
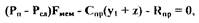
где 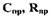 - жесткость и усилие предварительной затяжки пружины струйной
- жесткость и усилие предварительной затяжки пружины струйной
трубки соответственно.
Переписав последнее выражение в малых отклонениях параметров, имеем (с учетом 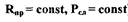 ):
):
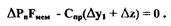
Или, записав данное уравнение в безразмерных отклонениях, получим:
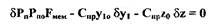
или
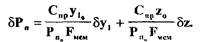
Подставив последнее уравнение в выражение (2.9), получим:
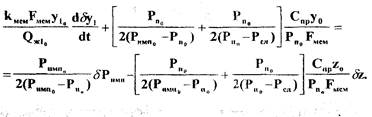
Или в стандартной форме
-57-
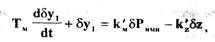 (2.10)
(2.10)
где 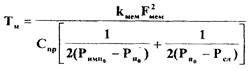 - постоянная времени узла
- постоянная времени узла
мембраны;
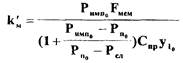 - коэффициент усиления узла мембраны;
- коэффициент усиления узла мембраны;
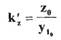 - коэффициент усиления узла мембраны по координате. Учитывая то, что координата среза сопла струйной трубки у прямо
- коэффициент усиления узла мембраны по координате. Учитывая то, что координата среза сопла струйной трубки у прямо
пропорциональна координате штока 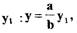 где
где  - расстояние от
- расстояние от
неподвижного шарнира до среза сопла и до крепления мембраны соответственно (см.рис.2.1), в отклонениях последнее равенство преобразуем к виду:
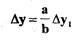
или

где 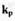 - коэффициент усиления рычага.
- коэффициент усиления рычага.
С учетом последнего уравнения равенство (2.10) можно переписать относительно координаты у:
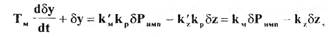 (2.11)
(2.11)
-58-
где 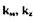 - коэффициенты усиления узла мембраны с учетом рычага.
- коэффициенты усиления узла мембраны с учетом рычага.
Уравнение нелинейной расходной характеристики струйного усилителя Действие струйного усилителя основано на преобразовании кинетической энергии быстро движущейся струи жидкости в потенциальную энергию давления, которое используется в исполнительном механизме для перемещения поршня 9 (см.рис.2.1). Входным сигаалом усилителя является смещение среза сопла у, а выходным - расход рабочего тела 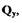 затраченный на перемещение поршня исполнительного механизма. Зависимость
затраченный на перемещение поршня исполнительного механизма. Зависимость 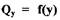 (рис.2.2) является существенно нелинейной, что объясняется наличием, во-первых, перемычки между приемными соплами, обуславливающей зону нечувствительности шириной
(рис.2.2) является существенно нелинейной, что объясняется наличием, во-первых, перемычки между приемными соплами, обуславливающей зону нечувствительности шириной 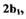 и, во-вторых, зоны насыщения при
и, во-вторых, зоны насыщения при 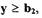 причем диаметр приемного сопла больше, чем диаметр сопла струйной трубки. Безразмерная нелинейная характеристика
причем диаметр приемного сопла больше, чем диаметр сопла струйной трубки. Безразмерная нелинейная характеристика 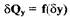 показана на рис.2.2.
показана на рис.2.2.
Зависимость 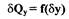 может быть описана следующим выражением:
может быть описана следующим выражением:
 (2.12)
(2.12)
где 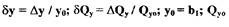 - базовые значения координаты у
- базовые значения координаты у
и расхода 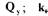 , - коэффициент угла наклона линейного участка
, - коэффициент угла наклона линейного участка
характеристики 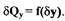 Для определения
Для определения 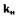 запишем зависимость расхода рабочей среды в приемном канале струйного усилителя:
запишем зависимость расхода рабочей среды в приемном канале струйного усилителя:
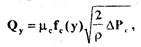 (2.13)
(2.13)
-59-
- 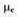 - коэффициент расхода;
- коэффициент расхода; 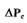 - перепад давления на усилителе;
- перепад давления на усилителе; 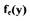
нелинейная зависимость проходного сечения усилителя от координаты у, по форме совпадающая с зависимостью 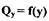
Полагая 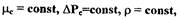 определим малое отклонение
определим малое отклонение 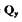
относительно его установившегося значения :
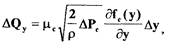
Где 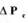 - установившееся значение перепада давления на усилителе;
- установившееся значение перепада давления на усилителе; 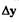
отклонение координаты у от установившегося значения.
Переходя к безразмерным отклонениям  получаем:
получаем:
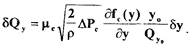
Из последнего выражения определяем значение коэффициента 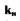 как сомножителя перед §у :
как сомножителя перед §у :
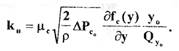
Уравнение исполнительного механизма (сервопоршня) При выводе уравнения предполагаем, что силы трения и инерции отсутствуют, а жидкость несжимаема. При данных допущениях уравнение движения сервопоршня выводится из уравнения баланса расходов:
 (2.14)
(2.14)
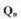 - объемный расход рабочей среды, вытесняемый сервопоршнем при Своем движении , определяемый из выражения:
- объемный расход рабочей среды, вытесняемый сервопоршнем при Своем движении , определяемый из выражения:
-60-
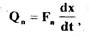 (2.15)
(2.15)
где 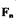 - площадь торца поршня,
- площадь торца поршня, 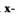 осевая координата поршня.
осевая координата поршня.
Последнее выражение в размерных и безразмерных отклонениях запишется в следующем виде:
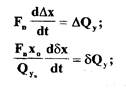
или
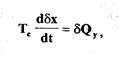 (2.16)
(2.16)
где 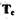 - постоянная времени сервопоршня.
- постоянная времени сервопоршня.
Равенство (2.16) представляет собой уравнение движения сервопоршня.
Уравнение парового клапана Объемный расход пара через регулирующий клапан определяется следующими зависимостями (считаем режим истечения пара из клапана критическим):
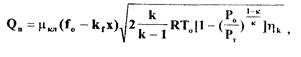 (2.17)
(2.17)
где 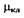 - коэффициент расхода;
- коэффициент расхода; 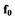 - площадь проходного сечения клапана при
- площадь проходного сечения клапана при  - коэффициент пропорциональности, связывающий площадь проходного сечения клапана с его смещением
- коэффициент пропорциональности, связывающий площадь проходного сечения клапана с его смещением 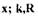 - коэффициенты адиабаты
- коэффициенты адиабаты
и газовая постоянная пара; 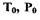 - температура и давление пара на входе в
- температура и давление пара на входе в
клапан;  - давление пара на входе в турбину;
- давление пара на входе в турбину;  - адиабатический
- адиабатический
коэффициент потерь на клапане.
-61 –
Приняв допущения о том, что при малых отклонениях клапана иярлметры пара остаются неизменными, перепишем уравнение (2.1) относительно отклонений параметров 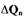 и
и 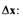

Перейдя к безразмерным параметрам 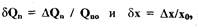 получим выражение:
получим выражение:
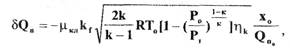
или
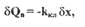 (2.18)
(2.18)
ГДе 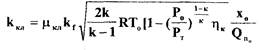 - коэффициент усиления
- коэффициент усиления
клапана.
Построение структурной схемы САР
Система полученных уравнений звеньев САР (уравнения (2.4), (2.5), (2.1 1), (2.12), (2.16), (2.18)) имеет вид :
 (2.19)
(2.19)
-62-
Для построения структурной схемы САР уравнения (2.!9) запишем в операторной форме:
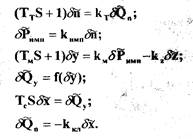 (2.20)
(2.20)
В уравнениях (2.20) 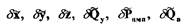 - изображения параметров по Лапласу.
- изображения параметров по Лапласу.
В соответствии с данной системой уравнений строим структурную схему (см.рис.2.3).
Исследуем устойчивость состояния равновесия САР приближенными методами (алгебраическим и частотным), а также определим параметры автоколебаний моделированием переходных процессов в системе с помощью пакета программ СИАМ. Значения параметров системы примем равными:
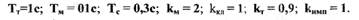

Рис.2.3. Структурная схема САР
-63 -
2.3. Определение параметров автоколебаний в САР
алгебраическим способом
Выделив из структурной схемы САР (рис.2.3) нелинейное звено, запишем дифференциальное уравнение остальной (линейной) части системы и операторной форме:
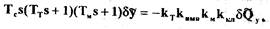 (2.21)
(2.21)
Определим для нелинейного звена гармонически линеаризованное ныражение
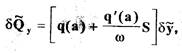 (2.22)
(2.22)
причем для данной нелинейности (см.рис.2.2) согласно прил. 1 имеем:
 (2.23)
(2.23)
Решая совместно уравнения (2.21) и (2.22) , получим линеаризованное уравнение замкнутой нелинейной системы:
 (2.24) где
(2.24) где 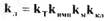 - коэффициент усиления линейной части системы.
- коэффициент усиления линейной части системы.
-64-
Для отыскания существования периодического решения 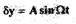 уравнения (2.24) в характеристический полином
уравнения (2.24) в характеристический полином
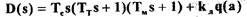
подставим 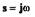 , выделим вещественную и мнимую части и приравняем их
, выделим вещественную и мнимую части и приравняем их
к нулю:
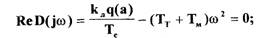 (2.25)
(2.25)
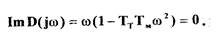 (2.26) Из уравнения (2.26) находим частоту периодического решения
(2.26) Из уравнения (2.26) находим частоту периодического решения
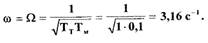
Подставив значение 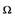 в уравнение (2.25), получаем выражение:
в уравнение (2.25), получаем выражение:

откуда
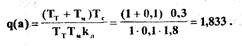 (2.27)
(2.27)
Ввиду сложности зависимости  (см. формулу (2.23)) уравнение
(см. формулу (2.23)) уравнение
(2.27) решаем графически, причем для удобства решения целесообразно
- 65 -
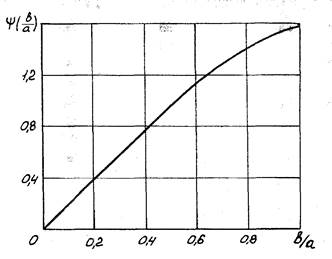 Рис.2.4. График зависимости
Рис.2.4. График зависимости 
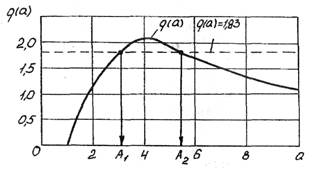 Рис.2.5. Графическое решение уравнения
Рис.2.5. Графическое решение уравнения 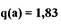
-66-
построить график функции  изображенный на
изображенный на
рис. 2.4. Тогда выражение для зависимости существенно упрощается
 (2.28)
(2.28)
По уравнениям (2.28) строим графическую зависимость 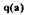 (см.рис.2.5), по точкам пересечения которой со значением
(см.рис.2.5), по точкам пересечения которой со значением 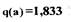 определяем возможные амплитуды колебаний:
определяем возможные амплитуды колебаний: 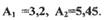 Отметим
Отметим
здесь, что график функций 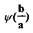 (рис.2.4) удобно использовать при анализе и
(рис.2.4) удобно использовать при анализе и
некоторых других нелинейностей.
Для исследования устойчивости найденных периодических решений используем приближенное аналитическое условие для устойчивого решения (см.рис.1.3)
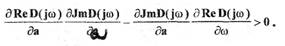
Из выражений (2.25) и (2.26) находим
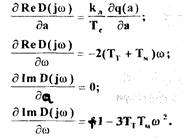
-67-
Подставив в последнее выражение 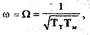 перепишем условие
перепишем условие
устойчивости в виде:
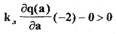 или
или 
т.е. частная производная 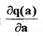 должна быть отрицательной. Из графика q(a)
должна быть отрицательной. Из графика q(a)
(см.рис.2.5) видно, что это условие имеет место при 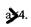 Следовательно,
Следовательно,
периодическое решение 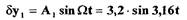 является
является
неустойчивым, а решение 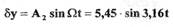 - устойчивым.
- устойчивым.
2.4. Исследование устойчивости и автоколебаний в САР частотным методом (методом Гольдфарба)
Для определения параметров и устойчивости автоколебаний по методоу Гольдфарба выделяем линейную часть системы и нелинейное звено, т.е. представляем САР частоты вращения в следующем виде (см.рис.2.6).
Построим АФЧХ линейной части системы 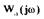 и годограф
и годограф
гармонически линеаризованного нелинейного звена - 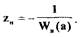
Согласно структурной схеме АФЧХ линейной части системы:
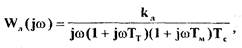
ее модуль
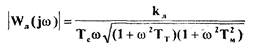
и фаза
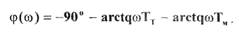
-68-
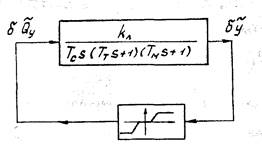
Рис.2.6. Структурная схема САР при определении параметров автоколебаний методом Гольдфарба
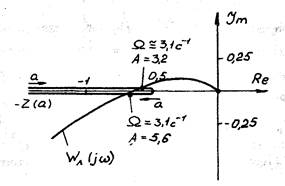
Рис.2.7. К определению амплитуды и частоты автоколебаний САР турбопривода методом Гольдфарба
-69-
Задаваясь значениями 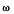 от 0 до
от 0 до 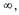 строим АФЧХ линейной части системы
строим АФЧХ линейной части системы 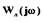 . При этом можно, например, воспользоваться программой
. При этом можно, например, воспользоваться программой
RADIS [6].
Передаточная функция нелинейного звена 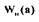 определяется по
определяется по
формулам (2.23).
Учитывая сложность формул, воспользуемся графически зависимостью 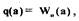 изображенной на рис. 2.5, и построим обратную зависимость
изображенной на рис. 2.5, и построим обратную зависимость
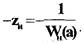 Годограф -
Годограф - 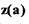 лежит на отрицательной полуоси и имеет
лежит на отрицательной полуоси и имеет
две ветви: одна ветвь соответствует амплитудам 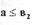 , вторая - амплитудам
, вторая - амплитудам
большим 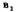 . Отметим, что зависимость имеет
. Отметим, что зависимость имеет 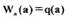 максимум
максимум
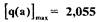 при
при 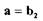 (см.рис.2.5). Минимальное значение модуля
(см.рис.2.5). Минимальное значение модуля
функции 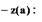
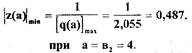
Из рис. 2.7 видно, что годографы 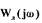 и
и 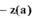 пересекаются в двух
пересекаются в двух
точках, соответствующих одной частоте 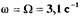 и двум амплитудам
и двум амплитудам
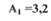 и
и 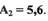 Это означает, что это уравнение
Это означает, что это уравнение
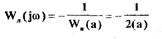
имеет два периодических решения
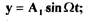 (2.29)
(2.29)
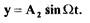 (2.30)
(2.30)
-70-
Исследуем данные решения на устойчивость по виду охвата АФЧХ 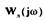 годографа —
годографа — 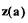 . Для того чтобы периодическое решение было
. Для того чтобы периодическое решение было
устойчивым, требуется, чтобы W^jce) охватывала часть годографа — 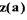 соответствующую меньшим амплитудам. Поэтому решение (2.29) является неустойчивым, а решение (2.30) - устойчивым.
соответствующую меньшим амплитудам. Поэтому решение (2.29) является неустойчивым, а решение (2.30) - устойчивым.
2.5. Моделирование САР с помощью пакета программ СИАМ. Оценка результатов исследования САР
Система автоматизированного моделирования и параметрической оптимизации СИАМ предназначена для решения широкого круга задач исследования динамических систем на персональной ЭВМ. Подробно с работой системы можно ознакомиться по работе [7] или по справочной службе самой системы. Важным достоинством системы является наглядность представления САР в виде структурных схем, элементами которых являются типовые блоки СИАМ. В библиотеке блоков СИАМ» кроме всех типовых линейных звеньев САР имеется широкий набор нелинейных блоков, позволяющих моделировать практически любые известные нелинейные характеристики.
Для моделирования нелинейной САР необходимо, во-первых, с помощью режима ввода (нажав функциональную клавишу F2) задать структурную схему САР (установив в СИАМ соответствующие блоки и связи между ними) и , во-вторых , в режиме имитационного моделирования (функциональная клавиша F7) произвести построение переходной характеристики САР. Непосредственно перед моделированием необходимо выбрать метод численного интегрирования (методы Эйлера, Рунге-Кутта, Кутта-Меерсона или Фельберга), пределы интегрирования, а также допустимую погрешность. Наиболее точным является метод Фельберга, хотя при этом процесс счета наиболее длителен.
-71 -
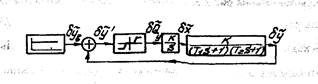
Рис.2.8. Набранная в СИАМе структурная схема САР частоты вращения турбопривода
Рие.2.9. Зависимость изменения координаты среза сопла струйной трубки у от времени
-72-
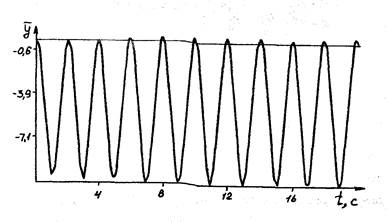
Набранная в системе СИАМ САР частота вращения трубопривода имеет вид, изображенный на рис.2.8. Результаты моделирования (по сигналу смещения сопла струйного усилителя 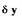 ) представлены на рис.2.9. Как
) представлены на рис.2.9. Как
видно из переходной характеристики 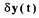 , в САР устанавливаются
, в САР устанавливаются
устойчивые автоколебания с частотой 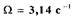 (0,5 Гц) и амплитудой
(0,5 Гц) и амплитудой
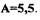
Рассчитаем погрешность определения частоты и амплитуды автоколебаний. При этом полагая, что результаты моделирования адекватны реальным процессам (погрешностью счета пренебрегаем), оценим погрешность алгебраического и частотного способов по формулам:
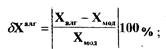
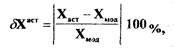
где 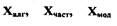 - параметры автоколебаний, определенные
- параметры автоколебаний, определенные
алгебраическим, частотным способами и моделированием соответственно. Для рассмотренной САР частоты вращения имеем:

-73-
Анапиз погрешности показывает, что определение параметров произведено с достаточной точностью, причем погрешностьчастотного метода «двое превышает погрешность алгебраического метода. Это связано, видимо, с более грубым определением параметров точки пересечения годографов
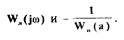
В заключение отметим, что для устранения автоколебаний в САР турбопривода можно уменьшить общий коэффициент усиления линейной части 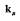 до значения 1,61 (и ниже). Последнее значение определяется из условия:
до значения 1,61 (и ниже). Последнее значение определяется из условия:
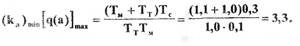
Откуда 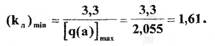
Можно также предложить снизить крутизну характеристики нелинейного элемента 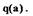
-74-Библиографический список
1. Иващенко Н.Н. Автоматическое регулирование М.: Машиностроение ,
1978.-736 с.
2. Черкасов Б.А Автоматика и регулирование ВРД.- М.: Мапшностроение,
1988.- 360 с.
3. Попов Е.П. Прикладная теория процессов управления в нелинейных
системах М.: Наука, 1973.- 584 с.
4. Бесекерский В.А., Попов Е.П. Теория систем автоматического
регулирования . -М.: Наука, 1975. - 768 с.
5. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. - М.: Наука, 1969.- 588 с.
6. Гимапяев А.Г. Динамические характеристики систем автоматического регулирования : Учебное пособие. - Куйбышев : КуАИ, 1986- 60 с .
7. Система автоматизированного моделирования и параметрической
оптимизации: Руководство пользователя / Сост. А.Ф Малеев. Самара,
Самар. гос. аэрокосмический университет, 1993. - 37 с.
-75-
Приложение 1 -коэффициенты гармонической линеаризации основных нелинейных элементов САР
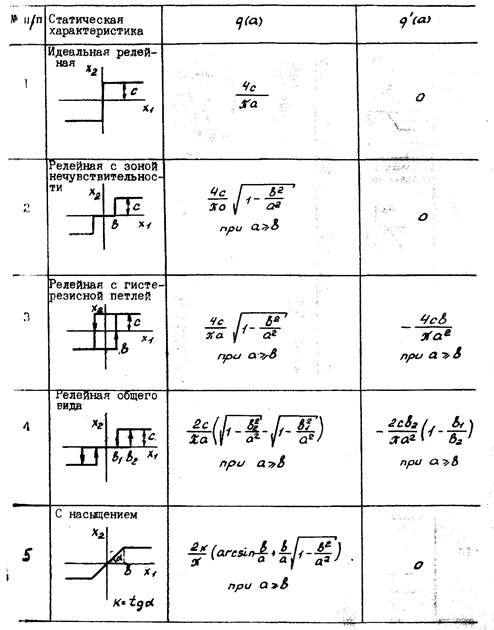
- 76 -
Окончание прил. I

-77-
Приложение 2 Задачи для самостоятельного решения
1. Построить фазовую траекторию переходного процесса, изображенного на рис. П2.1.
2. Представить графически вид переходного процесса по фазовой траектории , показанной на рис. П 2.2.
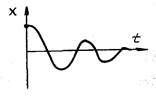
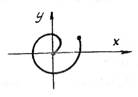
Рис. П 2.1 Рис. П 2.2
3. Преобразовать структурную схему (рис. П 2.3) при наличии в ней нелинейного звена 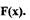
4. Построить фазовую траекторию, если система описывается уравнением
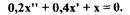 (
( 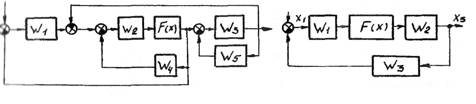
Рис. П 2.3 Рис. П 2.4
5. Получить дифференциальное уравнение нелинейной САУ (рис. П 2.4),
если известно, что 
-78- Продолжение
6. Изобразить, как будет изменяться положение штока порашя привода направляющих аппаратов компрессора (рис.П.2.5,а) при известном изменении 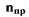 (рис.2.5,6) и характеристике гидропривода, представленной в прил.1 под номером 3.
(рис.2.5,6) и характеристике гидропривода, представленной в прил.1 под номером 3.
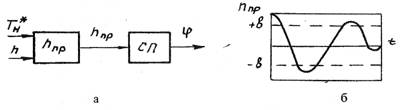
Рис. П 2.5 7.0пределить возможность возникновения автоколебаний, если известно расположение характеристик линейного и нелинейного элементов на комплексной плоскости (рис. П 2.6). При лом 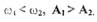
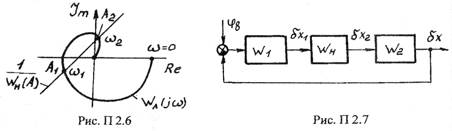
8. Для структурной схемы, изображенной на рис. П 2.7, определить
параметры автоколебательного режима, если 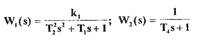
и нелинейное звено представляет собой идеальное реле (характеристика №1 прил.1).
9. Для известной линейной части нелинейной системы (задача 8)
определить параметры автоколебательного режима при наличии звена,
имеющего релейную характеристику с зоной нечувствительности (см.
прил. 1, характеристика №2).
-79- Продолжение прил.2
10. Определить возможность существования устойчивых колебаний в
системе, если линейная ее часть имеет передаточную функцию следующего вида:
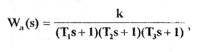
а нелинейная часть представлена двухпозиционным реле (см. прил.1, характеристика № 3).
11. Определить граничное значение коэффициента усиления линейной
части  при котором в системе возникают автоколебания. Линейная часть
при котором в системе возникают автоколебания. Линейная часть
системы имеет передаточную функцию:
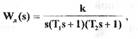
а нелинейная характеристика приведена в прил.1, №6, причем для нелинейного звена 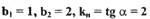 (задачу решить алгебраическим и
(задачу решить алгебраическим и
частотным способами).
12. Исходя из уравнения линейной части САР
(T,s + l)sx, = -клх2
и уравнения нелинейного звена:
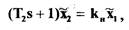
где 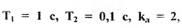 а зависимость
а зависимость 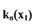 соответствует
соответствует
характеристике №5 (прил.1), где 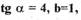 определить все периодические
определить все периодические
решения и с помощью аналитического критерия определить, какое из них
устойчивое.
13. Исследовать устойчивость состояния равновесия нелинейной
> иегемы, структурная схема которой изображена на рис. П 2.8, если заданы
- 80 –
Окончание прил. параметры нелинейного эвена (прил.1, №2) 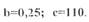 Задачу решить
Задачу решить
методом Гольдфарба.

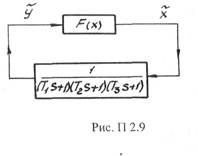
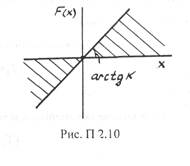
Рис. П 2.8 14. Структурная схема нелинейной САР изображена на рис. П 2.9. Коэффициент передачи линейной части САР и нелинейного звена 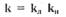 условно отнесен к линейному звену. Определить, используя критерий В.М.Попова, при каких значениях к система будет абсолютно устойчива, если характеристика нелинейного звена расположена в секторе (0, к) (рис. П 2.10).
условно отнесен к линейному звену. Определить, используя критерий В.М.Попова, при каких значениях к система будет абсолютно устойчива, если характеристика нелинейного звена расположена в секторе (0, к) (рис. П 2.10).
Учебное издание
Крючков Александр Николаевич Шахматов Евгений Владимирович 111орин Владимир Павлович
I имадиев Асгат Гатьятович
Анализ устойчивости и автоколебаний в нелинейных системах управления
Учебног пособие
Редактор Т.И. Кузнецова
II у II.редактор Г.А. Усачева
I "Рректор Т.И. Кузнецова
Ипцензия ЛР№020301 от 30.12.96
I [одписано в печать 27.04.98.
Формат 60X84 1/16. Бумага офсетная. Печать офсетная. \'< и.п.л. 4,7. Усл.кр.-отт. 4,8. Уч.-изд.л. 4,6. I мрнж 100 >кз. Заказ 57,
i 1м,||н кий государственный аэрокосмический умиигргтсг мм. академика СП. Королева. I I КЖ6 ('.iM.ip.i, Московское шоссе, 34. IIIMH'I АУ 443001 Самара, ул. Молодогвардейская, 151.
Дата добавления: 2021-01-21; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
