Нормальный закон распределения

Лекция на 13.11.2020 г.

Числовые характеристики случайной величины

Функция распределения вероятностей полностью описывает случайную величину с вероятностной точки зрения. Однако во многих практических задачах нет необходимости строить закон распределения, достаточно бывает указать лишь отдельные числовые характеристики, до некоторой степени характеризующие существенные черты распределения случайной величины.

Такие характеристики, назначение которых – выразить в сжатой форме наиболее существенные особенности распределения, называют числовыми характеристиками случайной величины.

В качестве основных числовых характеристик случайной величины выступают, так называемые, моменты случайной величины. Чаще всего применяются моменты двух видов: начальные и центральные. Для дискретной случайной величины начальный момент k – ого порядка определяется формулой:

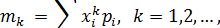
для непрерывной случайной величины – формулой

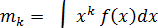
Начальный момент первого порядка (k =1) называется математическим ожиданием (средним значением) случайной величины. Математическое ожидание принято обозначать различным образом:

Для дискретных случайных величин

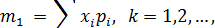
Для непрерывных

Пользуясь знаком математического ожидания, можно объединить формулы для моментов k-ого порядка:

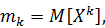
Т.е. начальным моментом k-ого порядка случайной величины Х называется математическое ожидание k-й степени этой случайной величины.

Перед тем, как дать определение центрального момента, введем понятие центрированной случайной величины.

Пусть имеется случайная величина Х с математическим ожиданием m_x. Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от ее математического ожидания:

Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю. Центрирование случайной величины равносильно переносу начала координат в среднюю точку, абсцисса которой равна математическому ожиданию.

Моменты центрированной случайной величины называются центральными. Центральный момент k-ого порядка для дискретной случайной величины определяется формулой

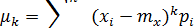
для непрерывной случайной величины

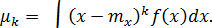
Таким образом, центральным моментом порядка k случайной величины Х называется математическое ожидание k-ой степени соответствующей центрированной случайной величины:

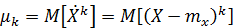
Первый центральный момент всегда равен нулю.

Второй центральный момент называется дисперсией. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

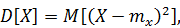
Для дискретной случайной величины

для непрерывной

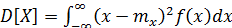Другие обозначения для дисперсии: Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Поэтому часто используется среднее квадратическое отклонение (СКО или стандарт), равное квадратному корню из дисперсии и обозначаемое .

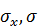Математическое ожидание и дисперсия наиболее часто используемые числовые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения используются моменты высших порядков.

Нормальный закон распределения

Из всех изученных к настоящему времени случайных величин, наиболее часто при обработке экспериментальных данных исследователи используют нормальное (Гауссово) распределение. Отметим, что согласно центральной предельной теореме, которая гласит , что при определенных условиях распределение нормированной суммы n независимых случайных величин, распределенных по произвольному закону, стремится к нормальному при n стремящемся к бесконечности. Условия, при которых теорема оказывается справедливой, состоят в том, что различные случайные величины должны иметь конечные дисперсии и дисперсия любой случайной величины не должна быть слишком большой по сравнению с дисперсиями других.

При обработке экспериментальных данных эта теорема имеет очень большое значение, поскольку отклик является случайной величиной в результате влияния неконтролируемых факторов, число которых, в общем случае, стремится к бесконечности.

Следовательно, если при планировании эксперимента учтены все наиболее существенные факторы и затем, при проведении опытов, они контролируются, то при обработке экспериментальных данных можно предполагать, что отклик не должен противоречить нормальному закону распределения.

Большинство других распределений (Стьюдента, Фишера, Кохрена, Пирсона и др.), которые используются в математической статистике, получены на основе нормального распределения.

Но с другой стороны, нельзя абсолютизировать значение нормального закона. Не все случайные величины распределены по нормальному закону. Но если явление подвержено многим случайным факторам, то их суммарное воздействие можно описать с помощью нормального закона.

Как отмечалось ранее, для случайной величины, не противоречащей нормальному закону, функция распределения задается формулой

а соответствующая ей плотность распределения имеет вид:

и определяется двумя параметрами - математическим ожиданием и 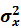- дисперсией. На рис.5.9 показан график плотности распределения вероятности нормального закона – кривая распределения, которая называется нормальной кривой или кривая Гаусса.

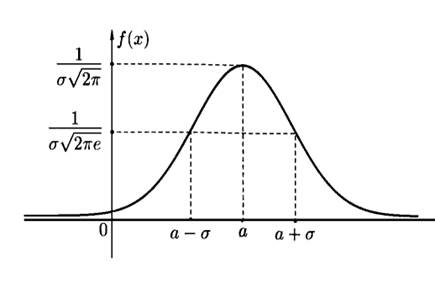Рисунок 5.9 - Кривая Гаусса

Основные свойства нормального закона распределения:

1. Кривая плотности распределения симметрична относительно значения , называемого центром распределения.

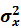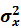2. При больших значениях кривая более пологая, т.е. является мерой величины рассеивания значения случайной величины около значения .

3. Максимум ординаты кривой плотности распределения определяется выражением .

4. Можно убедиться, что точки и 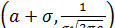являются точками перегиба графика функции .

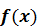5. Для нормального распределения математическое ожидание, мода и медиана совпадают.

В ряде случаев удобно рассматривать не саму случайную величину, а ее отклонение от математического ожидания:

Такая случайная величина называется центрированной. Отношение случайной величины к ее среднему квадратическому отклонению 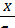называется нормированной случайной величиной.

Очевидно, что математическое ожидание центрированной случайной величины равно нулю, а дисперсия нормированной случайной величины – единице.

Приведенная (стандартная) случайная величина – это центрированная и нормированная случайная величина

Математическое ожидание и дисперсия приведенной случайной величины равны соответственно, нулю и единице. Нормальное распределение с и называется стандартным и обозначается .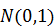

Для приведенной случайной величины нормальное стандартное распределение принимает вид

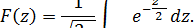
На рис. 5.10 показаны функция распределения и плотноcть нормального закона распределения вероятности.

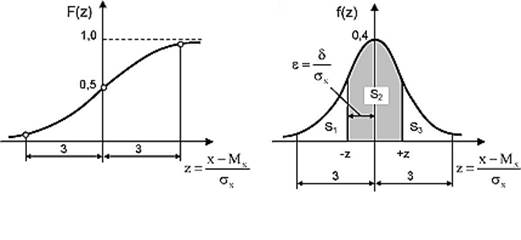
Рисунок 5.10 - Основные свойства нормального распределения

Значения нормированной функции нормального распределения табулированы и приведены в различных учебниках и справочниках. Отметим, что иногда вместо функции табулируется функция

Т.к. 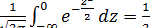(известный в математике интеграл Пуассона), то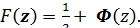

Функция нечетная, т.е.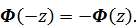

В ряде случаев важно знать, что случайная нормально распределенная величина X не будет отличаться от своего математического ожидания не больше , чем на величину ε:

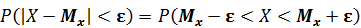Выразив вероятность через плотность вероятности, получим

Для приведенной случайной величины

Т.к. ,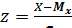

Обозначив 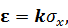получим .

Поскольку табулированная функция, то ее значения можно определить для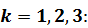

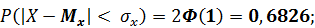
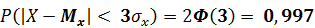
Таким образом, для нормально распределенной случайной величины вероятность того, что она примет такое значение, которое не будет отличаться от ее математического ожидания более чем на одно СКО, равна 0,68. Т.е. при нормальном распределении примерно 2/3 всех значений случайной величины лежит в интервале 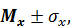а 95% значений случайной величины лежат в диапазоне 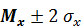. Интервалу 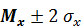соответствует вероятность 0,95, а интервалу - вероятность 0,997.

Следовательно, отличие какого-либо из значений нормально распределенной случайной величины от ее математического ожидания не превосходит утроенного среднего квадратического отклонения с вероятностью 0.99. Это свойство нормально распределенной случайной величины носит название «правило трех сигм».

Дата добавления: 2020-12-12; просмотров: 55; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!