Влияние способа закрепления концов стержня

РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ

Устойчивые и неустойчивые формы равновесия

Равновесие абсолютно твердого тела может быть устойчивым, безразличным и неустойчивым. Например, шар, расположенный на вогнутой поверхности (рис.13.1, а), находится в состоянии устойчивого равновесия. Если его отклонить в сторону и предоставить самому себе, то он возвратится в исходное положение. Шар, расположенный на горизонтальной поверхности (рис. 13.1, б), находится в состоянии безразличного равновесия. Если произ-вести его отклонение, то он не возвращается в исходное положение, но и не продолжает движение. Шар, расположенный на выпуклой поверхности (рис. 13.1, в), находится в состоянии неустойчивого равновесия. Если его отклонить в сторону и предоставить самому себе, то он, не возвращаясь в исходное положение, продолжает движение.

а б в

Рис. 13.1

Аналогично можно рассматривать проблему устойчивости и для деформируемого тела. Например, длинный стержень, нагруженный вдоль оси сжимающей силой, также может иметь три формы равновесия, которые зависят от величины силы. Ее критическое значение F_cr определяет граничное состояние. При F < F_cr стержень находится в состоянии устойчивого равновесия (рис. 13.2, а). Отклоненный в сторону и предоставленный затем самому себе, он возвращается в первоначальное прямолинейное состояние.

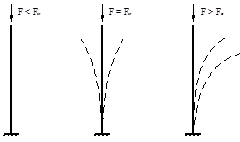а б в

Рис. 13.2

При критической силе стержень теряет способность сохранять прямо-линейную форму равновесия (рис 13.2, б). Получив отклонение, он сохраняет его после устранения причины отклонения, т.е. находится в состоянии безразличного равновесия.

При F > F_cr прямолинейная форма равновесия стержня становится неустойчивой (рис. 13.2, в). Отклоненный в сторону и предоставленный затем самому себе, он продолжает искривляться.

Отклонение стержня от исходного состояния предполагает его искривление. На практике причиной этому могут быть действие силы с некоторым эксцентриситетом или начальная кривизна стержня. Пока сжимаю-щая сила меньше критической, перемещения точек стержня будут небольшими, вследствие чего он сохраняет принимаемую за прямолинейную форму равновесия.

Когда сила превышает порог критического значения, упомянутые перемещения чрезвычайно быстро возрастают, вследствие чего прямолинейная форма равновесия стержня становится неустойчивой.

Таким образом, теоретически неограниченный рост перемещений при ограниченном росте сжимающей силы может быть принят за критерий потери устойчивости. Практически, неограниченный рост перемещений приостанавливается вследствие исчерпания прочности материала.

Потеря устойчивости возможна также при изгибе, кручении и сочетании отдельных видов деформаций.

Формула Эйлера для критической силы

Обратимся к шарнирно опертому стержню, на который действует сжимающая сила, достигая критического значения (рис. 13.3). Допускаем отклоненное состояние в плоскости наименьшей жесткости. При однородном материале поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение.

Рис. 13.3

Используем приближенное дифференциальное уравнение изогнутой оси стержня:

EI_min(d²v/dx²) = M .

Величина момента определяется по формуле

M = – F_crv .

Минус введен для согласования знаков M и v. Таким образом,

EI_min(d²v/dx²) = – F_crv,

или

(d²v/dx²) + α²v = 0,

где α²= F_cr /(EI_min).

Общее решение линейного дифференциального уравнения второго порядка имеет вид:

v = A cosαx +B sinαx,

где А и В – постоянные интегрирования, для определения которых используются граничные условия: 1) при x = 0, v = 0; 2) при x = l , v = 0.

Из первого условия получаем А = 0. Следовательно, v = Bsin αx . Из второго условия получаем B sinαl = 0. Следовательно, sinαl = 0. Из ряда значений αl = 0,π, 2π,…, nπ, где n – любое целое число, выбираем значение π, дающее наименьшую критическую силу.

Принимая αl = π, α²l² = π², α² =π²/ l²,находим:

F_cr = (π²EI_min)/l².

Эту формулу впервые вывел Л. Эйлер в 1744 г.

Постоянная В остается неопределенной вследствие принятия приближенного дифференциального уравнения изогнутой оси бруса.

Влияние способа закрепления концов стержня

На критическую силу

На рис. 13.4 показаны другие случаи закрепления концов стержня. Каждую из этих задач можно решать по плану, реализованному для шарнирно опертого стержня. В то же время решение можно получить путем сопоставления изгиба шарнирно опертого стержня с изгибом стержня при другом закреплении его концов (штриховые линии на рис. 13.4) Обобщенная формула:

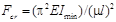
содержит так называемый коэффициент приведенной длины μ.

Приведенная (свободная) длина l₀ = μl может быть истолкована как некоторая условная длина однопролетного стержня, критическая сила которого при шарнирном закреплении его концов такая же, как для заданного стержня. Понятие о приведенной длине впервые введено профессором Петербургского института инженеров путей сообщения Ф.С. Ясинским в 1892 г.

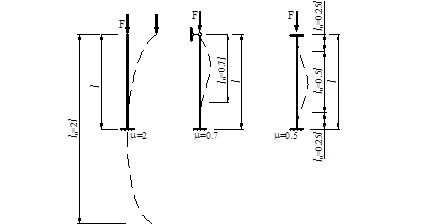
Рис. 13.4

Исследования показали, что местные ослабления (заклепочные отверстия, уменьшение сечения за счет врубок и т.п.) существенно не влияют на величину критической силы. Поэтому в формулу для F_cr входит момент инерции I_br площади сечения без учета ослабления A_br (брутто). При вычислении критического напряжения также используется A_br:

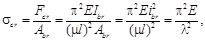
где 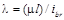– гибкость стержня (радиус инерции берется минимальный).

Вследствие использования линейного физического закона формулы для критической силы справедливы в том случае, когда напряжения σ_cr не превышают предела пропорциональности σ_pr . Из условия σ_cr = σ_pr определяется предельная гибкость λ_lim, при которой формулы еще применимы:

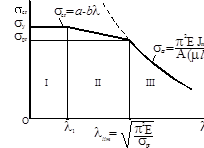λ_lim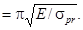

Для стали с σ_pr = 200 МПа и

Е = 2,1·10⁵МПа λ_lim ≈ 100, для чугуна λ_lim ≈ 80, для дерева λ_lim ≈ 110.

При гибкостях λ < λ₁(для стали Ст.3 λ₁=40) стержни можно рассчитывать на прочность без учёта опасности потери ус-тойчивости (рис. 13.5, зона I). Для этого случая критическими являются напряже-

ния, соответствующие предельным

Рис. 13.5 (σ_cr=σ_y).

Использование формулы Эйлера за пределами её применимости (λ < λ_l_im) приводит к завышенному расчётному значению критических напряжений, следовательно к грубым ошибкам, что чревато потерей устойчивости стержня и разрушением конструкции.

При λ < λ_l_im формулы становятся неприменимыми. В этом случае используют эмпирическую формулу Тетмайера − Ясинского (рис. 13.5, зона II):

σ_cr = а – bλ ,

где а и b – коэффициенты, зависящие от материала. Для стали Ст.3 при гибкостях λ = 40…100 коэффициенты а и b принимаются равными: а = 310 МПа, b = 1,14 МПа.

Дата добавления: 2021-01-20; просмотров: 103; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!