Правила и формулы дифференцирования
Раздел 3. Основные понятия и методы
Дифференциального и интегрального исчисления
Тема «Определение производной. Производная сложной функции» (Т9)
План лекции:
1. Задачи, приводящие к понятию «производная».
2. Приращение аргумента и функции.
3. Производная.
4. Нахождение производной функции.
5. Правила и формулы дифференцирования.
6. Производная сложной функции.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.
Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.
Определение сложному понятию «производная» мы будем давать на основании понятия более простого «Приращение функции».
|
|
|
Часто нас интересует не значение какой – либо величины, а ее изменение. Например, сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость – это отношение перемещения к промежутку времени, за который было совершено перемещение, и т. д.
Пусть дан график функции у=f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х – это изменение абсциссы от точки xo до х, т.е. ∆х = х – xo , M0М – секущая, M0N – касательная.
Рассмотрим две такие задачи.
Задача 1. Пусть дан график функции у=f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х – это изменение абсциссы от точки xo до х, т.е. ∆х = х – xo , M0М – секущая, M0N – касательная.

Найдем:
а) угловой коэффициент секущей (это средняя скорость изменения функции);
б) угловой коэффициент касательной (подсказка: касательная – это предельное положение секущей)
Решение: у= f(x) – заданная функция, ∆х = х – xo – изменениеабсциссы от точки xo до х.
vср =  . В нашем случае kсек =
. В нашем случае kсек = 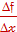
При х→х0 (или ∆х →0)будет f(x)→f(x0), следовательно, M0М→ M0N.
Тогда k асс = 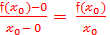 .
.
|
|
|
Задача 2. Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета – точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s. Тогда движение точки М будет описываться функцией
s = s (t), t[ t0 ; t].
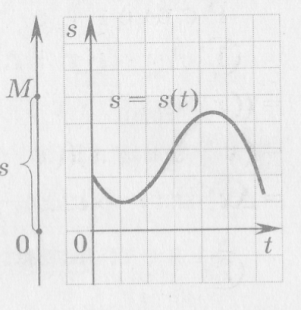
Найдем:
а) среднюю скорость за отрезок [t0 ; t];
б) скорость точки в момент времени t0 (мгновенную скорость).
Решение: За промежуток времени длительности t – t0 между моментами времени t0 и t точка проходит путь равный s(t) –s(t0 ).
Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.
Тогда vср =  ;
;
Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется число, к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн = 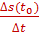 .
.
Подобные задачи рассматриваются и в экономике, и в анализе ценовой политики. Например: «цена товара напрямую зависит от расходов на производство» или «объем реализации некоторой продукции зависит от роста или снижения его цены».
А теперь давайте подведём итоги нашей исследовательской работы. Вы решали различные задачи, но все они привели к одной и той же математической модели: к числу, к которому стремиться отношение разности значений функции к разности значений аргумента. В русском языке для величины, на которую изменилось начальное количество, используется слово «прирост».
|
|
|
Приращение функции
Пусть нам дана какая- то функция y=f(x).
Проведем произвольную кривую линию и будем считать, что это график нашей функции.
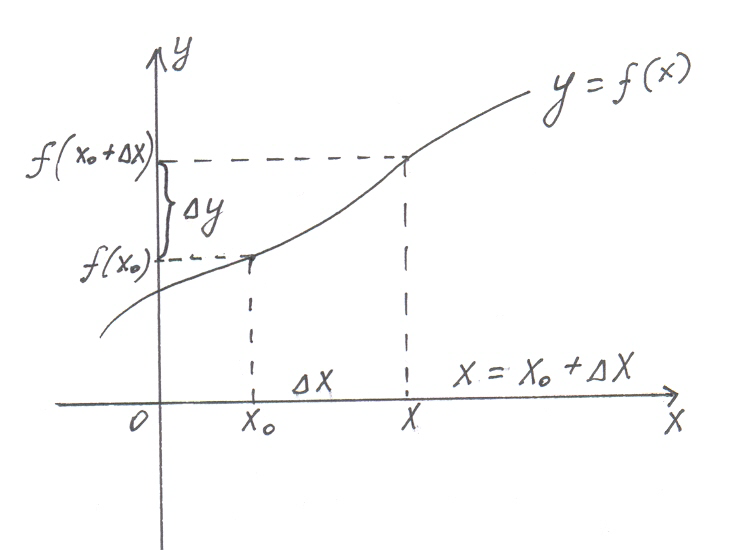
Возьмем на оси ОХ первоначальное значение аргумент обозначим его Хо. Найдем графически соответствующее ему значение функции y0= f ( x0) .
Возьмем на оси ОХ новое значение аргумента, обозначим его x. Разность между новым значением аргумента x и первоначальным x0 – это и есть приращение аргумента ∆x (дельта x).
Определение. Разность между новым значением аргумента и первоначальным называются приращение аргумента
∆х = х – х0 – приращение аргумента ( дельта икс равно икс минус икс нулевое).
Из этого равенства следует, что
x= x0+∆x
Найдем графически значение функции в точке x, то есть в точке x0+ ∆x.
Определение. Разность между новым значением функции и первоначальным называется приращением функции.
Записывается так: ∆f = f ( x0+∆x) – f ( x0).
|
|
|
F(x0+ ∆x) – новое значение функции (эф от икс нулевое плюс дельта икс).
F ( x0) – первоначальное значение функции.
∆f – приращение к функции (дельта эф).
Пример №1. Дано: f(x)=  ; X0= -2; ∆X= 0.1
; X0= -2; ∆X= 0.1
Найти приращение функции f в точке X0, т.е. ∆f.
Решение:
1. Формула ∆f = f(x0+ ∆x) – f (x0)
2. X0+ ∆X= -2+0.1=-1.9
3. f(x0+∆x)=f(-1.9)= 
4. f(x0)=f(-2)= 
5. ∆f=  ;
;
Ответ:  ;
;
Пример №2. Дано: f(x)=3x+1; x0=5;∆x=0.001.
Найти: ∆f
Решение:
1. формула ∆f = f (x0+∆x)-f(x0)
2. x0+∆x= 5+0.001=5.001;
3. f(x0+∆x)=f(5.001)=3 · 5.001+1=15.003+1=16.003;
4. f(x0)=f(5)=3· 5+1=16
5. ∆f=16.003-16=0.003
Ответ: 0,003.
Производная
Рассмотренные выше две задачи имели разные формулировки. Однако в обоих случаях мы действовали, по существу, придерживаясь одной схемы. В применении к произвольной функции f и любой точки X0 ее области определения эта схема может быть описана следующим образом.
1) с помощью формулы, задающей функции f, находим ее приращение в точке X0 :
Δf = f (х0 + Δх) – f(х0).
2) находим выражение для разностного отношения 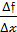 :
:
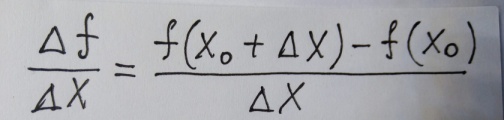 , которое затем преобразуем – упрощаем, сокращаем на Δх и т. п.
, которое затем преобразуем – упрощаем, сокращаем на Δх и т. п.
3) выясняем, к какому числу стремится 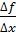 , если считать, что Δх стремится к нулю.
, если считать, что Δх стремится к нулю.
Найденное таким образом число иногда называется (по аналогии с физикой) скоростью изменения функции f в точке х0 или (что более принято) производной функции f в точке х0.
Определение. Производной функции f в точке х0 называется число, к которому стремится разностное отношение
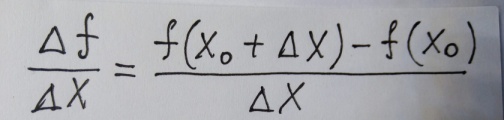
при Δх, стремящемся к нулю.
Производная функции f в точке х0 обозначается  х),
х),  у′ – эти обозначения для производной ввел Жозеф Луи Лагранж.
у′ – эти обозначения для производной ввел Жозеф Луи Лагранж.
Пример 1. Найдем производную функции f(х) = 5х + 3 в точке х0.
Будем действовать по описанной выше схеме.
1) Δf = 5(х0 + Δх) + 3 – (5х0 + 3) = раскрываем скобки
= 5х0 +5· Δх + 3 – 5х0 – 3 = проводим сокращение
= 5Δх
2) 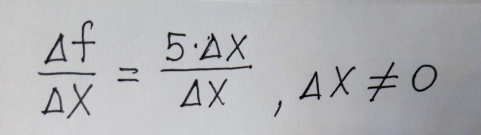 При Δх → 0 получаем, что
При Δх → 0 получаем, что  х) = 5.
х) = 5.

Пример 3. Пользуясь определением и схемой вычисления производной, найдите производную функции f(х) = х2.
Решение:
Аргументу х дадим приращение ∆х, тогда
∆f = f(x + ∆х) – f(x)=
= (x +∆х)2 – х2 =
= х2+ 2∙х∙∆х + (∆х)2 – х2 = 2∙х∙∆х + (∆х)2 = ∆х∙(2х +∆х)
= 2х = 2х.
Итак, (х2 )′ = 2х.
Рассмотрев последние два примера

 можно по аналогии записать, что
можно по аналогии записать, что
 или, например,
или, например, 
Итак, можно сделать вывод, что производная степенной функции в общем виде записывается так:
(xn) ′ = nxn-1
Пример 4. Дана функция f(x)=9. Найти производную 
Действуем по описанной выше схеме: 
По определению производной 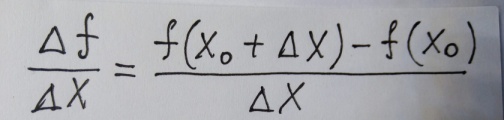 (подставляя известные значения f (х0) и f (х0 + ∆х)) получаем
(подставляя известные значения f (х0) и f (х0 + ∆х)) получаем
 = 9 – 9/ ∆х (при ∆х ≠ 0 и ∆х → 0 )
= 9 – 9/ ∆х (при ∆х ≠ 0 и ∆х → 0 )  = 0 / ∆х = 0
= 0 / ∆х = 0
Вместо 9 могло быть любое другое постоянное число, обозначим буквой С [це] (константа).
Получили формулу  - производная постоянной величины равна нулю.
- производная постоянной величины равна нулю.
Правила и формулы дифференцирования
Итак, мы уже знаем три формулы для нахождения производных:
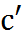 = 0 (хn)' = nxn-1 x1 = 1
= 0 (хn)' = nxn-1 x1 = 1
Пользуясь этими формулами и вспомогательными формулами действий над степенями из школьного курса.
 и
и  ,
,
выведем формулы для нахождения производных функций  и
и 
1) 
Получили формулу  (*)
(*)
Пример. 1) 
2) 
из формулы (*) следует формула 
Найдем производную функции f(x)= 
Будем использовать формулы:




Итак, получили новую формулу: производная корня квадратного имеет вид 
Правила и формулы дифференцирования следует обязательно знать, чтобы не повторять каждый раз все выкладки при нахождении данной функции. Ведь существует бесконечное множество функций и с их усложнением непосредственное дифференцирование становится все более трудоемким.
Формулы дифференцирования
| C ' =0 , | 
|
| x ' =1 , | 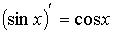
|
| (кх + b)' = к, где к и b – x числа | 
|
| (хn)' = nxn-1 | 
|

| 
|

| 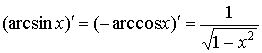
|
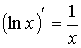
| 
|

| 
|
В таблице представлены основные формулы нахождения производных функций.
Разберем несколько примеров на нахождение производных функций с помощь. Формул, указанных в таблице.
Пример 1. Найти производную функции y = x4
Р е ш е н и е: Имеем y' = (x4)' = 4x3
Пример 2. Найти производную функции y = 3cos(x)
Р е ш е н и е: Имеем y' = (3cos(x))' = -3sin(x)
Пример 3. Найти производную функции y = tg (x)
Р е ш е н и е: Имеем 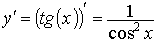
Пример 4. Найти производную функции y = arcsin (x)
Р е ш е н и е: Имеем 
Дата добавления: 2021-01-20; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
