Образец выполнения семестровой расчетно-графической работы
РОСЖЕЛДОР
Государственное образовательное учреждение
Высшего профессионального образования
«Ростовский государственный университет путей сообщения
(РГУПС)
Т.В. Клодина, Н.С. Задорожная, Н.В. Данилова
ТИПОВОЙ РАСЧЕТ ПО МАТЕМАТИКЕ
Методические указания
(1 курс, первый семестр)
Ростов-на-Дону
2011
УДК 517.2(07)+06
Клодина Т.В., Задорожная Н.С., Данилова Н.В.
Типовой расчет по математике. 1 курс, первый семестр: методические указания / Т.В. Клодина, Н.С. Задорожная, Н.В. Данилова; Рост. Гос. ун-т путей сообщения. – Ростов н/Д, 2011. - 42 с. Библиогр.: 4 назв.
Предлагаемый типовой расчет охватывает содержание разделов, изучаемых студентами в курсе «Высшая математика» в первом семестре первого курса: линейная алгебра, векторная алгебра, аналитическая геометрия на плоскости, аналитическая геометрия в пространстве, введение в математический анализ, дифференциальное исчисление.
Приведенные задания подразделяются на две группы: задачи класса «В» предназначены для хорошо и отлично успевающих студентов и класса «А» для остальных студентов.
Составлены задания с образцами решения. Практические задания разделены на 30 вариантов, предназначенных для индивидуального выполнения студентами в процессе работы над курсом. Они способствуют выработке у слушателей необходимых практических навыков в использовании теоретических положений при решении задач.
|
|
|
Типовой расчет выполняется студентами самостоятельно в течение всего семестра и подлежит защите.
Учебное пособие предназначено для студентов первого курса строительного факультета и факультета ДСМ РГУПС.
Рецензенты: канд. физ.-мат. наук, профессор В.Б. Зеленцов (РВИ РВ),
канд. техн. наук, доцент Кручинина Е.В. (РГУПС).
Задание 1.
Решить систему уравнений по формулам Крамера (задача класса “А»); методом Гаусса и матричным способом (с нахождением обратной матрицы) (задача класса «В»).
Варианты для самостоятельного решения.
| №1 | 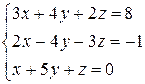
| №2 | 
| №3 | 
|
| №4 | 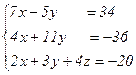
| №5 | 
| №6 | 
|
| №7 | 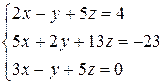
| №8 | 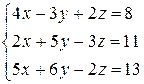
| №9 | 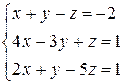
|
| № 10 | 
| № 11 | 
| № 12 | 
|
| № 13 | 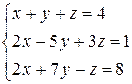
| № 14 | 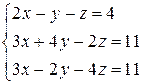
| № 15 | 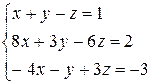
|
| № 16 | 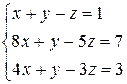
| № 17 | 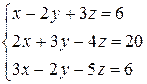
| № 18 | 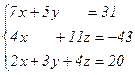
|
| № 19 | 
| № 20 | 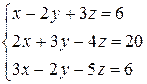
| № 21 | 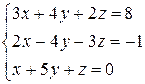
|
| № 22 | 
| № 23 | 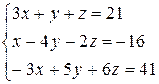
| № 24 | 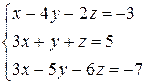
|
| № 25 | 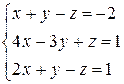
| № 26 | 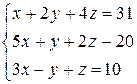
| №27 | 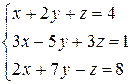
|
| № 28 | 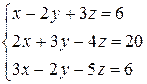
| № 29 | 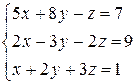
| №30 | 
|
Задание 2.
Даны вершины треугольной пирамиды: 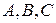 и
и  . Требуется найти:
. Требуется найти:
|
|
|
1) длину ребра 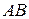 ;
;
2) площадь грани 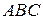 ;
;
3) угол между ребрами  и
и 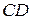 ;
;
4) объем пирамиды 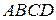 ;
;
5) уравнение плоскости 
6) уравнения высоты, опущенной из вершины  на грань
на грань 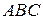 ;
;
7) уравнения стороны 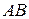 ;
;
8) длину высоты, опущенной из вершины  на грань
на грань 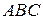 .
.
Варианты для самостоятельного решения.
| №1 |  (3;-1;5); (3;-1;5);  (4;2;3); (4;2;3);  (0;-1;1); (0;-1;1);  (-2;1;3) (-2;1;3)
| №2 |  (4;-1; 2 ); (4;-1; 2 );  (2; 3;-5 ); (2; 3;-5 );  (4;0;3); (4;0;3);  (6; 1;-1 ) (6; 1;-1 )
|
| №3 |  (0;-3;2); (0;-3;2);  (3;2;1); (3;2;1);  (5;-1;0); (5;-1;0);  (1;0;-1) (1;0;-1)
| №4 |  (1; 2; 0); (1; 2; 0);  (3;-1;0) ; (3;-1;0) ;  (01;2); (01;2);  (4;-3 ;5 ) (4;-3 ;5 )
|
| №5 |  (1; 2; 0); (1; 2; 0);  (3; -1; 6); (3; -1; 6);  (0; 4; -1); (0; 4; -1);  (5; 0; 1) (5; 0; 1)
| №6 |  (5;3 ;-2 ); (5;3 ;-2 );  (0 ;4 ;6); (0 ;4 ;6);  (7 ;0 ;-1 ); (7 ;0 ;-1 );  (1;4 ;0 ) (1;4 ;0 )
|
| №7 |  (0; 3; -1); (0; 3; -1);  (5; 6; -1); (5; 6; -1);  (2; -1; 0); (2; -1; 0);  (1; 0; -1) (1; 0; -1)
| №8 |  (4;2 ;-3 ); (4;2 ;-3 );  (0 ;1 ;5 ); (0 ;1 ;5 );  (3 ;-1 ; 0); (3 ;-1 ; 0);  (6;0 ;-3 ) (6;0 ;-3 )
|
| №9 |  (1; 2; -5); (1; 2; -5);  (4; 3; 0); (4; 3; 0);  (3; 0; -2); (3; 0; -2);  (0; 2; -1) (0; 2; -1)
| №10 |  (3;0 ;-2 ); (3;0 ;-2 );  (5 ;-2 ;3 ); (5 ;-2 ;3 );  (4 ;-1 ;0 ); (4 ;-1 ;0 );  (0; 2; 1) (0; 2; 1)
|
| №11 |  (1; 2; 3); (1; 2; 3);  (0;4; 5); (0;4; 5);  (-3; -1; 0); (-3; -1; 0);  (2; 5; -1) (2; 5; -1)
| №12 |  (2; 4; 3); (2; 4; 3);  ( 1;0 ;-1 ); ( 1;0 ;-1 );  ( 2;2 ;-3 ); ( 2;2 ;-3 );  (0;7 ;-1 ) (0;7 ;-1 )
|
| №13 |  (3; 5; 0); (3; 5; 0);  (2; -1; 1); (2; -1; 1);  (0; 3; 4); (0; 3; 4);  (5; 2; 1) (5; 2; 1)
| №14 |  (-2;1 ;3 ); (-2;1 ;3 );  (4 ;2 ;3 ); (4 ;2 ;3 );  ( 3;-1 ;5 ); ( 3;-1 ;5 );  (1;0 ;2 ) (1;0 ;2 )
|
| №15 |  (6; 1; -1); (6; 1; -1);  (4; 0; 3); (4; 0; 3);  (2; 3; 0); (2; 3; 0);  (4; -1; 2) (4; -1; 2)
| №16 |  (1;0 ;-1 ); (1;0 ;-1 );  ( 5;-1 ;0 ); ( 5;-1 ;0 );  (3 ;2 ;1 ); (3 ;2 ;1 );  (0;-3 ;2 ) (0;-3 ;2 )
|
| №17 |  (5; 3; -4); (5; 3; -4);  (0; -1; 2); (0; -1; 2);  (1 ;2 ;0); (1 ;2 ;0);  (5; 6; -1) (5; 6; -1)
| №18 |  (6;0 ;3 ); (6;0 ;3 );  (3 ;-1 ;0 ); (3 ;-1 ;0 );  (5 ;1 ;2 ); (5 ;1 ;2 );  (4; 2 ;0 ) (4; 2 ;0 )
|
| №19 |  (1; -2; 5); (1; -2; 5);  (2 ;-1 ;1 ); (2 ;-1 ;1 );  (3 ;4 0); (3 ;4 0);  (0; 3; 1) (0; 3; 1)
| №20 |  (-1;2 ;0 ); (-1;2 ;0 );  (3 ;0 ;-2 ); (3 ;0 ;-2 );  (4 ;3 ;0 ); (4 ;3 ;0 );  (7; 2; -1) (7; 2; -1)
|
| №21 |  (3; 3; 0); (3; 3; 0);  (2; -1; 5); (2; -1; 5);  (0 ;4 ;-2 ); (0 ;4 ;-2 );  (1;-1 ; 3) (1;-1 ; 3)
| №22 |  (6; 0;-3 ); (6; 0;-3 );  (0 ;1 ;5 ); (0 ;1 ;5 );  (4; 2; 3); (4; 2; 3);  (2; 4; 0) (2; 4; 0)
|
| №23 |  (1; 0; 2); (1; 0; 2);  (3; -1; 5); (3; -1; 5);  (4 ;-2;3 ); (4 ;-2;3 );  (0; 2; -1) (0; 2; -1)
| №24 |  (0; 7;-1 ); (0; 7;-1 );  (2 ;2 ;3 ); (2 ;2 ;3 );  (1; 0; -1); (1; 0; -1);  (2; 4; -3) (2; 4; -3)
|
| №25 |  (5; 2; 1); (5; 2; 1);  ( 0; 3; 4); ( 0; 3; 4);  (2 ;-1 ;2 ); (2 ;-1 ;2 );  (3; 5; 0) (3; 5; 0)
| №26 |  (4;-3 ;5 ); (4;-3 ;5 );  (0 ;-1 ;2 ); (0 ;-1 ;2 );  (1 ;2 ;0 ); (1 ;2 ;0 );  (3;5 ;7 ) (3;5 ;7 )
|
| №27 |  (5;0; 1); (5;0; 1);  (0 ;4 ;-1 ); (0 ;4 ;-1 );  (3 ;-1 ;6 ); (3 ;-1 ;6 );  (1; 2; 0) (1; 2; 0)
| №28 |  (1;4 ;0 ); (1;4 ;0 );  ( 7;0 ;-1 ); ( 7;0 ;-1 );  (0 ;4 ;6 ); (0 ;4 ;6 );  (5;3 ;-2 ) (5;3 ;-2 )
|
| №29 |  (-1; 2; 0)№ (-1; 2; 0)№  (-2;0;3); (-2;0;3);  ( 0;3; 4); ( 0;3; 4);  (-5; 2; 7) (-5; 2; 7)
| №30 |  (2; 5;-1 ); (2; 5;-1 );  (-3 ;-1 ;0 ); (-3 ;-1 ;0 );  (0 ;2 ;3 ); (0 ;2 ;3 );  (4;0 ;-5 ) (4;0 ;-5 )
|
|
|
|
Задание 3.
Даны вершины треугольника 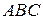 . Найти:
. Найти:
1) длину стороны 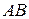 ;
;
2) уравнения сторон 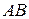 и
и 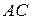 , их угловые коэффициенты;
, их угловые коэффициенты;
3) угол В в радианах;
4) уравнение высоты 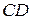 и ее длину;
и ее длину;
5) уравнение медианы  ;
;
6) координаты точки пересечения высоты 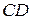 и медианы
и медианы  .
.
Варианты для самостоятельного решения.
| №1 | 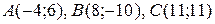
| №2 | 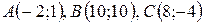
|
| №3 | 
| №4 | 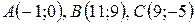
|
| №5 | 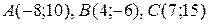
| №6 | 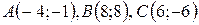
|
| №7 | 
| №8 | 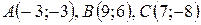
|
| №9 | 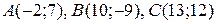
| №10 | 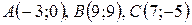
|
| №11 | 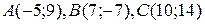
| №12 | 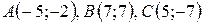
|
| №13 | 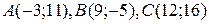
| №14 | 
|
| №15 | 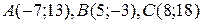
| №16 | 
|
| №17 | 
| №18 | 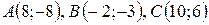
|
| №19 | 
| №20 | 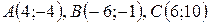
|
| №21 | 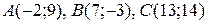
| №22 | 
|
| №23 | 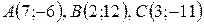
| №24 | 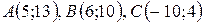
|
| №25 | 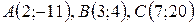
| №26 | 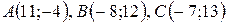
|
| №27 | 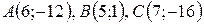
| №28 | 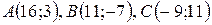
|
| №29 | 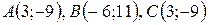
| №30 | 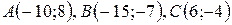
|
Задание 4.
Задачи класса «В». Дано уравнение линии второго порядка:
 .
.
Требуется:
1) привести общее уравнение линии второго порядка к каноническому виду;
|
|
|
2) исследовать, будут ли пересекаться эта линия и прямая 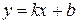 , если да, то найти координаты точек их пересечения;
, если да, то найти координаты точек их пересечения;
3) сделать чертеж.
Варианты для самостоятельного решения.
| №1 | 
| №2 | 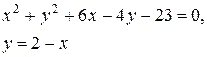
|
| №3 | 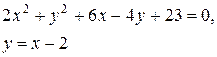
| №4 | 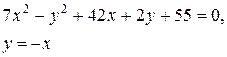
|
| №5 | 
| №6 | 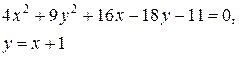
|
| №7 | 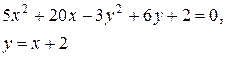
| №8 | 
|
| №9 | 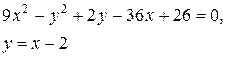
| №10 | 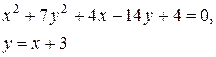
|
| №11 | 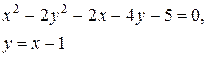
| №12 | 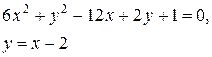
|
| №13 | 
| №14 | 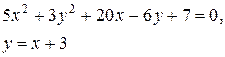
|
| №15 | 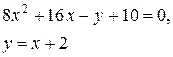
| №16 | 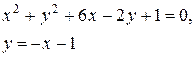
|
| №17 | 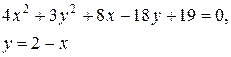
| №18 | 
|
| №19 | 
| №20 | 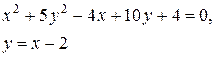
|
| №21 | 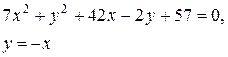
| №22 | 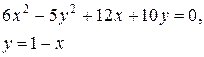
|
| №23 | 
| №24 | 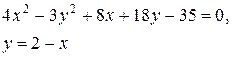
|
| №25 | 
| №26 | 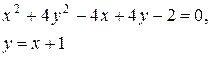
|
| №27 | 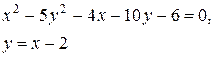
| №28 | 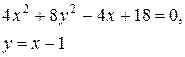
|
| №29 | 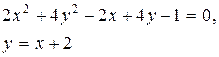
| №30 | 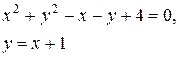
|
Задачи класса «А». Построить график квадратичной функции по основным точкам (точкам пересечения с осями координат, координатам вершины и направлениям ветвей).
Варианты для самостоятельного решения.
| № 1 | 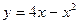
| № 2 | 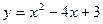
| № 3 | 
|
| № 4 | 
| № 5 | 
| № 6 | 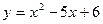
|
| № 7 | 
| № 8 | 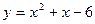
| № 9 | 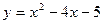
|
| № 10 | 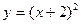
| № 11 | 
| № 12 | 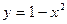
|
| № 13 | 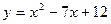
| № 14 | 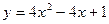
| № 15 | 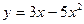
|
| № 16 | 
| № 17 | 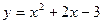
| № 18 | 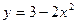
|
| № 19 | 
| № 20 | 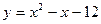
| № 21 | 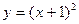
|
| № 22 |  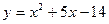
| № 23 | 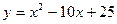 
| № 24 | 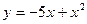
|
| № 25 | 
| № 26 | 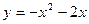 
| № 27 | 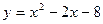
|
| № 28 | 
| № 29 | 
| № 30 | 
|
Задание 5.
Вычислить пределы функций. Номера примеров для задач класса «А»: 1, 2, 3, 4; задач класса «В»: 5, 6, 7, 8, 9.
Варианты для самостоятельного решения.
| №1 |  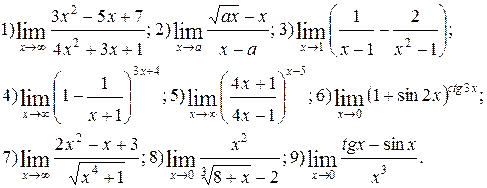
|
| №2 |  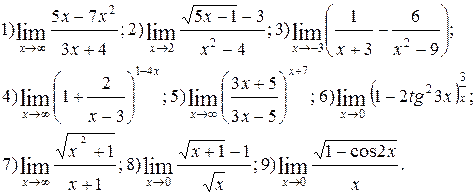
|
| №3 | 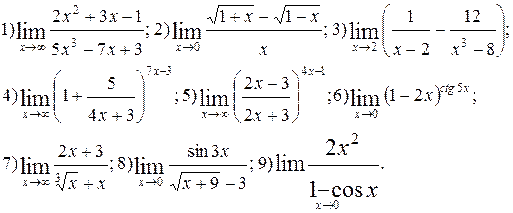
|
| №4 | 
|
| №5 | 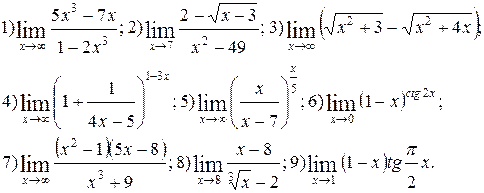
|
| №6 | 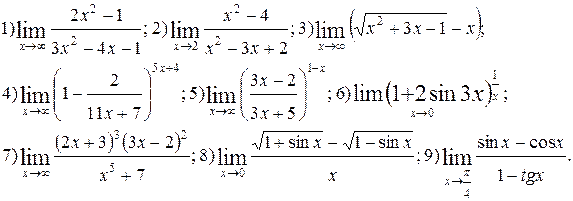
|
| №7 | 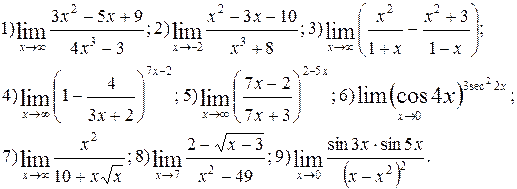
|
| №8 | 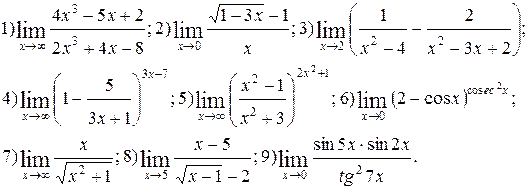 
|
| №9 | 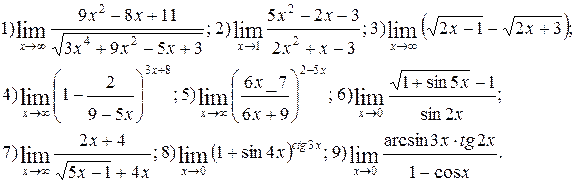
|
| № 10 | 
|
| № 11 | 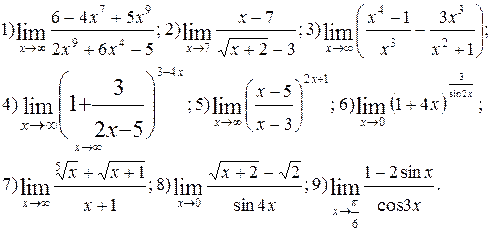
|
| № 12 | 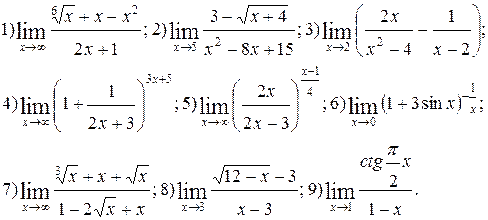
|
| № 13 | 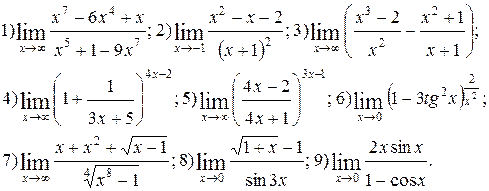
|
| № 14 | 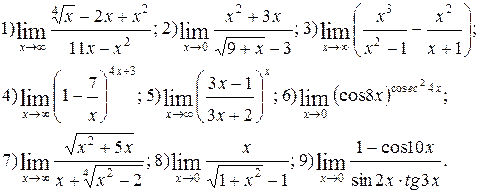
|
| № 15 | 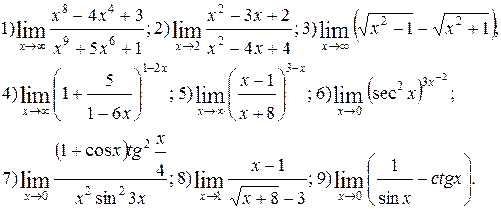
|
| № 16 | 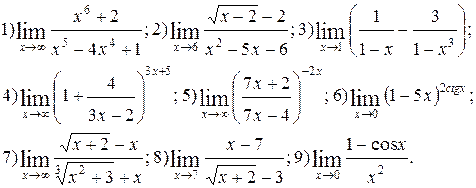
|
| № 17 | 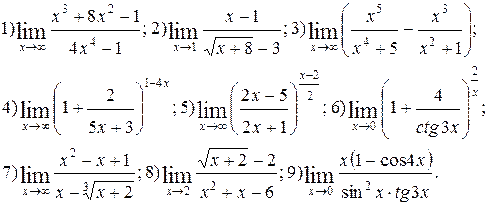
|
| № 18 | 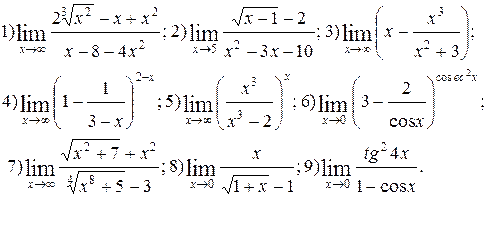
|
 №
19 №
19
| 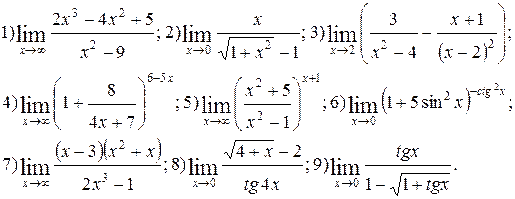
|
| № 20 | 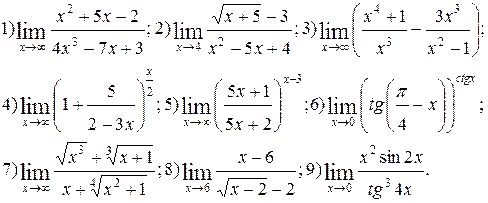 
|
| № 21 | 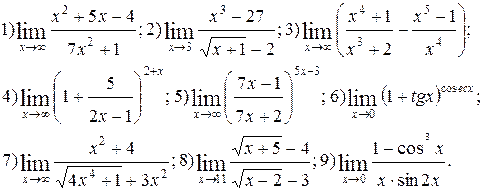 
|
| № 22 | 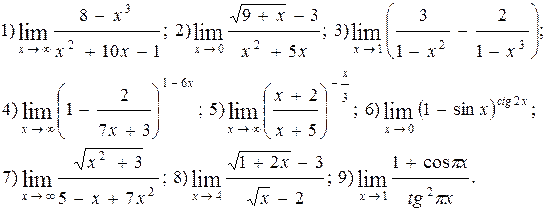
|
| № 23 | 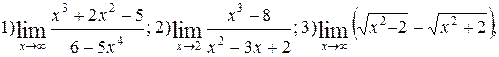

|
| № 24 | 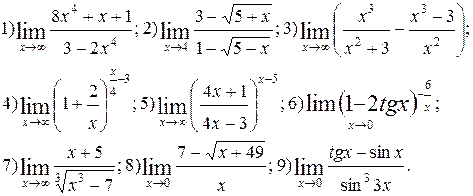
|
| № 25 | 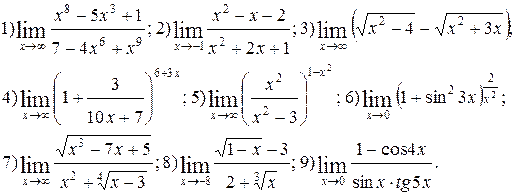
|
| № 26 | 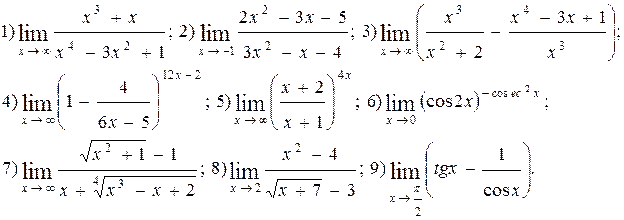
|
| № 27 |  
|
| № 28 | 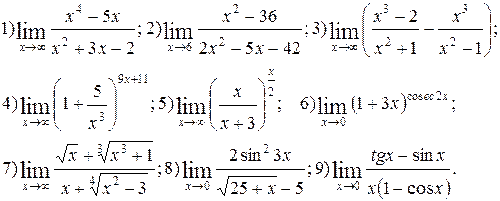
|
| № 29 | 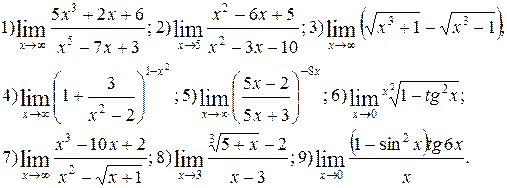
|
| № 30 | 
|
Задание 6.
Найти производные функций. Номера примеров задач класса «А»: 1, 2, 6, 7 и № 1 при нахождении производной второго порядка 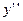 .
.
Варианты для самостоятельного решения.

| 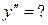
| |
| № 1 |
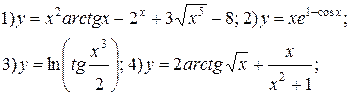
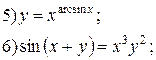 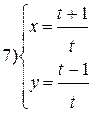
| 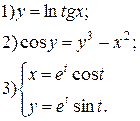
|
| № 2 |
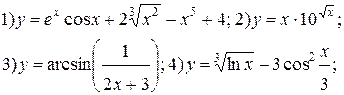
  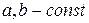  

| 
|
| № 3 | 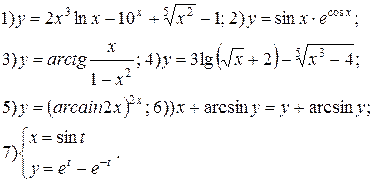
| 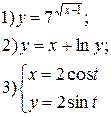
|
| № 4 | 
| 
|
| № 5 | 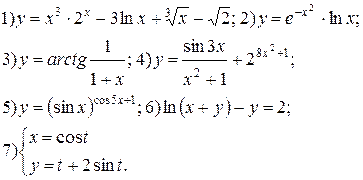
| 
|
| № 6 |
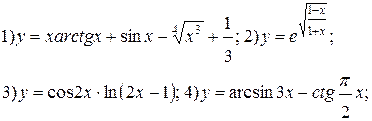
 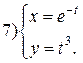
| 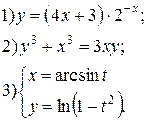
|
| № 7 |  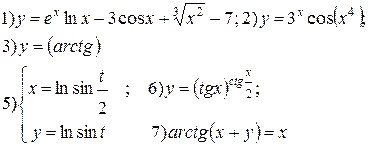
| 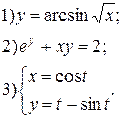
|
| № 8 |
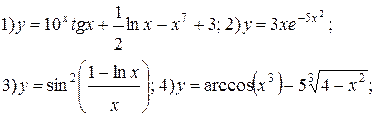
 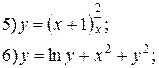 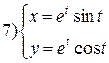
| 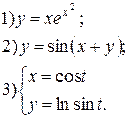
|
| № 9 |
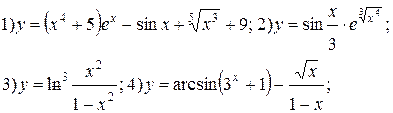 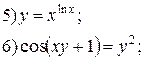 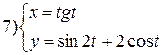
| 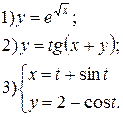
|
| № 10 | 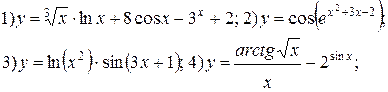 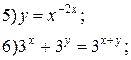 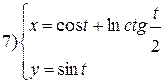
| 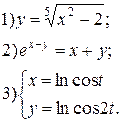
|
| № 11 |
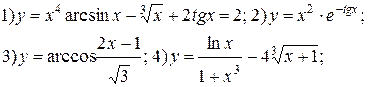
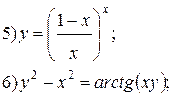 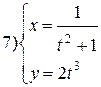
| 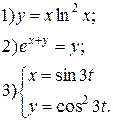
|
| № 12 | 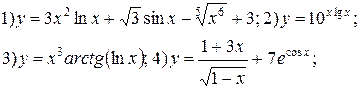
 
| 
|
| № 13 |  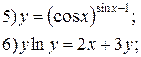 
| 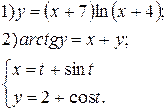
|
| № 14 | 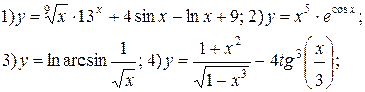
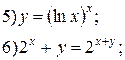 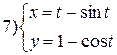
| 
|
| № 15 | 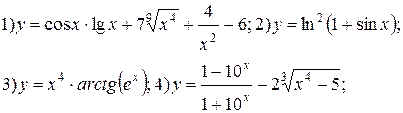
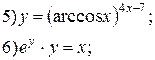 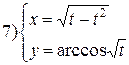
| 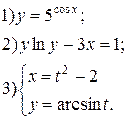
|
| № 16 | 
 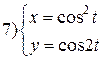
| 
|
| № 17 | 
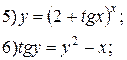 
| 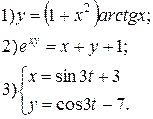
|
| № 18 |  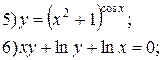 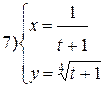
| 
|
| № 19 | 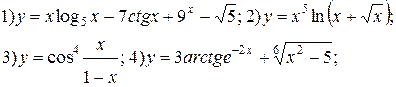
 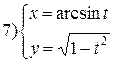
| 
|
| № 20 | 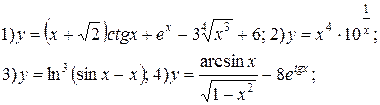
 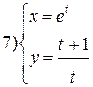
| 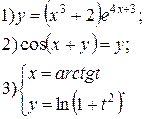
|
| № 21 | 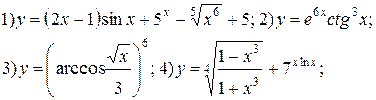
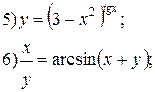 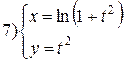
| 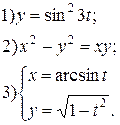
|
| № 22 | 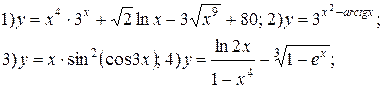
 
| 
|
| № 23 | 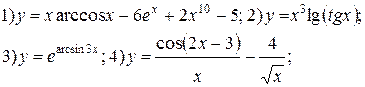
 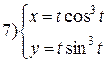
| 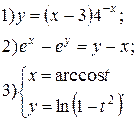
|
| № 24 | 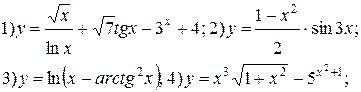
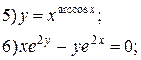 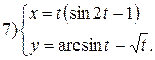
| 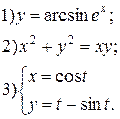
|
| № 25 | 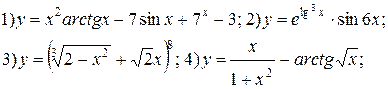
 
| 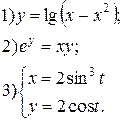
|
| № 26 |
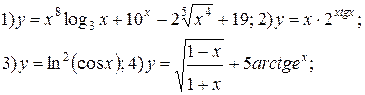
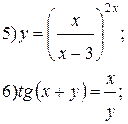 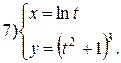
| 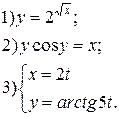
|
| № 27 | 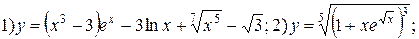
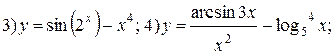
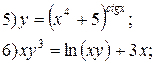 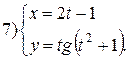
| 
|
| № 28 | 
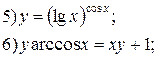 
| 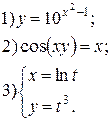
|
| № 29 | 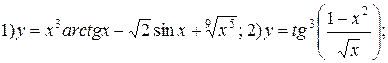

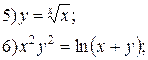 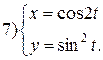
| 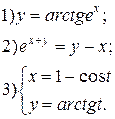
|
| № 30 | 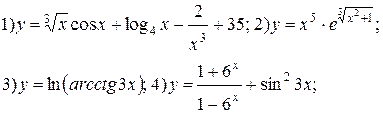
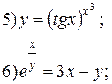  
| 
|
Задание 7.
Задача класса «В». Исследовать функцию и построить график.
Общая схема исследования функции и построения графика:
1) найти область определения функции и точки разрыва;
2) определить, является ли функция четной или нечетной, периодической;
3) найти точки пересечения графика с осями координат и интервалы знакопостоянства функции;
4) найти асимптоты функции;
5) найти точки экстремума и интервалы монотонности функции;
6) найти точки перегиба и интервалы выпуклости и вогнутости графика;
7) построить график функции, используя результаты исследования и, при необходимости, построение по точкам.
Варианты для самостоятельного решения.
| №1 | 
| №2 | 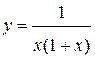
| №3 | 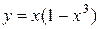
|
| №4 | 
| №5 | 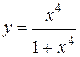
| №6 | 
|
| №7 | 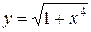
| №8 | 
| №9 | 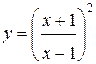
|
| №10 | 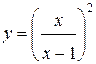
| №11 | 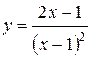
| №12 | 
|
| №13 | 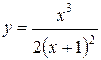
| №14 | 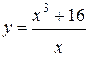
| №15 | 
|
| №16 | 
| №17 | 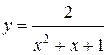
| №18 | 
|
| №19 | 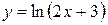
| №20 | 
| №21 | 
|
| №22 | 
| №23 | 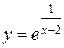
| №24 | 
|
| №25 | 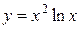
| №26 | 
| №27 | 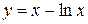
|
| №28 | 
| №29 | 
| №30 | 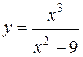
|
Задание 8.
Задача класса «А» . Найти наибольшее и наименьшее значения функции.
Общая схема исследования:
1) найти критические точки, лежащие внутри отрезка 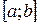 ;
;
2) вычислить значения функции на концах отрезка, то есть найти 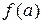 и
и 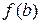 ;
;
3) сравнив найденные значения функции на концах отрезка со значениями функции в критических точках, выбрать наибольшее и наименьшее;
4) построить схематический график.
Варианты для самостоятельного решения.
| № 1 | 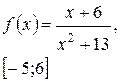
| № 2 | 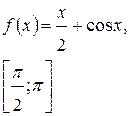
| № 3 | 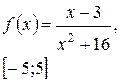
|
| № 4 | 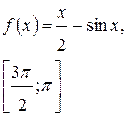
| № 5 | 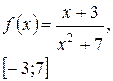
| № 6 | 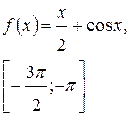
|
| № 7 | 
| № 8 | 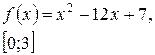
| № 9 | 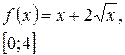
|
| № 10 | 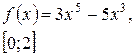
| № 11 | 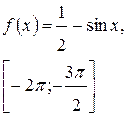
| № 12 | 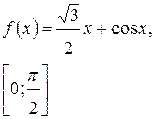
|
| № 13 | 
| № 14 | 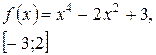
| № 15 | 
|
| № 16 | 
| № 17 | 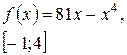
| № 18 | 
|
| № 19 | 
| № 20 | 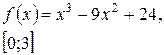
| № 21 | 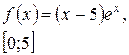
|
| № 22 | 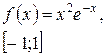
| № 23 | 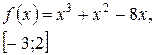
| № 24 | 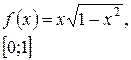
|
| № 25 | 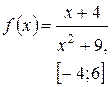
| № 26 | 
| № 27 | 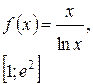
|
| № 28 | 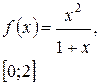
| № 29 | 
| № 30 | 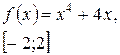
|
Образец выполнения семестровой расчетно-графической работы
Задание 1.
Решить данную систему по формулам Крамера, методом Гаусса и матричным способом
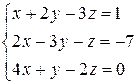 .
.
Решение.
1) Согласно формулам Крамера:

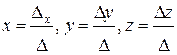 ,
,
найдем
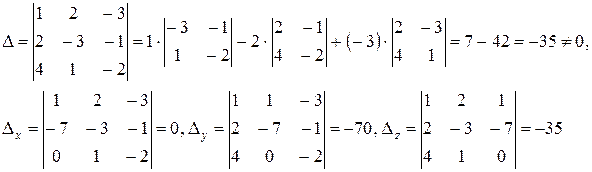
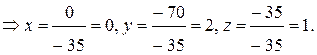
2) Проведем эквивалентные преобразования расширенной матрицы системы в соответствии с методом Гаусса:
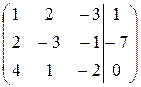
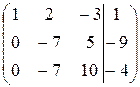


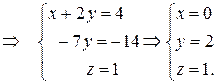
3) Определим матрицу, обратную матрице 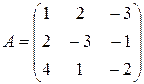 . Такая матрица существует, так как определитель матрицы А не равен нулю (
. Такая матрица существует, так как определитель матрицы А не равен нулю ( 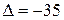 ). Найдем алгебраические дополнения
). Найдем алгебраические дополнения
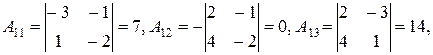

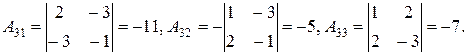
 Теперь транспонируем матрицу, составленную из алгебраических дополнений, и разделим ее элементы на
Теперь транспонируем матрицу, составленную из алгебраических дополнений, и разделим ее элементы на  , тогда обратная матрица
, тогда обратная матрица
 .
.
Вектор решений системы получим, умножив полученную обратную матрицу  на вектор-столбец свободных членов:
на вектор-столбец свободных членов:
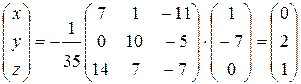 .
.
Таким образом, всеми тремя способами получено решение: 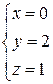 .
.
Задание 2.
Даны вершины треугольной пирамиды:  (2;-3;1),
(2;-3;1),  (6;1;-1),
(6;1;-1),  (4;8;-9) и
(4;8;-9) и  (2;-1;2).
(2;-1;2).
Требуется найти:
1) длину ребра 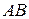 ;
;
2) площадь грани 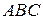 ;
; 
3) угол между ребрами  и
и 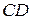 ;
;
4) объем пирамиды 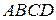 ;
;
5) уравнение плоскости АВС;
6) уравнения высоты, опущенной из вершины  на грань
на грань 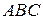 ;
;
7) уравнения стороны 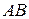 ;
;
8) длину высоты, опущенной из вершины  на грань
на грань 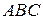 .
.
Решение.
1) Длина ребра 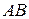 определяется по формуле:
определяется по формуле:

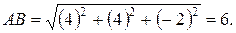
2) Площадь грани 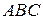 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 
 и
и 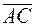 . Так как
. Так как
 ,
, 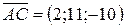 , то
, то
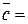
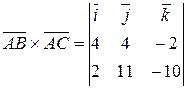
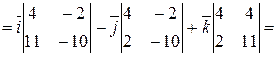
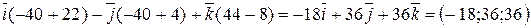 , то площадь треугольника
, то площадь треугольника 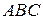 определяется по формуле
определяется по формуле
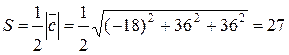 .
.
3) Косинус угла 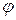 между ребрами
между ребрами  и
и 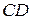 определяется по формуле
определяется по формуле 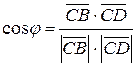 . Найдем
. Найдем  и
и 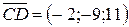 , тогда
, тогда
 рад.
рад.
4) Объем пирамиды находим, используя формулу 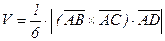 , определив предварительно
, определив предварительно

 5) Найдем уравнение плоскости
5) Найдем уравнение плоскости 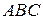 , используя уравнение плоскости, проходящей через три точки:
, используя уравнение плоскости, проходящей через три точки:
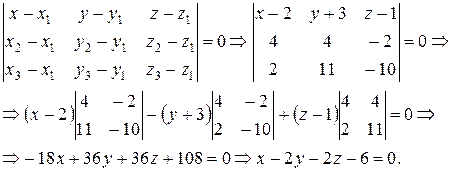
6) Канонические уравнения прямой, проходящей через данную точку  параллельно вектору
параллельно вектору  , имеют вид
, имеют вид
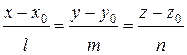 .
.
В данном случае 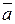 совпадает с нормалью
совпадает с нормалью  , проведенной к плоскости грани
, проведенной к плоскости грани 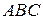 , поэтому искомые уравнения имеют вид
, поэтому искомые уравнения имеют вид
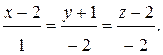
7) Чтобы записать уравнения стороны 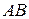 , используем уравнения прямой, проходящей через две точки:
, используем уравнения прямой, проходящей через две точки:
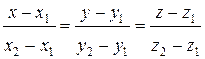 , тогда получим:
, тогда получим:
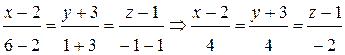 .
.
8) Найдем длину высоты, опущенной из вершины  на грань
на грань 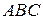 , согласно формуле
, согласно формуле

Задание № 3
Даны вершины треугольника: 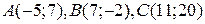 . Найти:
. Найти:
1) длину стороны 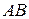 ;
;
2) уравнения сторон 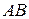 и
и 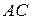 и их угловые коэффициенты;
и их угловые коэффициенты;
3) угол В в радианах;
4) уравнение высоты 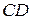 и ее длину;
и ее длину;
5) уравнение медианы  ;
;
6) координаты точки пересечения высоты 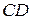 и медианы
и медианы  .
.
Решение.
1) Найдем длину стороны 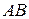 по формуле
по формуле

2) Уравнение прямой, проходящей через две точки имеет вид 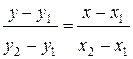 .
.
Тогда уравнение стороны 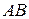 :
:
 ,
,
а угловой коэффициент 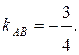
Аналогично, уравнение стороны  :
:

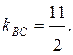
3) Внутренний угол В заметается вращением стороны ВС против часовой стрелки до совпадения с АВ, поэтому, используя формулу 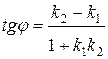 , надо в ней считать за первую прямую ― ВС, а за вторую ― АВ. Тогда
, надо в ней считать за первую прямую ― ВС, а за вторую ― АВ. Тогда 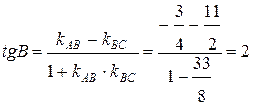
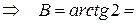 1,11.
1,11.
4) Отметив, что угловые коэффициенты 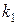 и
и  перпендикулярных прямых связаны зависимостью
перпендикулярных прямых связаны зависимостью 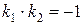 , т.е.
, т.е.  , используем уравнение пучка прямых, проходящих через данную точку
, используем уравнение пучка прямых, проходящих через данную точку  :
: 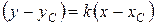 . Отсюда уравнение высоты
. Отсюда уравнение высоты 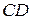 имеет вид
имеет вид
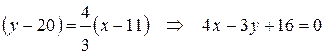 .
.
Расстояние от точки 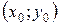 до прямой
до прямой 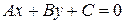 можно определить по формуле
можно определить по формуле 
5) Найдем координаты точки 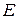 - середины отрезка
- середины отрезка  :
:
 .
.
Используя уравнение прямой, проходящей через две точки, получим уравнение медианы  :
:
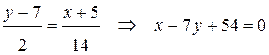 .
.
6) Точку  пересечения высоты
пересечения высоты 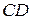 и медианы
и медианы  , находим, решив систему уравнений,
, находим, решив систему уравнений,
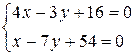
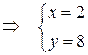

Задание № 4 (класс «В»)
Дано уравнение линии второго порядка:  .
.
Требуется:
1) привести общее уравнение линии второго порядка к каноническому виду;
2) исследовать, будут ли пересекаться эта линия и прямая 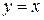 , если да, то найти координаты точки их пересечения;
, если да, то найти координаты точки их пересечения;
3) сделать чертеж.
Решение.
1) Преобразуем заданное уравнение к виду
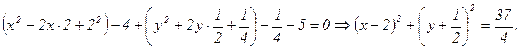
Получили уравнение окружности с центром в точке 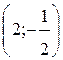 и радиусом
и радиусом 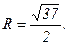
2) Подставим значение 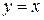 в заданное уравнение. Получим уравнение
в заданное уравнение. Получим уравнение
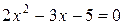 , корни которого
, корни которого  . Соответствующие значения
. Соответствующие значения 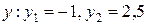 .
.
Таким образом, получили две точки пересечения заданных окружности и прямой: 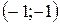 и
и  .
.
3) Точки пересечения окружности с осью о y найдем, решив систему:
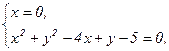 получим
получим 
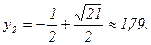 Решив систему
Решив систему  найдем точки пересечения с осью о x:
найдем точки пересечения с осью о x:  . Строим окружность с центром в точке
. Строим окружность с центром в точке 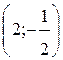 , радиусом
, радиусом 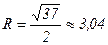 и прямую
и прямую 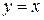 .
.

Задание № 4 (класс «А»)
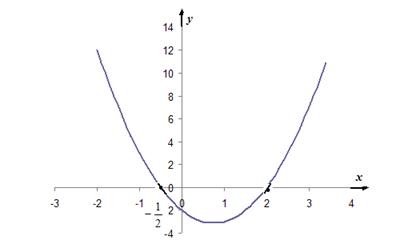
Исследовать квадратичную функцию 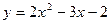 и построить ее график.
и построить ее график.
Решение.
Выписываем коэффициенты: а=2, в=-3, с=-2. Так как а=2>0, то ветви параболы направлены вверх.
Находим координаты вершины 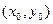 .
.
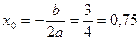 ;
;  .
.
Находим точки пересечения с осями координат. С осью о x при  , решая уравнение
, решая уравнение 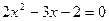 , находим 2 корня:
, находим 2 корня:  ,
,
С осью о y при x =0: y =-2.
Задание № 5
Вычислить пределы функций.
Решение.
1) 
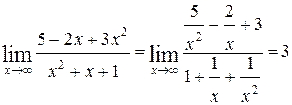 .
.
2)  .
.
3) 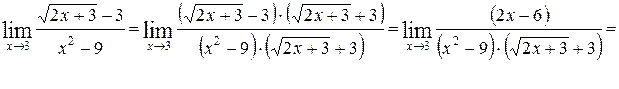
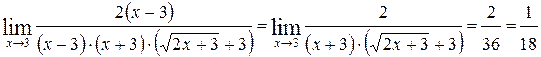 .
.
4) 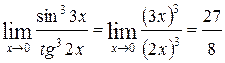 .
.
При решении использовали первый специальный предел  и теоремы о применении эквивалентных бесконечно малых в пределах.
и теоремы о применении эквивалентных бесконечно малых в пределах.
5) 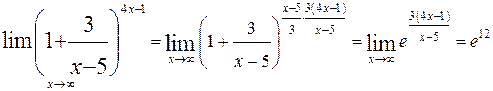 .
.
При решении использовали второй специальный предел, а также 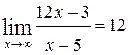 .
.
6)  .
.
При решении использовали второй специальный предел, предварительно сделав замену
 . Отметим, что условию
. Отметим, что условию 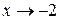 соответствует
соответствует  .
.
7) 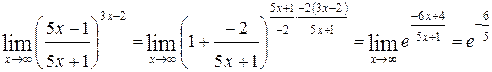 .
.
Задача решается аналогично задаче 5.
8) 

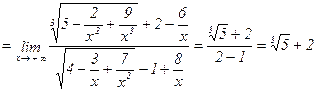 .
.
9) 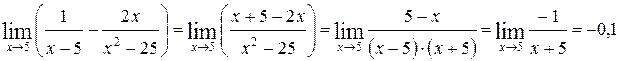
Задание № 6.
Найти производные.
Решение.
1)
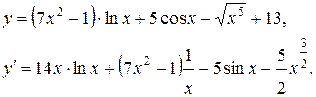
2) 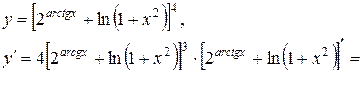

3) 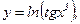
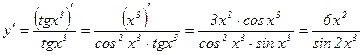
4)

5) 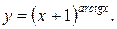
Предварительно прологарифмируем по основанию e обе части равенства:
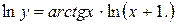
Теперь продифференцируем обе части, считая  сложной функцией от переменной
сложной функцией от переменной 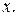 Тогда
Тогда
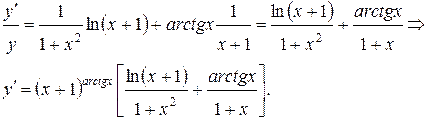
6) 
В данном случае функция 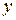 задана неявно. Чтобы найти производную следует продифференцировать по
задана неявно. Чтобы найти производную следует продифференцировать по 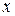 обе части заданного уравнения, считая при этом
обе части заданного уравнения, считая при этом 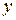 функцией
функцией 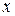 , а затем полученное уравнение разрешить относительно искомой производной
, а затем полученное уравнение разрешить относительно искомой производной 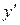 .
.
Имеем:
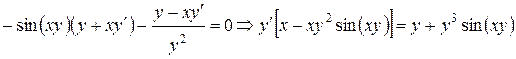 ,
,
откуда
 .
.
7) 
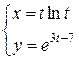
Зависимость между переменными 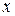 и
и 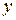 задана параметрическими уравнениями. Искомая производная определяется по формуле
задана параметрическими уравнениями. Искомая производная определяется по формуле 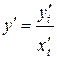 .
.
Имеем:
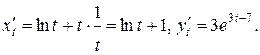
Откуда 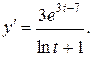
2. Вычислим производные второго порядка:
1) 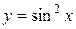 .
.
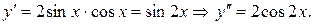
2) 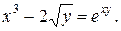
Продифференцируем обе части равенства по переменной 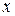 :
:
 .
.
Продифференцируем снова обе части первого полученного равенства по переменной 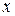 :
:
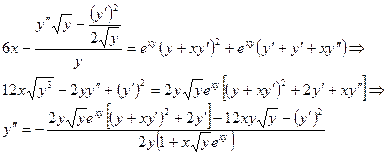
3) 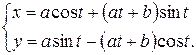
Величины 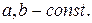
Зависимость между переменными 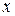 и
и 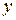 задана параметрическими уравнениями. Найдем сначала первую производную
задана параметрическими уравнениями. Найдем сначала первую производную 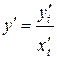 .
.
Имеем:

откуда
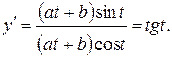
Тогда 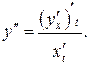
Используя 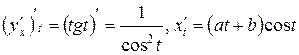 , получим
, получим

Задание № 7.
Задача 1. Исследовать функцию  и построить ее график.
и построить ее график.
Решение.
1. Область существования функции: 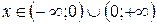 . Имеется единственная точка разрыва
. Имеется единственная точка разрыва 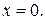
2. Функция не является ни четной, ни нечетной, так как 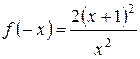 , поэтому условие четности
, поэтому условие четности  и условие нечетности
и условие нечетности 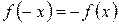 не выполняются. Функция непериодична.
не выполняются. Функция непериодична.
3. Найдем точки пересечения графика с координатными осями.
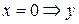 - не существует,
- не существует, 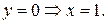

Найдем интервалы знакопостоянства функции. Очевидно, что функция всюду в области определения положительна.
4. Найдем асимптоты функции.
Вертикальной асимптотой будет прямая 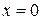 (ось ординат). Для определения наклонной асимптоты
(ось ординат). Для определения наклонной асимптоты 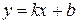 воспользуемся формулами
воспользуемся формулами

 Тогда
Тогда

Таким образом, асимптотой будет горизонтальная прямая 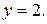
5. Найдем точки экстремума и интервалы монотонности функции. Находим первую производную:
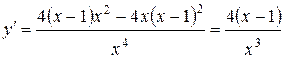
 .
.
Из условия 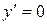 найдем
найдем 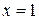 - стационарную точку. Построим таблицу
- стационарную точку. Построим таблицу
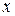
| 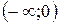
| 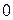
| 
| 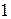
| 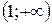
|
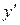
| + | - | 0 | + | |
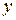
| возрастает | Не существует | Убывает | 0 | Возрастает |
Очевидно, что  .
.
6. Найдем точки перегиба графика функции и его интервалы выпуклости и вогнутости. Так как
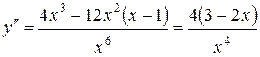 ,
, 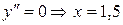 - абсцисса точки перегиба.
- абсцисса точки перегиба.
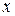
| 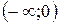
| 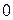
| 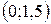
| 1,5 | 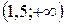
|
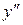
|  + +
| + | 0 | - | |
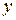
| 
| Не существует | 
| 
| 
|
7. Строим график функции
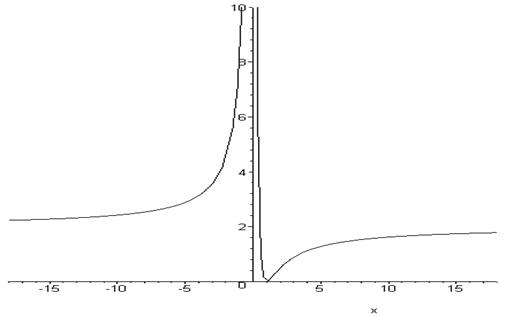
Задача 2. Исследовать функцию 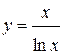 и построить ее график.
и построить ее график.
Решение.
1. Область существования функции 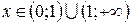 , так как
, так как 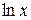 существует при положительных значениях
существует при положительных значениях 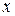 , а условию
, а условию  соответствует
соответствует 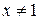 . Точка разрыва
. Точка разрыва 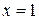 .
.
2. Функция не является ни четной ни нечетной, так как 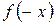 не определена. Функция непериодична.
не определена. Функция непериодична.
3. Точек пересечения функции с координатными осями нет. Интервалы знакопостоянства функции:
Функция положительна, когда 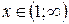 , и отрицательна, когда
, и отрицательна, когда 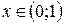 .
.
4. Найдем асимптоты:
1) Вертикальная асимптота: 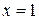 .
.
2) Наклонные асимптоты определяются по формуле 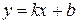 , где
, где  .
.
Тогда
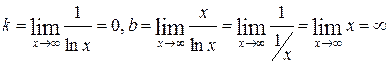 ,
,
причем последний предел определяют по формуле Лопиталя. Так как один из коэффициентов равен бесконечности, то наклонных асимптот функция не имеет.
5. Определим экстремумы функции и интервалы монотонности. Найдем сначала первую производную
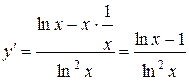 .
.
Критическую точку находим, решив уравнение  .
.
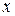
| 
| 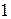
| 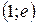
| 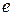
| 
|
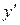
| - |  - -
| 0 | + | |
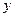
| убывает | Не существует | Убывает | 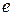
| Возрастает |
Функция имеет минимум в точке 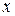 =
= 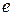 ,
, 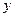 (
( 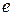 ) =
) = 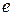 .
.
6. Найдем точки перегиба графика функции и его интервалы выпуклости и вогнутости. Так как  ,
,
 - абсцисса точки перегиба.
- абсцисса точки перегиба.
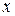
| 
| 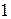
| 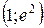
| 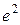
| 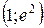
|
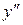
|  - -
| + | 0 | - | |
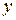
| 
| Не существует | 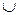
| 
| 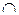
|
7. Построим график функции.
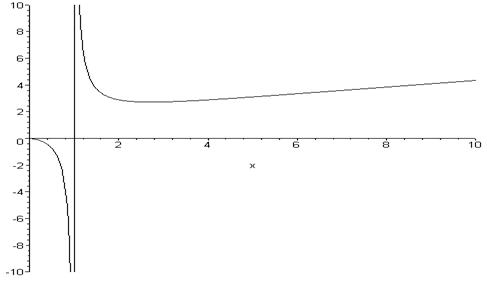
Задание № 8.
Найти наименьшее и наибольшее значения функции  на отрезке
на отрезке  .
.
Решение.
Найдем сначала критические точки, принадлежащие интервалу 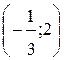 :
:
 .
.
Теперь вычислим значения заданной функции в критических точках и на концах отрезка:
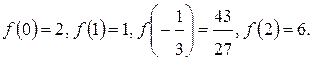
Сравнивая полученные значения функции, заключаем, что
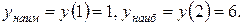
Библиографический список
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Том первый. М., 1964. 544 стр. с илл.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Том второй. М., 1978. 576 стр. с илл.
3. Берман Г.Н. Сборник задач по курсу математического анализа. М., 1975. 416 стр. с илл.
4. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс.- 3-е изд., испр. и доп. – М.: Айрис-пресс, 2003. – 576 с.: илл. – (Высшее образование).
Содержание
Задание 1…………………………………………………………………………………….….3
Задание 2………………………………………………………………………………………..4
Задание 3…………………………………………………………………………………...….. 5
Задание 4………………………………………………………………………………………..6
Задание 5………………………………………………………………………………………..7
Задание 6……………………………………………………………………………………....15
Задание 7……………………………………………………………………………………....22
Задание 8……………………………………………………………………………………....23
Образец выполнения семестровой расчетно-графической работы……………………......25
Библиографический список…………………………………………………………………..41
Дата добавления: 2021-01-20; просмотров: 205; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
